李 磊

(南開大學(xué)數(shù)學(xué)科學(xué)學(xué)院,300071,天津市)

0 引 言

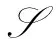
Ta,b(a)=Δ(a)以及Ta,b(b)=Δ(b),

對于無限維且可分的希爾伯特空間H來說,Semrl[19]證明了L(H) 是2-自同構(gòu)自反的;更進(jìn)一步的,對于一般的希爾伯特空間H,Ayupov 和 Kudaybergenow[2]證明了L(H) 是2-自同構(gòu)自反的. 另一方面,當(dāng)H是無限維可分的復(fù)希爾伯特空間時(shí),L(H) 是2-等距自反空間[13].

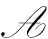
最近,本文作者及其合作者在文獻(xiàn)[11] 中考慮了弱拓?fù)湎碌?-局部等距算子,也即是定義了弱2-局部等距算子. 設(shè)E和F是巴拿赫空間,Δ 是從E到F的算子 (不要求線性,也不要求連續(xù)性). 如果對任意的x,y∈E和f∈y*,均存在從E到F的線性滿等距算子Tx,y,f(依賴于x,y和f) 使得

fΔ(x)=fTx,y,f(x),fΔ(y)=fTx,y,f(y),

則稱Δ是一個(gè)弱2-局部等距算子.

文獻(xiàn)[11] 用復(fù)分析的方法證明了球面 Kowalski-Sodkowski 定理. 由此研究了Lipschitz 函數(shù)空間上的弱2-局部等距算子的線性性.

對于向量值的函數(shù)空間,當(dāng)K是σ-緊度量空間且E是光滑自反巴拿赫空間 時(shí),Al-Halees 和 Fleming[1]證明了:C0(K,E) 是2-等距自反當(dāng)且僅當(dāng)E是2-等距自反的. Jiménez-Vargas等[8]人把此結(jié)果推廣到向量值 Lipschitz 函數(shù)空間上,他們證明了[8]:當(dāng)X和Y是緊度量空間且E是2-等距自反的光滑自反空間時(shí),從 Lip(X,E) 到 Lip(Y,E) 的2-局部等距算子Δ一定是滿線性算子,進(jìn)而可以寫成加權(quán)復(fù)合算子的形式. 最近,本文作者及其合作者研究了可微函數(shù)空間C(1)[0,1] 上的2-局部等距算子[10].

1 主要定理及其證明

‖x‖p:=(tr(x*x)p/2)1/p<∞

φx,y(x)=φ(x),φx,y(y)=φ(y).

tr(φ(x)φ(y)*)=tr(xy*).

因此,可以導(dǎo)出:對任意的有限秩算子x1,x2∈L(l2),都有

tr(φ(x1+x2)-φ(x1)-φ(x2))φ(y)*=tr((x1+x2)-x1-x2)y*=0,

進(jìn)而可知

tr(φ(x1+x2)-φ(x1)-φ(x2))(φ(x1+x2)-φ(x1)-φ(x2))*=0.

‖φ(x)-φ(y)‖p=‖x-y‖p.

值得注意的是,Molnár 在文獻(xiàn)[15] 中定義了另外一種2-局部等距算子.

定義1.2 設(shè)E和F是賦范空間,φ是從E到F的映射 (不要求線性). 如果對任意的x,y∈E,均存在從E到F的滿等距算子φx,y(不要求線性),使得

φ(x)=φx,y(x),φ(y)=φx,y(y).