Meng-Nan Chen(陳夢南) and Wen-Chao Chen(陳文潮)

1School of Science,Hangzhou Dianzi University,Hangzhou 310018,China

2Institute of Advanced Magnetic Materials,College of Materials and Environmental Engineering,Hangzhou Dianzi University,Hangzhou 310018,China

Keywords: Floquet theory,Weyl semimetal,topological phase transition,Hall conductivity

1. Introduction

In recent years,topological phases in periodically driven quantum systems have attracted a great surge of research interest. Based on the Floquet theory,such engineering has led to various theoretical proposals and experiments to produce Floquet topological insulators,Floquet topological superconductors,and Floquet Weyl semimetals(WSMs)in many contexts,such as the solid-state, atomic, and photonic systems.[1-27]The topology in these systems is defined in terms of the Floquet states,i.e.,the eigenstates of the single particle time evolution operator over one time period in the driven systems.The corresponding Floquet topological indices can therefore be defined in terms of the Floquet states,which are similar to their equilibrium analog.[3,28,29]The Floquet systems may also host unique topological phenomena without counterparts in static systems. For example,the discrete time crystal,which breaks continuous time translation symmetry and cannot exist in a static system.[30]

Much effort has been devoted to searching for Weyl fermions in three-dimensional (3D) materials both theoretically[31-36]and experimentally[37-41]recently because they exhibit a variety of interesting effects, including surface Fermi arc states and chiral magnetotransport. Weyl materials are usually manipulated by symmetry-breaking perturbations,such as the traditional application of strain, doping or static magnetic or electric fields. In contrast, Floquet engineering provides a more controllable way due to its high tunability.For noninteracting systems,the driving should be restricted to the off-resonant limit to prevent the system from being heated,with the frequency much larger than the energy scale of the system. Under this condition,the ground state for the system is still well-defined and an effective static Hamiltonian can be obtained,as clarified in the theoretical work of Kitagawaet al.for graphene and surface state of a 3D topological insulator,[42]where a topological phase transition from two-dimensional(2D)Dirac semimetal to quantum anomalous Hall(QAH)insulator was driven by light,which was in excellent agreement with later experiments.[4]This enables zero-temperature topological phases to exist in such nonequilibrium driving system.Therefore, we can use the standard quantum transport theory to deal with the spin and electron transport problems. The idea was soon extended to other 2D materials, including silicene and HgTe quantum well,[7,8]as well as 3D materials like Na3Bi[9]and nodal-line semimetals,[10-15]where both type-I and type-II WSMs can be realized and other various topological phases with interesting transport phenomena can emerge.The Floquet WSM phase with multi-Weyl nodes was also proposed in crossing nodal-line semimetals.[1,16,18]However,for interacting systems, off-resonant driving just postpones runaway heating for exponentially long time, where topological phases can not exist. Nandkishoreet al.[43]pointed out that many-body localized systems can avoid energy absorption from off-resonant driving by a local Hamiltonian, which ensures the occurrence of spontaneous breaking of the time continuous translation symmetry and leads to the discovery of discrete time crystal.[30,44]

In this paper,we demonstrate that a 3D topological insulator can be driven into a WSM by applying an off-resonant circularly polarized light, which acts effectively as a tunable Zeeman exchange field and an additional Dirac mass term.The Floquet Weyl nodes appear as critical points in the momentum space separating a QAH phase of the effective 2D system from an ordinary insulator phase,where the Dirac mass gap closes. We also study the anomalous Hall conductivities,including a disorder-averaged part which contains the contribution of electrons at the Fermi surface and an intrinsic part contributed by electrons below the Fermi surface. In the DC limit, the intrinsic Hall conductivity remains quantized when the Fermi energy is sufficiently close to the Weyl nodes. This approach is highly controllable by the intensity of light and provides an alternative method to realize the WSMs and QAH effects.

This paper is organized as follow. In Section 2,we introduce the model construction. The first Chern numbers for the system are derived,which reveals the topological nature of the system and determines the locations of the Weyl nodes in momentum space. In Section 3, we discuss the anomalous Hall conductivities inδ-correlated impurity potential.We conclude in Section 4.

2. Model construction and the first Chern number

Let us begin by considering the low-energyk·peffective Hamiltonian

We can find that the degrees ?τiand ?σihave totally been separated.

In the presence of circularly polarized light incident in thezdirection,the vector potential is given as

withE(t)=?A(t)/?t, whereη=+ (?) denotes the right(left) circularly polarized light andA0is the intensity of the light. By the Peierls substitution,k →k+eA(t), we obtain the full time-periodic HamiltonianHη(k,t).

In the Floquet picture,when the frequency of the light is sufficiently high, we can get a static effective Hamiltonian in the off-resonant approximation[42]

Fig.1. (a)The band dispersion when kx=ky=0 and(b)the first Chern numbers as functions of kz,where two subbands for κ =?touch at the Weyl nodes with nonzero first Chern number. The parameters are chosen to be M0=0.1,A1=0.7,A2=1.0,B1=2.5,B2=10, ?A0=0.1,and ω=20.Black dashed lines represent two different values for Fermi energies.

When the valance bands are fully filled and the conduction bands remain empty,there may exist an intrinsic quantum anomalous Hall conductivity, which is directly related to the first Chern number.[46]Whenkzis treated as a parameter,the Hamiltonian in Eq.(8)is equivalent to a 2D system,for which the first Chern number can be defined as

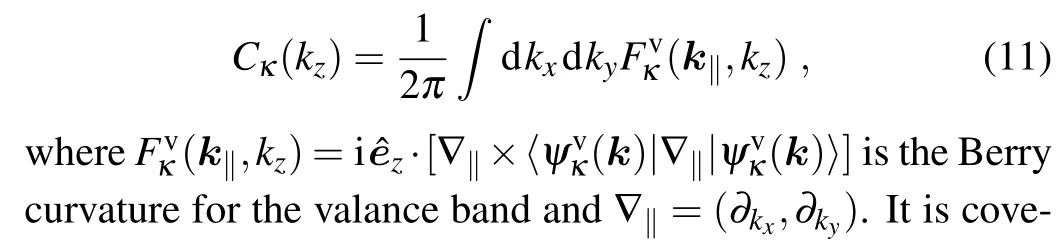
and it should be noted that only subbands forκ=?1 support the Weyl nodes. Then we expand theh?(k) to linear order ofkaround the Weyl nodes, followed by applying a rotation in thek‖plane and making some rescaling. This yields the standard Weyl Hamiltonian

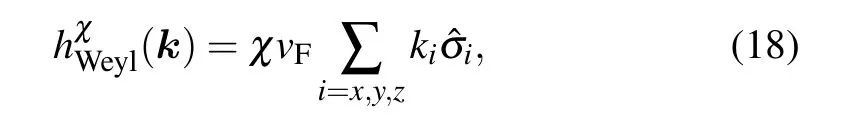
whereχ=±denotes the chirality of the two Weyl nodes andvFis the Fermi velocity,whose value is very close toA2since the band dispersion is linearized near the Weyl nodes, which is clearly illustrated in Fig.1. So in what follows,we will usevFto replaceA2for convenience.

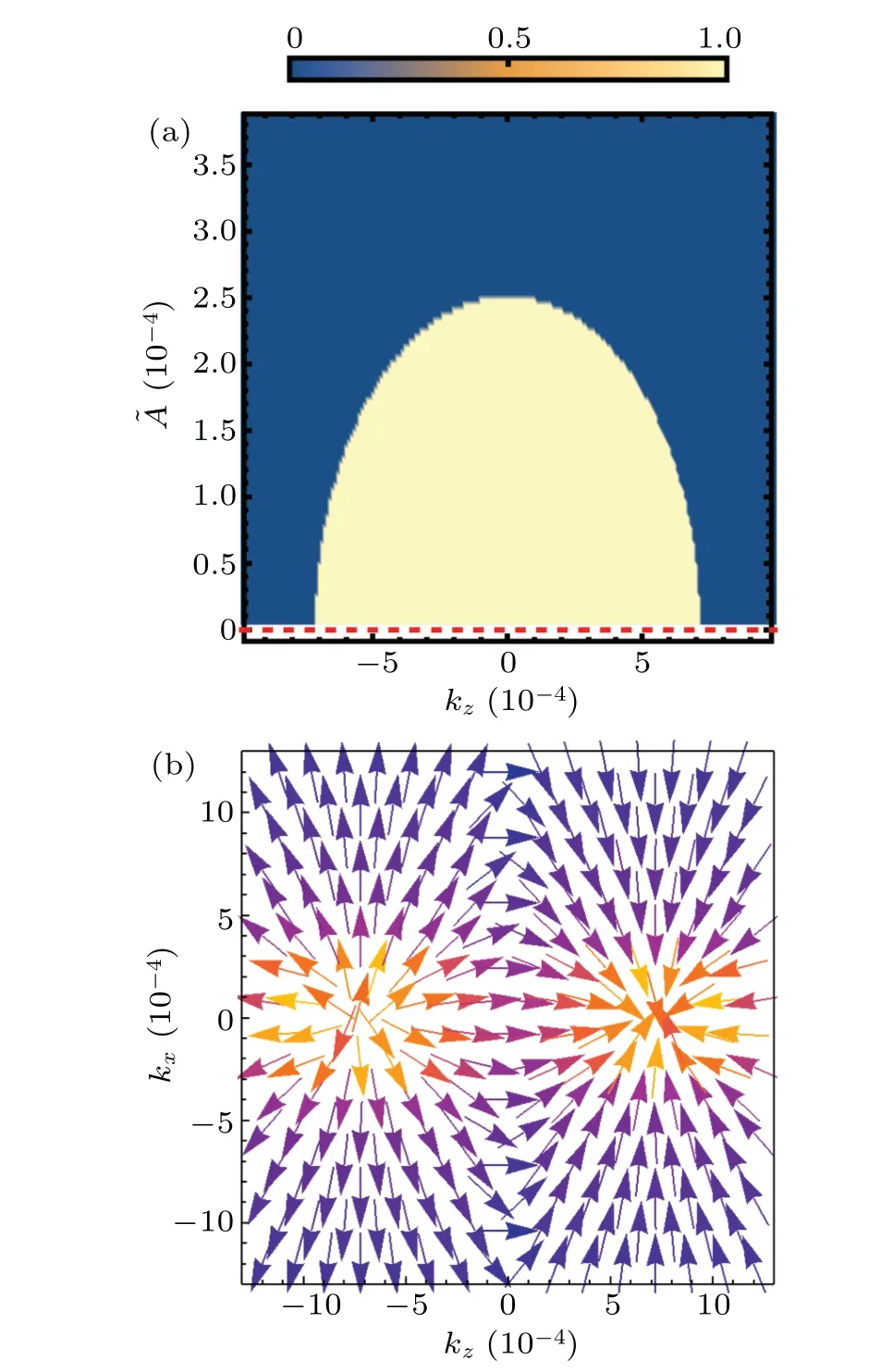
Fig.2. (a)Topological phase diagram determined from the first Chern numbers in the kz-?A plane,where ?A= ?A0 ?0.1 is the artificially shifted light intensity.The other parameters are the same as those in Fig.1.The red dashed line is used to label the value of ?A for which the distance between Weyl nodes in momentum space is the largest. (b)Field lines of the Berry curvature in the ky=0 plane.

3. The disorder averaged anomalous Hall conductivity

The discussions in the last section tell us that the main effect of an off-resonant circular polarized light is the generation of a time-reversal symmetry breaking perturbation. Therefore,the WSM phase and the anomalous Hall effect emerge naturally. In this section, we will explore the impurity-averaged anomalous Hall conductivity in the periodically driving system.

3.1. Impurity-averaged Hall conductivity at the Fermi surface

We consider the white-noise spin-independent random potential with zero mean value〈V(r)〉imp=0 and correlation function

Fig.3. (a)Feynman diagrams for the impurity averaged response function with the dressed vertex,in the presence of disorder(dashed lines).(b)The diffusion propagator with the ladder insertion.

Let us now find the explicit expression forΠI0x(q). Without loss of generality,qis taken asq=|q|?ey,due to the presence of full rotational symmetry inxyplane. We can rewrite Eq.(33)as

which represents the 0z-block of the diffusion propagator.Equation(27)allows us to approximate Eq.(38)asΓ(0)=0,which is known as the diffusion pole and agrees with the charge conservation Ward identity.[47,48]Combining Eqs.(36)and(37)and expandingΓ(Ω,0)to linear order ofΩ,we obtain the full expression forΠI0x(q)as

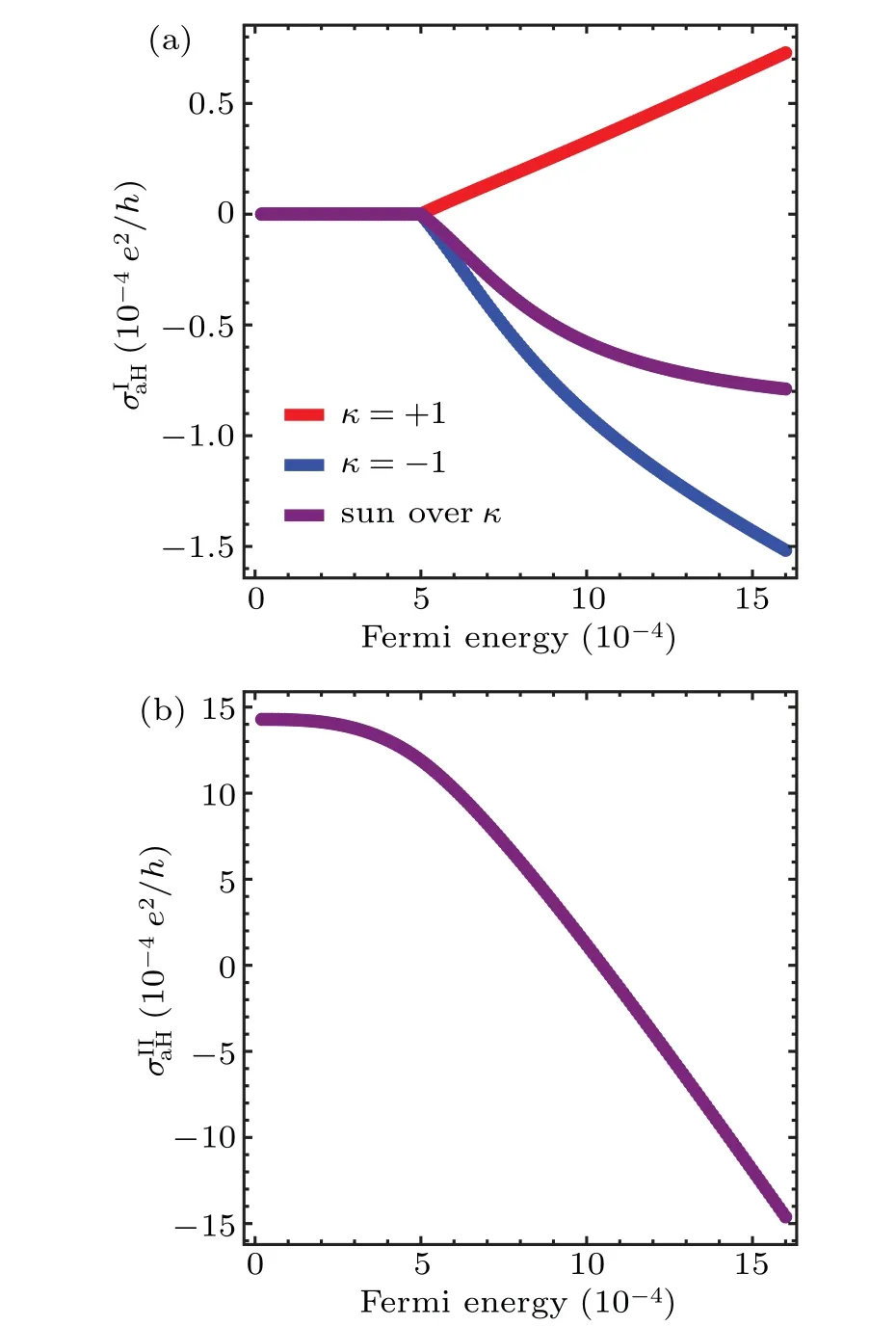
Fig.4. (a)The impurity-averaged Hall conductivity and(b)the intrinsic Hall conductivity as a function of the Fermi energy, where we set τκ0=1.

3.2. Intrinsic Hall conductivity below the Fermi surface

with

Therefore,theσaHdeviates from the quantized value slowly as shown in Fig.4(b),in which it can be found that if the Fermi energy is near the Weyl nodes,the Hall conductivity is not effected by the disorder significantly. While the Fermi energy is apart from the Weyl nodes, the behavior of the Hall conductivity is just like in normal metal phase.[47]For the case (ii),both of two sectorsκ=±1 contribute to the intrinsic Hall conductivity,leading a fast deviation from the quantized value,as Fig.4(b)shows.

4. Conclusion

We have analyzed the effects of an incident circular polarized light to a 3D topological insulator, we find that the topological phases and transport phenomena of the system can be tuned by varying the intensity of the light, under which the Weyl semimetal phase and anomalous Hall effect can emerge. Our proposal can be verified via the pump-probe angle-resolved photoemission spectroscopy (ARPES).[4,50,51]Our result provides a guidance for realizing Weyl materials and topological material engineering.