Ying-Jie Chen(陳英杰) and Feng-Lan Shao(邵鳳蘭)

School of Physics and Physical Engineering,Qufu Normal University,Qufu 273165,China

Keywords: Rashba spin-orbit interaction,quantum dot,polaron,temperature

1. Introduction

As nano science and technology grow rapidly, researchers are increasingly interested in investigations of lowdimensional quantum structures.[1-9]Recently,a great deal of interest has been drawn in studying spin-orbit interaction in semiconductor-based nanostructures.[10-12]One of the important and typical spin-orbit interaction in quantum dots(QDs)system is the Rashba spin-orbit interaction(RSOI)which was discovered by Rashba.[13]The RSOI originates structural inversion asymmetry of the confinement potential at heterointerface and plays a central role in spintronics.[14]In theory, many researchers have investigated the effect of RSOI on electromagnetism and optical properties of QDs in different ways. For example, Poszwa[15]studied spin states’quantum decoherence which was promoted by the RSOI due to an electron confined to a semiconductor QD in a magnetic field and used the second-order perturbation theory to solve the Schr¨odinger equation. Zhanget al.[16]investigated the thermoelectric effects revelent to the spin in an Aharonov-Bohm interferometer with four Rashba QDs coupled to two external one-dimensional semi-infinite metal leads theoretically. By use of the nonequilibrium Green function method,Yuanet al.[17]demonstrated the effect of mesoscopic Fano modulated by the RSOI and external magnetic field for the electronic transport in a mixed system consisting of a QD and an Aharonov-Bohm ring. The Rayleigh-Ritz variational method was adopted by Kumar[18]to research the ground state energy of aD0center under the RSOI in a GaAs QD system. Khordad[19]studied the susceptibility of QDs when all of the electron-electron interaction, RSOI and magnetic field affect it. In the process,he solved the Schr¨odinger equation to obtain the energy level and then gain the susceptibility using the canonical ensemble. Moreover, the experiments of lowdimensional semiconductor structures made great progress under the influence of the RSOI.Pueblaet al.[20]reported the evidence of optically stimulated spin-charge transition by Rashba spin-dependent splitting in the unoccupied state over the Fermi level at the Cu(111)/α-Bi2O3interface.Kogaet al.[21]demonstrated experimentally the electron spin inference phenomena based on the Rashba effect in quantum wells. Hofmannet al.[22]measured the spin-flip tunneling rates in double QDs based on GaAs by time resolution charge measurement and presented ways to tune the spin-flip tunneling rate. Their work not only provides a method for measuring the spin-orbit coefficients of Rashba and Dresselhaus but also made it feasible to turn on and off the effect of the spin-orbit interaction at a high on/off ratio. Meanwhile, researchers are recently interested in the thermodynamic properties of quantum dots because the thermodynamics properties of nanostructures are a fascinating subject in physics science.[23-31]For more information on this subject,please refer to Refs.[32-43]. Over recent years, applying the unitary transformation of Lee-Low-Pines type(UTLLPT)[44]and variational method of Pekar type(VMPT),[45,46]we have investigated some thermodynamic,electromagnetic and optical properties of QDs.[29-31,47-57]Although, in recent years, the Rashba effect[58-60]and magnetic field[61-63]influence of polaron in parabolic quantum dots have been studied,the temporal spatial distribution of the probability density (PD) and the influences of the RSOI and the temperature on the PD and the oscillating period (OP) of a parabolic QD (PQD) have not been accounted yet. In the present study,we mainly investigate the PD and OP in a PQD under the RSOI and temperature influences using the UTLLPT and VMPT.

The article is arranged as follows. In Section 2, we utilize the Hamiltonian to describe the system of a PQD under RSOI.Then,we focus our analysis on applying the UTLLPT and VMPT to infer the PD and OP of the polaron in the superposition state. In Section 3 we discuss the temporal spatial distribution of PD and the influences of RSOI and temperature on PD and OP of a PQD. Finally, conclusions are drawn in Section 4.

2. Theoretical model

In this study, based on the work reported in Refs. [48-50] and the interesting properties of electron spin in materials,[20-22]we concentrate on a polar crystal QD system in which an electron is bound by parabolic potential and magnetic field under RSOI.According to the theory of condensed matter, in polar materials, the negative and positive particles have reverse motion, which results in materials being polarized and interacting with electromagnetic field. These make the longitudinal optical (LO) phonon produced and cause a significant impact on their electrical and optical properties.We discuss the influence of RSOI on the properties of polaron in magnetic field and therein the influence of LO phonon is more important than that of acoustic phonon. The external magnetic field is along thezdirectionB=(0,0,B)and can be characterized with a vector potentialA=B(?y/2,x/2,0). Then the system’s Hamiltonian can be written in such a form

whereαis the electron-phonon coupling(EPC)strength.

When the structure of the system is unsymmetrical due to the size or morphology of the materials or an external electric field, the Rashba spin-orbit coupling will appear. In Eq. (1),the last item denotes the RSOI which is given by

2.1. Variational procedure

where|0〉phis the system zero phonon state and obeysaq|0〉ph= 0. Using the VMPT[45,46]and assuming that the Gauss function is still valid in the system and considering that the LO phonon has the electromagnetic properties, the trialwave functions of the ground and the first-excited state are selected as follows:

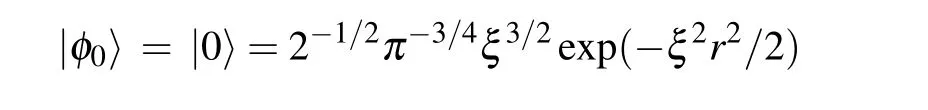
2.2. Probability density and oscillating period

On the basis of the quantum mechanical theories, the time-dependent quantum states of electrons may be expressed as

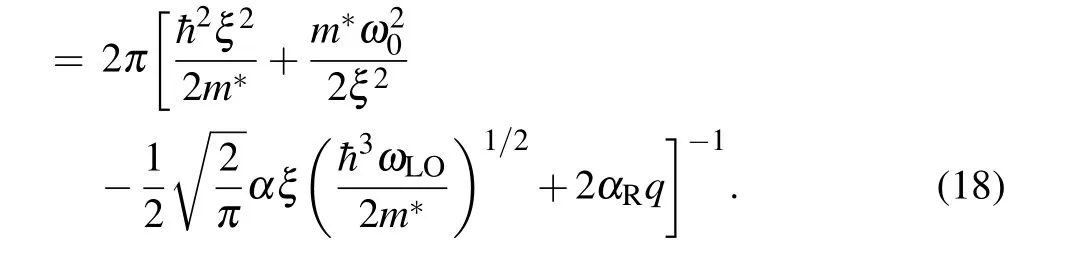
2.3. Temperature and RSOI influences

In this system, affected by the magnetic field and the RSOI potential,the average number of optical phonons of the superposition state around the electron in the QD is as follows:

Meanwhile,when the temperature is finite,the lattice vibration interacts with the electron in the QD system with the magnetic field and RSOI. The statistical mean of phonons in different states can describe the properties of polarons. According to the theory of quantum statistics, the mean of the bulk LO phonon can be obtained as follows:

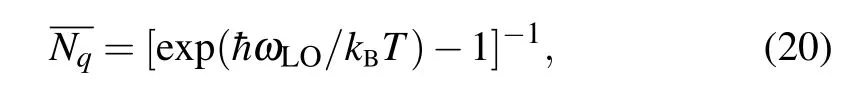
wherekBandTare the Boltzmann constant and temperature of the system.

Through self-consistent calculation of Eqs.(19)and(20),we can obtain the mean relationship with the variational parameterξand temperatureT. From Eqs. (14)-(20), we can obtain the relation ofQ,T0withξ,T,αR,ω0,αandq.

3. Results and discussion

Using the numerical calculus and derivation,the rules of the temporal spatial distribution of the PD at different temperatures and the relationships of the OP with the RSOI constant,confinement constant, EPC constant and phonon wave vector(PWV)under the RSOI in a PQD are gained. They are shown in Figs.1-5. In the process of characterization, we adopt the usual polaron units ˉh=2m*=ωLO=1.

Figure 1 displays that the polaron PDQ(r,t)in the superposition state of|0〉and|1〉changes with the time and coordinate under the RSOI in a PQD when the temperature is considered,settingω0=4,Rb=1,α=5,cosθ=1. The results reveal that the PD of the polaron has distinct spatial distribution at different times(its OP isT0=2π/ω01),and each time,space coordinate range has its corresponding amplitude of the PD whose value has a periodicity in the spacetime. Obviously,the PD has a minimum value att=0.5T0. These results show the law similar to that obtained by Liuet al.,[47]Chenet al.[57]and Fotueet al.[64]From Fig. 1, one can also obtain that the temperature does not lead to the periodicity of the PD with time and space to change,but the distributions of the PD at different temperatures are different. Those confirm that not only the presence of the polaron and difference observed is the amplitude of the probability density but also the temperature has an effect on its amplitude which is the result of temperature effects on the system state of the polaron. Such influence will not bring fundamental damage to the properties of the polaron in a certain temperature range,which is easy to understand because the temperature affects the motion of electrons and the vibration of lattice.

Fig.1. The PD Q(r,t,T)when the polaron is in the superposition state for(a)t=0T0,(b)t=0.25T0,(c)t=0.5T0,(d)t=0.75T0,(e)t=T0.

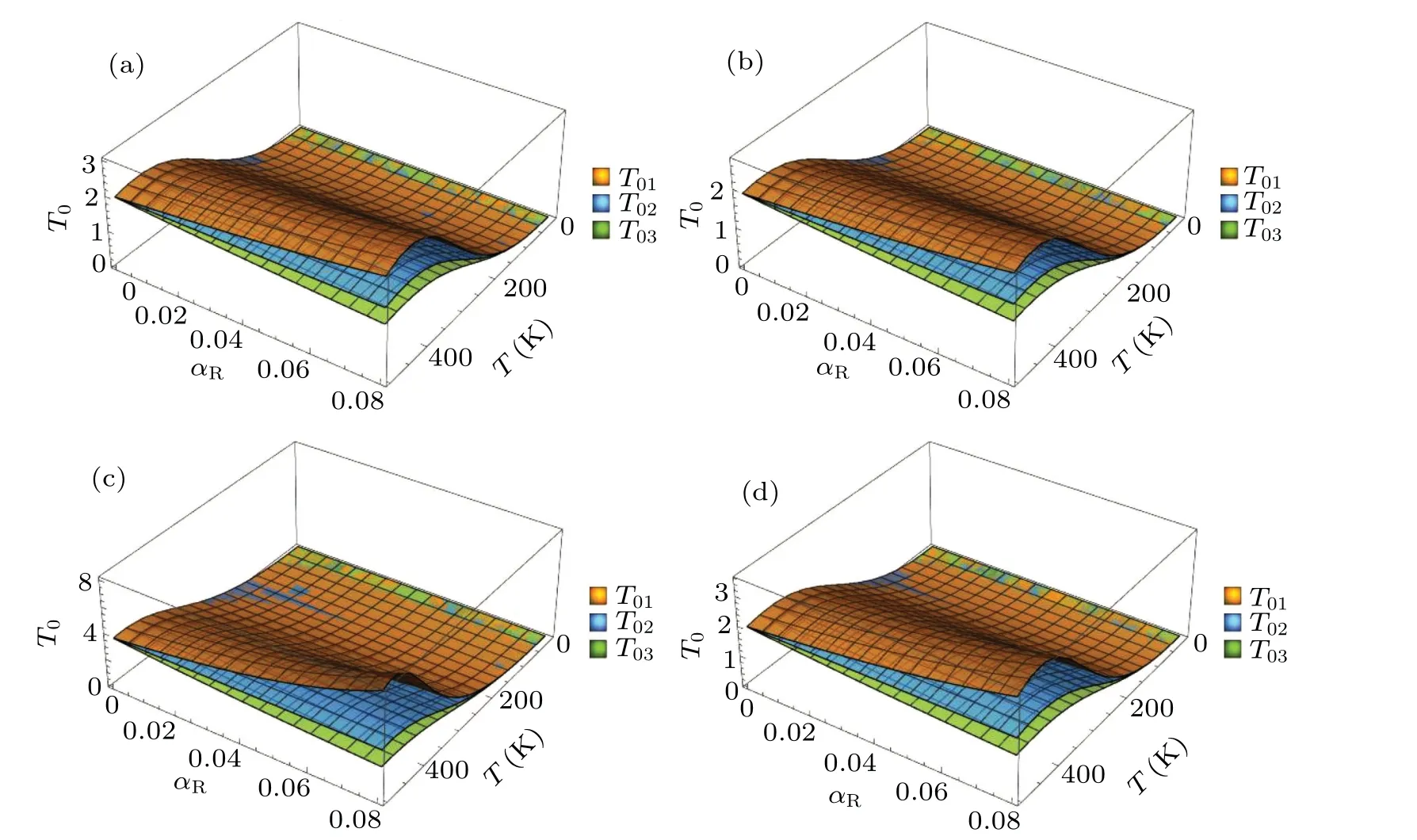
Fig.2. The OP as a function of the RSOI constant αR and the temperature T for(a)ω0=4.24,α =2,q=6,(b)ω0=4.47,α =2,q=6,(c)ω0=4.24,α =4,q=6,and(d)ω0=4.24,α =2,q=8.

Figure 2 describes the OP as a function of the RSOI constantαRand the temperatureTfor different confinement constantsω0, EPC strengthsαand PWVsq. The figure shows that the change laws ofT01andT03withαRare just opposite,that is, with the increase ofαR,T01increases whileT03decreases andT02does not vary, when the temperature is fixed.One can also see from them that the spacing of the OP between any two ofT01,T02andT03becomes larger with increasing the RSOI constant. This happens because the effects of the RSOI on the ground state energy and FESE are dissimilar and the influences of its intensity on them are also different. Under the effect of the RSOI,the excitation energy that is the difference between the FESE and the ground state energy is divided into three situations, meanwhile the OP is inversely proportional to the excitation energy. The properties of the ground excited state energy of the QD system have been widely studied experimentally and theoretically,[17,18,20,48-50]so that the OP has three cases and the spacing between any two of them becomes larger. The split of OP and the different effects on different branches caused by the RSOI are obviously consistent with the decoherence of the electronic state,[15]susceptibility of the electronic state[19]and splitting of the energy level[20]due to the electron spin. These testify each other. On the other hand,Fig.2 shows clearly that the OP will be very small at low temperature,which implies that low temperature has a destructive effect on electron and lattice vibrations. In addition,it can be seen from Fig. 2 that when the temperature reaches a higher value,the OP will fluctuate,which is the performance of high temperature destroying polaron state.

Fig.3. The OP as a function of the confinement constant ω0 and the temperature T for(a)αR =0.02, α =2, q=6, (b)αR =0.04, α =2,q=6,(c)αR=0.02,α =4,q=6,and(d)αR=0.02,α =2,q=8.

Fig. 4. The OP as a function of the EPC strength α and the temperature T for (a) αR =0.02, ω0 =4.24, q=6, (b) αR =0.04, ω0 =4.24,q=6,(c)αR=0.02,ω0=4.47,q=6,and(d)αR=0.02,ω0=4.24,q=8.

In addition,from Figs.3(a)-3(d),one can also see that the OP decreases when the confinement constant increases while it rises when the EPC strength grows in the presence of temperature. At the same time, one can find that the decreasing PWV makesT01larger andT03smaller. Such variation laws are shown more clearly in Figs.4 and 5. These results suggest that under the effect of the RSOI:(1)The growth of the confinement constant raises,which means that the bound coupling strength of the parabolic potential or the external magnetic field rises, the restriction on the electron thus shortening the time for the polaron to be in the superposition state and then the OP reduces.(2)Electrons may interact with more phonons with the strengthening of the coupling between the electron and the phonon,which will make more polarons in a superposition state and make the OP larger. (3) The PWV can affect the OP, which means that the motion velocity of the phonon can influence the OP of the polaron in the superposition state.The increase of wave vector accelerates the lattice vibration in a certain way,which makes more phonons and electrons interact with each other,thus increasing the lifetime of the polaron in the superposition state. (4)It is easy to understand that the temperature is a very important factor for the state of the polaron, which is the reaction of temperature to the motion of electron and the vibration of the lattice. Obviously,under different confinement constants and EPC strengthes and PWVs,the fluctuation amplitude of the OP varies with the temperature, but the variation law does not change. The reason is as analyzed in Fig.2.

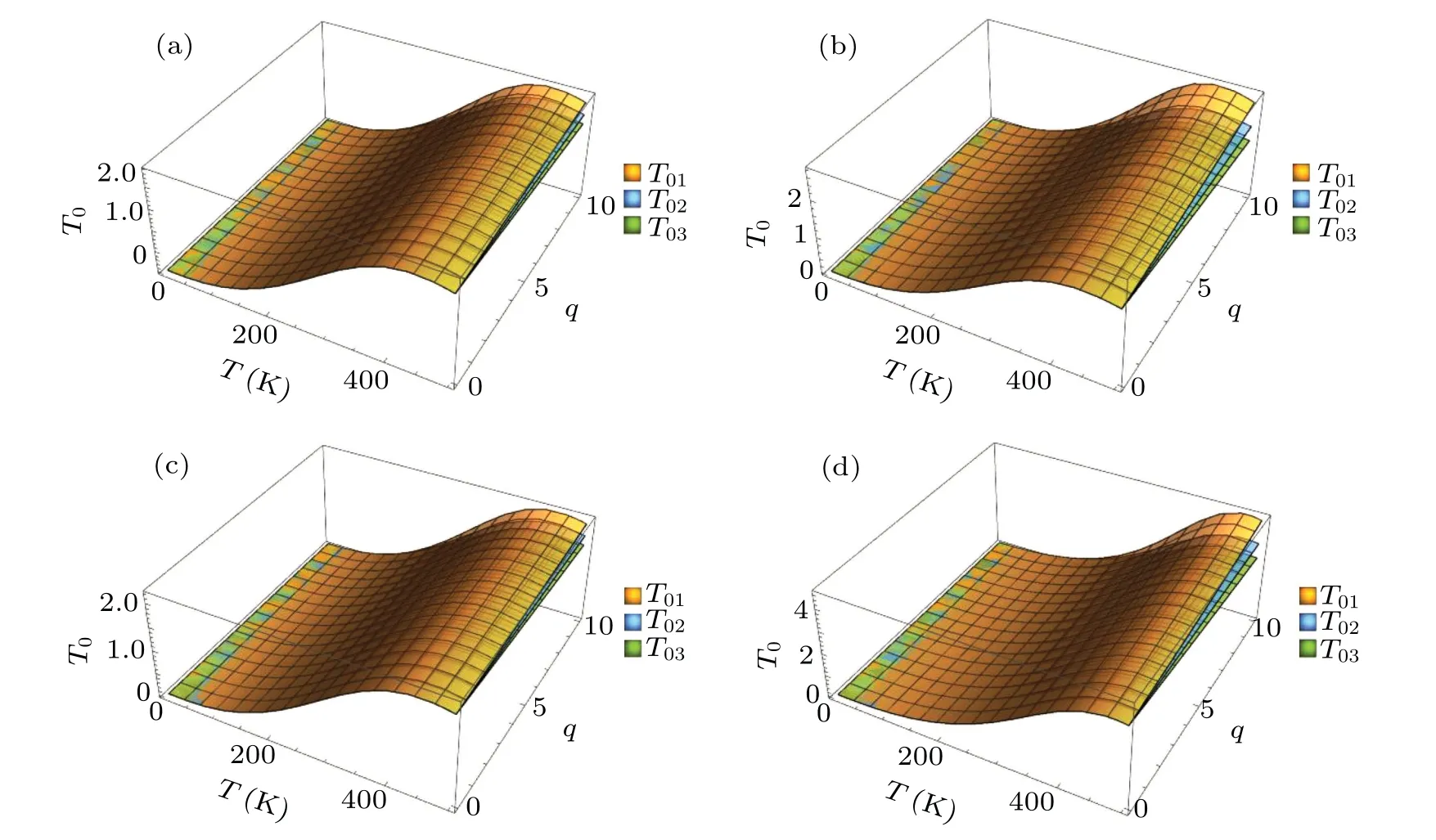
Fig.5. The OP as a function of the PWV q and the temperature T for(a)αR=0.02,ω0=4.24,α =2,(b)αR=0.04,ω0=4.24,α =2,(c)αR=0.02 ω0=4.47,α =2,and(d)αR=0.02,ω0=4.24,α =4.

Furthermore, Figs. 3-5 also reveal that the rule that the OP changes with one of the RSOI constant,confinement constant,EPC strength and PWV is not affected by the other three variables and the temperature.

4. Conclusions

Applying the unitary transformation of Lee-Low-Pines type and variational method of Pekar type, we have investigated the temporal spatial evolution of probability density of electrons and the influences of the Rashba spin-orbit interaction (RSOI) on the oscillating period of the polaron in a parabolic quantum dot with and without considering the temperature. Our results show that: (1)The temporal spatial distribution of the probability density is periodic. The amplitude of the periodic change is modulated by the temperature, but the temperature does not destroy the periodicity of the polaron state distribution. (2)As the RSOI’s presence, the oscillating period (OP) of the polaron is divided into different branches.(3)The effects of the electron-phonon coupling and the RSOI on the OP are positive, and the ones of the confinement constant are negative,and the ones of the phonon wave vector on its different branches are different. (4) The rule that the OP changes with one of four variables is not affected by the other three variables and the temperature. (5)The temperature plays a significant role in determining the properties of the polaron in a PQD.Only in a proper range of temperatures can the probability density and the OP have certain periodic changes and certain values.