Yuxia LIANG(梁玉霞)

School of Mathematical Sciences,Tianjin Normal University,Tianjin 300387,China

E-mail:liangyx1986@126.com

Abstract There is little work concerning the properties of quaternionic operators acting on slice regular function spaces de fined on quaternions.In this paper,we present an equivalent characterization for the boundedness of the product operator C?Dmacting on Bloch-type spaces of slice regular functions.After that,an equivalent estimation for its essential norm is established,which can imply several existing results on holomorphic spaces.

Key words essential norm;differentiation;composition operator;Bloch-type space;slice regular functions

1 Introduction

Gentili and Struppa first introduced slice hyperholomorphic functions in 2006(see,e.g.,[12]).Since then,many mathematicians have been involved in creating a theory regarding the functions of quaternionic variables,and this has several applications,for example in Schur analysis and operator theory.Associated with slice hyperholomorphic functions,there is a very rich literature on Schur analysis;see the book[1]and the references therein.Slice hyperholomorphic functions can also be referred to as slice regular,as they are de fined on quaternions and are quaternionic-valued.With the development of the theory of slice regular functions,there have appeared various slice regular function spaces,such as Fock space[2,11,26],Hardy and Bergman spaces[7,23],and Bloch,Besov and Dirichlet spaces[25]and so on.These quaternionic function spaces play important roles in quaternionic operator theory,which is different from the complex operator theory.As far as we are concerned,one of the main difference is the de finition of the spectrum of a linear operator,which is called the S-spectrum in quaternionic operator theory,and is widely used in fractional powers and fractional diffusion processes(see the excellent books[5,6]).

For a long time,describing the behavior of linear operators acting on various complex holomorphic function spaces has been a very fundamental topic.The linear operators include the(weighted differentiation)composition operators([4,17,19,20,24,27,28,30,31]),the integral-type operator([3])and so on.To the best of our knowledge,there is very little work on the properties of quaternionic operators on slice regular function spaces.Considering that the Bloch-type space is a convenient setting for many problems in functional analysis and the product operator C?Dmis a very general operator,we fix our attention in this paper on some classical and challenging problems to characterize the boundedness and compactness of this product operator acting between the Bloch-type spaces of slice regular functions.

We now recall some preliminaries regarding slice regular functions.For more information regarding the ensuing facts,we refer readers to[9,10].Let the symbol H denote the noncommutative,associative,real algebra of quaternions q=x0+x1e1+x2e2+x3e3=Req+Imq,with Req=x0and Imq=x1e1+x2e2+x3e3,where xjare real numbers for j=0,1,2,3,and the imaginary units e1,e2,e3are subject to the rule=?1.The set{e0=1,e1,e2,e3}is the usual basis of the quaternions.An element q∈H can also be written as a linear combination of two complex numbers,that is,q=(x0+x1e1)+(x2+x3e1)e2.Moreover,we can consider the space R3embedded in H as follows:

We say the conjugate of q∈H is q=Req?Imq and its modulus is|q|2==|Req|2+|Imq|2.Every q∈H can be expressed as q=x+yI,where x,y∈R and I=Imq/|Imq|if Imq0,otherwise we take I arbitrarily such that I2=?1.Let the symbol S denote the two-dimensional unit sphere of purely imaginary quaternions,meaning that

hence I∈S.It is obvious that q2=?1 for all q∈S.

In the sequel,we take i∈S and let C(i)denote the space generated by{1,i},which can be identi fied as the usual complex plane.It is easy to check that

The set B={q∈H:|q|<1}is a unit ball in H,and so Bi=B∩C(i)is identi fied as the unit disk D in the complex plane C(i)for i∈S.

We denote the space of holomorphic functions on D by H(D).For 0<α<∞,an f∈H(D)is said to be in the complex Bloch-type space or α-Bloch spaceif

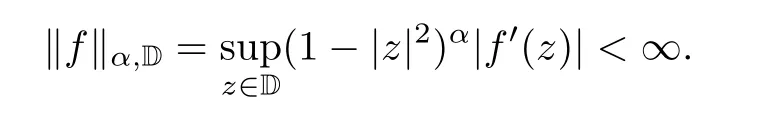
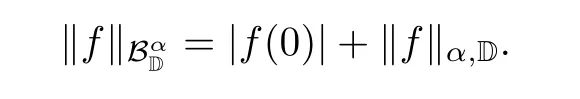
That the complex Bloch-type space is important in operator theory is due to its invariance with respect to M¨obius transformation.We refer the readers to the book[31]by Zhu,which is an excellent source concerning the development of theory on complex holomorphic function spaces.

As regards the theory of slice regular functions,it has been developed systematically in recent decades and is widely applied in quaternionic quantum mechanics;see e.g.,[10].Here we first present the de finition of slice regular functions and cite some basic properties;see,e.g.,[8,9,13].

De finition 1.1(Slice regular functions) Let ? be a domain in H.A real differentiable quaternionic-valued function f:?→H is called slice regular if,for any i∈S,its restriction fion ?i=?∩C(i)satis fies

for all x+yi∈?i.We denote by R(?)the set of all slice regular functions on ?.

Proposition 1.2(Splitting lemma) If f∈R(?),then for any i∈S and every j∈S orthogonal to i,there are two holomorphic functions F,G:?∩C(i)→C(i)such that,for any z=x+iy,it holds that

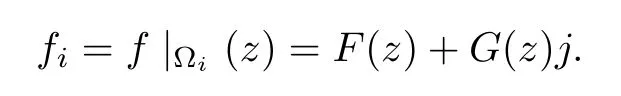
Slice regular functions possess good properties on speci fic open sets that we will call axially symmetric slice domains.On these domains,slice regular functions satisfy the representation formula,which allows us to reconstruct the values of the function once we know its values on some complex plane C(i).

De finition 1.3Let ??H be a domain.Then

(1)? is called a slice domain(or s-domain for short)if it intersects the real axis and if,for any i∈S,?iis a domain in C(i).

(2)? is called an axially symmetric domain if,for any x+yi∈? with x,y∈R and i∈S,the entire two-sphere x+yS is contained in ?.

Proposition 1.4(Representation Formula) Let f be a slice regular function on an axially symmetric s-domain ??H.Choose any j∈S.Then the following equality holds for all q=x+yi∈?:

Letting i,j∈S be mutually orthogonal vectors and ??H an axially symmetric s-domain,the splitting lemma and the representation formula entail the ensuing de finitions,which relate the slice regular function space R(?)on ? with the space of pairs of holomorphic functions on?i,denoted by H(?i).Afterwards,de fine

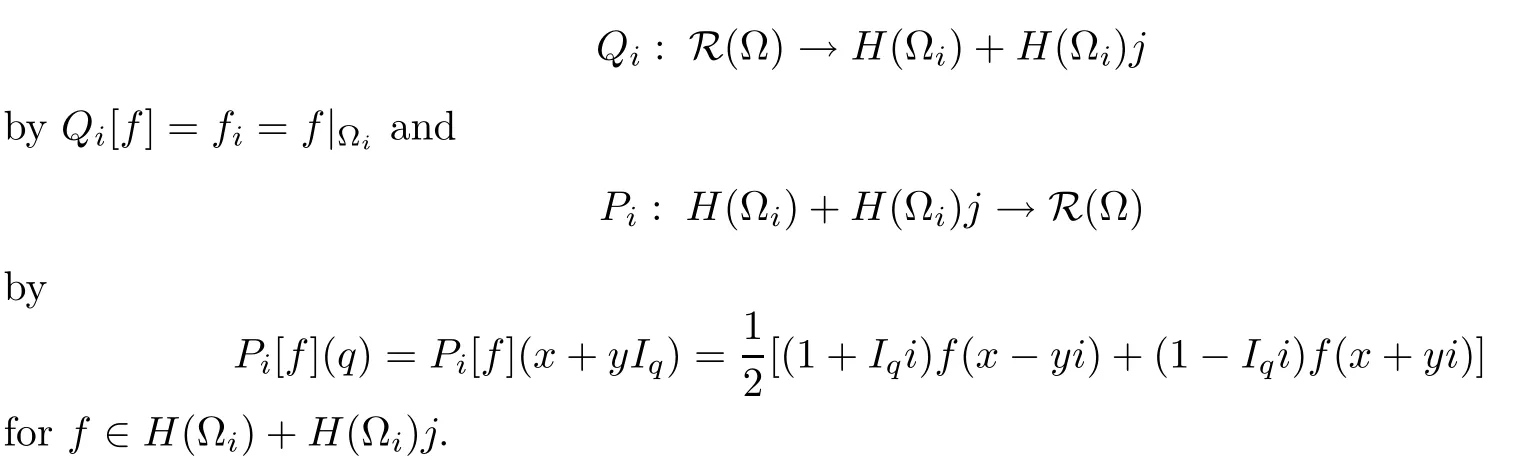
Based on the above mappings,we first recall a de finition for the slice regular α-Bloch space on the unit ball B from[15,De finition 2.1].Then we present its relation with a complex Bloch-type space.

De finition 1.5For 0<α<∞,the slice regular α-Bloch space associated with the unit ball B is the quaternionic right linear space of slice regular function f on B such that

where Re p=x0;that is to say,

It is easy to check that Bαis a Banach space endowed with the norm

where

is a holomorphic map of complex variable z=x0+iy and i∈S.Hence,

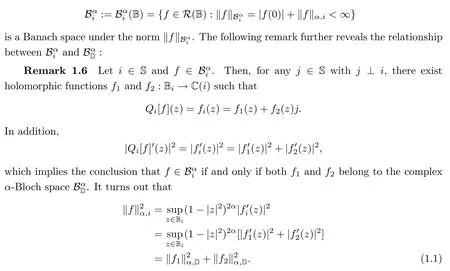
The next proposition shows that the spaces Bαandcontain the same elements.

Proposition 1.7([25,Proposition 2.6]) Let i∈S.Then f∈if and only if f∈Bα.More precisely,one has

In addition,it also holds that

In the sequel,we de fine the composition operator on slice regular α-Bloch spaces.

De finition 1.8Let ?:B→B be a slice regular map such that ?(Bi)?Bifor some i∈S.Then the C(i)-composition operator(C?)i:Bα→Bβof the unit ball B,with the domain consisting of all h∈Bαsuch that C?h belongs to Bβ,is de fined by

Using the Representation Formula,we can obtain all values of C?f on H.

Readers can also refer to[22]for the de finition of the slice regular composition operator C?.It is well-known that the study of composition operators is a fairly active field.For general references on the theory of composition operators on the holomorphic functions of complex variables,see the excellent books[4],by Cowen and MacCluer,and[24],by Shapiro.As regards the slice regular composition operators,Ren and Wang([22])studied their properties acting on the quaternionic Hardy spaces.As a generalization,the basic properties of the slice regular weighted composition operator were systematically characterized in the recent papers[16,18].As far as we are concerned,there has been no investigation on the product operator of differentiation and composition operators acting on slice regular function spaces,so we concentrate on this characterization with regard to Bloch-type spaces.

A natural notion of differentiation can be given for slice regular functions(see[12,13]),and this is called the slice(or Cullen)derivative of f.

De finition 1.9Let ? be a slice domain in H,and let f:?→H be a slice regular function.The slice derivative of f at q=x+yi∈?iis de fined by

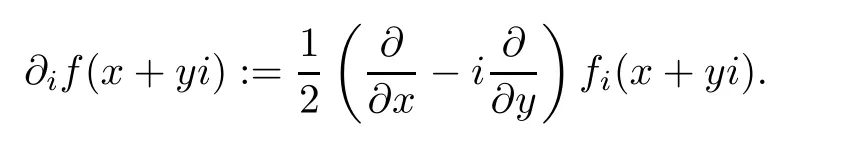
We notice that the operators?iand thatcan commute,and that?if=for regular function f.Therefore,the slice derivative of a regular function is still regular,so we can iterate the differentiation to obtain the m-th slice derivative

In the ensuing sections,we will directly denote the m-th slice derivativef by f(m)for i∈S and m∈N,and denote

Generally,for a nonnegative integer m∈N,we denote

Combining the differentiation operator with a map ? satisfying ?(Bi)?Bifor some i∈S,we de fine the product operator of differentiation and composition operators as

Using the Representation Formula,we can extend all values of the operator C?Dmon R(B).

As is well known,the composition operator is a typical bounded operator on the complex classical Bloch spacewith α=1,while the differentiation operators are typically unbounded on various complex Banach spaces of holomorphic functions.Recently,a lot of work has appeared on new characterizations in terms of ?mfor composition and differentiation operators between complex holomorphic function spaces.For example,Zhao[30]obtained the new characterization for the compactness of composition operator C?fromtoas=0,where ?mmeans the m-th power of ?.For more similar characterizations regarding the boundedness and compactness of some classical linear operators,we refer readers to[3,17,20,27–29]and the references therein.

Regarding the complex-valued product operator C?Dm,we have deduced an equivalent description for its boundedness and estimated its essential norm in terms of monomial znin the complex Bloch-type spaces,which have concise representations,as follows:

Theorem A([19,Theorem 1]) Let 0<α,β<∞,m be a nonnegative integer and let ? be a holomorphic self-map of the unit disk D.Then C?Dm:is bounded if and only if

where z∈D,n∈N.

Theorem B([19,Theorem 2]) Let 0<α,β<∞,m be a nonnegative integer and let ? be a holomorphic self-map of the unit disk D.Suppose thatis bounded,then the estimate for the essential norm of

Building on the above foundations,we continue to provide the corresponding characterizations for the boundedness and essential norm estimation of C?Dm:Bα→Bβof slice regular functions.Throughout the remainder of this paper,N will denote the set of all nonnegative integers and C will denote a positive constant,the exact value of which will vary from one appearance to the next.The notations A?B,AB,AB mean that there may be different positive constants C such that B/C≤A≤CB,A≤CB,CB≤A.

2 The Characterizations for C?Dm:Bα→Bβof Slice Regular Functions

In this section,we first present a characterization for the boundedness of C?Dm:Bα→Bβacting between the slice regular Bloch-type spaces containing Theorem A as a particular case.

Theorem 2.1Let 0<α,β<∞,m be a nonnegative integer and let ?:B→B be a slice regular map such that ?(Bi)?Bifor some i∈S.Then the product operator C?Dm:Bα→Bβis bounded if and only if

where In(p)=pn,p∈H,n∈N.

ProofNecessityAssume that the operator C?Dm:Bα→Bβis bounded.Combining this with Proposition 1.7 ensures that the operator C?Dm:→is bounded.Suppose that p=x0+Iy∈B with some I∈S,and denote z=x0+iy and=x0?iy.It then holds that|z|==|p|.Since

Here we have used(1.1)with In,2(z)=0.Putting the display(2.6)into(2.3)yields that

which,together with the formulas(2.4)and(2.2),implies that

SufficiencySupposing the formula(2.1)holds,we get that

Letting j∈S with j⊥i,it holds that

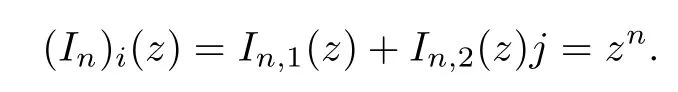
Therefore,by ?(Bi)?Bi,we deduce that

The above arguments,together with(2.7),ensure that

We can verify that H∞(B)is a Banach space under the norm‖f‖∞.Immediately,we go on showing that C?Dm:Bα→Bβis compact if‖?‖∞<1.The following proposition can be deduced by a similar way as[14,Proposition 3.3],which plays a critical role in proving the compactness of operators:

Proposition 2.2Let 0<α,β<∞,m be a nonnegative integer and let ?:B→B be a slice regular map such that ?(Bi)?Bifor some i∈S.Then the product operator C?Dm:Bα→Bβis compact if and only if,for any bounded sequence{fk}k∈Nin Bαwith fk→0 as k→∞on compact sets,‖C?Dmfk‖Bβ→0 as k→∞.

Theorem 2.3Let 0<α,β<∞,m be a nonnegative integer and let ?:B→B be a slice regular map such that ?(Bi)?Bifor some i∈S.If‖?‖∞<1,then the product operator C?Dm:Bα→Bβis compact.

ProofLet{fk}k∈Nbe a bounded sequence in Bαsatisfying fk→0 as k→∞on compact sets of B.Then it also holds that fk→0 as k→∞on compact sets of Bifor i∈S.Let j∈S be such that j⊥i,and let fk,1,fk,2:Bi→C(i)be holomorphic functions satisfying(fk)i(z)=fk,1(z)+fk,2(z)j for some z=x0+iy∈Bi.By Remark 1.6,it follows that the two functions fk,1(z)and fk,2(z)lie in the complex Bloch-type spaceson Bi,where Biis identi fied with D?C(i).In addition,it is obvious that fk,l→0 as k→∞on compact sets of D and l=1,2.Hence we obtain that

where the last line is due to the corresponding result in complex Bloch-type spaces(see,e.g.,[19,page 356])under the case‖?‖∞<1.Based on the fact that

we use(2.8)to deduce that

Employing Proposition 2.2,the compactness of C?Dm:Bα→Bβfollows.

De finition 2.4The essential norm of a bounded linear operator T between two normed linear spaces X and Y is its distance from the compact operator K;that is,

where‖.‖X→Ydenotes the operator norm(see,e.g.,[21]).

It is obvious that T is compact if and only if‖T‖e=0.Thus Theorem 2.3 can yield‖C?Dm‖e=0 for the case‖?‖∞<1.Next,we continue to estimate the essential norm of C?Dm:Bα→Bβunder the case‖?‖∞=1,which contains Theorem B as a special case.

Theorem 2.5Let 0<α,β<∞,m be a nonnegative integer and let ?:B→B be a slice regular map such that ?(Bi)?Bifor some i∈S and‖?‖∞=1.Suppose that C?Dm:Bα→Bβis bounded.Then the estimation for the essential norm of C?Dm:Bα→Bβis

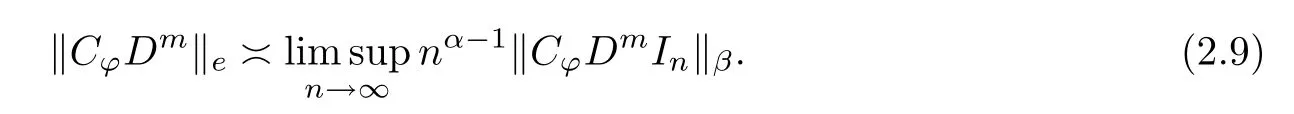
ProofThe lower estimationLet In(p)=pn.Then In(z)=znis a sequence on Bi(identi fied as the unit disk D)associated with n∈N.Since Inconverges to zero uniformly on compact subsets of Bi,Proposition 2.2 ensures that

Here the second and third inequalities are both due to(1.2)in Proposition 1.7.Combining the formula(2.5)with the norm relation in Proposition 1.7,it follows that

The lower estimation follows from the above arguments.

The upper estimationLet Lnbe the sequence of operators given in[19,Lemma 3,4,5];that is,Lnis compact as an operator fromto.Using Remark 1.6,for every f∈,let j∈S be such that j⊥i,and let f1,f2:Bi→C(i)be holomorphic functions satisfying f(z)=f1(z)+f2(z)j for some z=x0+iy∈Bi.It follows that fk∈k=1,2,and so

The formula(1.1)implies that

On the other hand,we turn to estimate the term(2.11).By(1.1),it follows that

which leads to

This further implies that

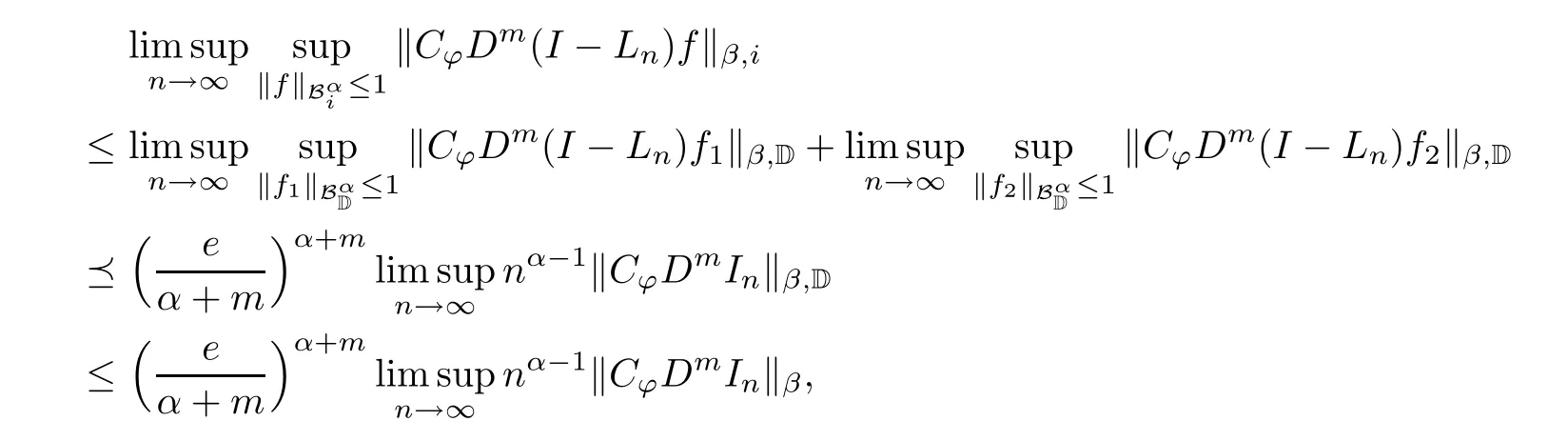
where we use the complex upper estimation(see[19,page 357-359])

completing the proof of the upper estimation.

Remark 2.6Let 0<α,β<∞,m be a nonnegative integer and let ?:B→B be a slice regular map such that ?(Bi)?Bifor some i∈S.Then(2.9)also holds for‖?‖∞<1.

ProofBased on Theorem 2.3,we only need to show that the right part of(2.9)equals 0.Take 0

implying that the formula(2.9)is true.

The last corollary is a consequence of Theorem 2.5 and Remark 2.6.

Corollary 2.7Let 0<α,β<∞,m be a nonnegative integer and let ?:B→B be a slice regular map such that ?(Bi)?Bifor some i∈S.Then the product operator C?Dm:Bα→Bβis compact if and only if

To conclude,we pose a question for exploring in the near future:

QuestionHow does one present the corresponding characterizations for a general slice regular map ?:B→B without the assumption ?(Bi)?Bi?