COARSE ISOMETRIES BETWEEN FINITE DIMENSIONAL BANACH SPACES?
Yuqi SUN(孫玉奇)Wen ZHANG(張文)
School of Mathematical Science,Xiamen University,Xiamen 361005,China
E-mail:sunyuqi00@163.com;wenzhang@xmu.edu.cn
Abstract Assume that X and Y are real Banach spaces with the same finite dimension.In this paper we show that if a standard coarse isometry f:X→Y satis fies an integral convergence condition or weak stability on a basis,then there exists a surjective linear isometry U:X→Y such that‖f(x)?Ux‖=o(‖x‖)as‖x‖→∞.This is a generalization about the result of Lindenstrauss and Szankowski on the same finite dimensional Banach spaces without the assumption of surjectivity.As a consequence,we also obtain a stability result for ε-isometries which was established by Dilworth.
Key words coarse isometry;linear isometry;fi nite dimensional Banach spaces
1 Introduction
Research on the properties of surjective coarse isometries between real Banach spaces started in 1985,when Lindenstrauss and Szankowski[1] first studied a large perturbation function for a surjective standard mapping f between real Banach spaces X and Y which was de fined by

where a mapping f:X→Y is standard if f(0)=0.
They obtained the following result about the asymptotical stability of f:
Theorem 1.1(Lindenstrauss and Szankowski) Let f be a surjective standard map from a Banach space X onto a Banach space Y.If

then there is a linear isometry U from X onto Y such that

At the same time,they showed that condition(1.1)cannot be removed(for details on this one can refer to[2,p.367-370]).
Remark 1.2Dolinar[3]proved that Theorem 1.1 also holds if ?f(t)is substituted by εf(t)in the integral convergence condition(1.1).Here
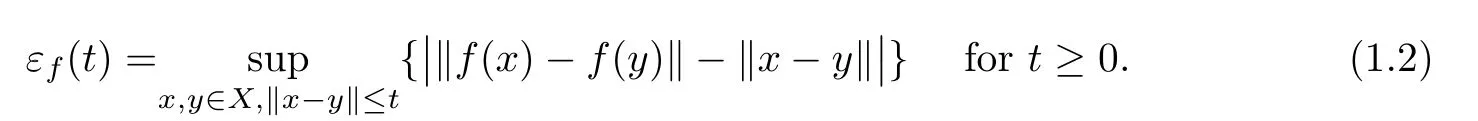
Now let us recall the de finition of coarse isometry.
De finition 1.3Let X,Y be real Banach spaces and let f:X→Y be a mapping,where εf(t)is de fined as in(1.2).f is called a coarse isometry if εf(t)=o(t)as t→∞.In particular,we say that f is an ε-isometry ifεf(t)=ε<∞.
Remark 1.4Note that εf(t)≤?f(t)for each t≥0,so(1.1)implies that ?f(t)=o(t)when t→∞.Then every mapping f:X→Y satisfying(1.1)is a coarse isometry.
As far as we know,when we study a coarse isometry f from a Banach space X to a Banach space Y,it is difficult to find a suitable condition guaranteeing the existencefor each x∈X,even if both X and Y are the real line R.Thus the representation of non-surjective coarse isometries has not been studied until 2019.Cheng et al.[4] first investigated the nonsurjective coarse isometry f:X→Y and obtained the following result,where Y is a uniformly convex Banach space of power type p:
Theorem 1.5(see[4])Suppose that f:X→Y is a standard coarse isometry and that Y is uniformly convex with convexity of type p.If

then there is a linear isometry U:X→Y such that
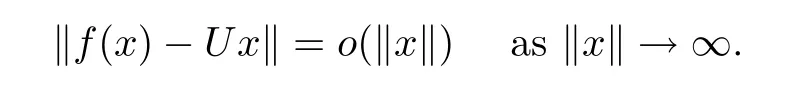
In this paper,we study the properties of non-surjective coarse isometries between the same finite dimensional Banach spaces.In Section 2,inspired by the idea in[5],we prove that if every standard coarse isometry f:X→Y with dimX=dimY<∞satis fies the integral convergence condition

then there exists a surjective linear isometry U:X→Y such that‖f(x)?Ux‖=o(‖x‖)as‖x‖→∞.Here the condition(1.3)is essential,but when the target spaces X,Y are the real line R,the condition(1.3)can be removed.
In Section 3,we prove that if a standard coarse isometry f:X→Y is weakly stable on a basis of X,i.e.,for each x?∈SX?,there exists φ∈SY?such that
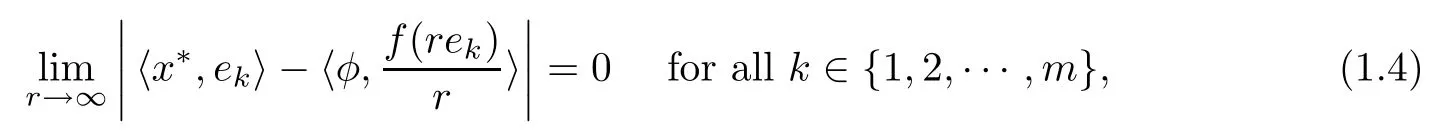
where{ek}?X is a basis.Then there exists a surjective linear isometry U:X→Y such that‖f(x)?Ux‖=o(‖x‖)as‖x‖→∞.Furthermore,we prove that the weakly stable condition is weaker than(1.3)for coarse isometries between the same finite dimensional Banach spaces.As a consequence,we also obtain a stability result for ε-isometry which was established by Dilworth[3,Theorem 2].
Throughout this paper,the letters X and Y are used to denote real Banach spaces,and X?and Y?are their dual spaces.For a real Banach space X,we denote by B(0,1)and°B(0,1)the closed unit ball and the open unit ball of X,respectively.Given a bounded linear operator T:X→Y,T?:Y?→X?is its dual operator.
2 Coarse Isometries Under the Integral Convergence Condition
To begin this section,we recall some related de finitions and results of paracompact spaces,which are taken from[2,p.416–417].
Let Z be a Hausdorffspace.An open cover V is called locally finite if every x∈Z has a neighborhood W that intersects only finitely many sets in V.We say that an open cover V′is a re finement of V if every V′∈V′is contained in some V ∈V.The space is said to be paracompact if every open cover of Z admits a locally finite open re finement.A locally finite partition of unity on Z is a family{Fα:α∈A}of continuous functions from Z to[0,1]such that
(i){{x∈Z:Fα(x)>0}:α∈A}form a locally finite open cover of Z;
We say that the partition of unity{Fα}is subordinated to the cover V if,for each α∈A,{x∈Z:Fα(x)>0}is contained in some V∈V.
Proposition 2.1(see[2]) Metrizable spaces are paracompact.
Proposition 2.2(see[2]) Let Z be a paracompact space.Then for every open cover V of Z,there is a locally finite partition of unity subordinated to V.
The following lemma is essentially inspired by[5,Lemma 2.8]:
Lemma 2.3Let X,Y be Banach spaces and let f:X→Y be a standard coarse isometry.Then there exist a standard continuous coarse isometry g:X→Y and a constant M such that
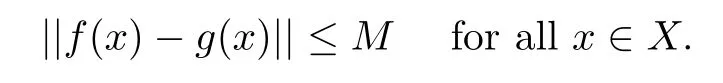
ProofLet{zγ:γ∈Γ}be a maximal set which satis fies the condition that‖zξ?zη‖≥1 if ξη.Let 0∈{zγ:γ∈Γ}.Then,for each x∈X,there is a γ∈Γ such that||x?zγ||<1.Note that{(zγ,1):γ∈Γ}is an open cover of X,hence there exists a locally finite partition of unity{Fα:α∈A}subordinated to{°B(zγ,1):γ∈Γ}.Then for each α∈A,we can choose a γα∈Γ such that{y∈X:Fα(y)>0}?°B(zγα,1).We de fine g:X→Y by
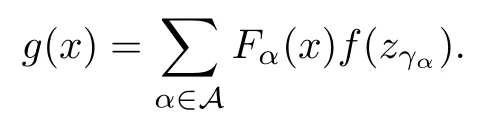
Since,for each γ∈Γ with zγ0,0/∈°B(zγ,1)and for each α∈A with Fα(0)>0,0∈{y∈X:Fα(y)>0}?°B(0,1),g(0)=0.
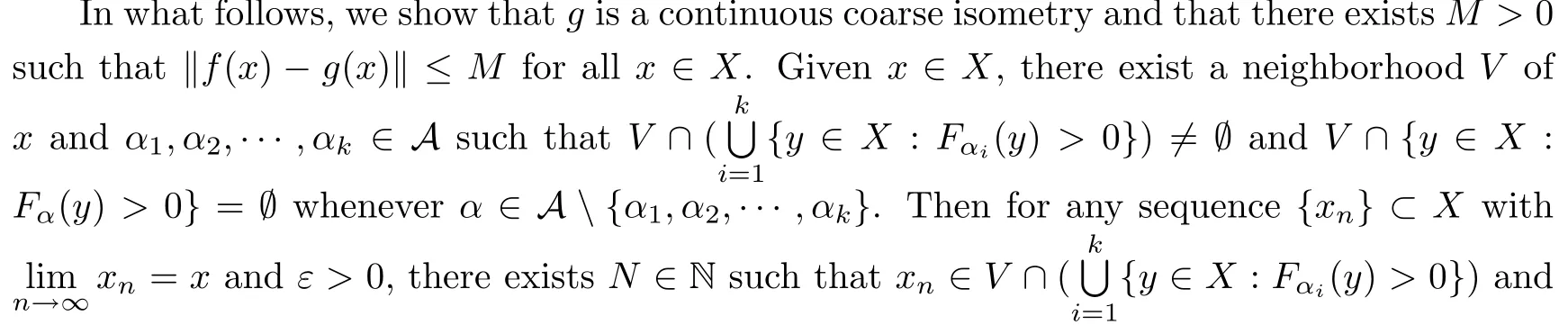

Then g is continuous.Moreover,if Fα(x)>0 for each x∈X,then‖x?‖<1.Consequently,
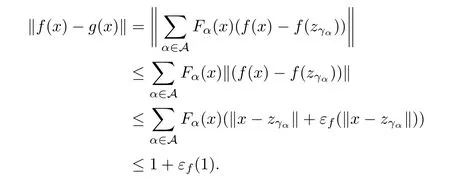
Since f is a coarse isometry,εf(1)<∞.Letting M=1+εf(1),we obtain that‖f(x)?g(x)‖≤M for all x∈X and that εg(t)≤εf(t)+2M,so g is a coarse isometry.
Lemma 2.4([5,Proposition 4.1]) Let X,Y be Banach spaces with dimX=dimY<∞and let f:X→Y be a continuous non-surjective map with‖f(x)‖=∞.Then,given M>0,there are points x,y∈X with‖x?y‖≥M and f(x)=f(y).
Remark 2.5According to Lemma 2.4,we can show that every continuous coarse isometry f:X→Y satisfying the condition dimX=dimY<∞is surjective.Indeed,since f is a coarse isometry,

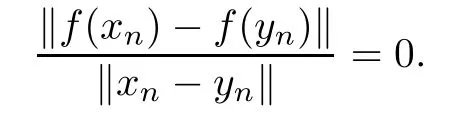
This contradicts(2.1).
The following result is a generalization of Theorem 1.1,where we choose the same finite dimensional Banach spaces(here we don’t need the assumption of surjectivity):
Theorem 2.6Let X,Y be Banach spaces with dimX=dimY<∞and let f:X→Y be a standard coarse isometry.If Z

then there exists a surjective linear isometry U:X→Y such that
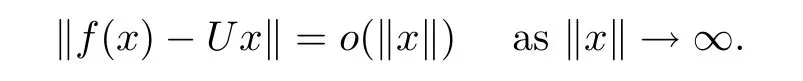
ProofAccording to Lemma 2.3 and Remark 2.5,there exist a constant M and a surjective standard continuous coarse isometry g:X→Y with εg(t)≤εf(t)+2M.Thendt<∞.By Remark 1.2([3,Proposition 1]),there exists a surjective linear isometry U:X→Y such that
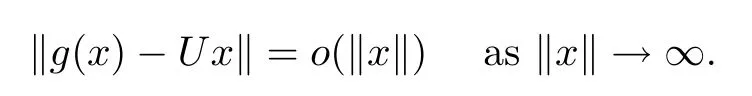
Thus

The following example says that the condition(2.2)in Theorem 2.6 is essential:
Example 2.7Let ?:(0,∞)→(0,∞)be a function de fined by ?(t)=for t>0.Then ? is monotone increasing,and satis fies
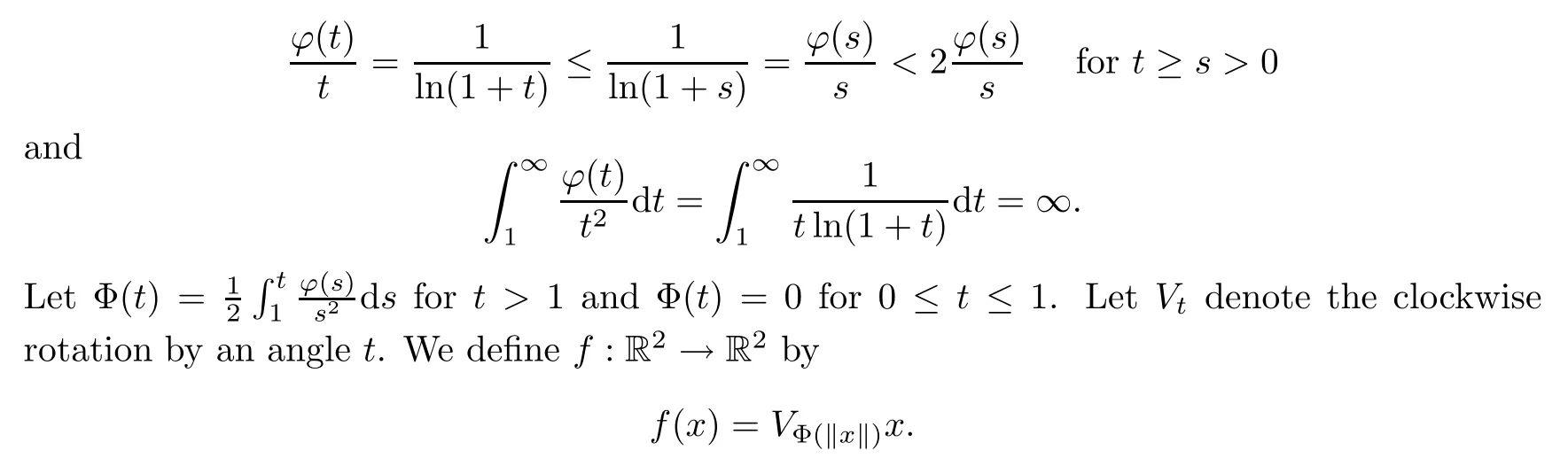
Then by the argument of[2,p.367],there is no isometry U:R2→R2with‖f(x)?Ux‖=o(‖x‖)as‖x‖→∞and εf(t)≤?(t)for all t>0.However f is a coarse isometry.
The next theorem shows that the integral convergence condition(2.2)can be removed when X=Y=R.
Theorem 2.8Let f:R→R be a standard coarse isometry.Then there is a linear isometry U:R→R such that
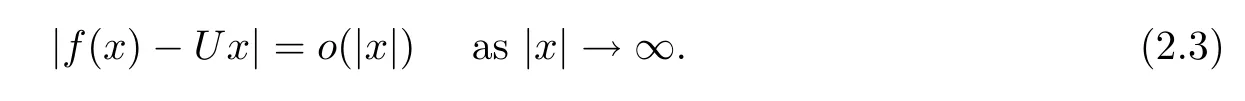
ProofFirst,since f is a coarse isometry,

This is a contradiction.Moreover,we shall prove that
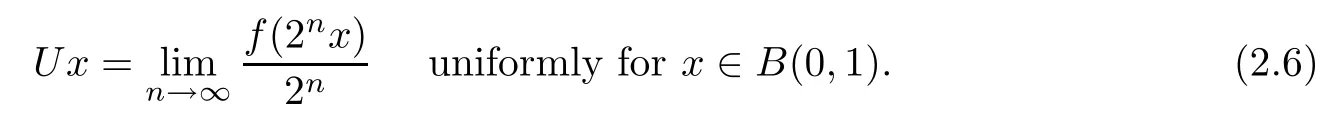
Otherwise,we can find two sequences{xk}?B(0,1),{nk}?N and ε0>0 such that
According to the compactness of B(0,1)in R,without loss of generality,we can assume that xk→x0for some x0∈B(0,1).Then

This contradicts(2.7).
Finally,we show that

This is a contradiction.Thus(2.3)holds.
Corollary 2.9([6,Theorem 2]) Let X,Y be Banach spaces with dimX=dimY<∞and let f:X→Y be a standard ε-isometry.Then there exists a surjective linear isometry U:X→Y such that

ProofAccording to Theorem 2.6,there is a surjective linear isometry U:X→Y such that

Then,by[7,Proposition 2],
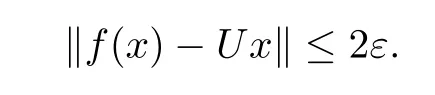
3 Weak Stability of Coarse Isometries
We start this section by recalling the remarkable results for ε-isometries.In 2013,Cheng,Dong and Zhang[8]established the weak stability formula.
Theorem 3.1(see[8])Let X,Y be Banach spaces.Suppose that f:X→Y is a standard ε-isometry.Then,for every x?∈X?,there exists φ∈Y?with‖x?‖=‖φ‖≡r such that

This has played an important role in the study of stability properties of ε-isometries(see[8–13]).Furthermore,the weak stability formula was improved in[14]and[15].
Theorem 3.2(see[14,15])Let X,Y be Banach spaces.Suppose that f:X→Y is a standard ε-isometry.Then,for every x?∈X?,there exists φ∈Y?with‖x?‖=‖φ‖≡r such that
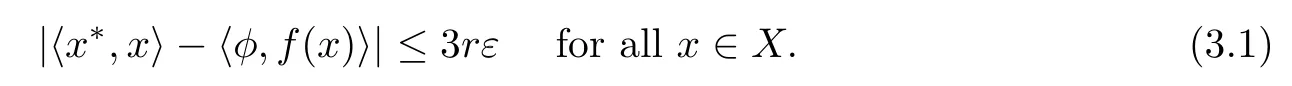
The next result is inspired by the weak stability formula for ε-isometries.
We recall that for a non-empty set ?,a family U of subsets of ? is said to be a free ultra filter provided that
(1)?/∈U,and∩{U∈U}=?;
(2)U,V∈U=?U∩V∈U;
(3)U∈U and U?V??=?V∈U;
(4)A??=?either A∈U,or,?A∈U.
Let U be a free ultra filter,and let K be a Hausdorffspace.A mapping g:?→K is said to be U-convergent to k∈K provided that for any neighborhood V of k,g?1(V)∈U.This means that limUg=k.We should note that every mapping g:?→K is U-convergent when K is compact.
Theorem 3.3Let X,Y be Banach spaces with dimX=dimY=m<∞and let f:X→Y be a standard coarse isometry.If,for each x?∈SX?,there exists φ∈SY?such that

where{ek}?X is a basis,then there exists a surjective linear isometry U:X→Y such that

ProofLet U be a free ultra filter on N and let{rn}n∈N?R with rn→∞as n→∞.Since f is a coarse isometry with f(0)=0,for each x∈X,

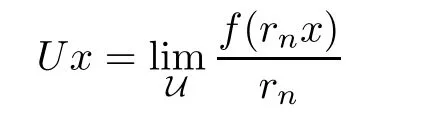
de fines an isometry mapping.According to Remark 2.5 and the Mazur-Ulam theorem[16],we obtain that U:X→Y is a surjective linear isometry,and then U?:Y?→X?is also a surjective linear isometry.
It remains to prove that

Then(3.3)holds,from the proof of(2.6)in Theorem 2.8.
Now we give another proof of[6,Theorem 2]by the weak stability formula for ε-isometries.
Corollary 3.4([6,Theorem 2]) Let X,Y be Banach spaces with dimX=dimY<∞and let f:X→Y be a standard ε-isometry.Then there exists a surjective linear isometry U:X→Y such that

ProofUx=de fines a surjective linear isometry from X onto Y by Theorem 3.2 and Theorem 3.3,so U?:Y?→X?is also a surjective linear isometry.Thus,for each φ∈SY?,

Given δ>0,for each x∈X there exists φ∈SY?such that
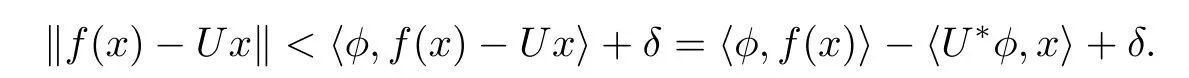
Then‖f(x)?Ux‖<3ε+δ.The arbitrariness of δ entails
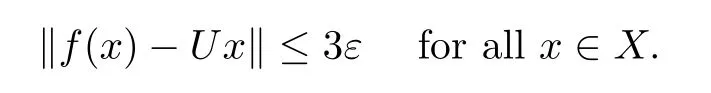
Note that in[7,Proposition 2],it was proved that‖f(x)?Ux‖=o(‖x‖)as‖x‖→∞implies that‖f(x)?Ux‖≤2ε for all x∈X.The proof is completed.
In the proposition and example to follow,we compare the integral convergence condition(2.2)with(3.2)between the same finite dimensional Banach spaces.
Proposition 3.5Let X,Y be Banach spaces with dimX=dimY<∞and let f:X→Y be a standard coarse isometry satisfying
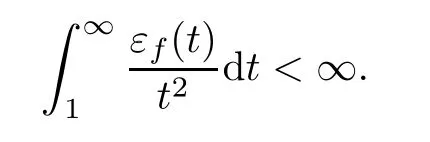
Then(3.2)holds.
ProofAccording to Theorem 2.6,there exists a surjective linear isometry U:X→Y given by

Given x?∈SX?,there exists φ∈SY?such that U?φ=x?,so
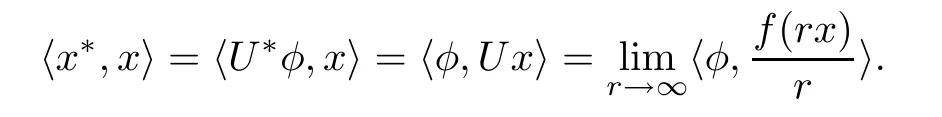
Thus(3.2)holds.
However(3.2)cannot imply the integral convergence condition(2.2).
Example 3.6Suppose that f:R→R is given by
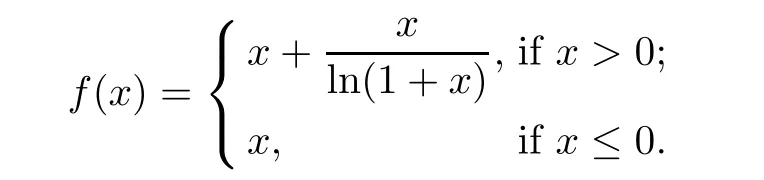
Then f is a standard coarse isometry and(3.2)holds,but

ProofBecause,for t>0
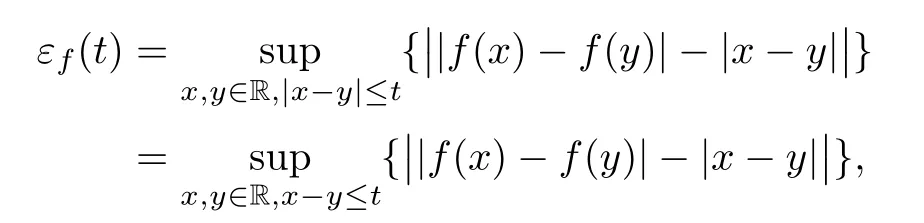
without loss of generality we can assume that y AcknowledgementsThe authors would like to thank the colleagues and graduate students in the Functional Analysis group of Xiamen University for their very helpful conversations and suggestions.
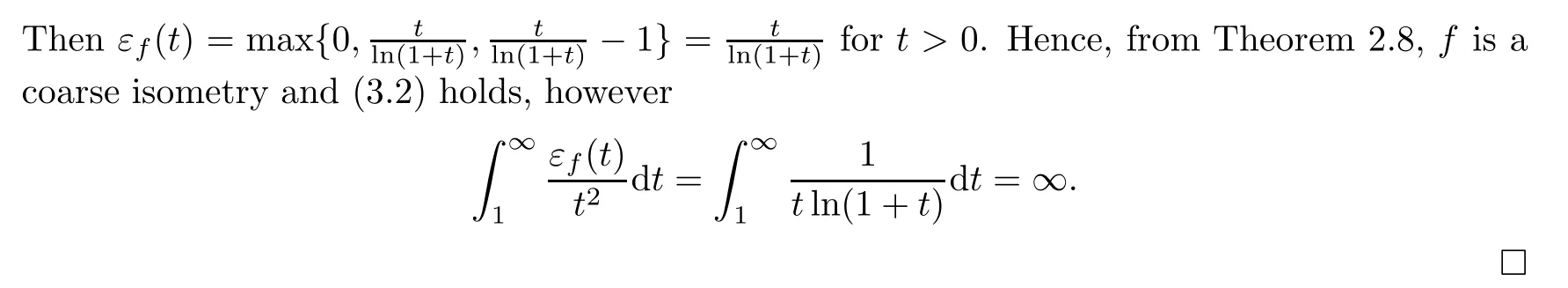
 Acta Mathematica Scientia(English Series)2021年5期
Acta Mathematica Scientia(English Series)2021年5期
- Acta Mathematica Scientia(English Series)的其它文章
- THE UNIQUENESS OF THE LpMINKOWSKI PROBLEM FOR q-TORSIONAL RIGIDITY?
- HYERS–ULAM STABILITY OF SECOND-ORDER LINEAR DYNAMIC EQUATIONS ON TIME SCALES?
- ON NONCOERCIVE(p,q)-EQUATIONS?
- THE CONVERGENCE OF NONHOMOGENEOUS MARKOV CHAINS IN GENERAL STATE SPACES BY THE COUPLING METHOD?
- POSITIVE SOLUTIONS OF A NONLOCAL AND NONVARIATIONAL ELLIPTIC PROBLEM?
- A PENALTY FUNCTION METHOD FOR THE PRINCIPAL-AGENT PROBLEM WITH AN INFINITE NUMBER OF INCENTIVE-COMPATIBILITY CONSTRAINTS UNDER MORAL HAZARD?
