A M Jyothi,R Naveen Kumar,R J Punith Gowdaand B C Prasannakumara

1 Bangalore Institute of Technology,Bangalore,India

2 Department of Studies and Research in Mathematics,Davangere University,Davangere-577002,Karnataka,India

Abstract The current mathematical model explains the influence of non-linear thermal radiation on the Casson liquid flow over a moving thin needle by considering Buongiorno’s nanofluid model.The influences of Stefan blowing,Dufour and Soret effects are also considered in the model.The equations which represent the described flow pattern are reduced to ordinary differential equations (ODEs) by using apt similarity transformations and then they are numerically solved with Runge–Kutta-Fehlberg’s fourth fifth-order method (RKF-45) with shooting process.The impacts of pertinent parameters on thermal,mass and velocity curves are deliberated graphically.Skin friction,rate of heat and mass transfer are also discussed graphically.Results reveal that,the increase in values of Brownian motion,thermophoresis,Dufour number,heating and radiative parameters improves the heat transfer.The increasing values of the Schmidt number deteriorates the mass transfer but a converse trend is seen for increasing values of the Soret number.Finally,the escalating values of the radiative parameter decays the rate of heat transfer.

Keywords: moving thin needle,Brownian motion and thermophoretic diffusion,non-linear thermal radiation,Stefan blowing condition

Nomenclature

1.Introduction

The boundary layer stream with thin needles has extensive applications in biomedical and engineering fields.For example,it is generally used in a protected thermocouple to calculate wind velocity,hot wire anemometer,wire coating and circulatory problems.Recently,Mabood et al [1] examined the consequences of chemically reacting cross stream of non-Newtonian fluid through a thin moving needle.Souayeh et al[2]deliberated the non-linear thermal radiation impact on the Casson liquid flow through a needle with thermophoresis and Brownian motion.Ramesh et al[3]examined the hybrid nanoliquid flow through a needle.Xiong et al [4] illustrated the dissipative flow of cross nanofluid past an upright thin needle.Kumar et al [5] deliberated the particle deposition on the Casson liquid flow past a thin moving needle.

Due to an increase in industrial and technological uses in recent years,the non-Newtonian liquid flow is attracting the attention of more researchers.For example,if a person uses non-Newtonian liquids as coolers or heat exchangers,the required suction capacity can be greatly reduced.The characteristics of non-Newtonian liquids are different from those of the viscous liquid.Non-Newtonian liquid levels are relatively uneven and more complex compared to Newtonian liquids.In the literature,it is sometimes said that in many aspects,the Casson model is better than that of the standard visco-plastic model for rheological data entry.Therefore,it becomes the preferred rheological model of blood and chocolate.Recently,Ramesh et al[6]analysed the steam of Casson liquid past an extending sheet with Catteneo-Christove heat diffusion.Ibrar et al[7]explicated the influence of thermal radiation on Casson fluid stream with suspension of nanoparticles through a thin needle.Hamid [8] deliberated the viscous-ohmic dissipative stream of Casson fluid past a thin needle with nanoparticles suspension.Kumar et al[9]explicated the Casson and Carreau nanofluid streams with porous medium.Khan et al [10] pondered the Casson liquid flow through a stretchy surface with radiation effect.

Brownian movement and thermophoresis are the methods of mass and heat transfer of small particle movements in the form of thermal decay and concentration gradients which affect the small particles associated with bulk surfaces.The thermophoresis and Brownian movements are important factors in heat and mass transfer problems.It is widely used in various fields such as nuclear safety systems,aerospace,hydrodynamics,aerosol technology,and air pollution.In recent days,several researchers deliberated the thermophoresis effect and Brownian movement on the liquid flow through diverse surfaces.Hussain and Ahmed[11] studied the flow of liquid through a porous enclosure by using Buongiorno’s nanofluid model.Khan et al[12]scrutinized the Brownian motion and thermophoresis effects on nanoliquid stream through a microchannel with a radiation effect.Jayadevamurthy et al[13]explicated the bioconvective stream of hybrid nanofluid through a moving rotating disk by considering thermophoresis and Brownian motion effects.Khan et al[14]utilized Buongiorno’s nanofluid model to deliberate the non-Newtonian liquid stream through stretchy surface.Hayat et al[15]explored the non-Newtonian liquid flow by using thermophoresis and Brownian motion effects.

The importance of radiation plays a vital role in many physical problems.Radiation is a heat transference process that distributes heat energy through fluid particles.The impact of radiation on the stream of liquids reflects a major characteristic of engineering and many industrial developments including high temperatures,such as the production of paper plates,freezing of metal fragments,the manufacture of electrical chips,and fuel pumps.Recently,Hussain[16]discussed the dissipative flow of fluid with radiation effect.Sheikholeslami et al [17] scrutinized the impact of thermal radiation on nanoliquid stream.Mehmood et al [18] expounded the radiative flow of nanoliquid by means of KKL-model.Khan et al [19] inspected the radiative stream of non-Newtonian liquid with nanoparticles suspension.Gowda et al [20]explicated the radiative stream of second grade nanofluid.

In many cases,it has been observed that there is a high concentration of extracellular species that can cause the impact of a blow.The idea of the impact of blowing comes from Stefan’s problem.Stefan flow refers to the movement of the effects of chemical reactions from the scattering of species on the visual connector which can create a blowing effect.This explosion effect can occur in an inert position and is therefore completely different from the suction effect on the wall associated with the injection in open areas.The concept of wall injection is presented in the Stefan problem and was first investigated by Spalding [21].Encouragement of the Stefan blowing constraint on a stream of nanofluid past a solid rotating stretchy disk was scrutinised by Latiff et al[22].Amirsom et al [23] numerically explained the stimulation of Stefan blowing on the convective stream of nanoliquid past a thin needle with microorganisms.Alamri et al [24] schematically depicted the significance of Stefan blowing on the Poiseuille nanofluid flow over the parallel plates.Lund et al[25] reported a model for studying the impact of Stefan blowing on the Casson nanofluid stream in the occurrence of radiation effect.

The thermal-diffusion (Soret) effect is the mass transfer caused by a thermal gradient.The Diffusion thermo effect,also known as the Dufour effect,is the energy flux produced by a composition gradient.The Soret-Dufour effects are generally smaller in magnitude than the effects defined by Fourier’s and Fick’s rules,and they are often ignored in mass and heat transport phenomena.In addition,the Dufour and Soret effects in the presence of thermal radiation have practical uses in solar power technology,electrical power generation,high temperature systems,nuclear reactors,and many other fields.Recently,Hayat et al[26]deliberated the Dufour-Soret effects on radiative flow of second grade liquid above an elastic sheet.Khan et al [27] explicated the Dufour-Soret effects on convective flow of Carreau–Yasuda fluid.Imtiaz et al [28] expounded the Dufour-Soret effects on flow of viscous liquid past a curved elastic surface.Jawad et al [29]elucidated the radiative flow of liquid with Marangoni convection and Dufour-Soret effects.

Inspired by literature mentioned above,this study investigates the impact of non-linear thermal radiation on Casson liquid flow past a moving thin needle with Stefan blowing,Dufour,Soret,thermophoresis and Brownian motion effects.This model as practical applications in the development of novel surgical devices for cell conveyance to the central nervous system.Blood flow in the blood vessels is a communal example of Casson liquid stream among other innovative applications of this liquid model.Graphs are drawn for various parameters against velocity,temperature and concentrations gradients.Results are modified to limited cases to make reasonable study.

2.Governing equations and physical description

In this problem,we consider the model of steady flow and heat transfer analysis of Casson nanofluid over a moving thin needle with a constant velocityUwin a parallel free stream as shown in figure 1.The influences of non-linear radiation along with Stefan blowing,Soret and Dufour effects are also invoked.Furthermore,the room temperature and the concentration of the needle are supposed to be fixed,such thatTw>T∞andCw>C∞.Further,the shape of the thin needle is specified byin which composite velocityU=Uw+U∞≠0.Flow is laminar and the slippage is ignored.The needle is considered thin when its thickness does not exceed that of the boundary layer over it.Since,the needle is assumed to be thin,it is also assumed that the effect of its transverse curvature is of importance but the pressure gradient along the body may be neglected.

The governing equations of the above assumed flow are given by ([30–32]):

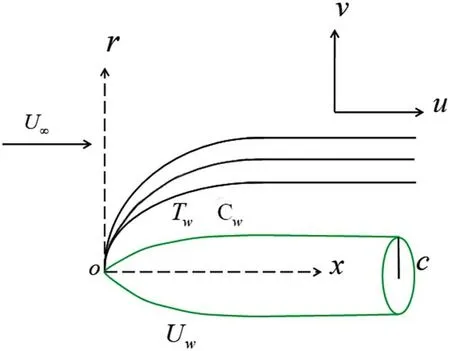
Figure 1.Flow geometry of the considered physical model.

The boundary constraints for the current study are as follow:

Stream function and similarity variables for the developed governing equations are as follow:

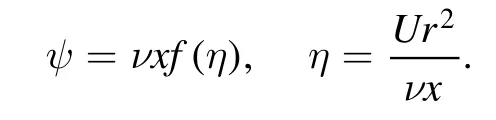
After implementation of the similarity variables,equation (1) is automatically satisfied and the remaining expressions are converted as:

Corresponding reduced boundary conditions are given by:

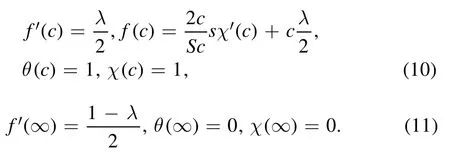
Where,s< 0 signifies mass suction ands> 0 signifies mass blowing as defined in [33].

Where,dimensionless parameters are defined as follows:

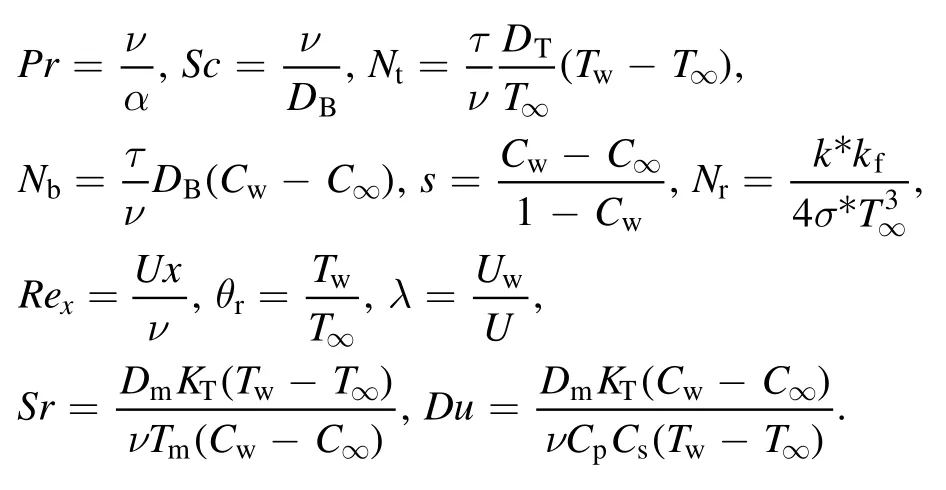
Mathematically,the surface drag force,rate of heat and mass transfer are given by:

3.Numerical method

For various values of pertinent governing parameters,an efficient RKF-45 technique is employed to integrate the equations (7)–(9) along with the corresponding boundary constraints (10),(11).Initially,a two-point boundary value problem is reduced into first order differential equations.Also,to guess the missing initial conditions a shooting scheme is employed.Later,by using the RKF-45 method the resultant one is integrated.Here,the process uses a fourth- and a fifthorder Runge–Kutta scheme.The error of this algorithm can be found by subtracting these two values,and utilized for adaptive step sizing.The algorithm of the RKF-45 process is as follows:

The value ofη∞is chosen in such a way that the boundary conditions are asymptotically satisfied.The step size is selected asΔη= 0.001 with error tolerance to 10-6is well-thoughtout for convergence.Table 1 represents the comparative studyof existing works with present results and found a good agreement with each other.

Table 1.The comparison of f ′′( c) values for some reduced cases whenλ = 0.

4.Results and discussions

In this present examination,the non-linear thermal radiation impact on the stream of Casson fluid over a thin needle by means of Buongiorno’s nanofluid model is discussed.At the boundary of the needle Stefan blowing effect is considered.The equations which govern the flow are converted to ODEs by choosing apt similarity variables.The impact of several dimensionless parameters like Casson parameter,heating parameter,radiative parameter,Schmidt number,Stefan blowing parameter,thermophoresis and Brownian motion parameters on concentration,thermal and velocity profiles are explicated graphically.Also,skin friction,rate of mass and heat transfer are deliberated graphically.Prandtl number has been specified to be adjusted for all of this while other parameters are set to be varied to assess their effects in terms of flow,heat and mass transfer.

Figure 2 portrays the domination ofβ* onf′(η)for the casesλ= 1 andλ= -1.Here,λ= 1 specifies the case of the moving needle in a sedentary ambient liquid andλ= -1 represents the free-streams wings in the negative x-direction.The escalating values ofβ* declines thef′(η)for the caseλ=1 while contrary movement is depicted inf′(η)for the caseλ= -1.Physically,a rise in values ofβ* advances the liquid viscosity which results in declination off′(η).Figure 3 demonstrates the sway ofsonf′(η).An increase insimproves thef′(η).We have detected that as the Stefan blowing parameter values upsurges,friction factor at the surface increases that is,week lateral mass flux into the boundary layer upsurges.The domination ofNbonθ(η) is revealed in figure 4.The growing values ofNbimproves theθ(η).From a physical point of view,the growing value ofNbincreases the thermal conductivity which automatically improves the thermal gradient.Figure 5 portrays the domination ofNtonθ(η) .Here,inclination inNtinclines theθ(η) .Physically,for a warm surface(Nt>0) ,thermophoresis impact improves the concentration of nanoparticles.Meanwhile,a hot needle fends off submicron particles which results in forming a particle-free layer near the surface.The encouragement ofNronθ(η) is portrayed in figure 6.It is clear that,escalating values ofNrimproves the thermal gradient.This is due to the physical fact that the inclination inNrimproves the thermal diffusivity which results in augmentation ofθ(η) .Figure 7 portrays the impact ofθronθ(η) .The upsurge inθrimproves theθ(η) .Physically,the inclination inθrimproves the inner temperature of liquid particles which results in augmentation ofθ(η) .Figure 8 illustrates the effect ofDuover temperature profile.As the values ofDuincreases slightly,the thermal distribution increases.The thermal diffusion increases asDuincreases which augments the temperature.Figure 9 explains the aspect ofSconχ(η) .The enhancing values ofScweakens theχ(η) .Physically,the upsurge in Schmidt number lessens the molecular diffusivity which results in decay of mass transfer.Figure 10 depicts the impact ofSronχ(η) .The upsurge inSrimproves the concentration gradient.Higher values ofSrreasons for low friction which in turn augments theχ(η) .Figure 11 displays the impact ofλon skin friction versus Casson parameter.Here,the skin friction improves for the caseλ= 1 but converse trend is depicted for the caseλ= -1.The impact of radiative parameter on the heat transfer rate is showed in figure 12.The increase inNrvalues decay the rate of heat transfer.The sway of Stefan blowing parameter on mass transfer rate is portrayed in figure 13.The gain insdeteriorates the rate of mass transfer

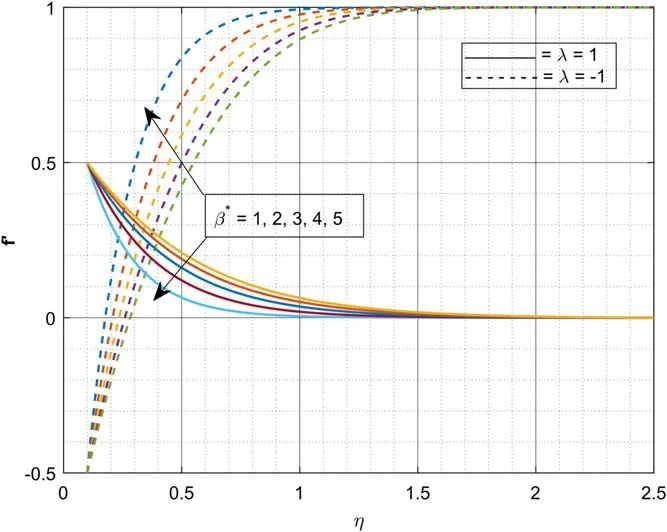
Figure 2.Domination of β* on f′ .

Figure 3.Domination of s on f′ .

Figure 4.Domination of Nb onθ.

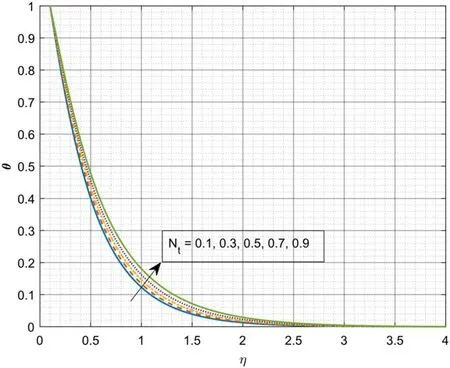
Figure 5.Domination of Nt onθ.

Figure 6.Domination of Nr onθ.

Figure 7.Domination ofθr onθ.

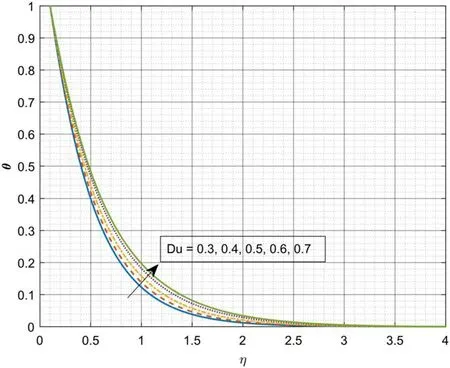
Figure 8.Domination of Du onθ.

Figure 9.Domination ofSc onχ.

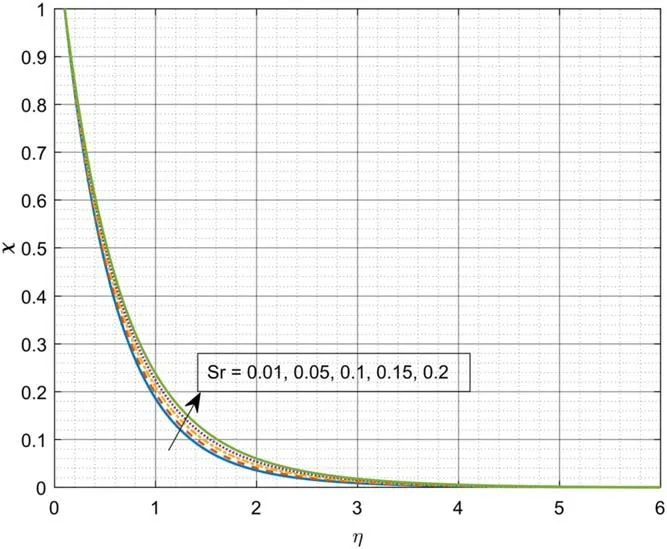
Figure 10.Domination ofSr onχ.

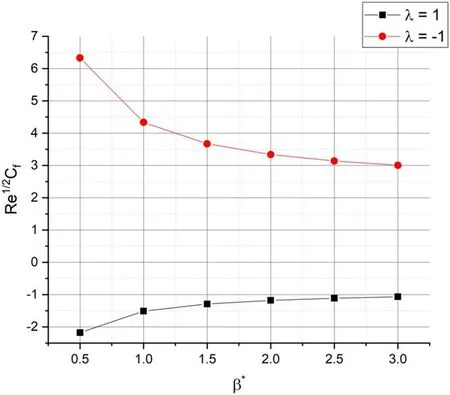
Figure 11.Domination ofλ on Rex 1 /2C f.

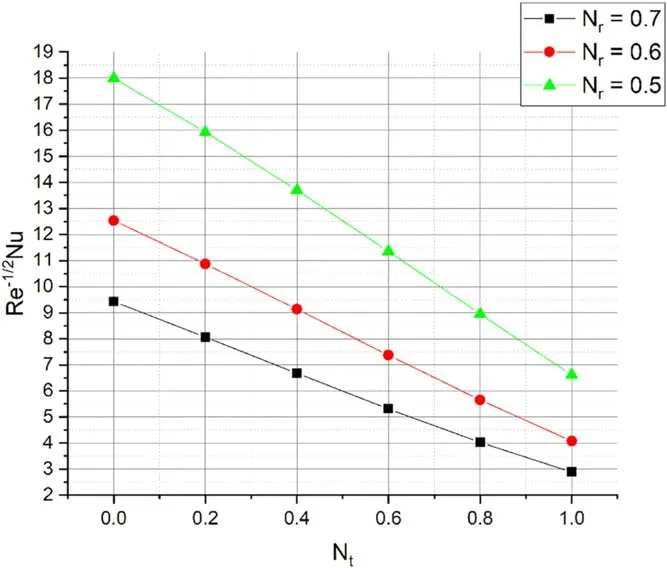
Figure 12.Domination of Nr on Rex 1 /2Nu.

Figure 13.Domination of s on Rex 1 /2S h x.

5.Conclusions

The present investigation explains the salient aspects of the incitement of non-linear thermal radiation on the Casson liquid stream over a moving thin needle with Stefan blowing,thermophoresis and Brownian motion effects.The influences of Dufour and Soret are also considered in the model.The impact of pertinent parameters on thermal,mass and velocity curves are deliberated graphically.The following conclusions are obtained from the present study:

? The growing values ofNbprogresses the thermal gradient due to an increase in the thermal conductivity.

? The escalating values ofNrandθrimproves the inner temperature of liquid particles resulting in an improvement in heat transfer.

? An upsurge in theSclessens the molecular diffusivity and it results in declination of mass transfer.

? The enhancing values ofNtimprove the heat transfer.

? The thermal diffusion increases asDuincreases which augments the temperature.

? Higher values ofSrreasons for low friction which in turn augments the mass transfer.

ORCID iDs