Hui-Ling Wu (吳慧伶), Sheng-Wan Fan (樊盛婉), Jin-Xi Fei (費金喜) and Zheng-Yi Ma (馬正義),3

1 Institute of Nonlinear Analysis and Department of Mathematics,Lishui University,Lishui 323000,China

2 Institute of Optoelectronic Technology and Department of Photoelectric Engineering, Lishui University,Lishui 323000, China

3 Department of Mathematics, Zhejiang Sci-Tech University, Hangzhou 310018, China

Abstract For a one(2+1)-dimensional combined Kadomtsev-Petviashvili with its hierarchy equation,the missing D’Alembert type solution is derived first through the traveling wave transformation which contains several special kink molecule structures.Further,after introducing the B?cklund transformation and an auxiliary variable, the N-soliton solution which contains some soliton molecules for this equation,is presented through its Hirota bilinear form.The concrete molecules including line solitons, breathers and a lump as well as several interactions of their hybrid are shown with the aid of special conditions and parameters.All these dynamical features are demonstrated through the different figures.

Keywords: Kadomtsev-Petviashvili equation, soliton molecule, breather/lump soliton, elastic interaction

1.Introduction

It is well known that the standard Kadomtsev-Petviashvili(KP) equation can be written as (v ≡v(x, y, t))

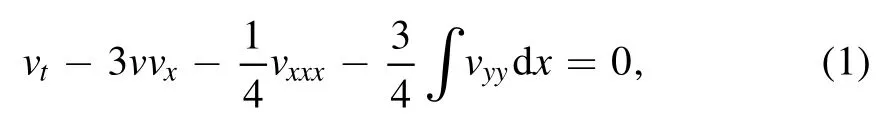
which possesses the quadratic nonlinearity vvxand a weak dispersion vxxx[1].Equation(1)admits the weakly dispersive waves in a paraxial wave approximation and can also be described as the evolution of long ion-acoustic waves of small amplitude propagating in plasma physics under the effect of long transverse perturbations [2, 3].

The KP hierarchy is a paradigm of the hierarchies of one integrable system and includes an infinite number of integrable nonlinear differential equations [4–6].Generally speaking, integrable equations possess properties such as Lax pair, an infinite number of conservation laws and multiple soliton solutions.These nonlinear wave equations that model complex physical phenomena have attracted more and more attention from different fields [7–13].The following member of the KP hierarchy[14]is derived through the pseudo-differential formalism [15].Its multiple soliton solutions are obtained mainly using a simplified version of Hirota’s method [16].

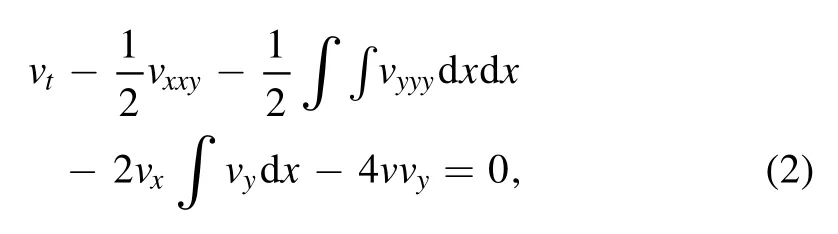
In fact, an integrable nonlinear equation combined with another will often produce unexpected results [17–20].Inspired by this idea, we employ the following integrable system which is extended and combines the (2+1)-dimensional KP equation (1) with the KP hierarchy (2) (KP-h)

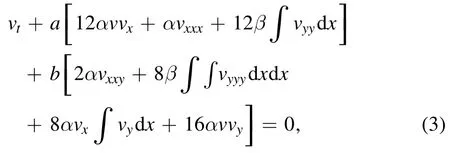
to illustrate the related soliton structures and some nonlinear phenomena.Here, the parameters a, b, α and β are four real constants.Whenand a=1, b=0,equation (3) is just the KP equation (1), but a=0, b=1,equation (3) is the KP hierarchy (2).

This system (3) is integrable and its Lax pair can be derived as (ψ ≡ψ(x, y, t), Ψ ≡Ψ(x, y, t))

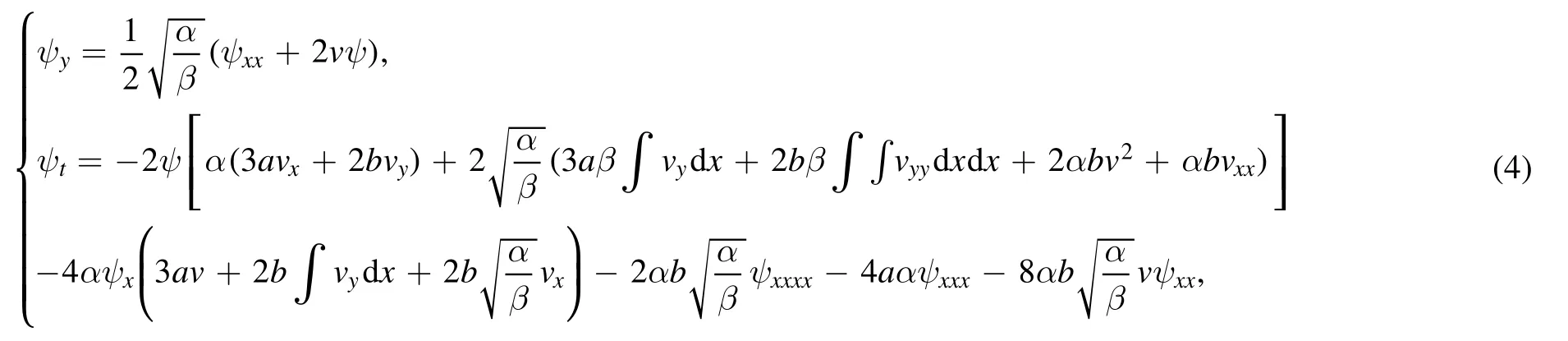
and its dual

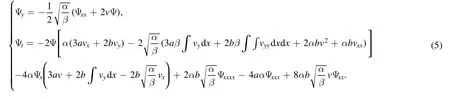
The outline of this paper is as follows:In section 2,after taking the traveling wave transformation, the missing D’Alembert type solution is derived which contains several special kink molecule structures for the (2+1)-dimensional Kadomtsev-Petviashvili with its hierarchy equation (3).In section 3, after introducing the B?cklund transformation and an auxiliary variable τ, the Hirota bilinear form of this equation is conducted, the N-soliton solution which contains some soliton molecules is presented.These concrete molecules include the line solitons, the breathers and a lump as well as several interactions of their hybrid after studying some special conditions and parameters.These dynamic features are demonstrated using the different figures.In the last section, a brief summary is given for this paper.

2.The D’Alembert type solutions of the (2+1)-dimensional KP-h system

Recently, Lou studied the cKP3-4 equation and the Nizhnik-Novikov-Veselov (NNV) equation to investigate various types of solitons including the missing D’Alembert type solutions, the arbitrary traveling waves moving in one direction with a fixed model dependent velocity and soliton molecules [21, 22].In fact, this (2+1)-dimensional KP-h system (3) may have the same properties.For this purpose,we rewrite equation (3) as (u ≡u(x, y, t), w ≡w(x, y, t))

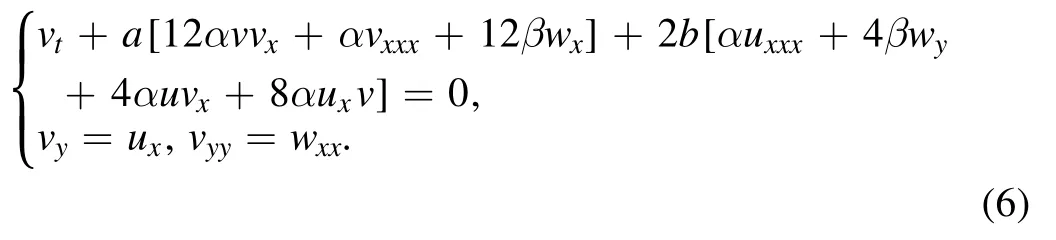
After taking the traveling wave transformation

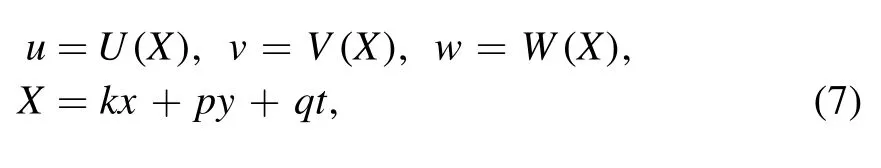
Equation (6) becomes

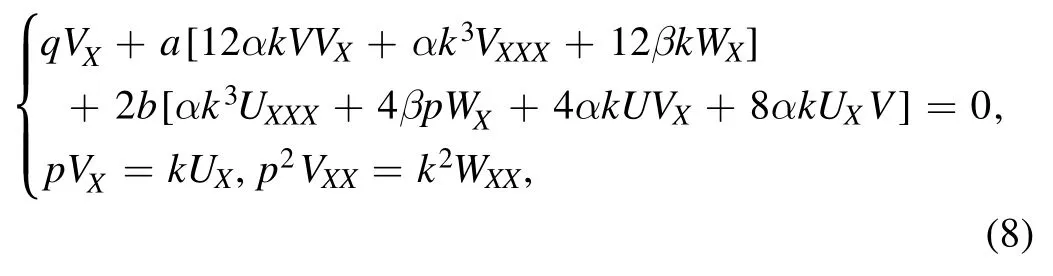
which can be derived as

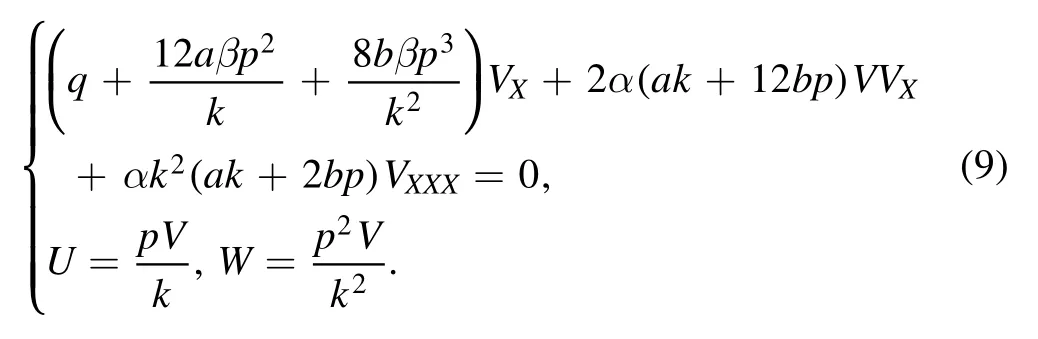
This equation induces

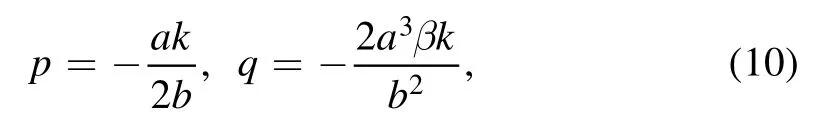
and

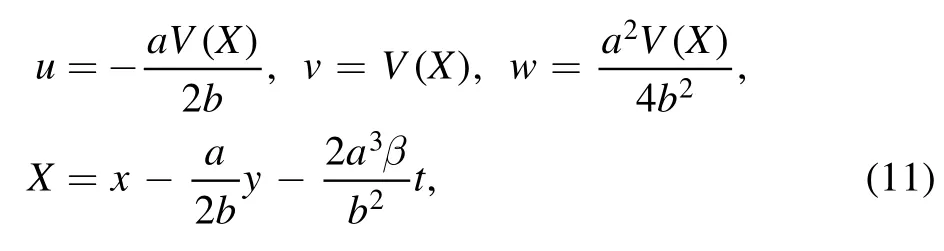
where the traveling wave V becomes an arbitrary D’Alembert type wave.This solution contains several special Kink molecule structures through equations(9)–(11).For example,when the related parameters are

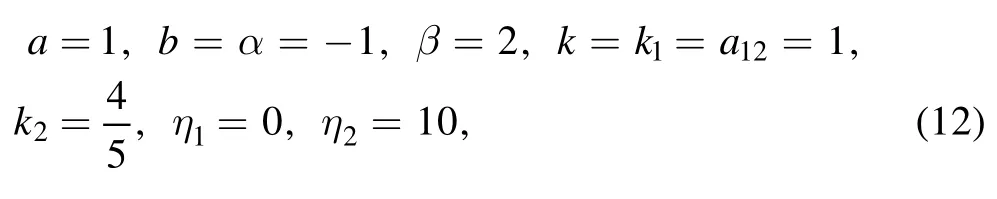
while the solution v=V(X) of equation (3) is

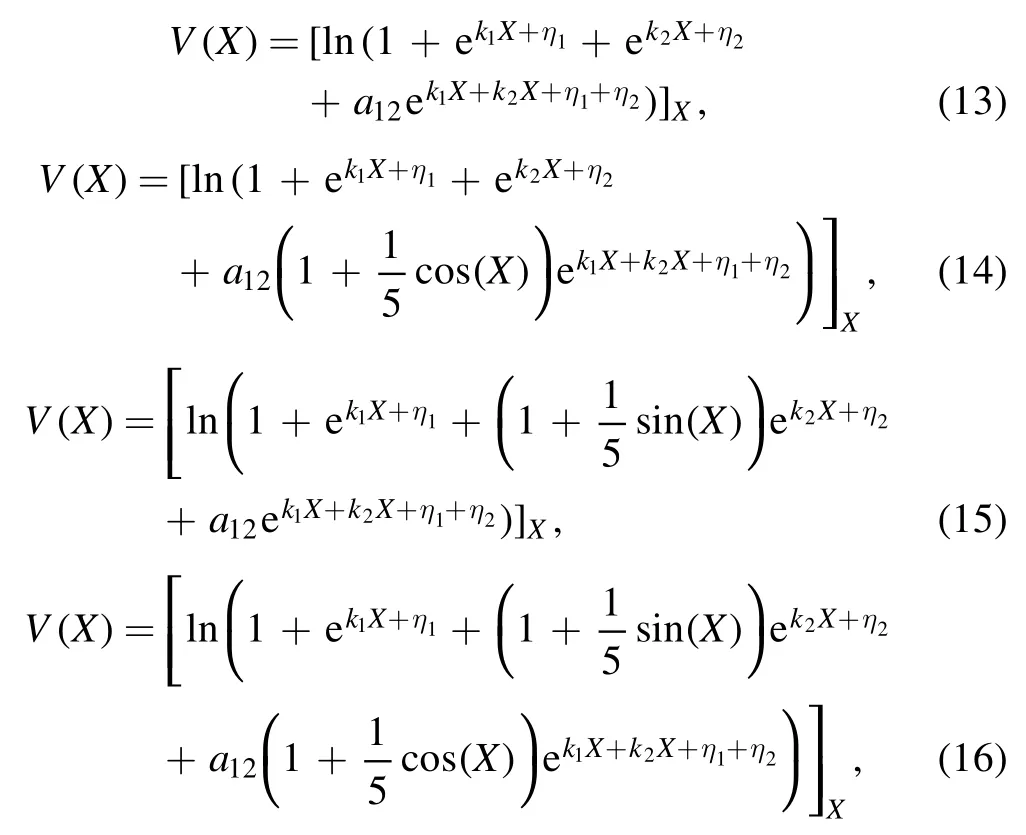
we can present a kink molecule(figure 1(a)),a kink and a half periodic kink (HPK) molecule (figure 1(b)), a HPK-HPK molecule (figure 1(c)) and a HPK-PK molecule (figure 1(d)),respectively at time t=0 [20–22].

Figure 1.(a)Kink molecule expressed by equations(12)and(13);(b)Kink-HPK molecule given by equations(12)and(14);(c)HPK-HPK molecule described by equations (12) and (15); (d) HPK-PK molecule defined by equations (12) and (16) at time t=0.

3.The soliton molecule solutions of the (2+1)-dimensional KP-h system

To derive the soliton molecule solutions of the (2+1)-dimensional KP-h system(3),we first introduce the following B?cklund transformation (f ≡f(x, y, t))

Then,the trilinear form in terms of the auxiliary function f can be written out through equation (3)

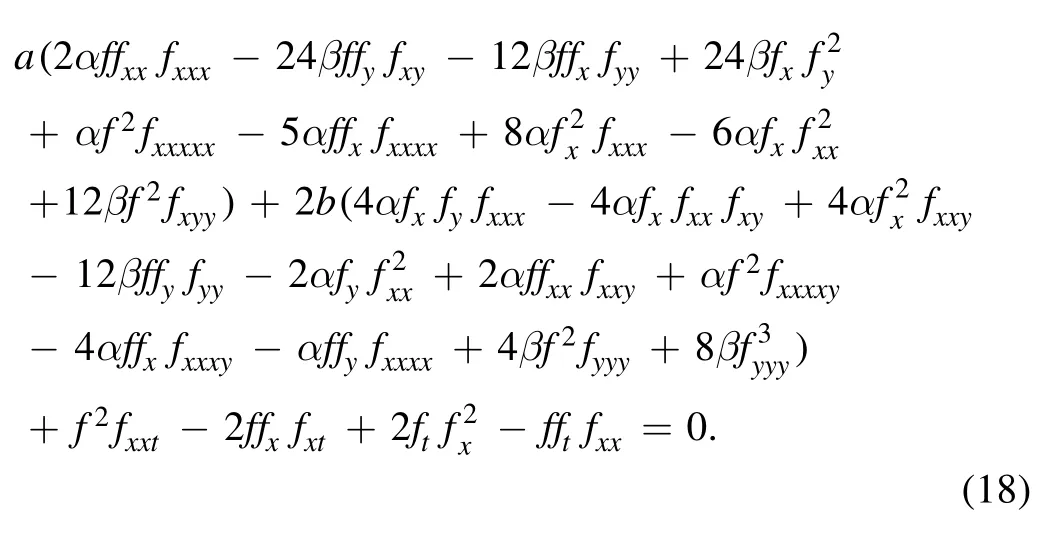
Further, we introduce an auxiliary variable τ, such that this trilinear equation (18) can be bilinearized directly

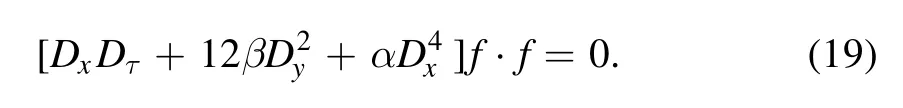
After that, equation (18) becomes

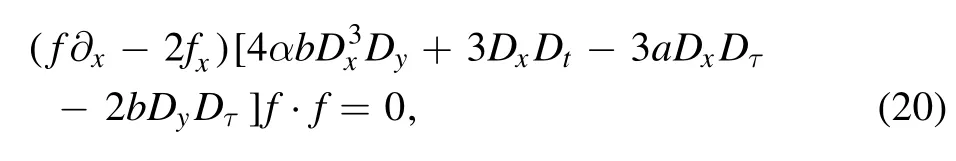
which can be solved through the bilinear equation

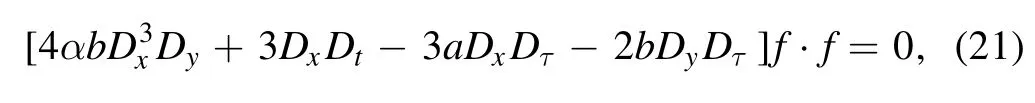
with the D-operator defined by [23]

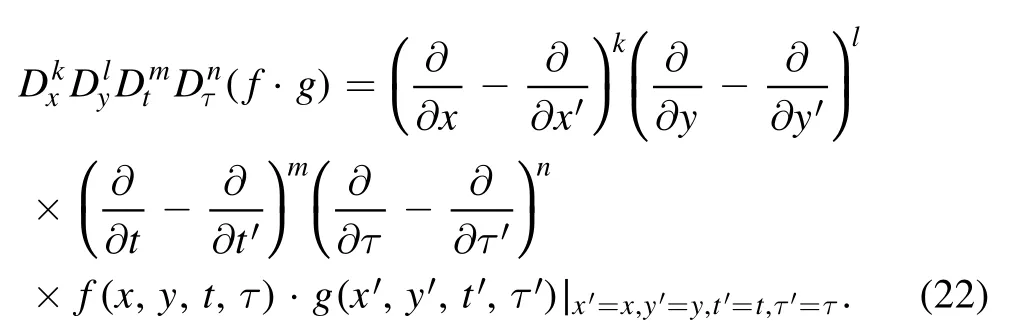
Therefore, the N-soliton solutions described through equation(17)of the(2+1)-dimensional KP-h system(3)also have the following standard expression for the auxiliary function f

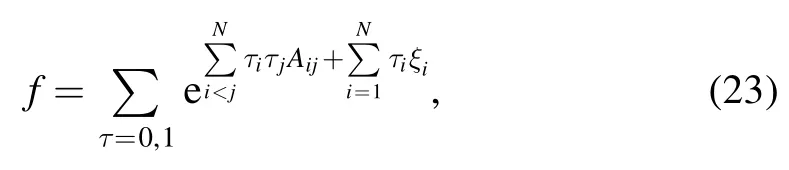
from equation (21) [24–28], while the relations of the parameters are

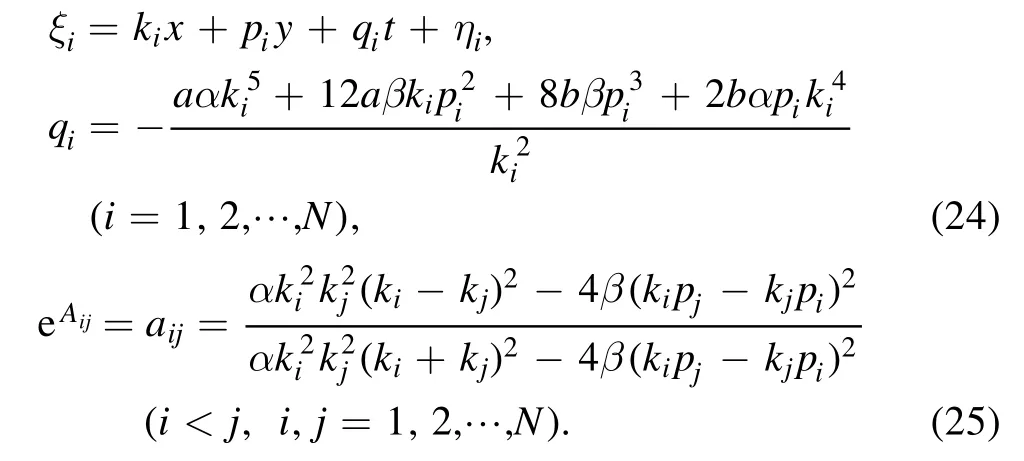
These multiple soliton solutions of equations (17) with(23) may contain many kinds of resonant excitations [29, 30].In the following, we try our best to derive the soliton molecules,the breathers through the resonant condition,the rational lumps by further limit condition and their hybrid structures for the above conclusion.The concrete formula of the auxiliary function f of equation (23) for N=4 can be rewritten as

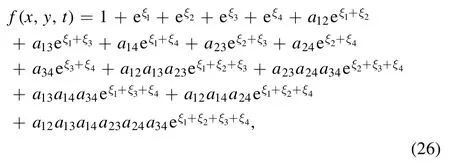
where the phase shifts aij(i ＜j, i, j=1, 2, 3, 4) and the parameters qi(i=1, 2, 3, 4) satisfy equations (24) and (25).

In order to construct soliton molecules, we use the following velocity resonant conditions:

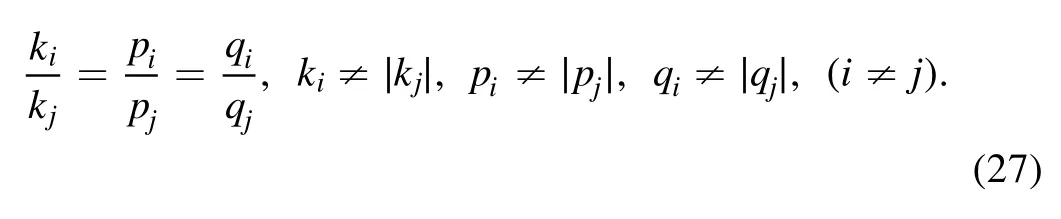
(1) The molecules produced by the solitons

· One two-soliton molecule

We first take the above phase shifts aij=0(j=3, 4) and ξi=0(i=3, 4) in equation (26), and require the velocity resonant condition (27) for i=1, j=2.The soliton molecule structure is satisfied with the condition

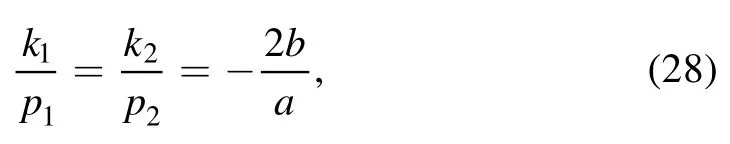
from equations (24) and (25) for a12, q1and q2.

Figure 2(a)exhibits the two-soliton molecule after taking the determining parameters

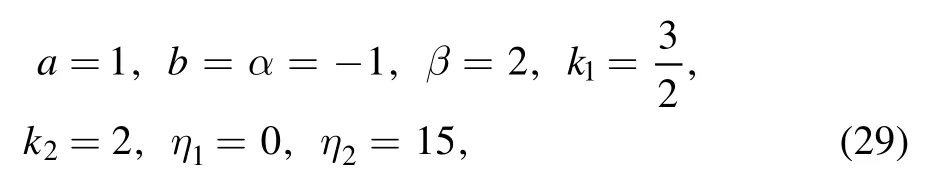
which lead to the other parameters’ values

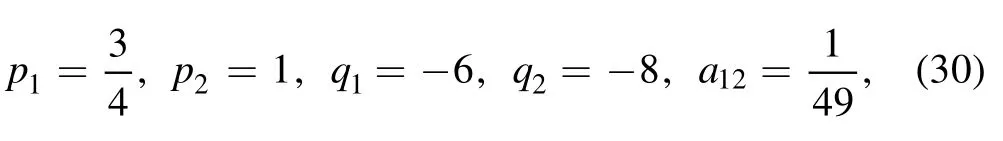
In this case, the the auxiliary function f is given by

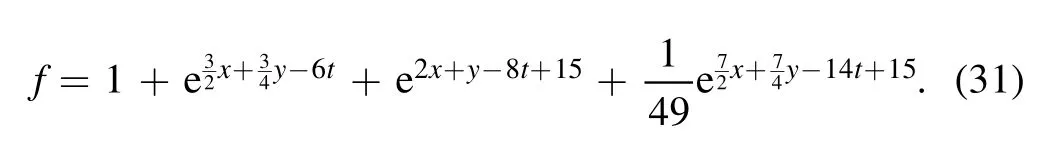
This soliton molecule structure of variable v of equation(17)for the(2+1)-dimensional KP-h system(3)is constructed by two line solitons in the molecule, which possess the same velocity,but their height and width are different (figure 2(a)).

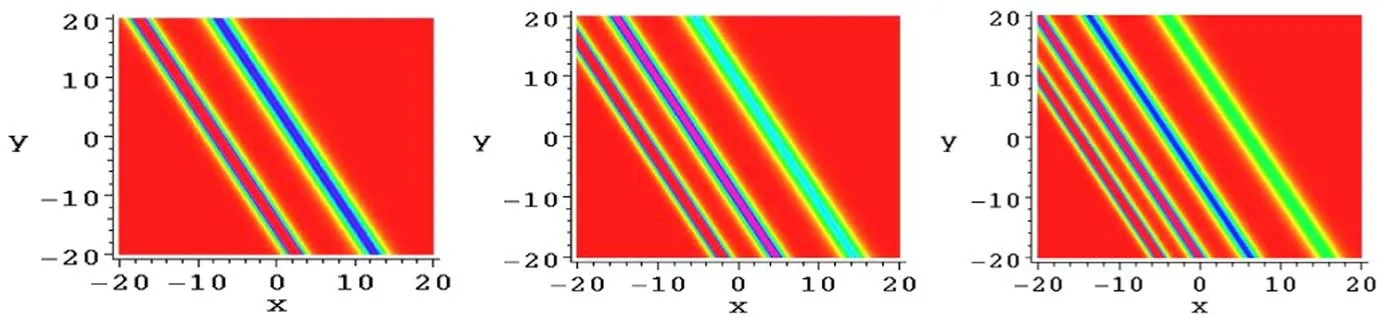
Figure 2.(a) The two-soliton molecule structure of the solution v from equations (17) and (31) at t=0.(b) The three-soliton molecule structure of the solution v from equations(17)and(33)at t=0.(c)The four-soliton molecule structure of the solution v from equations(17)and (35) at t=0.

· One three-soliton molecule

We continue to take the phase shift ai4=0(i ＜4) and ξ4=0 in equation (26), and require the velocity resonant condition (27) for i, j=1, 2, 3 the three-soliton molecule structure may appear.For example, when we set the parameters in equation (29) andwhile the others are derived as

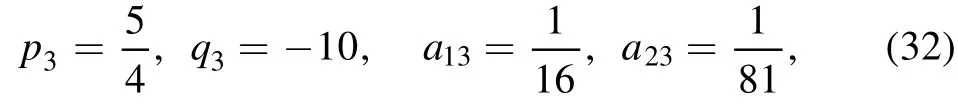
from equations (24), (25) and (27), then the transformation function f of equation (26) is given by

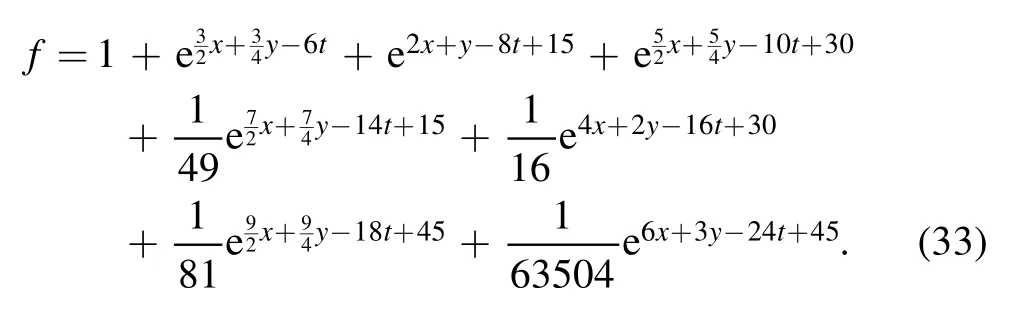
The three-soliton molecule structure of v for the (2+1)-dimensional KP-h system (3) is constructed directly from equations (17) and (33), where three line solitons in the molecule (figure 2(b)).

· One four-soliton molecule

When taking the phase shifts aij≠0(i ＜j,i,j=1,2,3,4)and the parameters qi≠0(i=1,2,3,4)in equation(26),and expanding the resonant conditions (27) for i, j=1,2,3,4, the four-soliton molecule can be produced.

For instance, we select the same parameters as equation (29) and

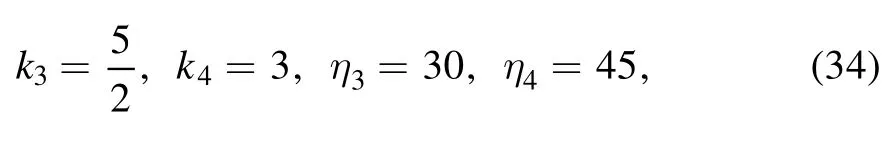
then the function f of equation (26) is derived as

For this purpose, after taking the long-wave limit

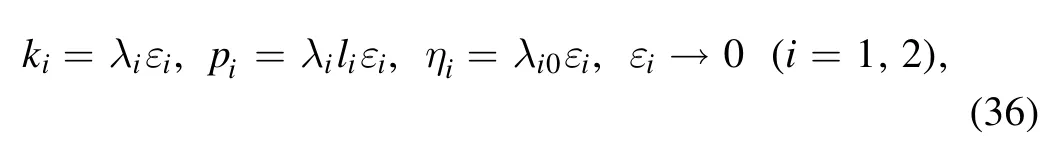
the transformation function f of equation (26) is simplified

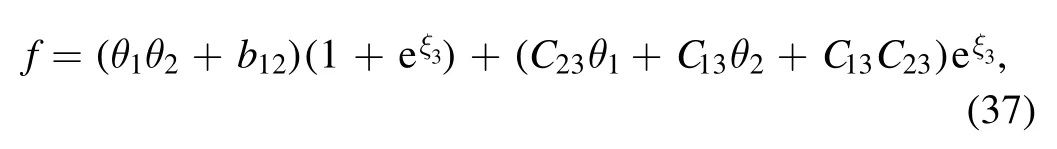
with the phase shift ai4=0(i ＜4) and ξ4=0.Here,

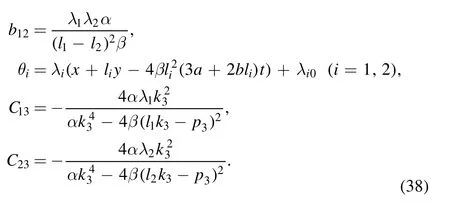
If we take the conjugate constants

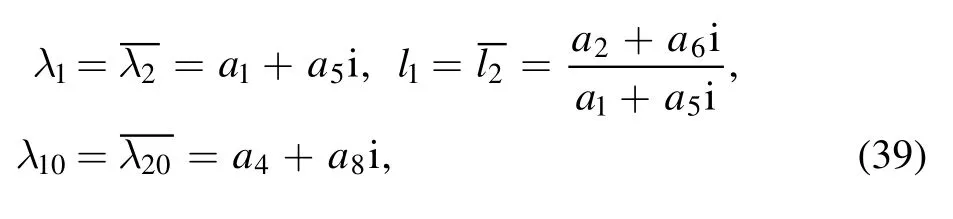
the supposing quadratic function

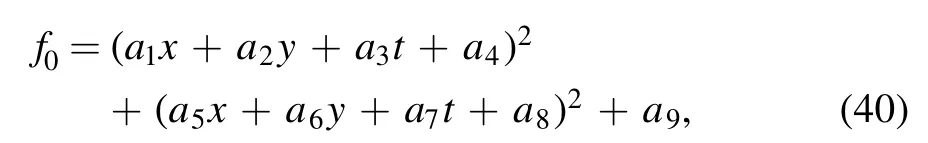
is derived from the expression f0≡θ1θ2+b12of equation (37) with the constraint relations of the parameters ai(1 ≤i ≤9) are

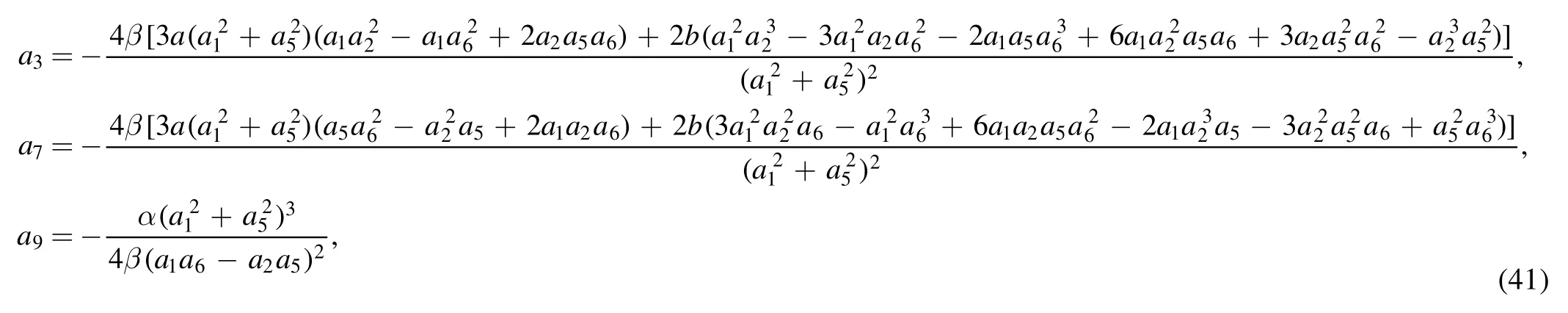
Therefore, the molecule with four line solitons is produced through equations (17) and (35) (figure 2(c)).

(2) The molecules constructed by the solitons and a lump

· The soliton molecule through a line soliton and a lump which the moving route of the lump is

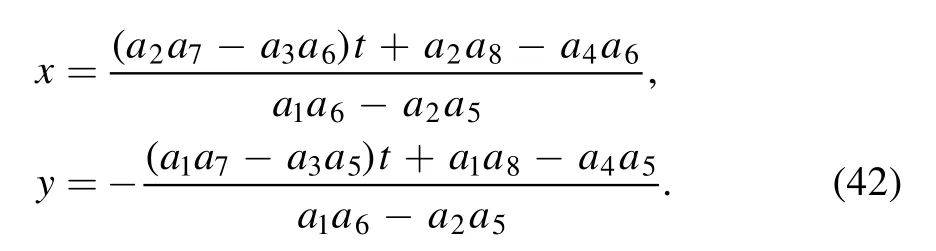
This solution may produce the soliton molecule through a line soliton and a lump with the condition

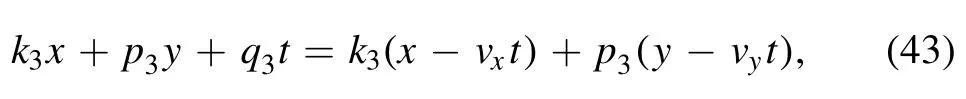
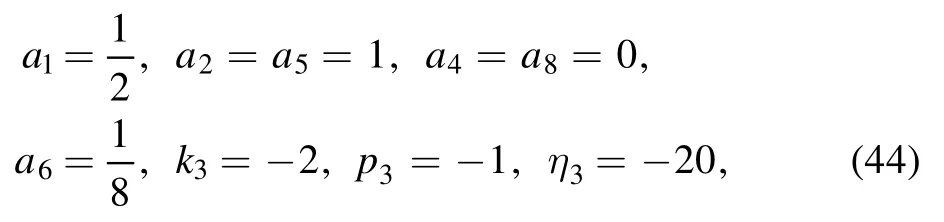
the transformation function f of equation (37) is

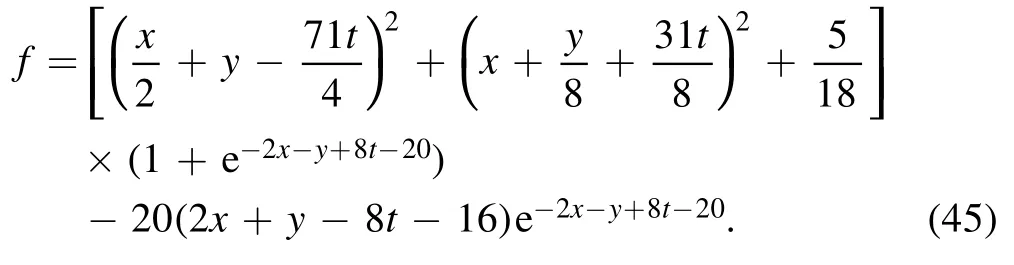
Figure 3 is one soliton molecule constructed through a line soliton and a lump at different times with the parameters are equation (44), while the moving velocity of this lump is

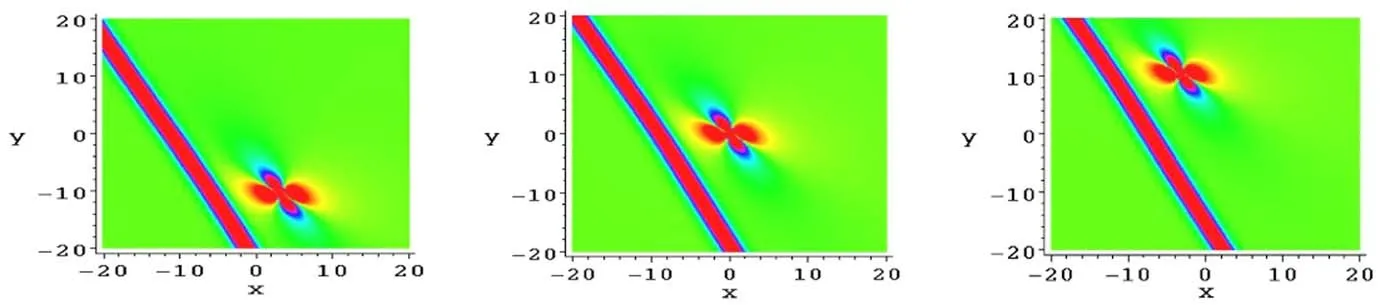
Figure 3.The soliton molecule consisting of a line soliton and a lump of the solution v from equations(17)and(45)at(a)t = -,(b)t=0 and (c) respectively.

· The soliton molecule t hrough the line soliton molecule and a lump

After taking the parameters aij≠0(i ＜j,i,j=1,2,3,4),qi≠0(i=1,2,3,4)of equation(26),and the long-wave limit condition of equation (36), the transformation function f of equation (37) is expanded

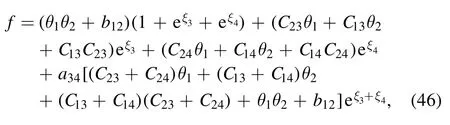
with

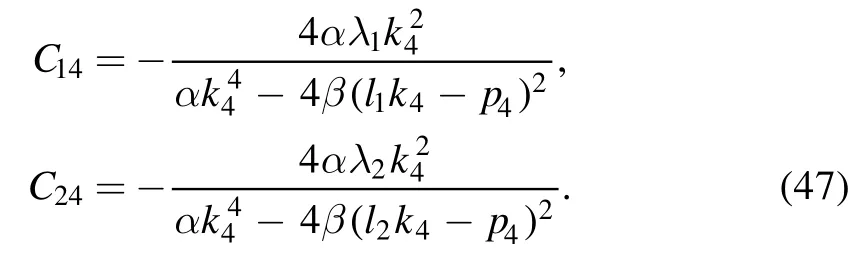
Through this auxiliary function, we can construct the soliton molecule structure of variable v of equation (17) for the (2+1)-dimensional KP-h system (3) by two line solitons and a lump in the molecule with the condition

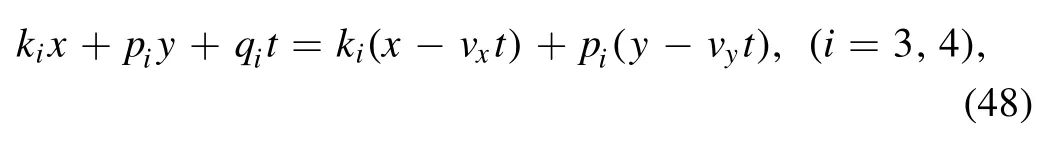
and

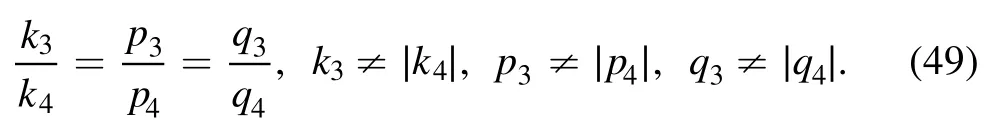
For example, after selecting the parameters a, b, α, β as equation (29) and

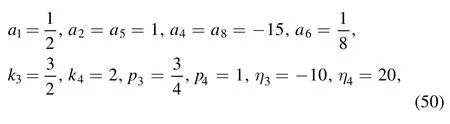
the transformation function f of equation (46) becomes

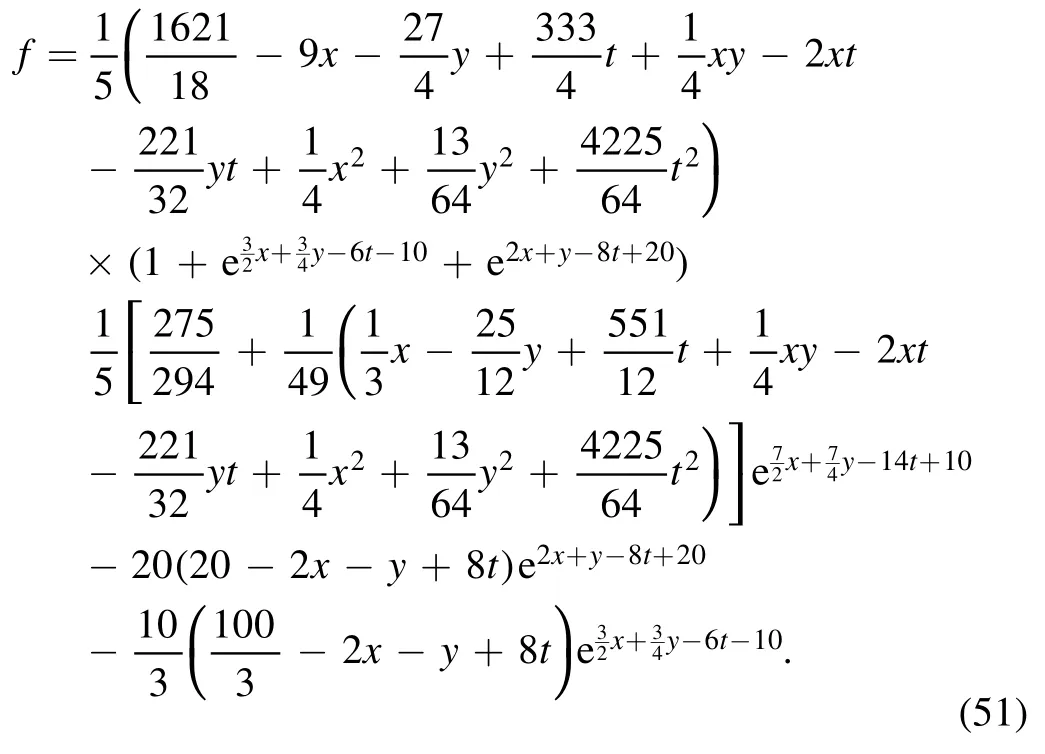
Figure 4 shows the soliton molecule through the line soliton molecule and a lump at different times with the parameters are taken as equation (50).

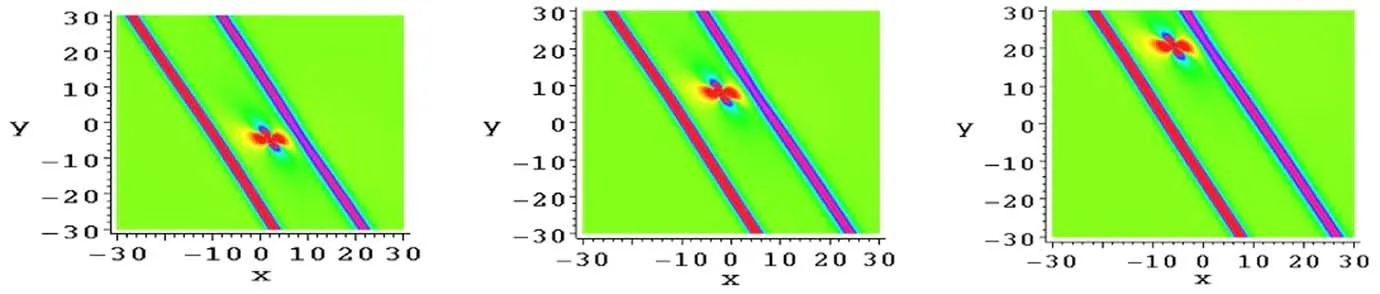
Figure 4.The soliton molecule consisting of the line soliton molecule and a lump of the solution v from equations (17) and (51) at (a)t = - (b) t=0 and (c)t = respectively.

However, if we don’t obey the rule of equation (48),but hold on equation (49), the above soliton molecule structure may be destroyed.For example, when taking the parameters a, b, α, β as equation (29), but

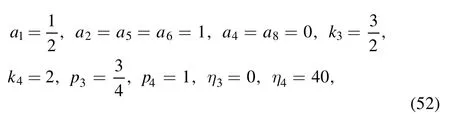
the function f of equation (46) is

This conclusion induces the elastic interaction of the line soliton molecule and a lump of the solution v from equations (17) and (53) for the (2+1)-dimensional KP-h system (3).Figure 5 shows that the amplitude, the velocity and the shape of these structures not any change front and back their collision.

Figure 5.The elastic interaction between the line soliton molecule and a lump of the solution v from equations(17)and(53)at(a)t=-2,(b)t=-1.3, (c) t=0 and (d) t=1, respectively.

(3) The molecules induced by the solitons and the breathers

· The soliton molecule through a line soliton and the breather

After taking the phase shift ai4=0(i ＜4) and ξ4=0 of equation (26), we let the conjugate relationξ1=ξ2[31, 32],i.e.the variables ki, piand ηi(i=1, 2) satisfy

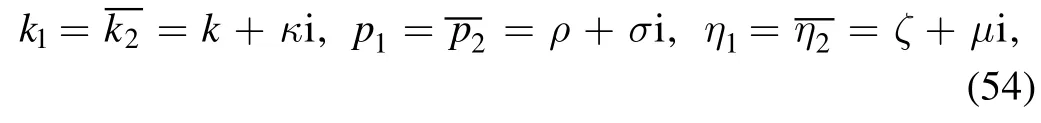
with i is an imaginary unit.Equation (26) is deduced

with

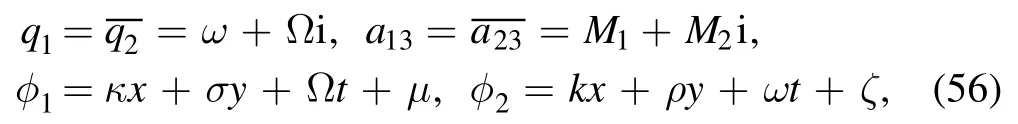
and ξ3, a12also obey equations (24), (25).

When taking the parameters a, b, α, β as equation (29),but

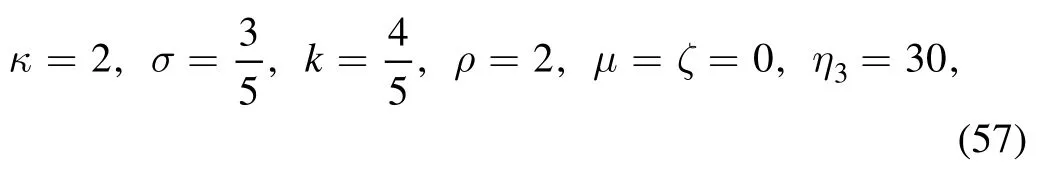
and

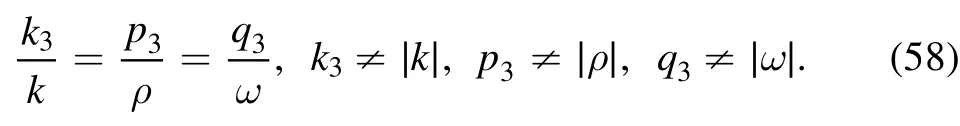
one can construct the soliton molecule expressed a line soliton and the breather of variable v of equation (17)for the (2+1)-dimensional KP-h system (3) through the function (55)(figure 6(a)).

Figure 6.(a) The soliton molecule expressed a line soliton and the breather for the variable v of equation (17) with the condition equations(55)–(58)at t=0.(b)The soliton molecule constructed the line soliton molecule and the breather for the variable v of equation(17)with the condition equations (61) and (62) at t=0.(c) The elastic interaction between the line soliton molecule and the breather with the condition equations(61)and(63)at t=0.(d)The soliton molecule formed through two breathers with the condition equations(68)and(69)at t=0.

· The soliton molecule through the line soliton molecule and the breather

When equations (54) and (56) hold with

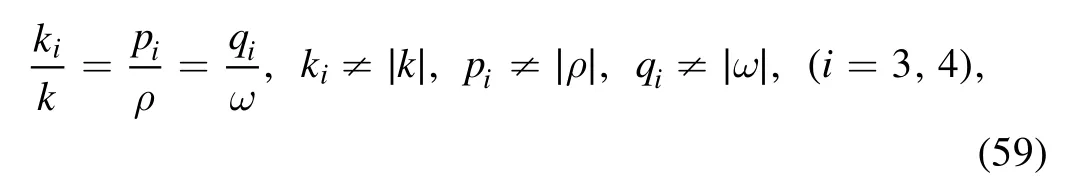
and

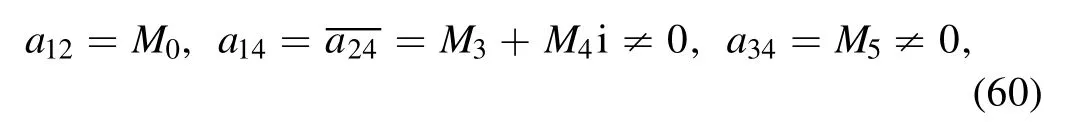
equation (26) is induced

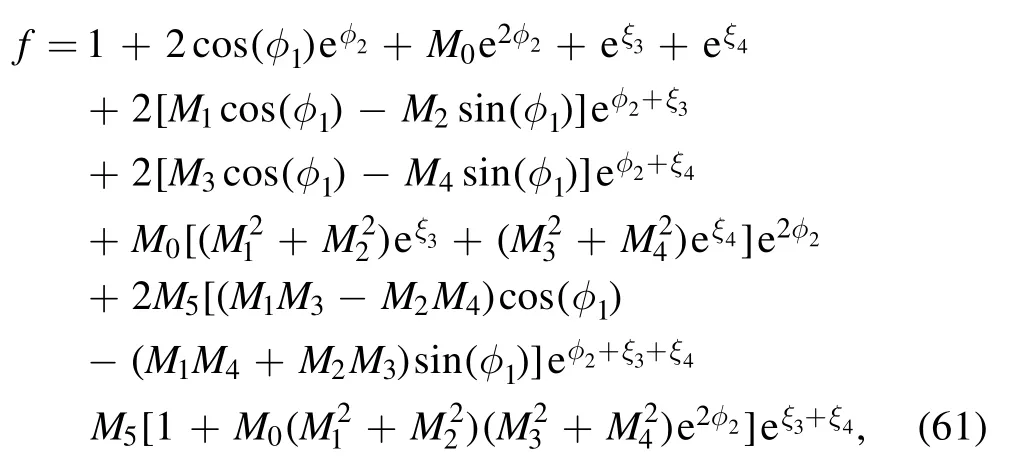
which is an expanded expression of equation (55).

Figure 6(b) shows the soliton molecule through the line soliton molecule and the breather at time t=0 with the parameters are selected as

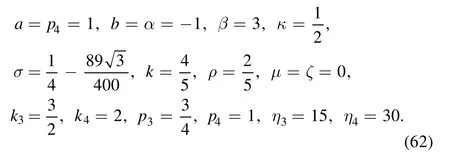
However,if we don’t obey the rule of equation(59),that is, when taking the parameters as equation (62) except for

the above soliton molecule structure may be destroyed.The interaction of the line soliton molecule and the breather is elastic for the (2+1)-dimensional KP-h system (figure 6(c)).

· The soliton molecule through two breathers

Based on equations (54) and (56), we further take

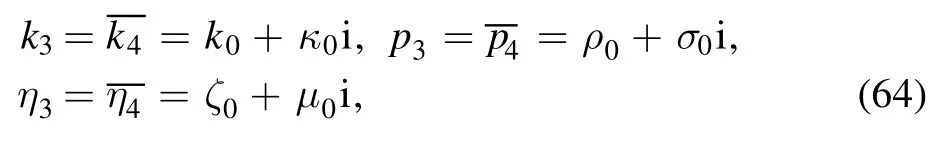
and

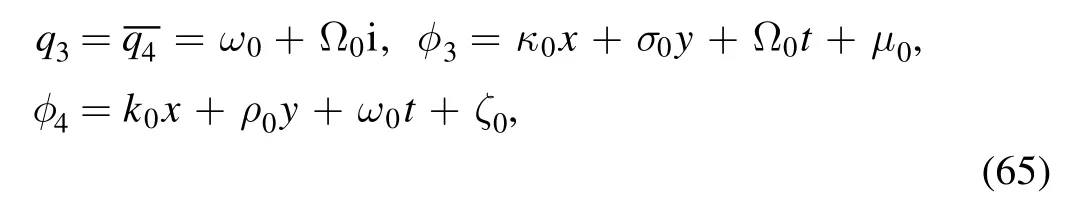
but

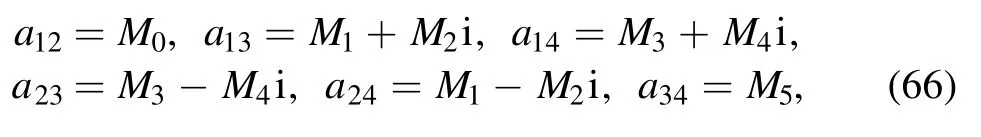
with

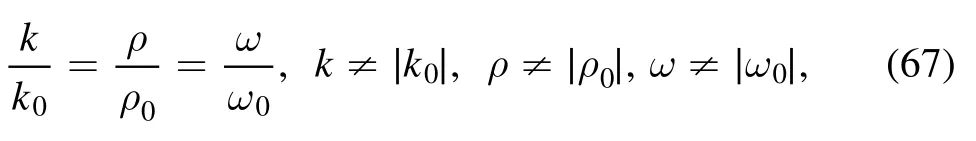
equation (26) is reproduced as

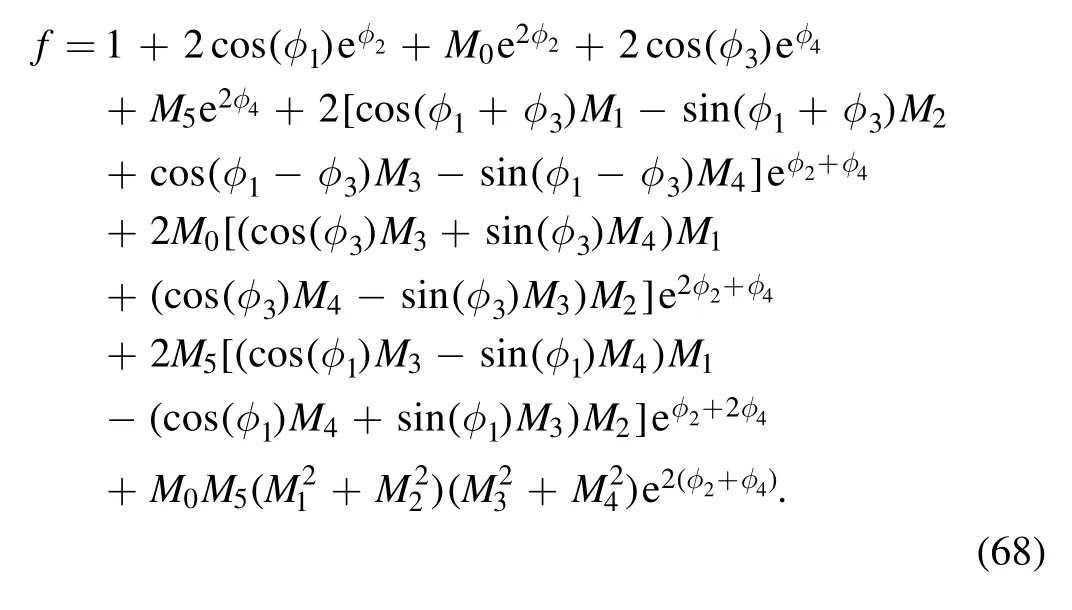
For this time,the soliton molecule occurs after taking the following parameters

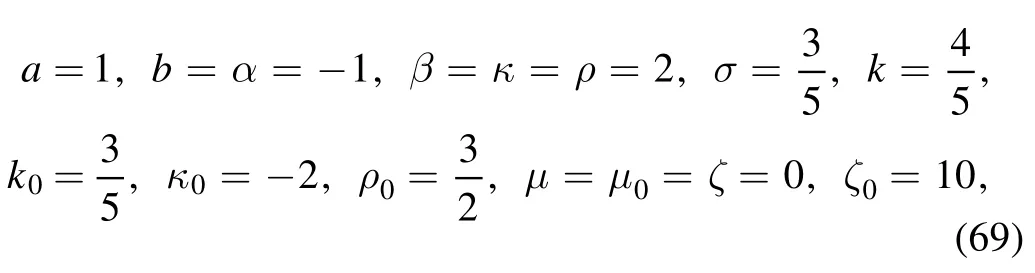
which is constructed by two breathers (figure 6(d)).

4.Summary

We employ the integrable KP-h system(3)as the investigated subject which is the (2+1)-dimensional KP equation (1)combining with the KP hierarchy (2).After taking the traveling wave transformation (7),the missing D’Alembert type solution (11) for this equation (3) is first derived.This solution contains several special Kink molecule structures (13)–(16).Further, after introducing the B?cklund transformation(17)and an auxiliary variable τ,the Hirota bilinear form(21)of equation (3) is conducted and the N-soliton solution (23)with equations (24) and (25) is presented.This N-soliton solution contains some typical soliton molecules including the line solitons, the breathers and a lump (figures 2–4, 6(a), (b)and (d)) as well as the elastic interaction between the line soliton molecule and a lump/the breather(figures 5 and 6(c))after selecting some special conditions and parameters.Up to now, these dynamics features have not been reported for this(2+1)-dimensional KP-h system (3).We believe that these structures derived above would be worth underlying in the future research.