Yusong Cao,Jian Wang,Yi Qiao,Junpeng Cao,3,4,?and Wen-Li Yang

1 Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2 School of Physical Sciences,University of Chinese Academy of Sciences,Beijing,China

3 Songshan Lake Materials Laboratory,Dongguan,Guangdong 523808,China

4 Peng Huanwu Center for Fundamental Theory,Xian 710127,China

5 Institute of Modern Physics,Northwest University,Xian 710127,China

6 Shaanxi Key Laboratory for Theoretical Physics Frontiers,Xian 710127,China

7 School of Physics,Northwest University,Xian 710127,China

Abstract We propose a method to construct new quantum integrable models.As an example,we construct an integrable anisotropic quantum spin chain which includes the nearest-neighbor,next-nearestneighbor and chiral three-spin couplings.It is shown that the boundary fields can enhance the anisotropy of the first and last bonds,and can induce the Dzyloshinsky–Moriya interactions along the z-direction at the boundaries.By using the algebraic Bethe ansatz,we obtain the exact solution of the system.The energy spectrum of the system and the associated Bethe ansatz equations are given explicitly.The method provided in this paper is universal and can be applied to constructing other exactly solvable models with certain interesting interactions.

Keywords:quantum spin chain,Bethe ansatz,Yang–Baxter equation,reflection equation

1.Introduction

Quantum integrable system is an important topic in the modern research of mathematical physics,theoretical physics and condensed matter physics[1,2].The corresponding exact solutions can supply the benchmarks for the new numerical simulation methods and new physical concepts.Bethe ansatz is one of the most powerful methods to obtain the exact solutions of one-dimensional quantum many-body problems[3,4].

The Heisenberg model is a typical quantum integrable system and has many applications in the theory of quantum magnetism and critical phenomena.By using the coordinate Bethe ansatz[5]or the quantum inverse scattering method[6–10],the Heisenberg model has been solved exactly.Based on the exact solutions,many interesting physical pictures such as the spinon and fractional charge have been found[11].The Heisenberg model includes the nearest neighbor(NN)spinexchanging interaction(i.e.theJ1–J2model[12]).Later,it was found that the next nearest neighbor(NNN)interaction in the strong correlated systems can also induce some new physics.Due to the competition between NN and NNN interactions,many novel magnetic ordered states and the Kosterlitz–Thouless-like quantum phase transitions arise in this kind of systems.We note that theJ1–J2model can not be solved by the Bethe ansatz.The chiral three-spin coupling is another typical spin-spin interaction which is used to describe the spin liquid phases in some low-dimensional systems[12–15].

The Yang–Baxter equation(YBE)plays a crucial role in the framework of Bethe ansatz[16,17].For the periodic boundary condition,the YBE can ensure the integrability of the system.While for the integrable open boundary conditions,besides the YBE,we also need the reflection equation,which can help us to prove the integrability and to obtain the exact solutions[18–20].Recently,the integrable open boundary problems have attracted a lot of attentions because they can provide the believable physical mechanisms such as boundary bound states,topological order,edge state,surface energy and helical spinon excitations[21–24].The corresponding results also have many important applications in modern theoretical physics such as open string theory[25]and non-equilibrium statistical physics[26,27].

In this paper,we propose an exactly solvable quantum spin chain which has the NN,NNN and chiral three-spin couplings with the open boundary condition.We find that due to the existence of boundary fields,the spins at boundaries are polarized.The boundary fields can enhance the anisotropy of NN spin-spin interactions of the first and last bonds.We also find that the boundary fields can induce the Dzyloshinsky–Moriya(DM)interactions[28–30]at the boundaries.The DM interaction could lead to some interesting elementary excitations.In this system,the boundary fields are parallel thus the U(1)symmetry is held.By means of the Bethe ansatz,we obtain the exact solution of the system.The energy spectrum and the associated Bethe ansatz equations(BAEs)are given explicitly.

The paper is organized as follows.The model Hamiltonian is explained and its integrability of the system is proved in section 2.In section 3,using the algebraic Bethe ansatz method,we construct the corresponding Bethe states and the corresponding eigenvalue of the transfer matrix.The associated BAEs are also given.Section 4 is attributed to the concluding remarks.

2.Integrable Hamiltonian

The exactly solvable model studied in this paper is described by the Hamiltonian

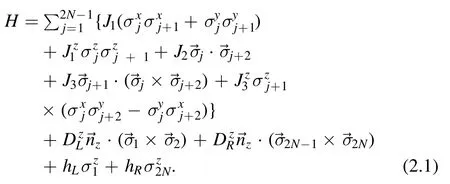
Let us explain the Hamiltonian(2.1)more clearly.The boundary condition of the system is the open one,which is achieved by adding two magnetic fields at the boundaries.We consider the case that two boundary fields are parallel.Choose the direction of magnetic fields as the z-direction and denote the strengths as

where a is the model parameter,η is the anisotropic parameter,ξ-andξ+are the boundary parameters quantifying the strengths of fields.Thus the boundary fields do not break the U(1)symmetry of the system.

Due to the existence of magnetic fields,the spins at the boundaries are polarized,which leads to the anisotropy of two boundary bonds are enhanced.Then the NN spin-exchanging interactions read

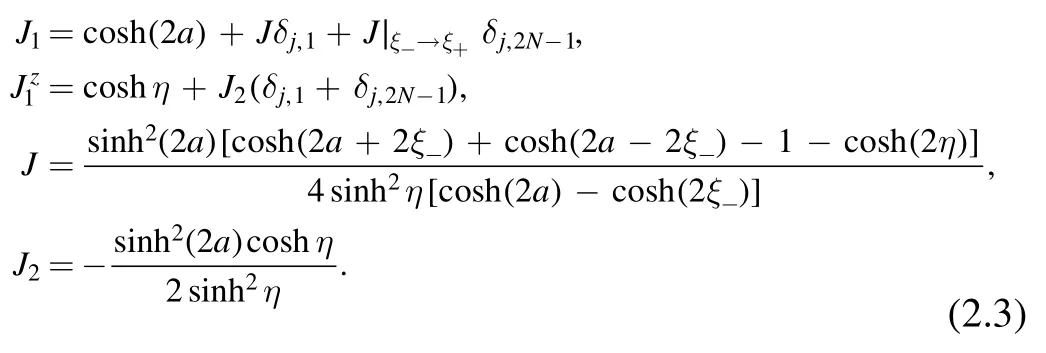
From above equation,we see that the NN couplings in the bulk keep unchanged except for the two boundary bonds.Meanwhile,because the NNN interactions are involved,the boundary fields can also induce the DM interactions of two boundary bonds along the z-direction and the corresponding strengths are

The integrability of the system requires that the NNN spin-exchanging is isotropic and the strength is measured by J2.The chiral three-spin couplings are anisotropic and the corresponding strengths are

It is clear that the chiral three-spin interactions are the staggered ones.Please note that the conventionhas been used.The Hermitian of Hamiltonian(2.1)requires that a is real if η,ξ+andξ-are pure imaginary,while a is pure imaginary if η,ξ+andξ-are real.

Next,we should show how to construct the integrable Hamiltonian(2.1).The integrability of the system is related with following R-matrix

where u is the spectral parameter.The R-matrix(2.6)is defined in the direct product spacesV0?Vjand has properties

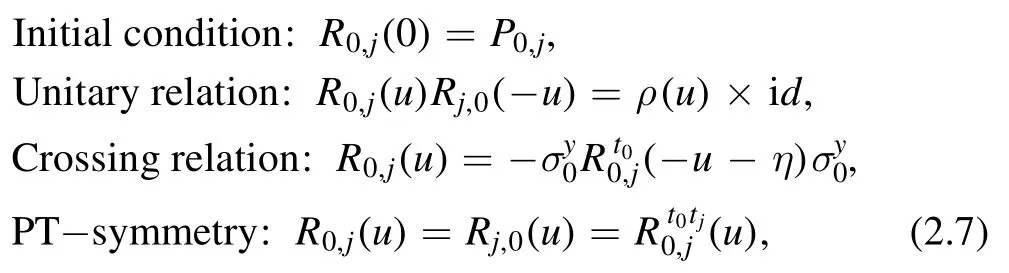
whereρ(u)=-sinh(u+η)sinh(u-η)sinh-2ηandP1,2is the permutation operator possessing the propertyR1,2(u)=P0,1R0,2(u)P0,1.The R-matrix(2.6)also satisfies the YBE

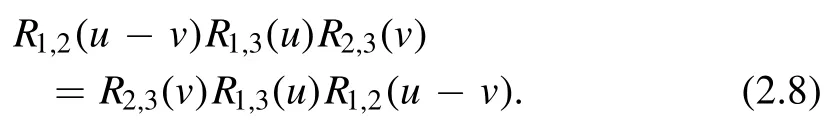
Because we consider the integrable open boundary condition,we should introduce the reflection matrixK-(u)at one side[20,31–33]

which satisfies the reflection equation

The boundary magnetic field at the other side is quantified by the dual reflection matrixK+(u)with the form of

which satisfies the dual reflection equation

Starting from R-matrix(2.6),we construct the single-row monodromy matrixT0(u)and the refelcting oneas

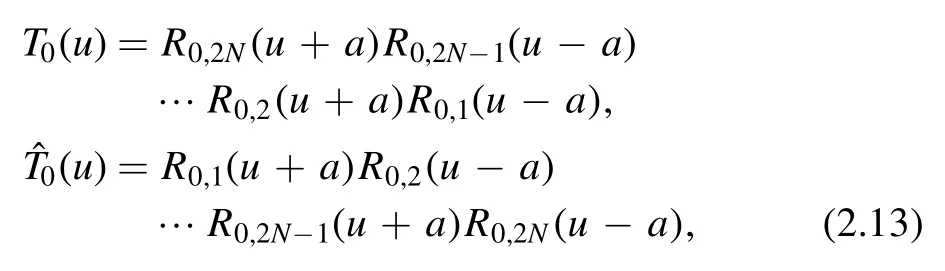
where the subscript 0 means the auxiliary space and the subscripts{1,2,…,2N}denote the physical or quantum spaces.From the reflection matrix and the single-row monodromy matrices,we defnie the double-row monodromy matrixU0(u)as

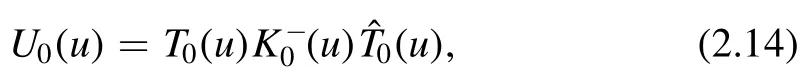
which satisfies the reflection equation

By using the dual reflection matrix and the double-row monodromy matrix,we obtain the transfer matrix of the system

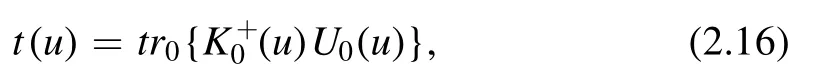
where tr0means the partial trace in the auxiliary space.With the help of crossing symmetry(2.7),we can prove that the transfer matrix t(u)has the crossing relation

From the YBE(2.8),reflection equation(2.10)and the dual one(2.12),we find that the transfer matrices with different spectral parameter commutate with each other,i.e.

Thus the transfer matrix t(u)can generate all the conversed quantities and the system is integrable.The Hamiltonian(2.1)is generated from the transfer matrix t(u)as

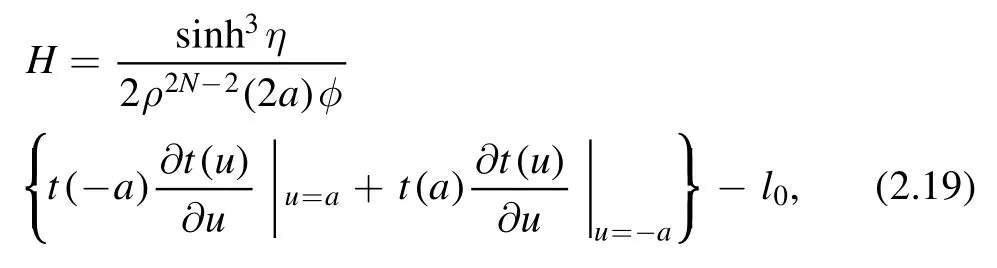
where φ and l0are the constants with the definitions

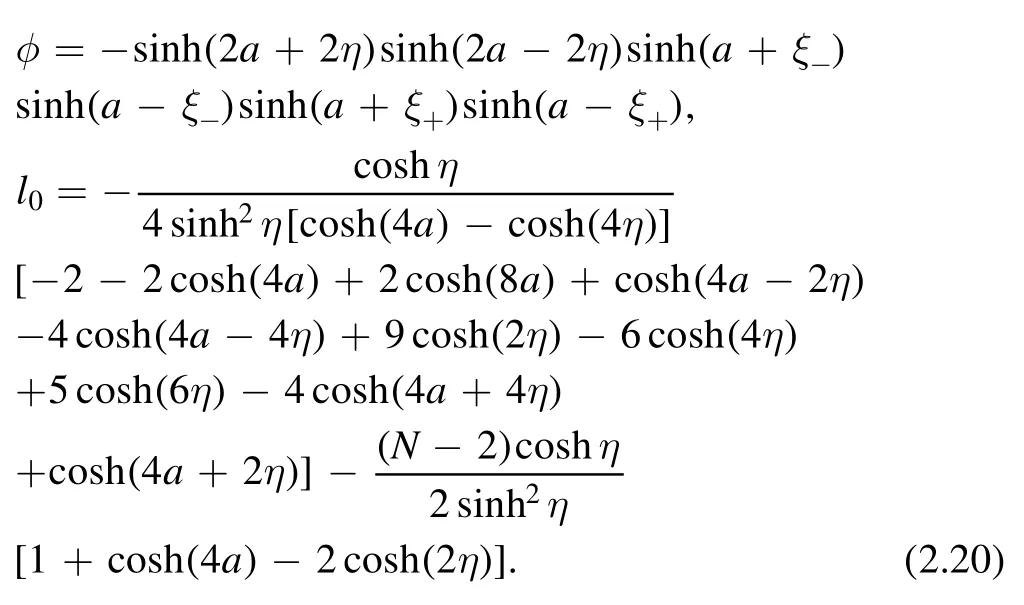
3.Exact solution

Now,we solve the Hamiltonian(2.1)by using the algebraic Bethe ansatz.The matrix form of single-row monodromy matrixT0(u)in the auxiliary space is

where A(u),B(u),C(u)and D(u)are the operators defined in the quantum spaces.From the crossing symmetry(2.7),the reflection single-row monodromy matrix reads

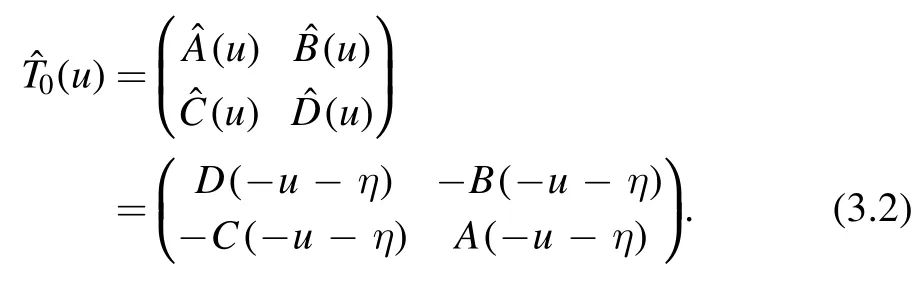
Then we arrive at the matrix form of double-row monodromy matrixU0(u)

One afternoon, a little boy had lost his puppy1. He looked under his bed. He looked all over his house. But still there was no puppy. Finally, he looked for his puppy in the garden. After a few hours, he still could not find the puppy.

We choose the vacuum state of the system(2.1)as

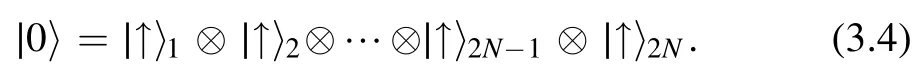
The elements of monodromy matrixT0(u)acting on the vacuum state give

From the YBE(2.8),we can prove that the following relation holds

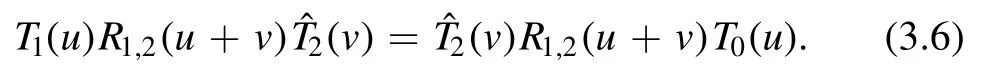
Based on it,we obtain the commutative relation

By using equations(3.2),(3.5)and(3.7),we obtain the results of elements of double-row monodromy matrixU0(u)acting on the vacuum state

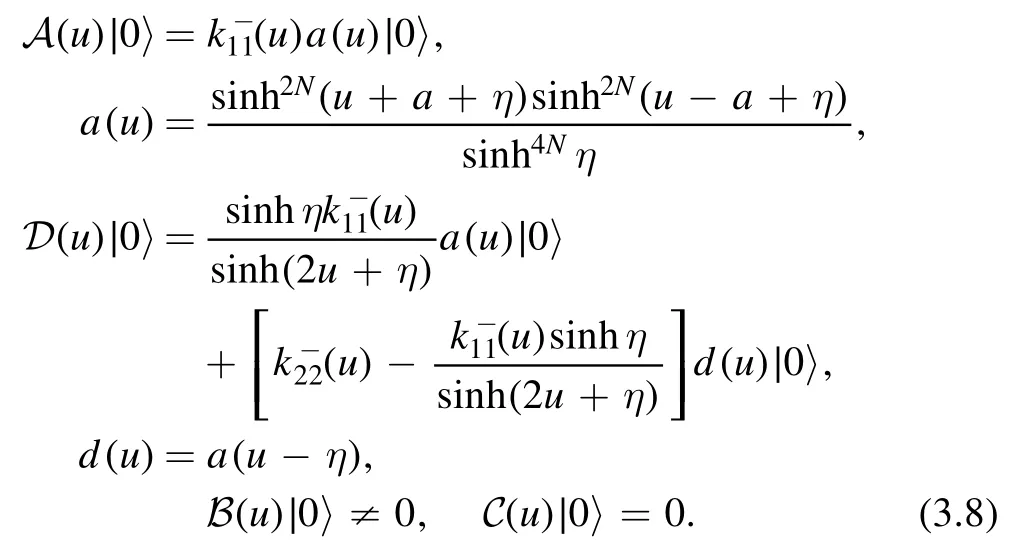
We see that the vacuum state is the eigenstate of operators A(u)and D(u).The operator C(u)acting on the vacuum gives zero and the operator B(u)acting on the vacuum state generates other states thus can be regarded as the creation operator of eigenstates of the system.Assume the eigenstates are

where{μj∣j=1,2,…,M}are the Bethe roots which will be determined later.

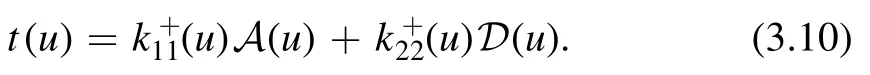
If we define

the transfer matrix is rewritten as

Next,we should act the transfer matrix t(u)on the assumed eigenstates(3.9).In order to obtain the detailed results,it is clear that we should exchange the orders betweenand B(μj).From the reflection equation(2.15),we have

Repeatedly using above commutative relations,we obtain

where

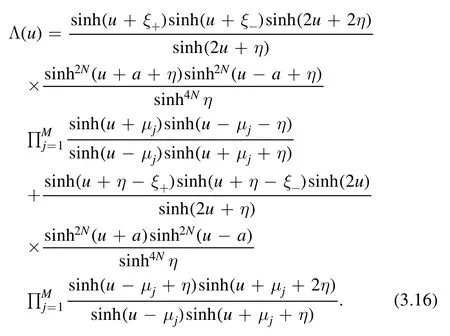
If all the unwanted terms are zero,which gives that the Bethe roots{μj∣j=1,…,M}must satisfy following BAEs,

Table 1.Numerical solutions of the BAEs(3.17),where2N=4,η=0.6,a=1.3i,ξ+=0.3,ξ-=1.8,n indicates the number of energy levels and En is the corresponding energy.The energy En calculated from the Bethe roots is exactly the same as that obtained from the exact diagonalization of the Hamiltonian(2.1).

the assumed states(3.9)indeed are the eigenstates of the transfer matrix t(u).Because the system only has the U(1)symmetry,the number of Bethe roots could beM=1,2,…,2N.

According to(2.19),we obtain the eigenvalue of Hamiltonian(2.1)

where the Bethe roots must satisfy the BAEs(3.17).

Next,we check above analytical results numerically.We first solve the BAEs(3.17)and obtain the values of Bethe roots.Substituting these values into(3.18),we obtain the eigenenergies of the Hamiltonian(2.1).The results are listed in table 1.After that,we numerically diagonalize the Hamiltonian(2.1)with same model parameters.We find that the eigenenergies of the Hamiltonian(2.1)obtained by solving the BAEs(3.17)are exactly the same as those obtained by the exact diagonalization.Meanwhile,the expression(3.18)gives the complete spectrum of the system.

4.Conclusion

In this paper,we propose a method to construct new quantum integrable models.As an example,we construct an anisotropic quantum spin chain which includes the NN,NNN and chiral three-spin couplings with open boundary condition.We find that the boundary fields can enhance the anisotropy of boundary NN coupling bonds.Meanwhile,the boundary field can also induce a polarized boundary DM interaction along the z-direction.By using the algebraic Bethe ansatz,we obtain the exact solution of the system.The energy spectrum and the BAEs are give explicitly.We note that this method is universal and can be used to construct other integrable models with certain interesting interactions.

The boundary fields considered in this work are parallel.If the boundary fields are unparallel and do not break the integrability,which means that the reflection matrices(2.9)and(2.11)have non-diagonal elements,then the spins of quasi-particles may change after the boundary reflecting.Therefore,the total numbers of quasiparticles with fixed spincomponents are not conserved.The U(1)symmetry of the system is broken and the algebraic Bethe ansatz does not work,because(3.4)is no longer the correct vacuum state.If the boundary fields satisfy some constraints[21,22],we can use the generalized Bethe ansatz just like that has done for the XYZ spin chain[7].For the most generic integrable nondiagonal boundary reflections,the corresponding system may be solved by the off-diagonal Bethe ansatz[34–36].Moreover,the unparallel boundary fields can induce the completely anisotropic DM interactions at boundaries,then some novel magnetic ordered states such as the helical spinon excitations may arise.

Acknowledgments

We would like to thank Prof Y Wang for his valuable discussions and continuous encouragement.The financial supports from National Program for Basic Research of MOST(Grant Nos.2016 YFA0300600 and 2016YFA0302104),National Natural Science Foundation of China(Grant Nos.12 074 410,12 047 502,11 934 015,11 975 183,11 947 301 and 11 774 397),Major Basic Research Program of Natural Science of Shaanxi Province(Grant No.2017ZDJC-32),Australian Research Council(Grant No.DP 190 101 529),the Strategic Priority Research Program of the Chinese Academy of Sciences(Grant No.XDB33000000),the fellowship of China Postdoctoral Science Foundation(Grant No.2020M680724),and Double First-Class University Construction Project of Northwest University are gratefully acknowledged.

ORCID iDs