Yu-Hang Sun(孫宇航) and Yu-Xia Xie(謝玉霞)

School of Science,Xi’an University of Posts and Telecommunications,Xi’an 710121,China

Keywords: quantum coherence,entanglement,twisted boundary conditions

1. Introduction

Quantum spin systems provide the natural playground for studying nontrivial physical phenomena in many-body physics. Traditionally,these phenomena were studied by calculating various thermal quantities such as the entropy, magnetization, magnetic susceptibility, and specific heat.[1]With the development of quantum information science, a variety of quantum correlations have also been proven to be efficient tools to study quantum characters of a system in a physically meaningful and mathematically rigorous fashion. Among them, entanglement which was first noted in 1935[2]and experienced rapid development in the past few decades, has been extensively investigated.[3]Some more general quantum correlations, such as quantum discord[4]and measurementinduced nonlocality,[5-7]also provide intriguing perspectives for understanding quantumness of a many-body system.[8]

While quantum correlations describe quantum characters of the bipartite or multipartite states, there is a more fundamental notion called quantum coherence. It stems from the superposition principle of the basis states and characterizes quantumness of a single-partite system. Although it has been perceived earlier than those of different quantum correlations, a rigorous framework for quantifying coherence was formulated only in 2014.[9]It is the resource theory of coherence, within which a variety of coherence measures were proposed in the past few years.[9-17]Inspired by these coherence measures, researches focused on the evolution[18-25]and freezing[26-29]of coherence, as well as its fundamental properties,[30-33]operational interpretation,[34-39]and role in quantum information tasks,[40-45]have been carried out.Moreover, quantum coherence in various spin-chain models was analyzed in Refs.[46-51]using these measures.

When considering the multipartite systems, coherence is also helpful in interpreting quantum correlations such as entanglement[10,16,52]and quantum discord.[53-57]In particular,an operational connection between steered coherence(SC)and nonlocal quantum resources(e.g.,entanglement[58,59]and Bell nonlocality[60]) has been revealed. When the spin-chain systems are considered,the control of SC has been studied in Refs.[61-64],and the role of SC in detecting quantum phase transitions can be found in Ref.[65]. Different from the previous works, in this work we investigate the HeisenbergXXmodel with a twisted boundary. We will show that both the SC and entanglement for thermal equilibrium states of this model can be significantly enhanced by tuning the twist angleθto an optimal value.

This paper is organized as follows. In Section 2 we recall how to measure the SC and entanglement. In Section 3 we introduce the physical model. In Section 4, the SC and entanglement for thermal states of the considered model with varying twist angle are analyzed. Finally,Section 5 is devoted to a summary of the main finding of this paper.

2. Measures of the SC and entanglement

To start with, we recall in short how to measure the amount of SC in the bipartite states. As such a measure is based on the resource theory of coherence,we first review two extensively used measures of coherence.[9]The first one is thel1norm of coherence defined by‖ρ-δ‖l1minimized over allδ ∈?, whereρis the state of interest and?represents the set of incoherent states. In the reference basis{|i〉},it can be obtained as[9]

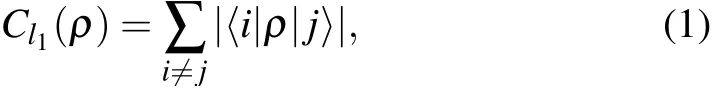
which is just the sum of the absolute values of the off-diagonal elements ofρ. The second one is the relative entropy of coherence defined byS(ρ‖δ)minimized over allδ ∈?,and can be obtained analytically as[9]

whereρdiagrepresents the density operator obtained by deleting all the off-diagonal elements ofρ, andS(ρ) =-tr(ρlog2ρ)is the von Neumann entropy ofρ.

Based on these coherence measures, one can introduce the SC for a two-qubit stateρAB. It was defined by first performing the local measurementsΠ±i=(I±σi)/2 (σ1,2,3are the standard Pauli operators)on qubitAand then calculate the average coherence of the collapsed states for qubitB.Depending on the framework adopted, the SC can be defined in two different manners. The first one is given by[58]

whereH2(···) denotes the binary Shannon entropy function,andC(ρAB)is the concurrence given by[69]

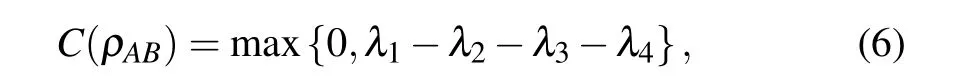
withλi’s being the square roots of the eigenvalues of the product matrixR=ρAB(σ2?σ2)ρ*AB(σ2?σ2) arranged in nonincreasing order.

3. The Heisenberg XX model

We consider the HeisenbergXXmodel with twisted boundary conditions. The corresponding Hamiltonian is given by

that is,the third spin interacts with the first spin after rotating an angleθalong thez-axis clockwise.Clearly,Eq.(8)reduces to the usual periodic boundary conditions whenθ=0 and to the anti-periodic boundary conditions whenθ=π.

For this model, the thermal equilibrium state at temperatureTcan be described by the density operatorρ(T) =Z-1e-?H/kBT, withZ=tr(e-?H/kBT) being the partition function andkBis Boltzman’s constant. By virtue of the eigenvalues{εi}and the eigenstates{|ψi〉}of ?H,ρ(T)can be written explicitly as

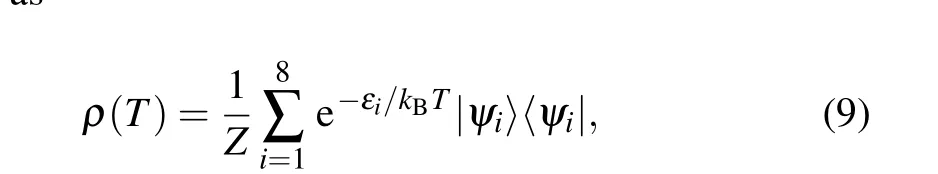
where the partition functionZ=∑ie-εi/kBT.

Because the form of ?His complicated, it is difficult to derive{εi}and{|ψi〉}analytically,hence in the following we solve them numerically. As we consider in this paper the SC and the pairwise entanglement,we further derive the reduced density operatorρij(T)=trk ρ(T), which is in the following form:

where the matrix elementsa,b,andcare the same for differentρi j, whilezijare different for differentρij, but their absolute values are also the same.All these elements can be determined

hence we always haveEf(ρ12)=Ef(ρ13).

In the following, we will assumeJ=1 andkB=1, i.e.,all our subsequent discussions are in units ofJandkB.

4. Improving SC and entanglement by tuning the twist angle

Based on the above preliminaries, we start to study how the twist angleθand the transverse magnetic fieldBaffect the SC and entanglement in theXXmodel. Because it can be directly obtained from Eq.(7)that both ?Cscα(ρi j)andEf(ρij)are symmetric with respect toB=0 andθ=π, we present only those results forB≥0 andθ ∈[0,π]. In fact, entanglement in the cyclicXX[72]andXXXchains[73,74]have been studied. Moreover, by assuming the topological boundary conditions,entanglement and quantum discord in the HeisenbergXXZchain[75]and nonlocal advantage of quantum coherence in the HeisenbergXXXchain[63]have also been studied recently.

4.1. The steered coherence

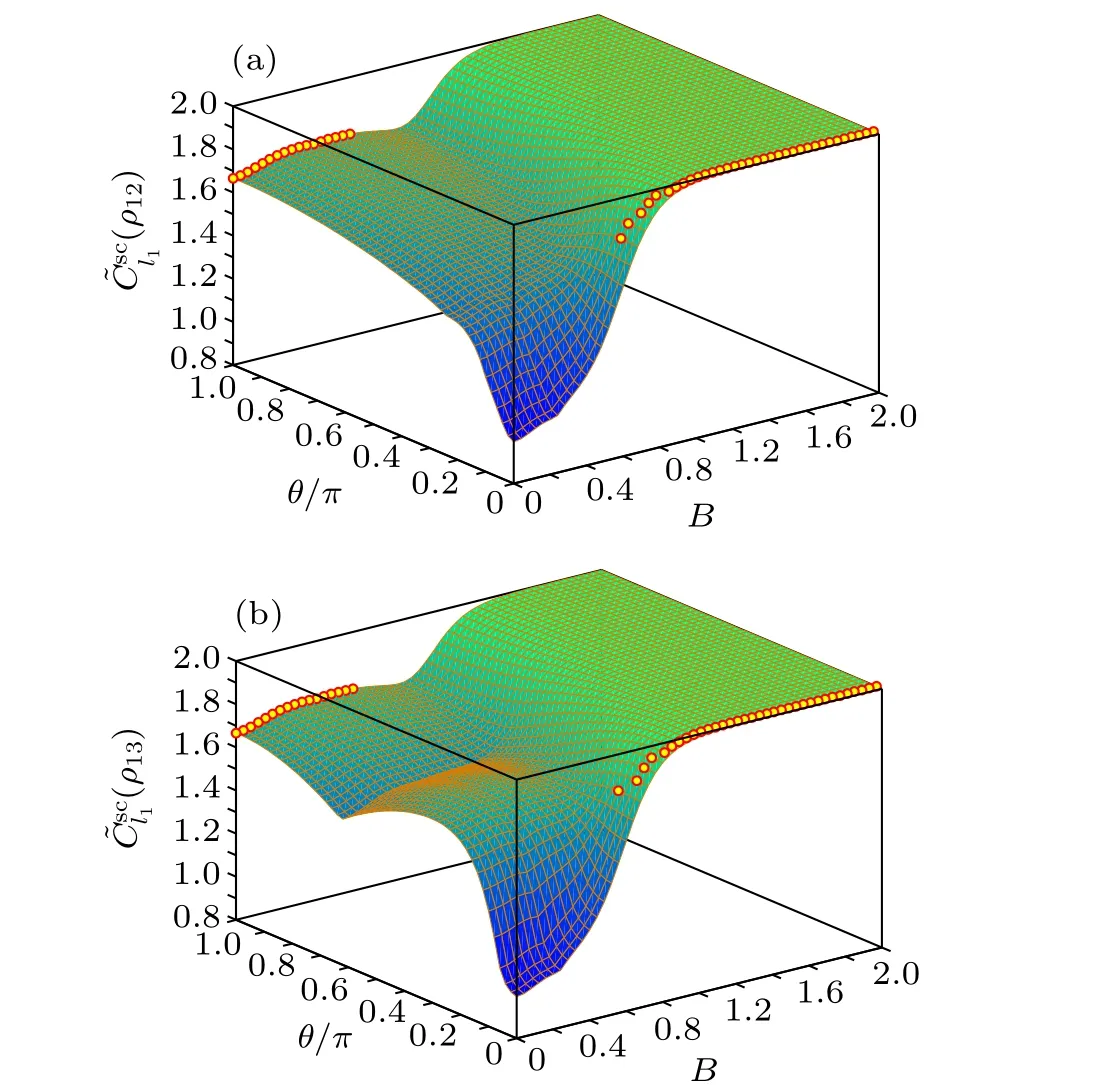
Fig.1.(ρ12)and(ρ13)versusB and θ/πfor theHeisenbergXXmodel with T =0.1. Thecirclesdenote the critical points at whichthe corresponding SC takes its maximum.

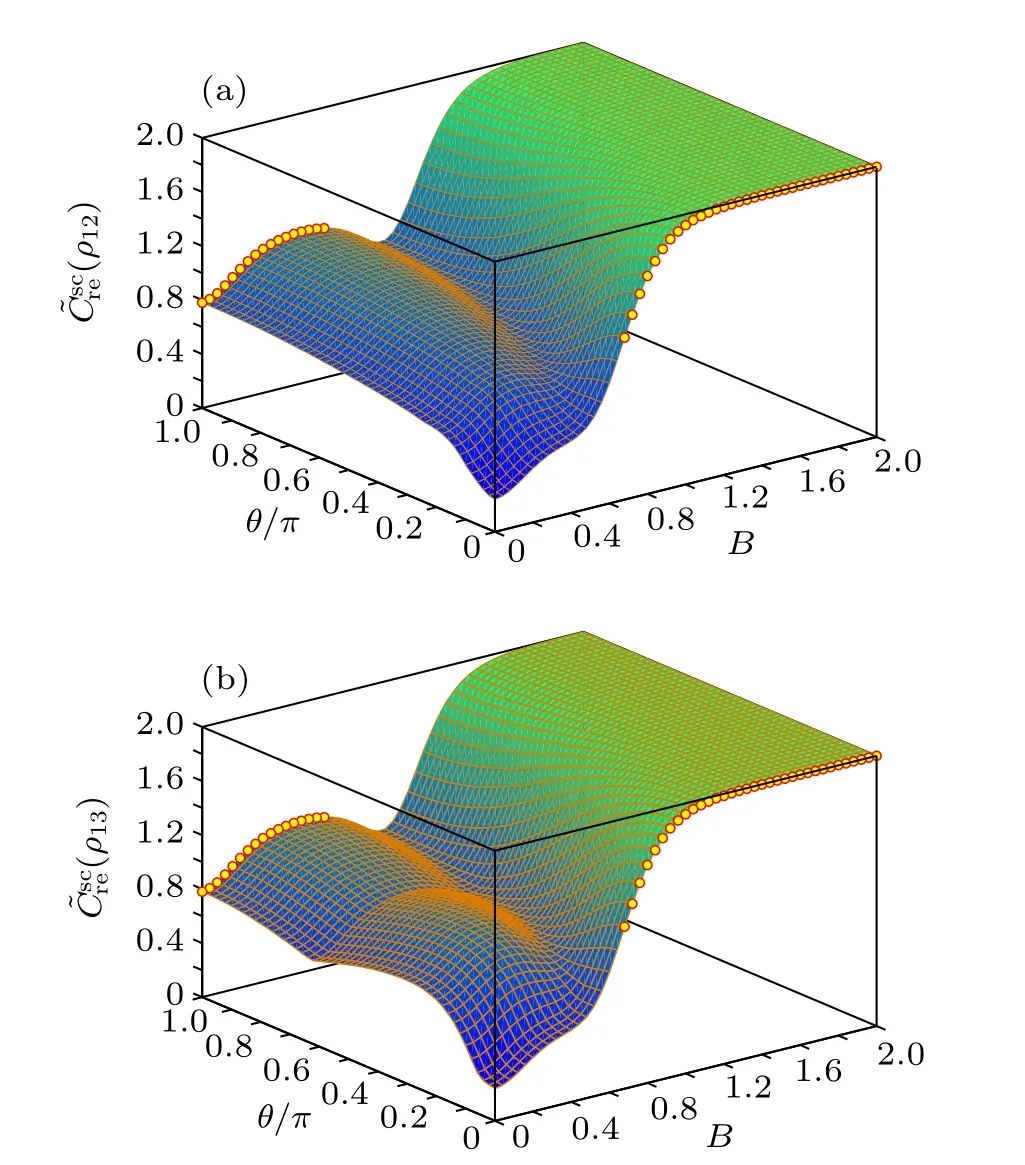
Fig.2. C?rsec(ρ12)and C?rsec(ρ13)versus B and θ/π for the Heisenberg XX model with T =0.1. The circles denote the critical points at which the corresponding SC takes its maximum.

From the above analysis, one can see that the SC can be noticeably enhanced by tuning the twist angleθof the boundary spins. Physically, such an enhancement is due to the change of the energy level structure of the system as twisting the boundary spins breaks the translational invariance of ?H, and the form of{εi}and{|ψi〉}will be changed. Such a change will affect the SC of each|ψi〉and their probabilities inρ(T), thus results in the improvement of the SC ofρ(T)for specific twist angle. Forθ=0 andπ, one can derive analytically{εi}and{|ψi〉}of ?Hand show directly that the SC ofρ(T)withθ=πis larger than that withθ=0 in the weak field region, whereas the opposite case occurs in the strong field region.

In Fig.3,we show the temperature dependence of the critical magnetic fieldBc,α(ρi j)below which the optimal twist angleθopt=π. When considering thel1norm of SC,Bc,l1(ρij)’s for different spin pairs are different. They both increase rapidly with an increase in the temperatureT, and whenT?0.782,their values become very large. For the relative entropy of SC,however,Bc,re(ρi j)is independent of the different spin pairs,and it increases smoothly with the increase ofT. In particular,in the high temperature region,Bc,re(ρi j)increases nearly linearly with the increase ofT(e.g.,by using the numerical data obtained in the region ofT ∈[0.8,2.0],their relation can be fitted approximately asBc,re(ρi j)≈1.501T+0.1822).The physical origin of the difference betweenBc,l1andBc,reis the difference between thel1norm of coherence and the relative entropy of coherence which are at the root of the SC given in Eq.(4),asCl1(ρ)contains only the magnitude information of the off-diagonal elements of a density operatorρ, whileCre(ρ)contains both the magnitude and phase information of all the elements ofρ,see Eqs.(1)and(2).

Finally, we give a short analysis on how the transverse magnetic fieldBaffects the SC.In the low temperature region,one can see from Figs. 1 and 2 that both the measures of SC can be noticeably enhanced when the magnetic field is strong enough, although they may experience slight decrease in the intermediate region ofB. In the high temperature region (we do not list the plots here for conciseness of this paper),the SC increases gradually with the increasingB,that is,the presence of the transverse magnetic field is beneficial for enhancing the SC between any two spins.

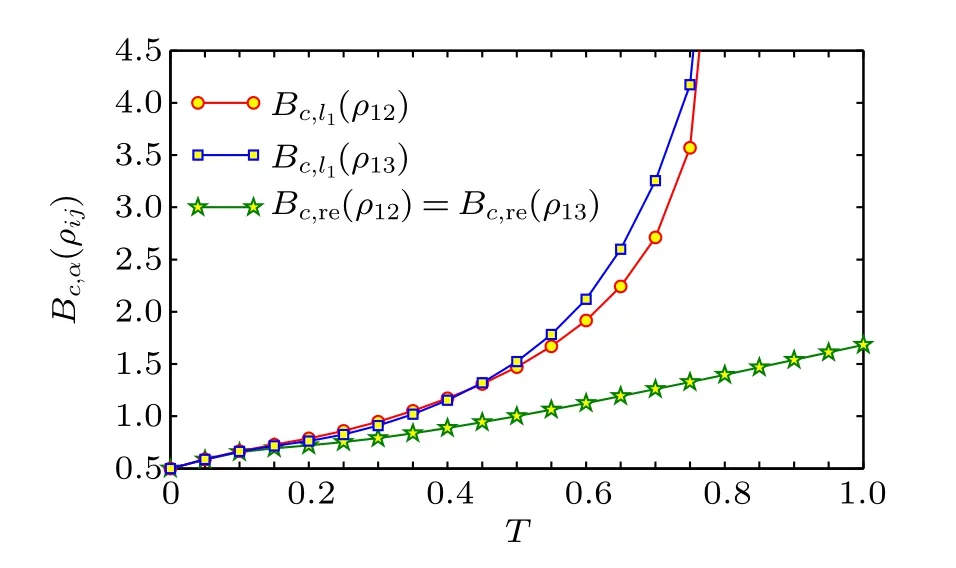
Fig. 3. The critical Bc,α(ρij) below which θopt =π versus T for the Heisenberg XX model. When T ?0.782,both Bc,l1(ρ12)and Bc,l1(ρ13)will be very large and the figure is cut to better visual for the temperature dependence of Bc,re(ρ12).

4.2. The pairwise entanglement

In this subsection,we investigate how the pairwise entanglement is affected by tuning the twist angle of the HeisenbergXXchain. As pointed out in Section 3, we always haveEf(ρ12)=Ef(ρ13), so Fig. 4 only shows the dependence ofEf(ρ12)onBandθ/π,from which one can observe that it exhibits different behaviors from those of the SC.Firstly,Ef(ρ12)always increases monotonically with the increase ofθand takes its maximum atθopt=π. This indicates that the HeisenbergXXmodel with anti-periodic boundary conditions is beneficial for creating entanglement. Secondly,one can see from Fig.4 that for fixed twist angleθ,Ef(ρ12)first increases with the increase ofBand reaches its maximum at a critical magnetic fieldBc,E, after which it turns out to be decreased gradually. A further numerical calculation shows that whenθincreases from 0 toπwith fixedT=0.1,Bc,Efirst decreases from the value of about 0.398 to 0.379 and then increases monotonically to 0.622.

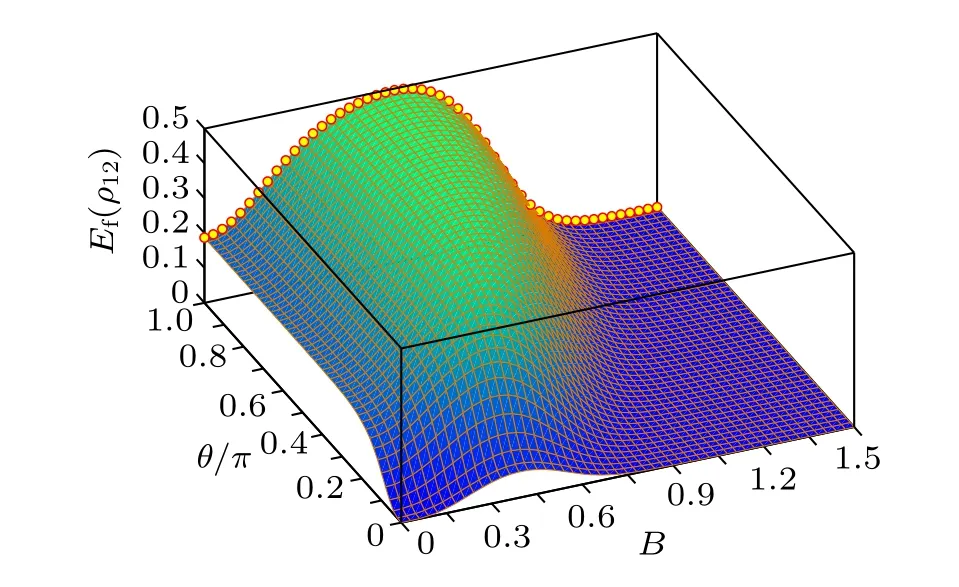
Fig. 4. Ef(ρ12) versus B and θ/π for the Heisenberg XX model with T =0.1. The circles denote critical points at which Ef(ρ12) takes its maximum.

By increasing the temperatureT, the pairwise entanglement may undergo sudden death in the whole parameter region of (B,θ). In Fig. 5, we show the dependence of the critical temperatureTcabove which the pairwise entanglement disappears onθ/πin the weak field region (the entanglement is infinitesimal in the strong field region even when the temperatureTis very low,therefore it is meaningless to consider it).From this figure one can see thatTcincreases with an increase inθ. This implies that the temperature region in which the entanglement exists can also be enhanced by increasing the twist angle,and the anti-periodic boundary conditions(i.e.,θ=π)is the most suitable boundary conditions both for creating pairwise entanglement and for extending temperature region of non-vanishing entanglement.

Fig.5.The critical temperature Tc above which Ef(ρ12)=0 versus θ/π for the Heisenberg XX model with different B.

5. Summary

To summarize, we have examined SC and entanglement for thermal states of a three-spinXXmodel under twisted boundary conditions.Different from the previous works which focused on the periodic boundary conditions,our results show that both the SC and the entanglement can be noticeably enhanced by tuning the twist angleθ. For thel1norm of SC,the optimal twist angleθoptequalsπin the weak field region and decreases fromπto 0 with an increase in the strength of the magnetic field, while for the relative entropy of SC,θopt=πin the weak field region andθopt=0 otherwise.As for the entanglement of any two spins,it increases monotonically when the twist angle increases from 0 toπand therefore we always haveθopt=πfor this case. Moreover,the critical temperatureTcabove which the entanglement vanishes can also be noticeably enhanced by increasing the twist angle. These show evidently that the twist angle can serve as an efficient parameter for tuning the SC and entanglement in the spin-chain systems. As the SC characterizes the ability of one party to control the coherence of another party by local operations and classical communication,the present results may be useful in coherence-based quantum information processing tasks such as the remote preparation of coherent states.