(School of Mathematics and Physics,Anhui University of Technology,Maanshan 243032,China)

Abstract:Let RCS be a semidualizing(R,S)-bimodule.Then RCS induces an equivalent between the Auslander class AC(S)and the Bass class BC(R).Let A and B be free normalizing extensions of R and S respectively.In this paper,we prove that HomS(BBS,RCS)is a semidualizing(A,B)-bimodule under some suitable conditions,and so HomS(BBS,RCS)induces an equivalence between the Auslander class and the Bass class Furthermore,under a suitable condition onRCS,we develop a generalized Morita theory for Auslander categories.

Keywords:Semidualizing module;Auslander class;Excellent extension

§1.Introduction

LetRbe a ring.Mod-Rdenotes the category of all rightR-modules,andR-Moddenotes the category of all leftR-modules.

Over a commutative,noetherian local ring,semidualizing modules provide a common generalization of a dualizing module and a free module of rank one.Foxby[6]first defined them(PG-modules of rank one).In[8],Henric Holm and Diana White extended the definition of semidualizing(S,R)-bimodules,whereRandSare arbitrary associative rings,which are defined as follows:An(R,S)-moduleRCSis semidualizing if

(a1)RCadmits a degreewise finiteR-projective resolution(i.e.,there exists a resolution···→P1→P0→M→0 where eachPiis finitely generatedR-projective).

(a2)CSadmits a degreewise finiteSop-projective resolution.

(b1)The natural homothety mapRRR→HomSop(C,C)is an isomorphism.

(b2)The natural homothety mapSSS→HomR(C,C)is an isomorphism.

A semidualizing module over a commutative noetherian ring gives rise two full subcategories of the category ofR-modules,namely the so-called Auslander classAC(R)and Bass classBC(R)defined by Avramov and Foxby[1,6].Semidualizing modules and their Auslander(resp.,Bass)classes have caught the attention of several authors,see for example[1–7].Henric Holm and Diana White also extended the definitions of Auslander classes and Bass classes to non-commutative non-noetherian rings.The Auslander classAC(S)is defined as follows:theAuslander class with respect to C,denoted byACorAC(S),consists of allS-modulesMsatisfying

(c)The natural mapμCCM:M→HomR(C,C?R M)is an isomorphism.

We will writeμM=μCCMif there is no confusion.Dually,we can defineBC(R).

LetRbe commutative and noetherian.Christensen[2]proved that ifψ:R→Sis local and flat,thenCis semidualizing forRif and only ifC?R Sis semidualizing forS.This result is the motivation for our Theorem 2.1.LetSbe a ring and letRbe a subring ofS(with the same 1).Sis called a finite normalizing extension ofRif there exist elementsa1,a2,...an∈Ssuch thatS=aiRwhereaiR=Raifori=1,2,...n.Finite normalizing extensions have been studied in many papers such as[9–15].Sis called a free normalizing extension ofRifS=aiRis a normalizing extension ofRandSis free with basis{a1=1,a2,...,an}as both a rightR-module and a leftR-module.

LetAandBbe the free normalizing extensions ofRandSrespectively.LetSCRbe a semidualizing(R,S)-bimodule.We get the semidualizing(A,B)-bimodule with respect toRCS.Under a suitable condition onRCS,we develop a generalized Morita theory for Auslander categories.

§2.Auslander categories and free normalizing extensions

In this section,we will give our main results.

Theorem 2.1.Let A=Rai and B=Sbj be left and right free normalizing extensionsof R and S respectively,where each ai centralizes the elements of R and bj centralizes theelements of S.Suppose rijkc=csijk for all c∈C and all i,j,k;where put aiaj=rijhahand bibj=sijhbh.

(1)If RCS is a bimodule,SEndR(RCS)and R～=EndS(RCS),then

as ring isomorphism.

(2)If RCS is a semidualizing(R,S)-bimodule,then Hom(B,RCS)is a semidualizing(A,B)-bimodule,and

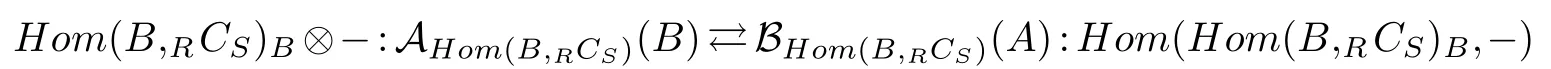
defines an equivalent.

Proof.(1)See[16],Theorem 1.1.

(2)First,we shall show thatAHom(BBS,RCS)admits a degreewise finiteA-projective resolution.AsR-modules we haveHom(BBS,RCS).ThenHom(BBS,RCS)has a degreewise finiteR-projective resolution

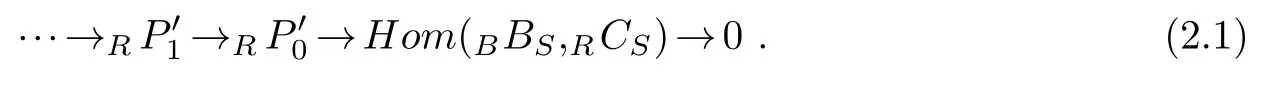
ApplyingAAR?R-to(2.1),we get

where eachAARR P′iis a finitely generated projectiveA-module for alli=0,1,2,···.By(1),Hom(BBS,RCS)is also anA-module.So we define the map

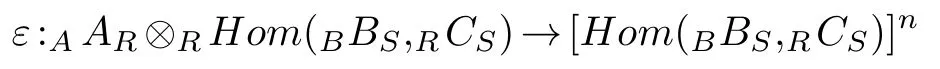
byε(a?f)(b)=Clearlyεis anA-module isomorphism.ThenAHom(BBS,RCS)has a degreewiseA-projective resolution.Similarly,ifRCShas a degreewise finiteS-projective resolution,thenHom(BBS,RCS)has a degreewise finiteB-projective resolution.

Next,we shall show that

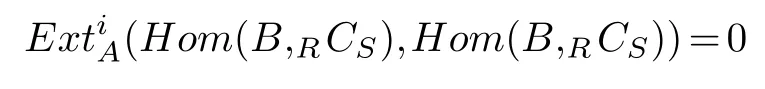
and

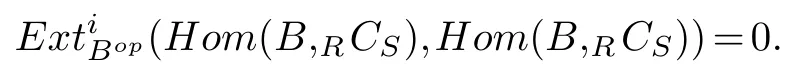
We only show(Hom(B,RCS),Hom(B,RCS))=0.In fact,everyA-module isRmodule,thus(M,N)=0 implies(M,N)=0.We have

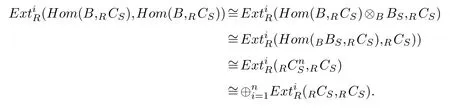
Then(Hom(BBS,RCS),Hom(BBS,RCS))=0.Hom(BBS,RCS)is a semidualizing(A,B)-bimodule and

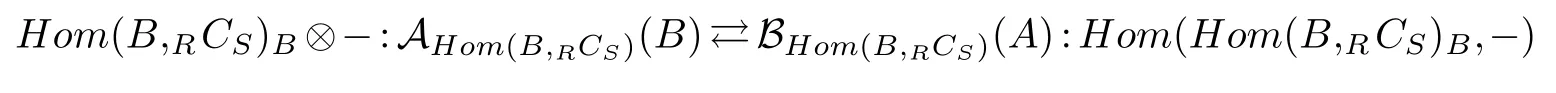
defines an equivalent by[8].

Corollary 2.1.Let A=Rai be a free normalizing extension of R,where each ai centralizesthe elements of R.Suppose rijkc=crijk for all c∈C and all i,j,k;where put aiaj=.

If RCR is a semidualizing(R,R)-bimodule,then Hom(A,C)is a semidualizing(A,A)-bimodule,and the following holds for an A-module F:

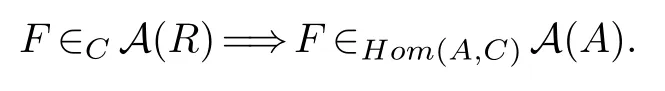
In the rest of this section,we shall discuss generalized Auslander classes and extension rings.

Definition 2.1.Let RCS be an(R,S)(RCS).Define

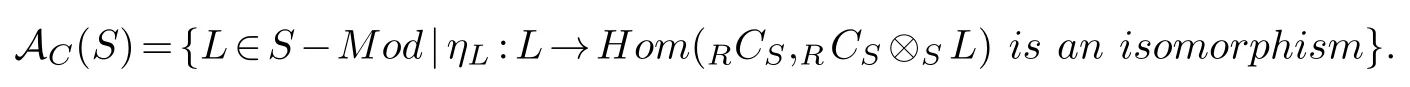
Let RCS be an(R,S)-bimodule,and S～=EndR(RCS).Define

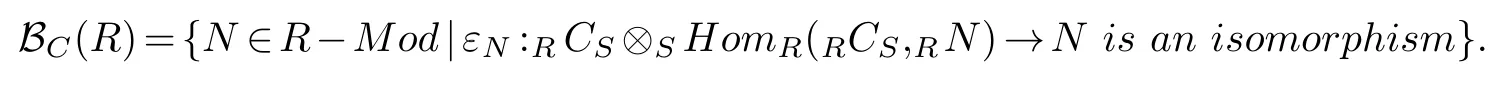
Proposition 2.1.Let RCS be an(R,S)-bimodule with R～=HomS(RCS,RCS)(RCS).

Then RCS?-:AC(S)BC(R):Hom(RCS,-)defines an equivalence.

Theorem 2.2.(1)Let RCS be a finitely generated projective S-module,and REndS(RCS).

Then we have the following adjoint equivalence of categories

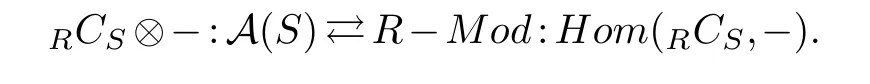
(2)Let RCS be a finitely generated projective S-module,and SEndR(RCS).Then we have the following adjoint equivalence of categories

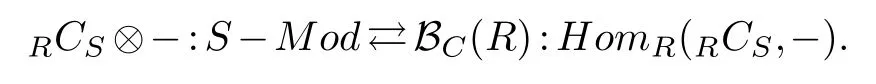
Proof.(1)We begin by observing that for anyR-moduleM,the moduleHom(RCS,RM)in fact is an object ofAC(S).Note that,

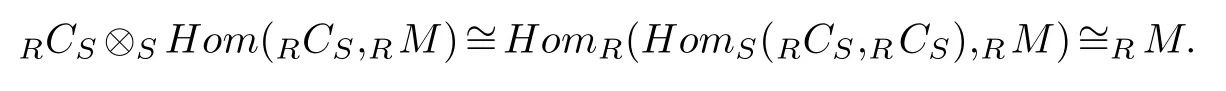
Thus,

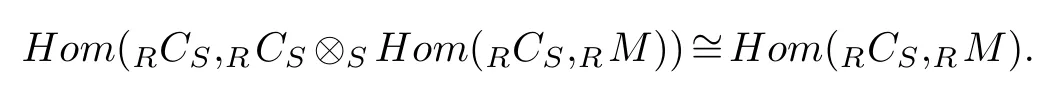
We now need to show that the adjoint pair is an equivalence ifRNR-Mod.SinceRCS?S Hom(RCS,RM),the adjoint pair is an equivalence.

(2)Similar to the proof of(1).

Remark 2.1.Theorem 2.2 is a variant of Morita theory.If CS is a finitely generated projective generator and REndS(CS),we have that the category of R-modules is equivalent to the category of S-modules over S.Theorem 2.2 states that if CS is a finitely generated projective module,then the category of R-modules is equivalent to the subcategory AC(S)of S-modules.

Proposition 2.2.Let A=Rai and B=Sbj be left and right free normalizingextensions of R and S respectively,where each ai centralizes the elements of R and bj centralizesthe elements of S.Suppose rijkc=csijk for all c∈C and all i,j,k;where put aiaj=and bibj=

(1)Let RCS be a finitely generated projective Sop-module,and R～=End(RCS).Then wehave the following adjoint equivalence:

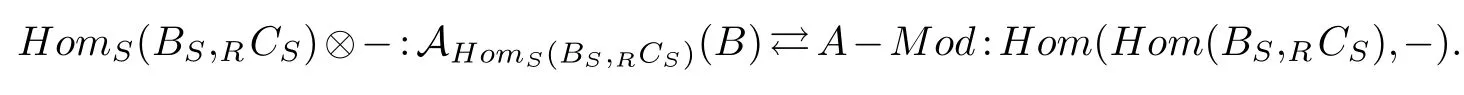
(2)Let RCS be a finitely generated projective Sop-module,and S～=End(RCS).Then we have the following adjoint equivalence:

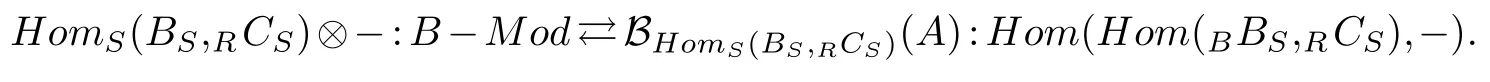
Proof.Note that the proofs of(1)and(2)are similar,so we only show(1).SinceRCSis a finitely generated projectiveS-module,Hom(BBS,RCS)is a finitely generated projectiveB-module.By Theorem 2.1(1),

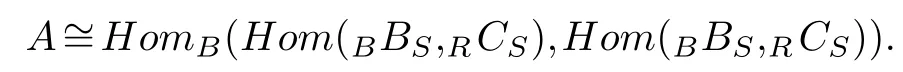
Thus,Hom(BBS,RCS)defines an equivalence by Theorem 2.2.

Acknowledgements

We are greatly indebted to the anonymous referee for helpful comments and stimulating hints.