廣東省東莞市第四高級中學(523220) 王文濤

函數(shù)y= ex在x= 0 處的泰勒展開式(即麥克勞林公式)為ex=1+x++Rn(x),其中Rn(x)為泰勒展示的余項.受此啟發(fā),我們可以得到一系列高中生可以證明的不等式.

引理1當x≥0,n ∈N*,ex≥1+x+

證明欲證ex≥ 1 +x+只需證

設(shè)f(x)=則

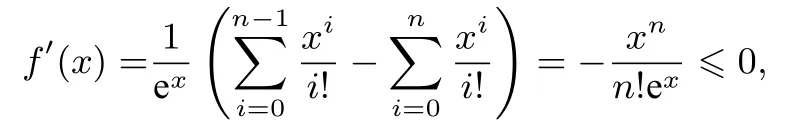
所以f(x)在[0,+∞)上是減函數(shù).f(x)≤f(x)max=f(0)=1,所以

題目(2020年高考全國Ⅰ卷理科第21 題) 已知函數(shù)f(x)=ex+ax2-x,

(1)當a=1 時,討論f(x)的單調(diào)性;

(2)當x≥0 時,f(x)≥+1,求a的取值范圍.

首先,我們考慮上述高考題的一個推廣形式.

推廣1當x≥0,n ∈N*時,1+x+≤ex,求a的取值范圍.

解當n= 1 時, 欲a+x≤ex, 只需a≤ex -x.設(shè)g(x) = ex - x(x≥0).注意到g′(x) = ex -1 ≥0, 則g(x)min=g(0)=1,所以a≤g(x)min=1.

下面考慮n≥2 的情形.當x= 0 時,a ∈R.當x ＞0時,

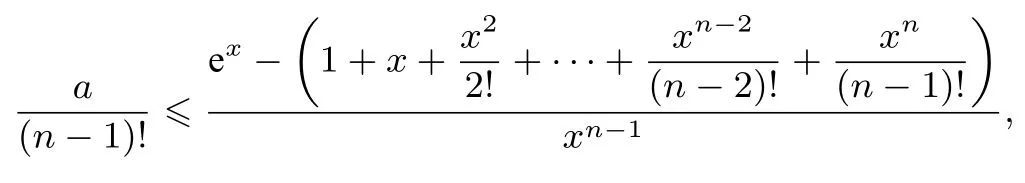
因為

所以

由引理1 知,當x ＞0 時,ex-＞0,所以當x ∈(0,n-1)時,f′(x)＜0;當x ∈(n-1,+∞)時,f′(x)＞0.所以f(x)min=f(n-1).

簡評易見, 2020年高考全國Ⅰ卷理科第21 題的第二問無非是推廣1 中取n= 3 的特殊情形.實際上, 由整理得1+x+≤ex,由推廣1的結(jié)論知-2a≤所以a≥

推廣1 給出一個普適性的結(jié)果,盡管推導過程看起來較為復雜,但是,重要的是思想方法,而不是公式本身.借助于推廣1,可以構(gòu)造一些新的題目,比如如下的變式1.(解答留給讀者)

變式1f(x) = ex - x -當x≥0 時,f(x)≥+1,求a的范圍.

我們還可以通過對引理1 的推廣來得到前述高考題的進一步推廣.

引理2(1)n為正奇數(shù)時,則有ex≥

(2)設(shè)n為正偶數(shù).則有

證明設(shè)f(x)=,定義域為R.由引理1 的證明知:

(1)n為奇數(shù)時, 當x ∈(-∞,0),f′(x)＞0;x ∈(0,+∞),f′(x)＜0, 所以f(x) ≤f(x)max=f(0) = 1, 因此ex≥1+x+

(2)n為偶數(shù)時,f′(x) ≤0, 所以f(x) 在(-∞,+∞)上是減函數(shù).當x≥ 0 時,f(x) ≤f(0) = 1, 所以ex≥1+x+當x ＜0 時,f(x)＞f(0)=1,所以ex ＜1+

推廣21 +x+≤ex,n ∈N*,求a的取值范圍.

解(1)當n= 1 時,a+x≤ex,a≤ex -x,設(shè)g(x) =ex -x, 問題歸結(jié)為a≤g(x)min.由于g′(x) = ex -1.當x≥0,g′(x) ≥0;x ＜0,g′(x)＜0,所以g(x)min=g(0) = 1,因此a≤1.

(2)當n≥2 時,當x= 0 時,a ∈R.下面研究當x /= 0時的情形.

(i)當n是大于1 的奇數(shù)時,設(shè)f(x) =f′(x) =由引理2 知x ∈(-∞,0),(0,n -1) 時,f′(x)＜0;x ∈(n-1,+∞)時,f′(x)＞0.當x ∈(-∞,0)時,

以下證明:

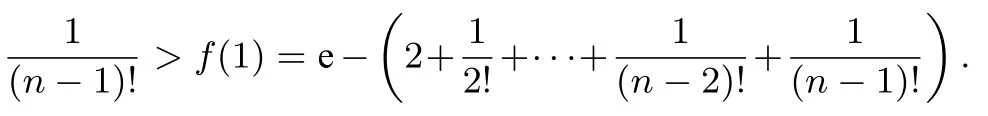
構(gòu)造函數(shù)

則a的取值范圍是(-∞,ηn-1].

(ii)當n為偶數(shù)時,當x ＜0,考慮不等式

由引理2 知

綜上所述,當n= 1 時,a的取值范圍為(-∞,1].當n為大于1 的奇數(shù)時,a的取值范圍為(-∞,ηn-1];當n為偶數(shù)時,a不存在.

根據(jù)推廣2,可以給出2020年高考全國Ⅰ卷理科第21 題如下變式:

變式2已知函數(shù)f(x)=ex+ax2-x,

(1)當a=1 時,討論f(x)的單調(diào)性.

(2)f(x)≥+1,求a的取值范圍.(答案:a≥