趙嬌,馬如云

(西北師范大學數(shù)學與統(tǒng)計學院,甘肅蘭州 730070)

1 引言

彈性梁在平衡狀態(tài)下的形變是由四階常微分方程邊值問題來描述的,近年來,關(guān)于非線性四階常微分方程兩點邊值問題解的存在性,參見文獻[1-8].

比如,文獻[1]基于壓縮映射定理研究四階兩點邊值問題

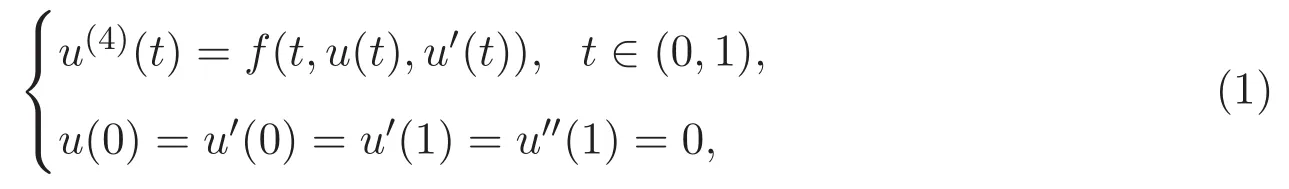
得到如下結(jié)果:

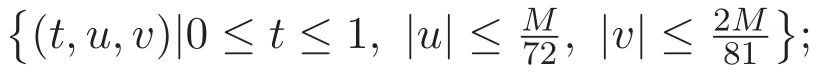
(ii)|f(t,u2,v2)?f(t,u1,v1)|≤a|u2?u1|+b|v2?v1|,(t,ui,vi)∈DM,i=1,2;

則問題(1)存在唯一解.

文獻[1]中問題(1)為一端固定支撐,一端自由滑動的梁方程,其非線性項f為連續(xù)函數(shù),工作空間是C[0,1]空間,通過運用壓縮映射定理得到定理1.1.這里注意到:文獻[1]所用工具比較簡單,由于所用工具的局限性,僅得到解的唯一性.一個自然的問題是:對于兩端固定支撐的梁方程,非線性項f為更一般的Carathéodory函數(shù)時,該用什么方法考慮解的存在性及唯一性?能否在更復雜的空間,如連續(xù)可微實值函數(shù)空間及Sobolev空間研究解的存在唯一性.基于上述考慮,本文運用Leray-Schauder延拓定理考察四階兩點邊值問題

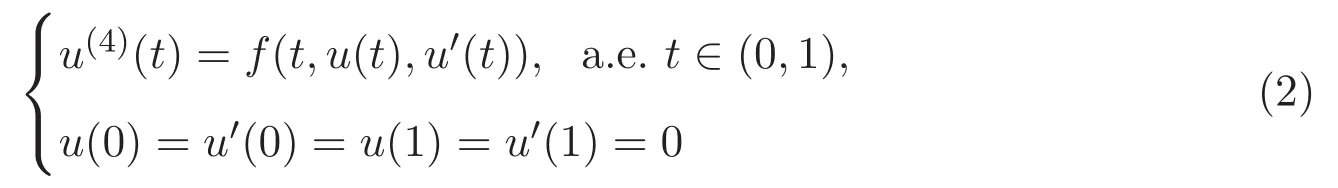
解的存在唯一性.

設(shè)Ck[0,1]為k次連續(xù)可微實值函數(shù)構(gòu)成的空間,其在范數(shù)

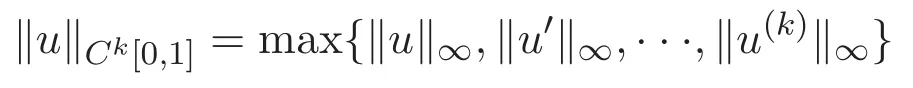
下構(gòu)成Banach空間,其中

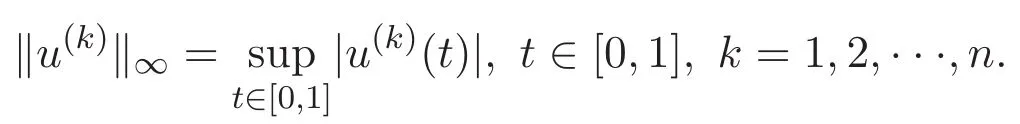
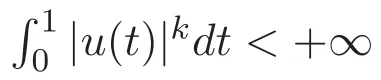
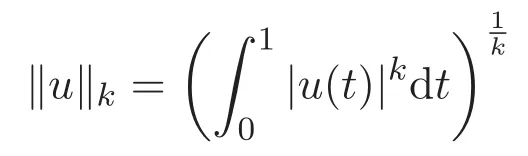
下構(gòu)成Banach空間.

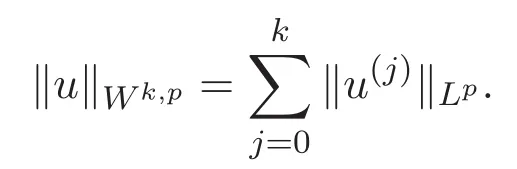
本文總假定:

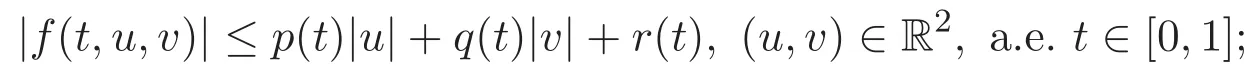
定理 1.2 若條件(H1)-(H3)成立,則問題(2)在C1[0,1]空間至少存在一個解.

定理 1.3 若條件(H1)-(H3)成立,則問題(2)在W1,2[0,1]空間至少存在一個解.

定理 1.4 若條件(H2)-(H3)成立,則問題(2)在C1[0,1]空間和W1,2[0,1]空間都有唯一解.

注 1.1 文獻[1]在非線性項f為連續(xù)函數(shù)且有界的情形下,得到了問題(1)解的唯一性.本文在非線性項 f滿足 Carathéodory條件的情形下,在 C1[0,1]空間和W1,2[0,1]空間中討論了問題(2)解的存在性和唯一性,因此推廣了文獻[1]的結(jié)果.

2 預備知識

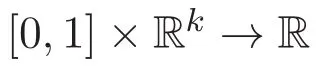
(b)對幾乎所有的 t∈[0,1],函數(shù) f(t,·)連續(xù);

引理 2.2 若h∈L1[0,1],則線性邊值問題

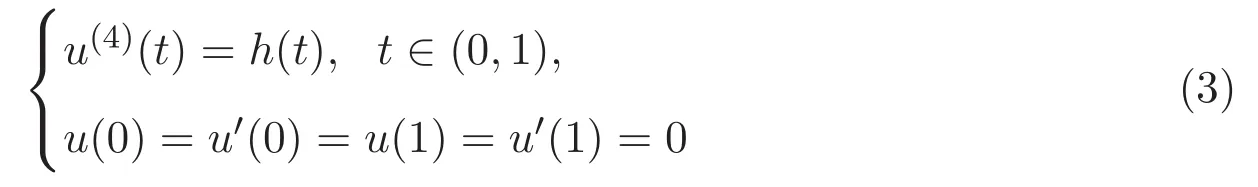
有唯一的解

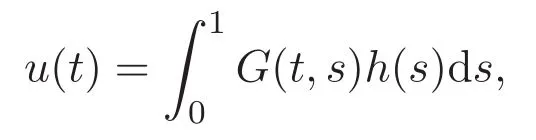
其中

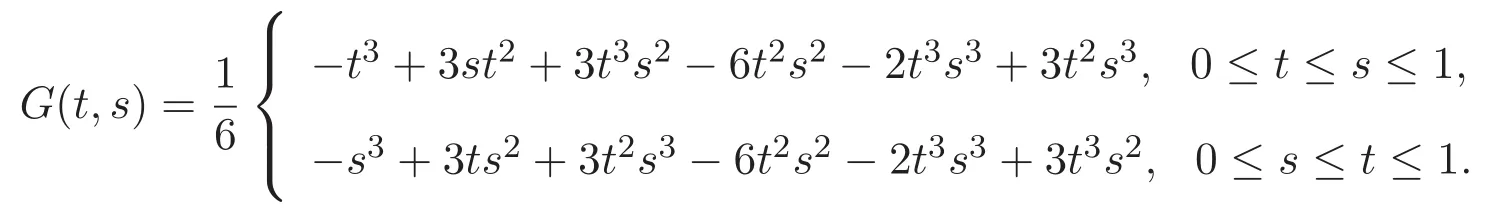
證明 因為方程u(4)(t)=0的基本解組為1,t,t2,t3,故其通解為

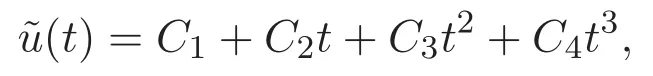
現(xiàn)通過常數(shù)變易法,可以設(shè)問題(3)的解

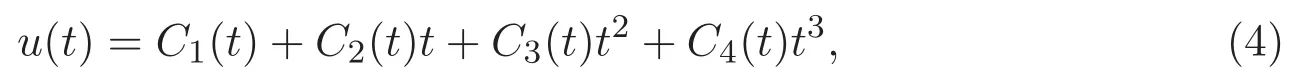
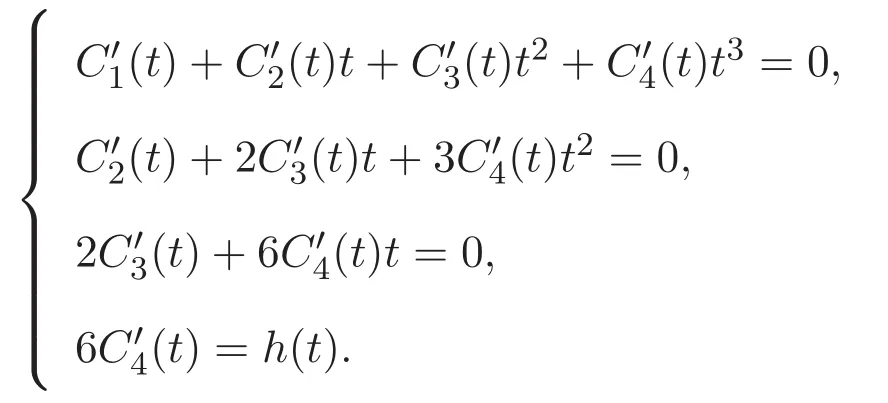
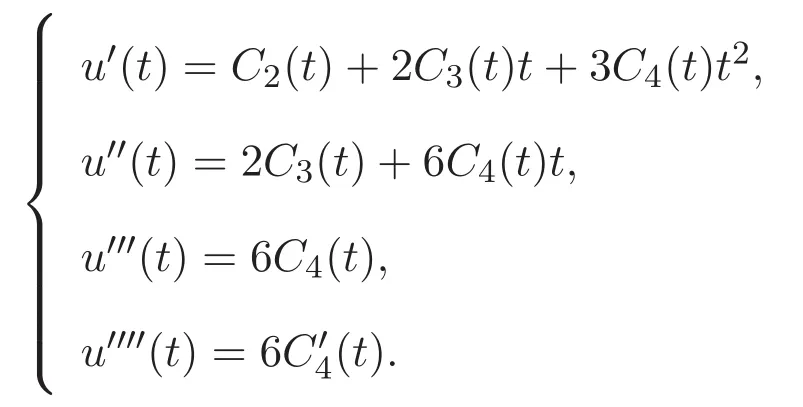
將 u(0)=u′(0)=u(1)=u′(1)=0,帶入 (4)式及上式可得

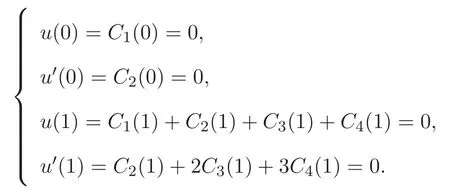
因此

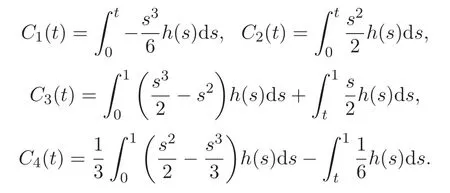
將上式帶入(4)式,進一步整理可得

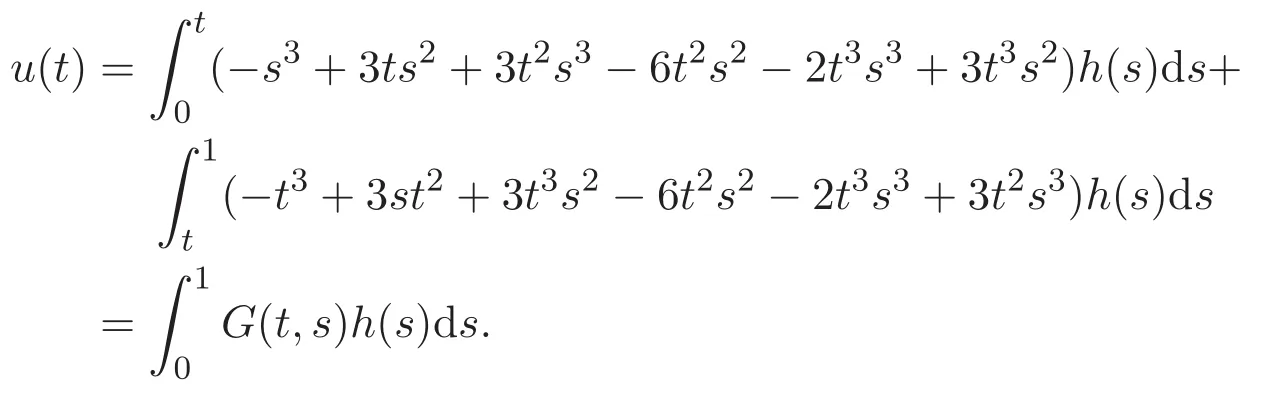
引理 2.3[10](Wirtinger不等式) 設(shè)u∈W2,2[0,1],若u(0)=u(1)=0,則

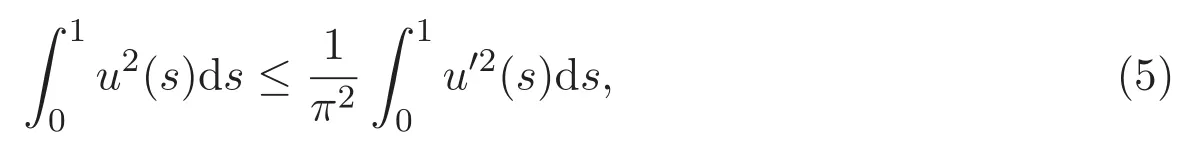
進一步,若u(0)=0或u(1)=0,則

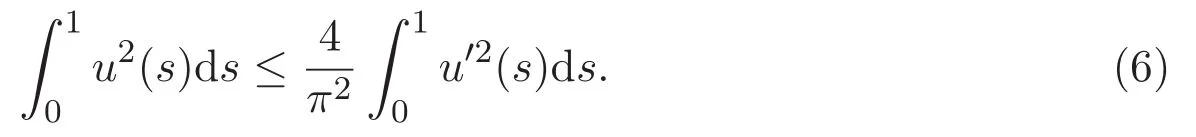
引理 2.4 若 u∈W2,2[0,1]且滿足邊界條件 u(0)=u′(0)=u(1)=u′(1)=0,則

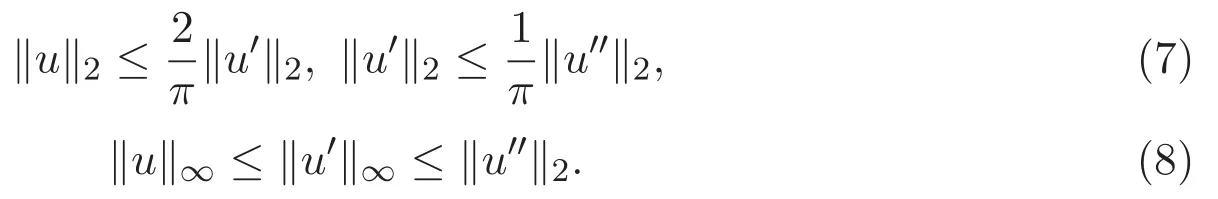
證明 第一步證明(7)式.由u(0)=0,結(jié)合(6)式可得

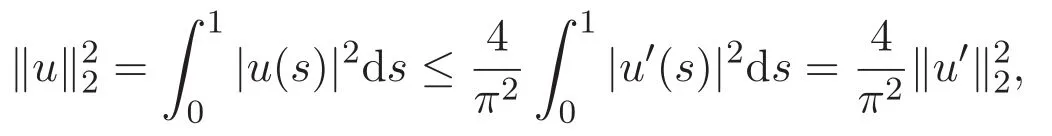
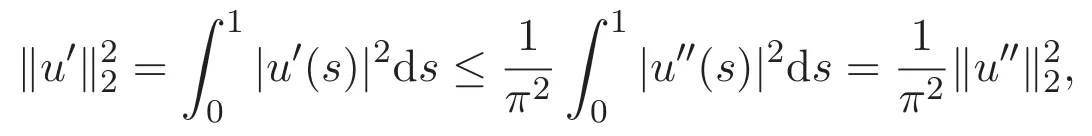
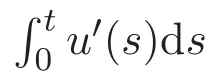
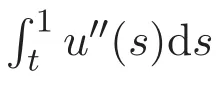
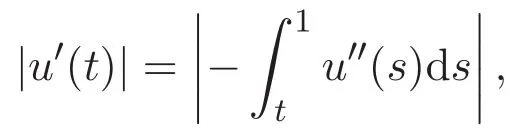
故

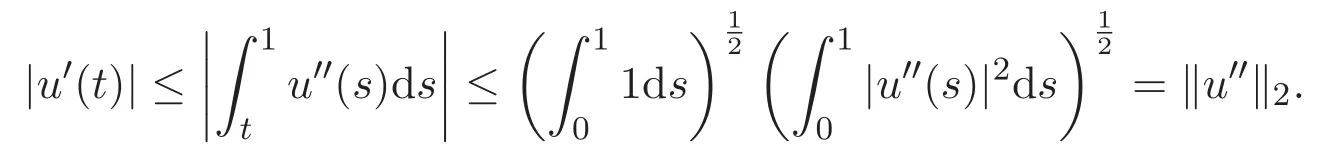
因此 ‖u‖∞≤‖u′‖∞≤‖u′‖2.

3 主要結(jié)果的證明

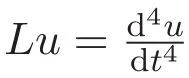
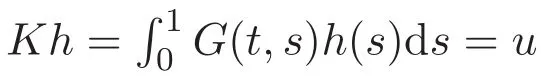
易見對任意的u∈D(L),有KLu=u及對任意的h∈L1[0,1],有LKh=h.

定義非線性映射 N:C1[0,1]→L1[0,1]為 (Nu)(t)=f(t,u(t),u′(t)),t∈[0,1].因為 f為 Carathéodory函數(shù),故根據(jù)Arzela-Ascoli定理可知,KN 將C1[0,1]中的有界集映為C3[0,1]?C1[0,1]中相對緊集.因此,KN:C1[0,1]→C1[0,1]是一個緊映射.

現(xiàn)在,u是問題 (2)的解當且僅當 u是算子方程 Lu=Nu的解.而算子方程Lu=Nu又等價于不動點問題u=KNu.下面將運用Leray-Schauder延拓定理證明u=KNu存在不動點,從而證明了問題(2)的解存在.

為證u=KNu存在不動點,只需證明同倫族問題

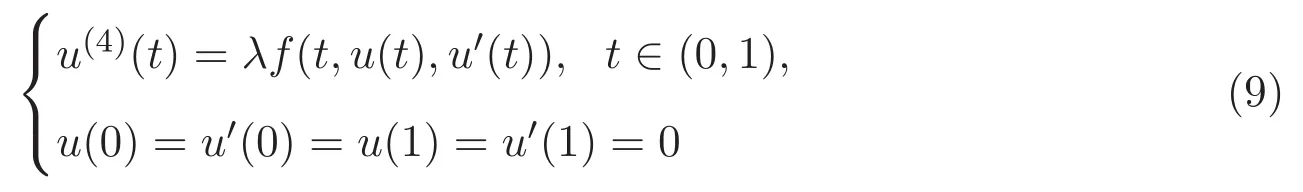
的所有可能的解有一個不依賴于λ∈[0,1]的先驗界.

設(shè)u是同倫族問題(9)的一個解,在問題(9)的方程兩端同時乘以u然后0到1上積分,進一步結(jié)合引理2.4,條件(H1)以及H′older不等式,可得

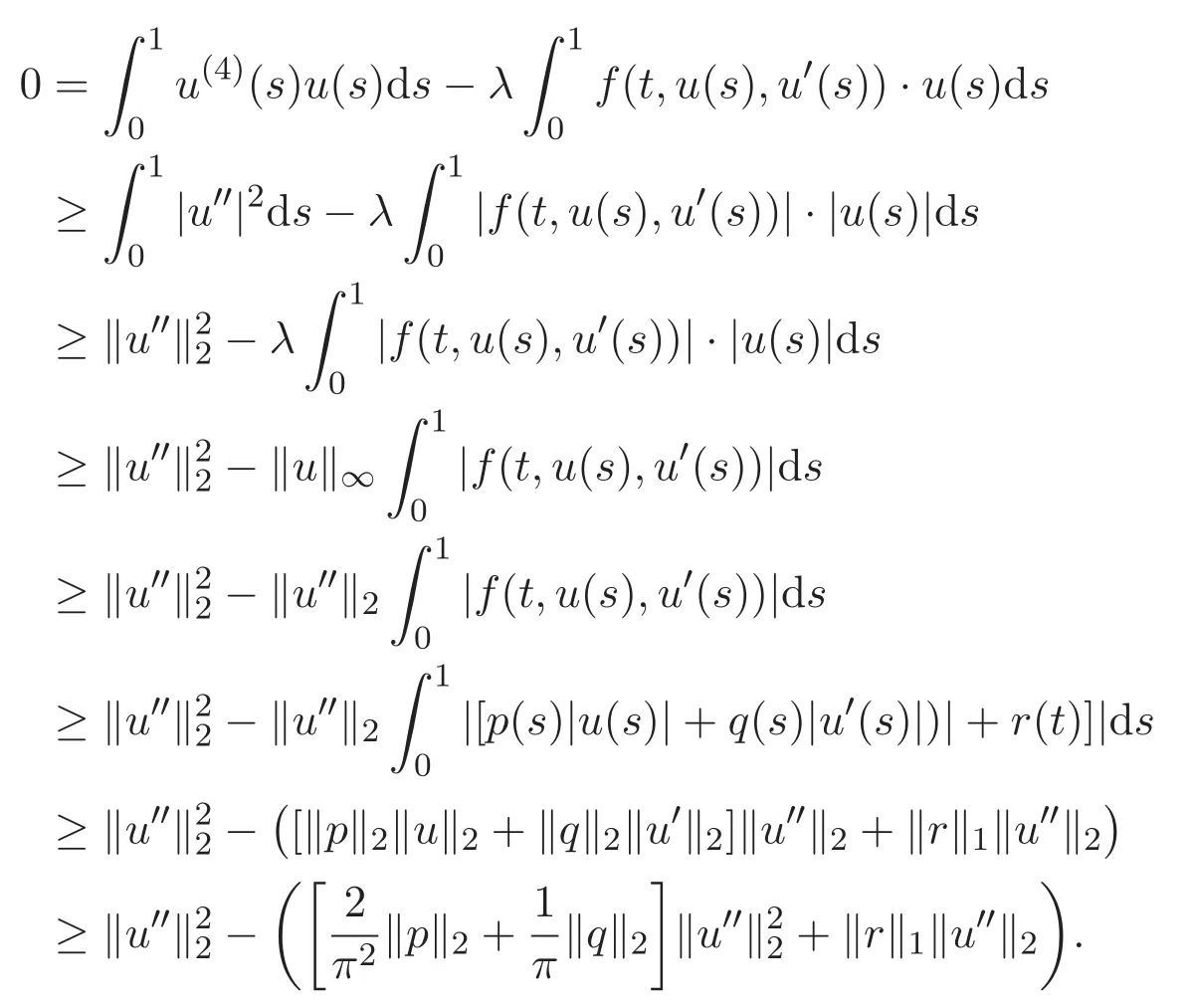
因此,

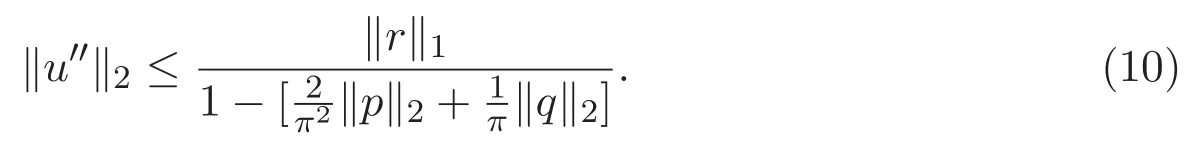
由(8)式,條件(H3)可知,存在一個不依賴λ∈[0,1]的正常數(shù)C使得 ‖u‖C1[0,1]≤C,因此,問題(2)在C1[0,1]中至少存在一個解.

定理 1.3的證明 類似于定理1.2的證明,只需證明同倫族問題(9)的所有可能的解有一個不依賴于λ∈[0,1]的先驗界.根據(jù)(7)-(8)式可得

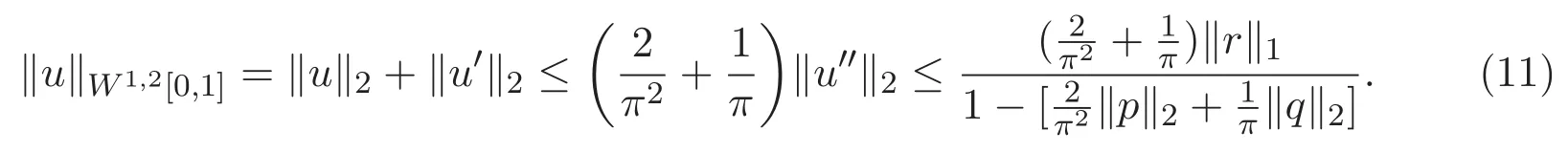
由條件(H3)可知,存在一個不依賴于λ∈[0,1]的正常數(shù)C0使得

因此,問題(2)在W1,2[0,1]中至少存在一個解.

定理 1.4的證明 令u1=u,v1=v,u2=v2=0,則根據(jù)條件(H2)可得

故條件 (H1)成立.又因為條件 (H3)成立,因此,根據(jù)定理 1.2,定理 1.3可知,問題(2)至少存在一個解.

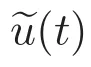
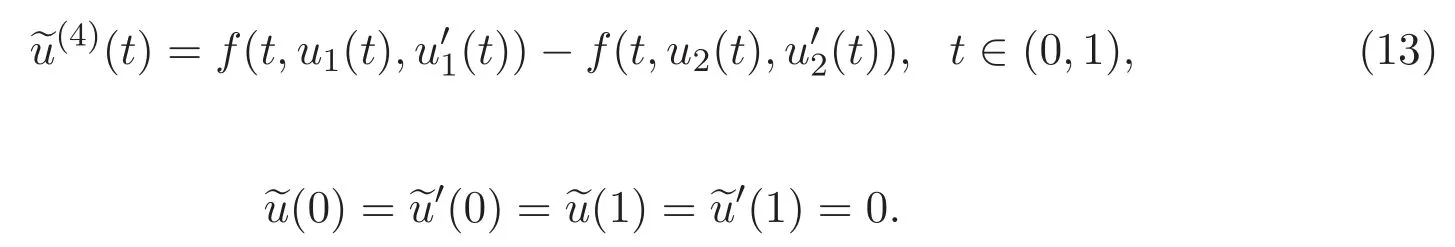
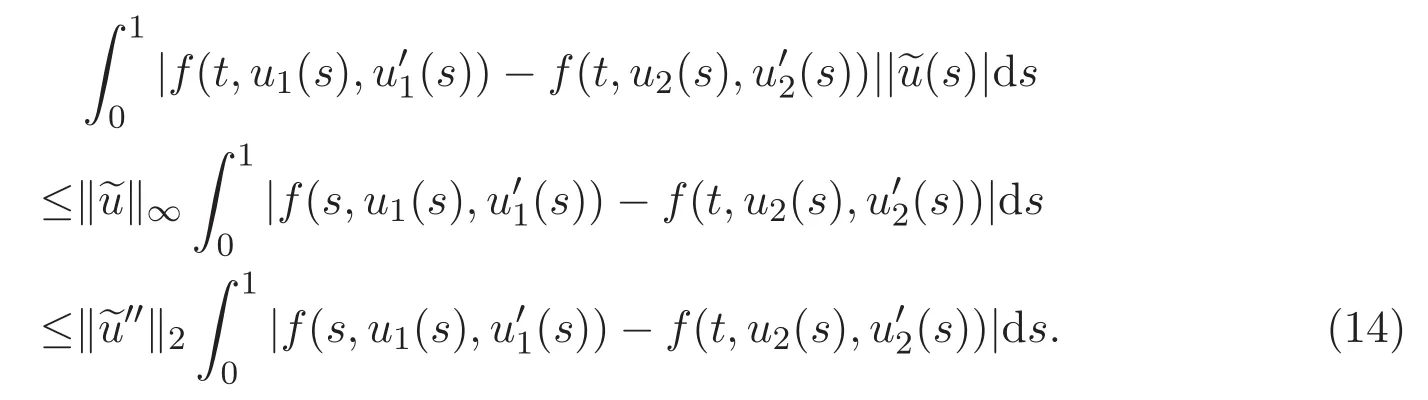
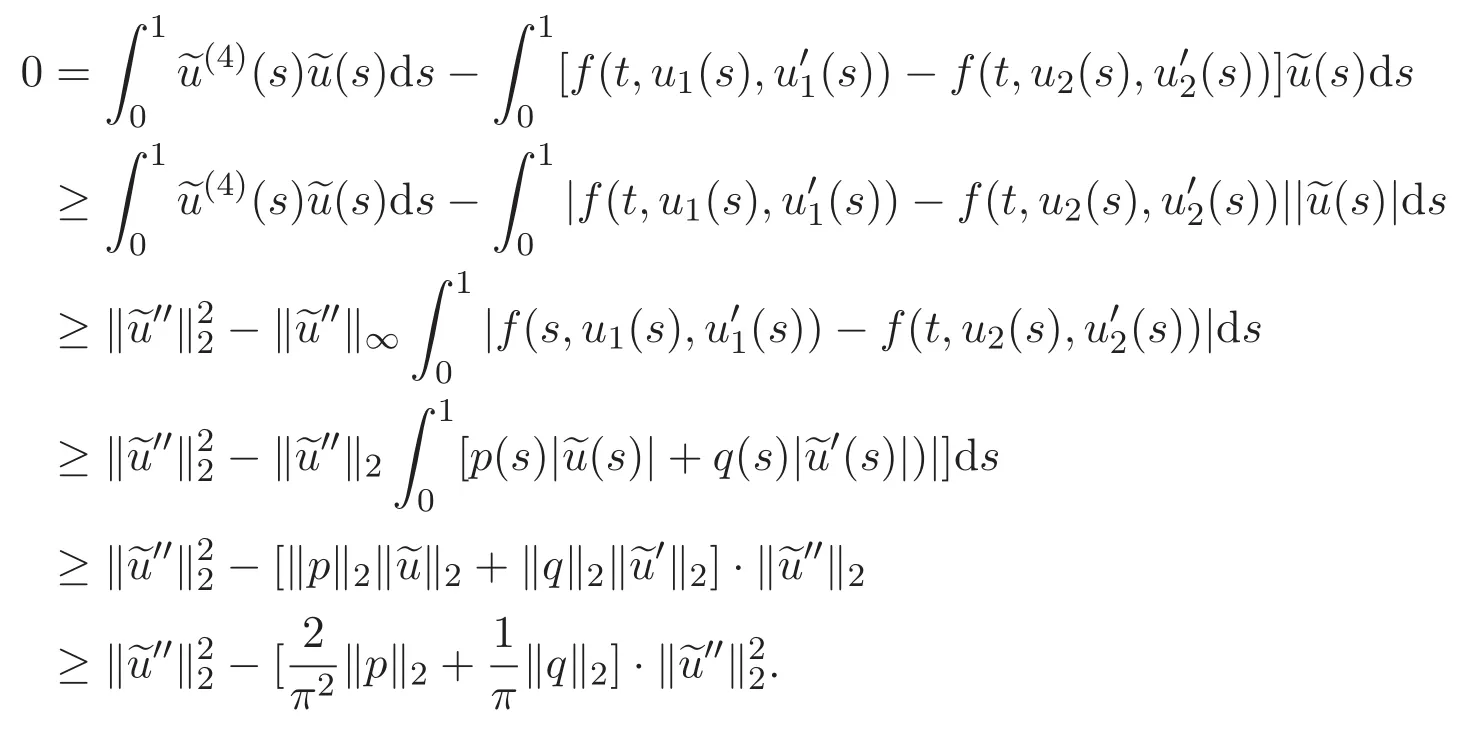
因此,

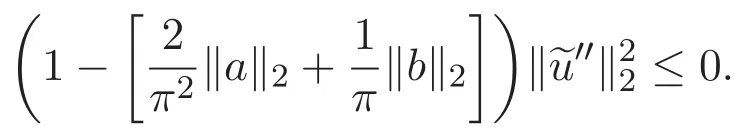
4 應(yīng)用

例4.1 對邊值問題

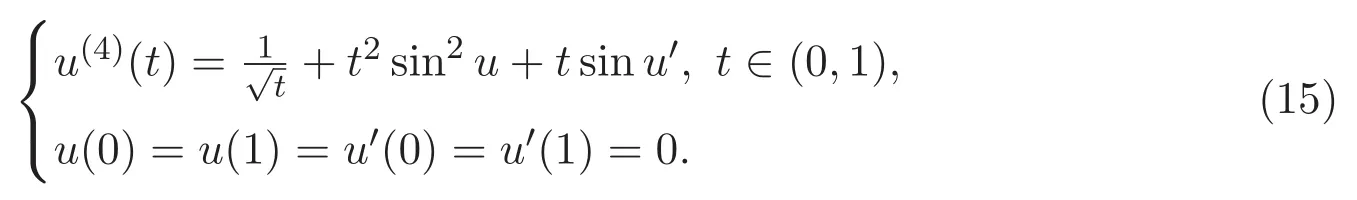
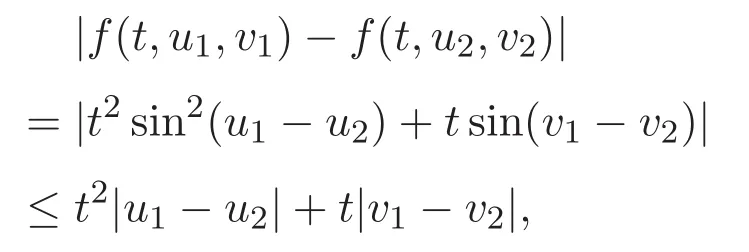
滿足條件(H2),根據(jù)定理1.4,問題(15)在C1[0,1]與W1,2(0,1)內(nèi)均存在唯一解.

根據(jù)引理2.2,所得唯一解

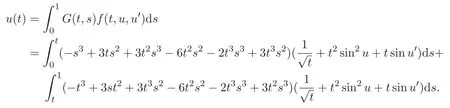
例4.2 對邊值問題

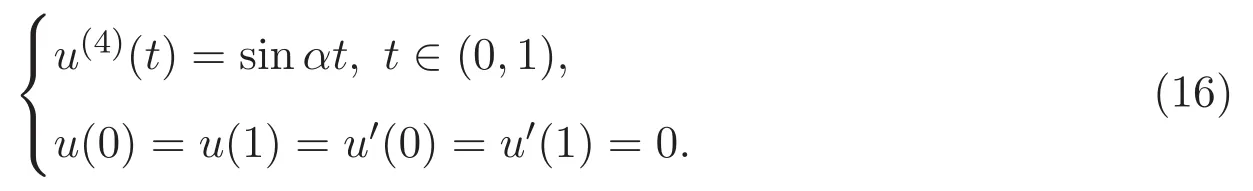
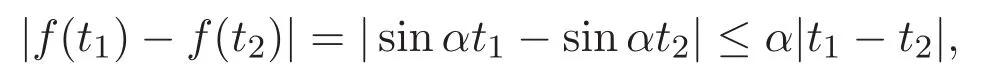
滿足條件 (H2),這里 p(t)=α,q(t)=0,顯然條件 (H3)滿足.根據(jù)定理 1.4及引理2.2可得

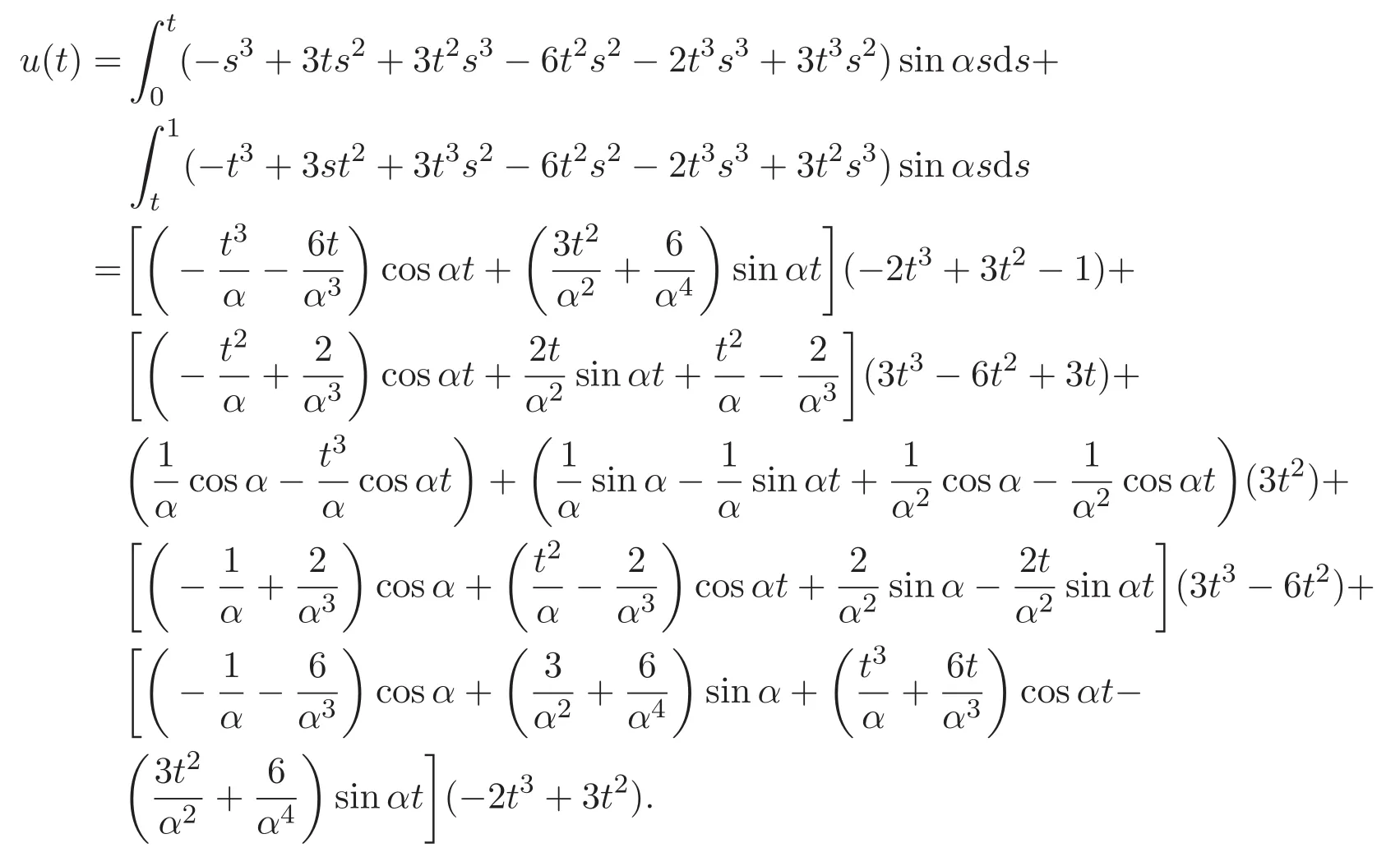
即得到問題(16)的唯一解.