田曄晨, 孫玉娟, 李路陽(yáng)

1. 西安電子科技大學(xué) 綜合業(yè)務(wù)網(wǎng)理論及關(guān)鍵技術(shù)國(guó)家重點(diǎn)實(shí)驗(yàn)室, 西安710071

2. 密碼科學(xué)技術(shù)國(guó)家重點(diǎn)實(shí)驗(yàn)室, 北京100878

3. 西安郵電大學(xué) 通信與信息工程學(xué)院, 西安710121

1 引言

由于k-旋轉(zhuǎn)對(duì)稱函數(shù)為旋轉(zhuǎn)對(duì)稱函數(shù)的擴(kuò)展, 其數(shù)量多于旋轉(zhuǎn)對(duì)稱函數(shù), 因此分析與研究k-旋轉(zhuǎn)對(duì)稱函數(shù)是一個(gè)具有重要理論意義的工作. 李泉等[18]在2012 年證明了k-旋轉(zhuǎn)對(duì)稱函數(shù)的Walsh 譜和自相關(guān)函數(shù)都滿足k-旋轉(zhuǎn)對(duì)稱特性, 并且借助容斥原理給出了k-旋轉(zhuǎn)對(duì)稱函數(shù)軌道中的長(zhǎng)圈與短圈的計(jì)數(shù)公式. 同年, 杜蛟和溫巧燕等學(xué)者[19]通過矩陣分析的方法, 得到了2p 元2-旋轉(zhuǎn)對(duì)稱函數(shù)為彈性函數(shù)的一個(gè)充要條件, 完全確定了這類彈性函數(shù)的構(gòu)造與計(jì)數(shù)方法, 其中p 為2 或奇素?cái)?shù). 2015 年, Liu 給出了一類僅由x1x2x3生成的三次2-旋轉(zhuǎn)對(duì)稱函數(shù)的漢明重量的遞歸式, 并證明了其非線性度等于其漢明重量[20].之后Reid 和Cusick[21]給出了由一個(gè)三次單項(xiàng)式生成的2-旋轉(zhuǎn)對(duì)稱函數(shù)的仿射等價(jià)類的劃分. 2020 年Su[22]基于Rothaus’s bent 函數(shù)給出了構(gòu)造n 維2-旋轉(zhuǎn)對(duì)稱bent 函數(shù)的兩種方法, 其中n ?4.

由于多輸出布爾函數(shù)在分組密碼中的廣泛應(yīng)用, 具有特殊性質(zhì)的多輸出布爾函數(shù)在密碼體制中逐步具有了重要的作用. 2009 年, 元彥斌和趙亞群[23]提出了多輸出旋轉(zhuǎn)對(duì)稱函數(shù)的概念, 研究了多輸出旋轉(zhuǎn)對(duì)稱函數(shù)的頻譜及自相關(guān)函數(shù)的特征; 給出了多輸出旋轉(zhuǎn)對(duì)稱函數(shù)滿足平衡性, 相關(guān)免疫性等性質(zhì)的充分必要條件; 并且通過研究奇數(shù)變?cè)噍敵鲂D(zhuǎn)對(duì)稱函數(shù)廣義一階Walsh 循環(huán)譜的性質(zhì), 得到了一種尋找奇數(shù)變?cè)噍敵鯬lateaued 旋轉(zhuǎn)對(duì)稱函數(shù)的方法. 之后Kavut 與高光普等學(xué)者將旋轉(zhuǎn)對(duì)稱函數(shù)與k-旋轉(zhuǎn)對(duì)稱函數(shù)用于構(gòu)造S 盒, 分別利用窮搜索法[24]和最速下降法[25]得到了旋轉(zhuǎn)對(duì)稱S 盒或k-旋轉(zhuǎn)對(duì)稱S 盒的一些性質(zhì)與結(jié)論, 并研究了置換或映射的結(jié)構(gòu). Mazumdar 等人[26,27]基于旋轉(zhuǎn)對(duì)稱函數(shù)構(gòu)造出了具有高非線性度和高DPA 攻擊抵抗力的旋轉(zhuǎn)對(duì)稱S 盒. 在平衡性與彈性方面, 杜蛟等[28]在2017 年給出了8元多輸出旋轉(zhuǎn)對(duì)稱1 階彈性函數(shù)的構(gòu)造, 并給出了該類函數(shù)的計(jì)數(shù)方法. 基于此成果, 杜蛟等[29]隨后通過求解方程組的方法, 給出了幾類平衡與彈性多輸出旋轉(zhuǎn)對(duì)稱布爾函數(shù)的存在性證明.

本文主要給出了幾類平衡(0 階彈性) 與1 階彈性多輸出k-旋轉(zhuǎn)對(duì)稱布爾函數(shù)的存在性與構(gòu)造. 后文內(nèi)容安排如下: 在第2 節(jié)中介紹了多輸出旋轉(zhuǎn)對(duì)稱與多輸出k-旋轉(zhuǎn)對(duì)稱布爾函數(shù)的相關(guān)基礎(chǔ)知識(shí), 在第3節(jié)中給出了多輸出旋轉(zhuǎn)對(duì)稱與多輸出k-旋轉(zhuǎn)對(duì)稱布爾函數(shù)軌道分布的計(jì)數(shù)公式. 第4 節(jié)主要提出了幾種平衡多輸出k-旋轉(zhuǎn)對(duì)稱布爾函數(shù)的存在性與構(gòu)造. 1 階彈性多輸出k-旋轉(zhuǎn)對(duì)稱布爾函數(shù)的部分結(jié)論在第5 節(jié)給出. 第6 節(jié)對(duì)本文工作進(jìn)行總結(jié).

2 基礎(chǔ)知識(shí)

其中1 ?i ?n.

其中k |n. 用d-軌道表示k-RSBF 中滿足|Gn,k(x)|=d 的軌道Gn,k(x).

引理1[17]令gn與gn,k分別代表n 維RSBF 與k-RSBF 不同軌道的個(gè)數(shù). 則有

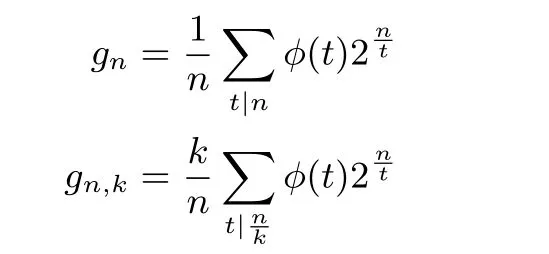
其中?(t) 是歐拉函數(shù).

由上述定義知,如果F(x)是一個(gè)(n,m)-RSBF,則對(duì)于任意的1 ?s ?m,均有fs(x)是一個(gè)RSBF.同樣地, 若F(x) 是一個(gè)(n,m) k-RSBF, 則對(duì)于任意的1 ?s ?m, 均有fs(x) 是一個(gè)k-RSBF.

定義3[29]Gn(x) 與Gn,k(x) 中的所有向量按照如下方式分別排列成兩個(gè)矩陣:

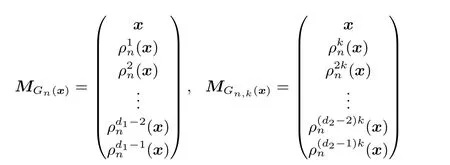
其中d1和d2分別代表Gn(x) 和Gn,k(x) 中向量的個(gè)數(shù). 換言之, | Gn(x) |= d1, | Gn,k(x) |= d2.MGn(x)與MGn,k(x)分別稱為Gn(x) 與Gn,k(x) 對(duì)應(yīng)的軌道矩陣.

3 多輸出旋轉(zhuǎn)對(duì)稱與多輸出k-旋轉(zhuǎn)對(duì)稱布爾函數(shù)的軌道分布

本節(jié)研究了(多輸出) 旋轉(zhuǎn)對(duì)稱函數(shù)和(多輸出)k-旋轉(zhuǎn)對(duì)稱函數(shù)的軌道分布情況, 并給出了計(jì)算這兩類函數(shù)中長(zhǎng)度相同軌道個(gè)數(shù)的方法.

在文獻(xiàn)[4] 中, St?nic? 和Maitra 給出了RSBF 中部分大小的軌道的計(jì)數(shù). 令hd表示n 維RSBF中大小為d 的軌道的個(gè)數(shù), 其中d | n. 我們通過使用莫比烏斯變換, 給出RSBF 不同大小的軌道的計(jì)數(shù)公式, 擴(kuò)展了文獻(xiàn)[4] 的結(jié)論.

引理3

其中d|n, μ(·) 是莫比烏斯函數(shù).

由等式(1)可計(jì)算出任意d 與k 所對(duì)應(yīng)的hd,k. 我們列出一些n 維k-RSBF 的軌道分布, 如附錄中表1 所示.

4 平衡多輸出k-旋轉(zhuǎn)對(duì)稱布爾函數(shù)的存在性與構(gòu)造

本節(jié)給出一些平衡(0 階彈性) 多輸出k-旋轉(zhuǎn)對(duì)稱布爾函數(shù)的存在性證明. 主要包含兩部分: 一是2 ?m ?p 時(shí)(pr,m) p-RSBF 的存在性; 二是k 取pr和2pr?1時(shí)平衡(2pr,m) k-RSBF 的存在性. 此外還將給出一些其他關(guān)于平衡性的結(jié)論.

在引理4[29]中, 杜蛟等人給出如下結(jié)論: 若平衡(n,m)-RSBF 存在, 則平衡(n,m ?1)-RSBF 存在.相反地, 如果不存在平衡(n,m ?1)-RSBF, 則平衡(n,m)-RSBF 也不存在. 類似地, 這一結(jié)論也適用于(n,m) k-RSBF.

引理4 若平衡(n,m) k-RSBF 存在, 則平衡(n,m ?1) k-RSBF 存在. 相反地, 如果不存在平衡(n,m ?1) k-RSBF, 則平衡(n,m) k-RSBF 也不存在, 其中k 為常數(shù).

證明: 證明方法與引理4[29]的證明方法相同. 出于篇幅的考慮, 此處不再詳細(xì)證明.

定理2 當(dāng)n=2pr, m ?2, r ?1, p 為奇素?cái)?shù)時(shí), 不存在平衡(n,m)-RSBF.

證明: 證明方法與定理2[29]的證明方法相同. 出于篇幅的考慮, 此處不再詳細(xì)證明.

已知平衡(pr,m)-RSBF 不存在, 其中p 是奇素?cái)?shù)[29]. 在(pr,m) k-RSBF 這類函數(shù)中, 令k =p, 則可得到如下結(jié)論.

定理3 令n=pr, 2 ?m ?p, k =p, 其中p 是奇素?cái)?shù), r ?2. 則平衡(n,m) k-RSBF 存在.

證明: 由引理4 知, 只需要證明平衡(pr,p) p-RSBF 的存在性(構(gòu)造出平衡(pr,p) p-RSBF). 由等式(1)計(jì)算出(pr,p) p-RSBF 的軌道分布如下:

至此, 得到平衡(pr,p) p-RSBF. 進(jìn)而由引理4 知, 當(dāng)2 ?m ?p 時(shí), 平衡(pr,m) p-RSBF 存在.

當(dāng)2 ?m ?p ?1 時(shí), 平衡(pr,m) p-RSBF 可由以下方法得到: 任意一個(gè)平衡(pr,p) p-RSBF 有2p個(gè)原像集合. 將每2p?m個(gè)原像集合進(jìn)行合并, 得到2m個(gè)大小相同的集合. 一個(gè)集合作為一個(gè)輸出的原像, 即可得到平衡(pr,m) p-RSBF, 其中2 ?m ?p ?1.

由定理2 知, 當(dāng)m ?2 時(shí), 不存在平衡(2pr,m)-RSBF. 然而, 如果選擇恰當(dāng)?shù)膋 與m, 則能夠構(gòu)造出平衡(2pr,m) k-RSBF.

定理4 設(shè)n=2pr,其中p 是奇素?cái)?shù),r ?1. (1)令k =pr,2 ?m ?n?1,則平衡(2pr,m)k-RSBF存在; (2) 令k =2pr?1, 2 ?m ?k, 則平衡(2pr,m) k-RSBF 存在.

證明: (1) 由等式(1)計(jì)算出(2pr,m) pr-RSBF 的軌道分布如下:

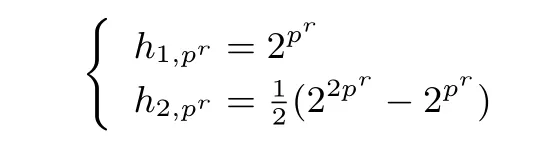
將每?jī)蓚€(gè)1-軌道合并為一個(gè)集合, 每1 個(gè)2-軌道單獨(dú)作為一個(gè)集合, 則可得到

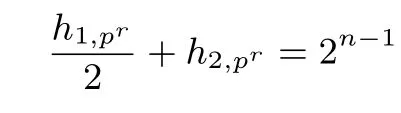
個(gè)集合,每一個(gè)集合包含2 個(gè)向量. 令一個(gè)集合作為一個(gè)輸出的原像,即可得到平衡(2pr,n?1)pr-RSBF.因此, 平衡(2pr,n ?1) pr-RSBF 存在. 進(jìn)而由引理4 知, 當(dāng)2 ?m ?n ?1, r ?1 時(shí), 平衡(2pr,m)pr-RSBF 存在.

當(dāng)2 ?m ?n ?2 時(shí), 平衡(2pr,m) pr-RSBF 可由以下方法得到: 任意一個(gè)平衡(2pr,n ?1) pr-RSBF 有2n?1個(gè)原像集合. 將每2n?m?1個(gè)原像集合進(jìn)行合并, 得到2m個(gè)大小相同的集合. 一個(gè)集合作為一個(gè)輸出的原像, 即可得到平衡(2pr,m) pr-RSBF, 其中2 ?m ?n ?2, r ?1.

(2) 由等式(1)計(jì)算出(2pr,m) 2pr?1-RSBF 的軌道分布如下:

當(dāng)2 ?m ?2pr?1?1 時(shí),平衡(2pr,m)2pr?1-RSBF 可由以下方法得到: 任意一個(gè)平衡(2pr,2pr?1)2pr?1-RSBF 有22pr?1個(gè)原像集合. 將每22pr?1?m個(gè)原像集合進(jìn)行合并, 得到2m個(gè)大小相同的集合.一個(gè)集合作為一個(gè)輸出的原像, 即可得到平衡(2pr,m) 2pr?1-RSBF, 其中2 ?m ?2pr?1?1, r ?1.

由文獻(xiàn)[28,29] 知, 當(dāng)且僅當(dāng)2 ?m ?2r?r 時(shí), 平衡(2r,m)-RSBF 存在. 事實(shí)上當(dāng)k = 2 時(shí),(2r,m) k-RSBF 也存在, 且m 的取值范圍為2 ?m ?2r?r+1.

定理5 當(dāng)n=2r, 2 ?m ?2r?r+1, k =2, r ?2 時(shí), 存在平衡(n,m) 2-RSBF.

證明: 我們利用數(shù)學(xué)歸納法進(jìn)行證明.

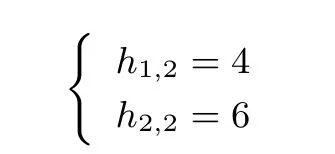
(1) 當(dāng)r =2 時(shí), (4,3) 2-RSBF 的軌道分布如下:構(gòu)造平衡(4,3) 2-RSBF 等價(jià)于將全部軌道合并為8 個(gè)集合, 且每個(gè)集合有2 個(gè)向量. 將每?jī)蓚€(gè)1-軌道合并為一個(gè)集合, 一個(gè)2-軌道作為一個(gè)集合, 則可得到8 個(gè)集合, 且每個(gè)集合包含2 個(gè)向量. 將一個(gè)集合作為一個(gè)輸出的原像, 即可構(gòu)造出平衡(4,3) 2-RSBF.

(2) 假設(shè)可構(gòu)造出平衡(2r?1,2r?1?r+2) 2-RSBF, 則可通過平衡(2r?1,2r?1?r+2) 2-RSBF 構(gòu)造出平衡(2r,2r?r+1) 2-RSBF. 構(gòu)造方法如下所示.

由等式(1)計(jì)算出(2r?1,2r?1?r+2) 2-RSBF 的軌道分布如下:

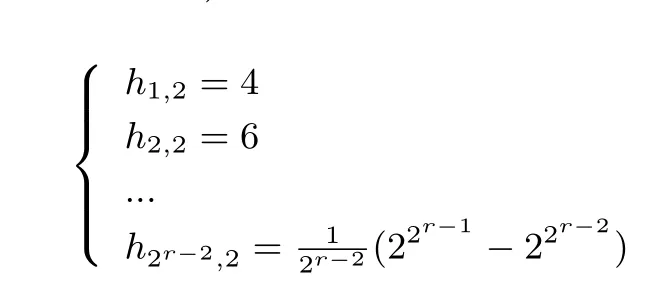
平衡(2r?1,2r?1?r+2) 2-RSBF 有22r?1?r+2個(gè)輸出, 每一個(gè)輸出對(duì)應(yīng)的原像包含2r?2個(gè)向量. 換言之, 全部軌道被合并為22r?1?r+2個(gè)集合, 每個(gè)集合含有2r?2個(gè)向量.

當(dāng)n=2r時(shí), 由等式(1)計(jì)算出(2r,2r?r+1) 2-RSBF 的軌道分布如下:

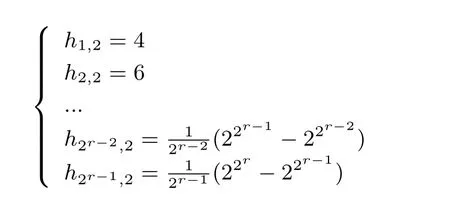
首先使用與(2r?1,2r?1?r+2) 2-RSBF 相同的軌道合并方法將(2r,2r?r+1) 2-RSBF 中全部的1-軌道, 2-軌道, 4-軌道, ···, 2r?2-軌道合并. 則可得到22r?1?r+2個(gè)集合, 每個(gè)集合包含2r?2個(gè)向量. 將上述集合兩兩合并, 則可得到22r?1?r+1個(gè)大小為2r?1的集合. 其次將每一個(gè)大小為2r?1的軌道單獨(dú)作為一個(gè)集合. 至此, (2r,2r?r+1) 2-RSBF 的所有軌道被合并為22r?r+1個(gè)大小相同的集合. 每個(gè)集合作為一個(gè)輸出的原像, 即可得到平衡(2r,2r?r+1) 2-RSBF. 進(jìn)而可知, 平衡(2r,m) 2-RSBF 存在, 其中2 ?m ?2r?r+1, r ?2.

當(dāng)2 ?m ?2r?r 時(shí), 平衡(2r,m) 2-RSBF 可由以下方法得到: 任意一個(gè)平衡(2r,2r?r +1)2-RSBF 有22r?r+1個(gè)原像集合. 將每22r?r+1?m個(gè)原像集合進(jìn)行合并, 得到2m個(gè)大小相同的集合. 一個(gè)集合作為一個(gè)輸出的原像, 即可得到平衡(2r,m) 2-RSBF, 其中2 ?m ?2r?r, r ?2.

5 1 階彈性多輸出k-旋轉(zhuǎn)對(duì)稱布爾函數(shù)的存在性與構(gòu)造

本節(jié)主要給出了1 階彈性2r維及pr維多輸出k-旋轉(zhuǎn)對(duì)稱布爾函數(shù)的存在性及構(gòu)造方法. 并給出兩個(gè)具體的例子進(jìn)行驗(yàn)證. 為了便于描述, 引出如下符號(hào)定義. 設(shè)n 維k-RSBF 中由x = (x1,x2,··· ,xn)生成的軌道為

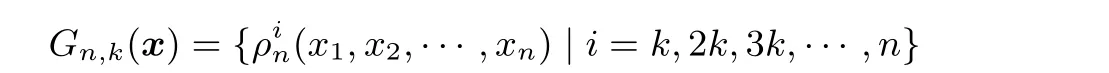
其中k |n. 則將n 維k-RSBF 中由x+1=(x1+1,x2+1,··· ,xn+1) 生成的軌道

證明: 證明方法與定理3[34]的證明方法相同. 并且由證明過程可知, d 為偶數(shù).

在定理4[29]的證明中,杜蛟等人提出: 若1 階彈性(n,m)-RSBF 存在,則1 階彈性(n,m?1)-RSBF存在. 顯然, 這一結(jié)論可擴(kuò)展至多輸出k-旋轉(zhuǎn)對(duì)稱布爾函數(shù)上: 若1 階彈性(n,m) k-RSBF 存在, 則1 階彈性(n,m ?1) k-RSBF 存在, 其中k 為常數(shù).

定理6 令n=2r, 2 ?m ?2r?r, k =2, 其中r ?3. 則1 階彈性(n,m) k-RSBF 存在.

證明: 只需證明1 階彈性(2r,2r?r) 2-RSBF 存在(構(gòu)造出1 階彈性(2r,2r?r) 2-RSBF).

1) 當(dāng)r =3 時(shí), n=8, 2 ?m ?5. 由等式1計(jì)算出(8,5) 2-RSBF 的軌道分布如下:

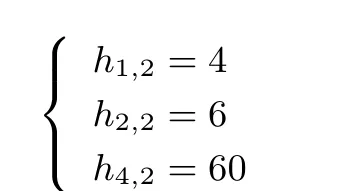
在60 個(gè)大小為4 的軌道里, 利用等式2計(jì)算可知僅有4 個(gè)特殊的軌道滿足自互反特性, 其余的軌道均按照互反規(guī)則成對(duì)出現(xiàn). 4 個(gè)特殊軌道對(duì)應(yīng)的軌道矩陣如下所示. 將56 個(gè)成對(duì)的軌道按照互反規(guī)則兩兩合并, 得到28 個(gè)集合, 即得到28 個(gè)OA(8,8,2,1). 再將四個(gè)特殊的軌道任意兩兩合并可得2 個(gè)集合, 即得到2 個(gè)OA(8,8,2,1). 至此, (8,5) 2-RSBF 的全部軌道被合并為32 個(gè)大小相同的集合, 每個(gè)集合對(duì)應(yīng)的矩陣均為一個(gè)OA(8,8,2,1). 一個(gè)集合作為一個(gè)輸出的原像, 即可構(gòu)造出1 階彈性(8,5) 2-RSBF.

2) 設(shè)n=2r時(shí), 1 階彈性(2r,2r?r) 2-RSBF 存在. 則可證明n=2r+1時(shí), 1 階彈性(2r+1,2r+1?r ?1) 2-RSBF 存在. 現(xiàn)給出由1 階彈性(2r,2r?r) 2-RSBF 構(gòu)造1 階彈性(2r+1,2r+1?r ?1) 2-RSBF的方法.

設(shè)1 階彈性(2r,2r?r) 2-RSBF 的輸出的原像對(duì)應(yīng)的正交表為

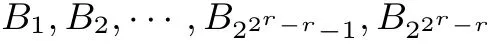
定理7 設(shè)n = pr, 2 ?m ?p ?1, k = p, 其中p 為奇素?cái)?shù), r ?2. 則1 階彈性(n,m) k-RSBF 存在.

證明: 只需證明1 階彈性(pr,p ?1) p-RSBF 存在(構(gòu)造出1 階彈性(pr,p ?1) p-RSBF).由等式(1)計(jì)算出(pr,p ?1) p-RSBF 的軌道分布如下:

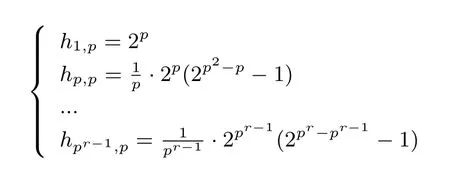
例2 設(shè)n = 32= 9, k = 3. 按照定理7 證明中的方法, 構(gòu)造出一個(gè)一階彈性(9,2) 3-RSBF:G = (g1,g2). g1與g2的真值表分別如下所示(十六進(jìn)制). 由彈性的定義知, 函數(shù)F2也是平衡的, 符合定理3 的結(jié)論.

6 總結(jié)

本文研究了幾類平衡與1 階彈性多輸出k-旋轉(zhuǎn)對(duì)稱布爾函數(shù)的存在性, 并在證明中描述了構(gòu)造的方法. 多輸出k-旋轉(zhuǎn)對(duì)稱布爾函數(shù)作為多輸出旋轉(zhuǎn)對(duì)稱布爾函數(shù)的擴(kuò)展, 除了囊括多輸出旋轉(zhuǎn)對(duì)稱布爾函數(shù)的性質(zhì)之外, 還存在部分多輸出旋轉(zhuǎn)對(duì)稱布爾函數(shù)不具有的性質(zhì). 例如n=pr時(shí), 選擇合適的k 與m, 即可構(gòu)造出平衡與1 階彈性多輸出k-旋轉(zhuǎn)對(duì)稱布爾函數(shù). 在彈性性質(zhì)方面, 目前只研究了1 階彈性性質(zhì). 是否存在滿足多階或高階彈性性質(zhì)的多輸出k-旋轉(zhuǎn)對(duì)稱布爾函數(shù)仍舊是一個(gè)有待研究的問題.