Liu Yang,Meng Fan

(School of Mathematics and Statistics,Northeast Normal University,5268 Renmin Street,Changchun 130024,Jilin,PR China)

Ravi.P Agarwal

(Department of Mathematics,Texas A&M University-Kingsville,TX78363-8202,Kingsville,TX,USA)

Abstract

Keywords p-RFDEs;existence;uniqueness;continuation;continuous dependence on initial value

1 Introduction

The pioneering work of Krasovskiˇ?[9,10]clarified the functional nature of systems with delays.The functional approach provides a foundation for the theory of differential equations with delays and the term functional differential equation(that is,FDE)is used as a synonym for systems with delays.In the framework of functional approach,different aspects of the theory of FDEs have been well developed and the systematic presentation of these results can be found in a number of excellent books[5,7,8,11,15,18,21].

In the classical theory of retarded functional differential equation(that is,RFDEs),the notation xtdefined by xt(θ)=x(t+ θ),expressing “taking into account” the history of the process x(t)considered,is the modern one introduced by Hale[6]and essentially due to Krasovskiˇ?[9].The basic theory of RFDEs has been established by many researchers.The description and classification of RFDEs are traditionally discussed by types of time-delay:finite/bounded delay,unbounded delay but finite memory,and infinite delay[12,13,21].The RFDEs with a general delay structure in a unified way were introduced from a dynamical systems viewpoint[14]based on the notation defined by Walther in[17],and hence some RFDEs with unbounded time-and state-dependent delays could be applied.

As a cornerstone of the basic theory,the unified description of RFDEs has been studied a lot.For the systems of RFDE with bounded delay and infinite delay,the unified description of state variables with delay terms can be understood easily which are presented in many monographs and papers.For the case with unbounded delay but finite memory,it can be generalized by p function,hence the corresponding system can be uniformly expressed in a general form called p-type retarded functional differential equation(p-RFDE)[12,13,20].

We now recall some basic notions for the so-called p-function and nonlinear systems of RFDE with unbounded delay but with finite memory in the sense given in[12,20].

Definition 1.1 For r＞ 0,the function p∈C(R×[?r,0],R)is said to be a p-function if it has the following properties:

(i)p(t,0)=t;

(ii)p(t,?r)is a nondecreasing function of t;

(iii)there exists a σ ≥ ?∞ such that p(t,θ)is an increasing function for θ for each t∈ (σ,∞);

(iv)p(t,0)?p(t,?r)＞ 0 for t∈ (σ,∞).

Let t0≥ 0,A ＞ 0 and x∈C([p(t0,?r),t0+A],Rn).For any t∈[t0,t0+A],with the aid of p-function,the symbol xtis defined as

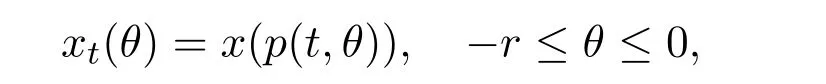
so that xt∈ C:=C([?r,0],Rn).Consider the system

where f∈C(R+×C,Rn),which is called the system of p-type RFDE(that is,p-RFDE).

The p-RFDEs have been well developed,e.g.,the basic theories were established in[12,19,20,22,23]and the existence of positive solution was explored in[1–3,16].Note that,in Definition 1.1,the conditions(i)and(iii)imply property(iv)and hence(iv)can be removed in the definition of p-function.Even though,the p-function still has great limitations so that many RFDEs in very simple form can not be classified into p-RFDE such as

Motivated by the above facts,the principal objective of the paper is to generalize the p-function and to develop a much more general description of RFDEs with unbounded delay but with finite memory.Section 2 introduces some definitions and examples of weak p-function and the generalized p-RFDE.Section 3 establishes the basic theory for generalized p-RFDEs such as the existence,uniqueness,forward continuation,continuous dependence of solutions.

2 Generalized p-RFDE

For r＞ 0,σ＞ 0,A ＞ 0,let C1:=C([t0,t0+A],Rn)with t0∈ [σ,+∞),and define

Definition 2.1 A function p∈C(R×[?r,0],R)is said to be a weak p-function if p(t,θ)satisfies the properties(i)and(iii)in Definition 1.1.

Definition 2.2 Let p(t,θ)be a weak p-function.For t0∈ [σ,+∞)and A ＞ 0,set

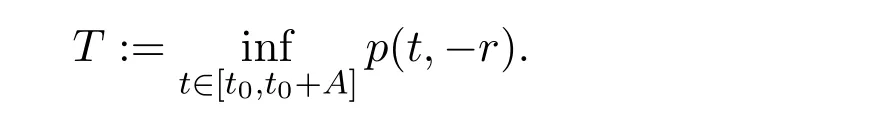
For any t∈[t0,t0+A],x∈C([T,t0+A]),Rn),define xtby

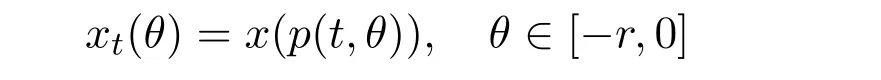
and write xt∈C.

Definition 2.3 Assume that ? ? [σ,+∞)×C is an open set and f ∈ C(?,Rn).The functional differential equation

is called generalized p-RFDE(that is,gp-RFDE)or a system with unbounded delay but with finite memory.

Definition 2.4 x(t)is said to be a solution of(2.1)if there exist t0∈ [σ,+∞)and A＞0 such that x∈C([T,t0+A),Rn),(t,xt)∈?,and x(t)satisfies(2.1)for t∈[t0,t0+A].

Definition 2.5 For any given(t0,φ)∈ ?,if there exists an A ＞ 0 such that x(t0,φ)(t)is a solution of(2.1)defined on[T,t0+A)and xt0= φ,x(t)= φ(?r),t∈[T,p(t0,?r)],then x(t)is said to be a solution of(2.1)starting from(t0,φ).

By definition,it is obvious p-RFDE is a special case of gp-RFDE.The following examples show that the gp-RFDE is a more general class of RFDE.

Example 2.1 Consider the differential-difference equation with unbounded delay

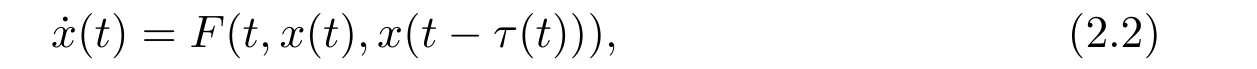
where F:R+×Rn×Rn→ Rnand τ:R+→ R+are continuous,τ(t)＞ λ with λ being a positive constant,t?τ(t)is decreasing.Take

It is not difficult to show that p(t,θ)is a weak p-function but it is not a p-function.For any t∈ [σ,∞)and ? ∈ C,set

then(2.2)is written into the form of(2.1).

Example 2.2 Consider the delay differential equation with unbounded deviating argument

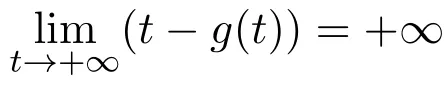
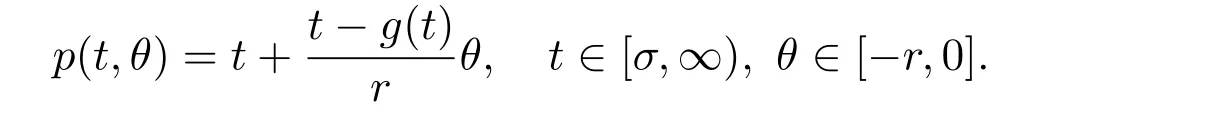
It is trivial to show that p(t,θ)is a weak p-function but it is not a p-function.(2.3)can reduce to(2.1)..Take

3 Basic Theory of gp-RFDE

Hence,T is continuous.By Schauder fixed point theorem,T has a fixed point y?∈ K.It is obvious that xy?(t)is a solution of(3.2).By Lemma 3.2,xy?(t)is a solution of(3.1)defined on[t0,t0+A].

Assume that f ∈ C(?,Rn)with ? ? R×C and(t0,φ)∈ ?.By the continuity of f,there exists an open neighborhood U ? ? of(t0,φ)such that f is bounded on U.Hence,f is bounded on.By Tietz’s extension theorem,there exists a bounded and continuous function F:R×C→Rnsuch that F|ˉU=f.By the above arguments,˙x(t)=F(t,xt),xt0=φ has a solution,say x(t0,φ)(t).If for any t∈ [t0,t0+A],one has(t,xt)∈ U,then F(t,xt)=f(t,xt).Hence,x(t0,φ)(t)is a solution of(3.1)defined on[t0,t0+A].If there exists some t1∈[t0,t0+A]such that,for any t≥ t1,(t,xt)?∈ U.Since U is an open set,we have t1＞ t0and(t,xt)∈ U for any t∈ [t0,t1).Then F(t,xt)=f(t,xt).Therefore,x(t0,φ)(t),t∈ [t0,t1)is a solution of(3.1).The proof is complete.

Theorem 3.2(Uniqueness)Assume that f ∈ C(?,Rn)with ? ? R ×C and f(t,?)is locally Lipschitz with respect to ?.Then(3.1)has a unique solution on some interval[t0,t0+α].

The proof is similar to that of Corollary 3.2 in[20].The details are omitted here.

Theorem 3.3(Continuation)Assume that f ∈ C(?,Rn)with ? ? R×C and x is a non-continuable solution of(3.1)on[t0,t0+α].Then,for any compact set W ? ?,there exists a tWsuch that(t,xt)?∈ W for tW≤ t＜ t0+α.

Theorem 3.4(Continuation)Assume that f ∈ C(?,Rn)with ? ? R × C is completely continuous and x is a non-continuable solution of(3.1)on[t0,t0+α].Then,for any bounded and closed set V ? ?,there exists a tVsuch that(t,xt)?∈ V for tV≤t＜t0+α.

The proofs of Theorems 3.3 and 3.4 are similar to those in[20]and in[13],respectively.

Theorem 3.5(Continuous Dependence)Assume that f ∈ C(?,Rn)with ? ?R×C and f(t,?)is locally Lipschitz with respect to ?,the solution x(t0,φ)(t)starting from(t0,φ)∈ ? is defined on[t0,t0+A]with A ＞ 0.Then,for any ε＞ 0,there exists a δ(ε)＞ 0 such that|xt(s,ψ)? xt(t0,φ)|＜ ε for t∈ [σ,t0+A]with σ =max{t0,s}when(s,ψ)∈ ?,|s? t0|＜ δ(ε),|ψ ? φ|＜ δ(ε).

Proof By Lemma 3.1,xt(t0,φ)is continuous in t on[t0,t0+A].Then the set{(t,xt(t0,φ)):t∈ [t0,t0+A]}is compact.Whence,there exists a sufficient small η＞0 such that

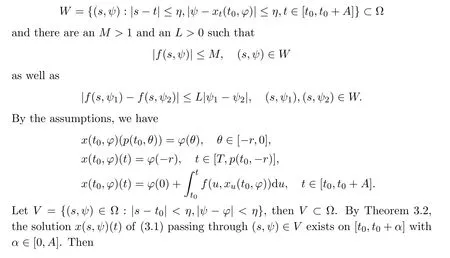
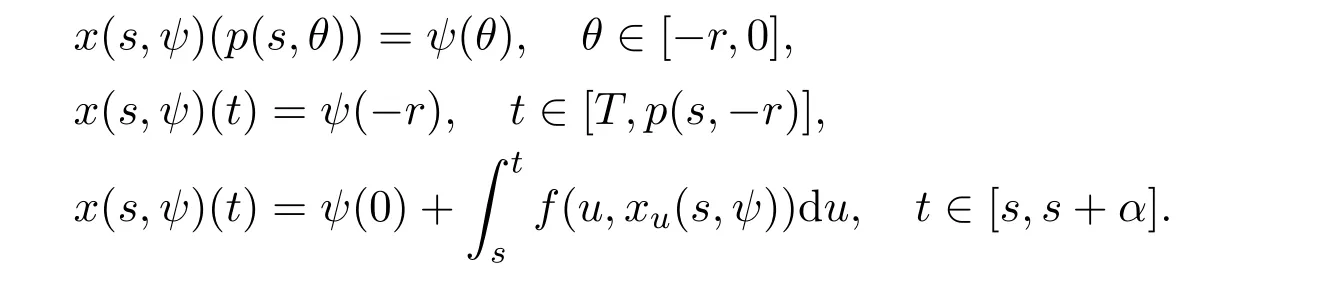
It is obvious that x(s,ψ)is continuable rightward from t provided that(t,xt(s,ψ))∈W.

Without any loss of generality,assume that 0＜s≤t0(for the case s＞t0,the proof is exactly the same).For any t∈ [t0,t0+A]such that(u,xu(s,ψ))∈ W,u∈[t0,t],one has

The above discussion holds for any t∈ [t0,t0+A]such that(t,xt(s,ψ))∈ W.

For any 0 ＜ ε＜ η,one can choose δ(ε) ＞ 0 being sufficiently small such that δ(ε) ＜ min{η,εe?LA/(2M)}and|s ? t0| ＜ δ(ε).Then,when|s ? t0| ＜ δ(ε),|ψ ? φ|＜ δ(ε),for any t∈ [t0,t0+A]such that(u,xu(s,ψ)) ∈ W,u ∈ [t0,t],one has

This means that x(s,ψ)(t)can be continuable to t0+A and(3.6)holds for any t∈[t0,t0+A].The proof is complete.