Distributed Optimization for Heterogenous Second-Order Multi-Agent Systems
Qing Zhang, Zhikun Gong, Zhengquan Yang* and Zengqiang Chen,2
(1. College of Science, Civil Aviation University of China, Tianjin 300300, China; 2. Department of Automation, Nankai University, Tianjin 300071, China)
Abstract: A continuous-time distributed optimization was researched for second-order heterogeneous multi-agent systems. The aim of this study is to keep the velocities of all agents the same and make the velocities converge to the optimal value to minimize the sum of local cost functions. First, an effective distributed controller which only uses local information was designed. Then, the stability and optimization of the systems were verified. Finally, a simulation case was used to illustrate the analytical results.
Keywords: distributed optimization; heterogeneous multi-agent system; local cost function; consensus
1 Introduction
Distributed coordination for multi-agent systems involves many aspects such as consensus and flocking. Consensus is a basic problem, in which the agent uses the distributed rule to make the system reach a common state. Gao et al.[1]studied the consensus with leader-following and without leader, respectively. Li et al.[2]demonstrated that all agents can achieve a consensus, even if the system have arbitrarily bounded communication delays.
In recent years, there are increasing studies on optimization problems. For instance, San et al.[3]presented a multi-objective optimization method to design the shape of membrane structures. Bi et al.[4]proposed a constrained optimization algorithm based on double populations to improve the distribution and convergence of the constrained optimization algorithms. However, previous researches focused on the distributed optimization problems and most of them are related to discrete-time algorithms[5-6]. Tsitsiklis et al.[7]originally presented a model for asynchronous distributed computation to achieve optimization. Li et al.[8]extended the optimization rule to the multi-agent systems, and directed topology played an important role in their research. Nedic et al.[9]formulated a projected rule for every agent in different convex sets to achieve optimization with a topology. At present, the distributed optimization problem has aroused interests of many scholars. By introducing a dynamic integrator, Wang et al.[10]presented a novel distributed rule for convex optimization. Based on the work in Ref. [10], other researchers[11-12]studied the optimization problem by strengthening conditions. Zhao et al.[13]formulated distribution optimization rule using the edge and adaptive design method on the basis of nodes. Studies in Refs. [14-15] achieved the finite-time consensus theoretically using the presented continuous forms of distributed non-smooth controllers. George and Subramanian[16]extended adaptive control with multiple models to the systems where the unknown parameters vary rapidly and frequently.
It is noteworthy that all the above results are related to the homogeneous multi-agents problems. The dynamics of the agents are always different due to the constraints in practical engineering applications, whereas the heterogeneous optimization problems have aroused little attention. Thus, given the actual situation, the study of distributed optimization with flocking of different dynamics systems is necessary both theoretically and practically. Zheng and Wang[17]created a sufficient condition of consensus for continuous-time heterogeneous systems without the measurements of velocity.
The innovations of this study are as follows. First, previous works primarily studied the consensus, while the distributed optimization problems of the heterogeneous systems have been rarely discussed. Accordingly, a distributed optimization algorithm was developed for heterogeneous system with flocking behavior to study how a group of agents can achieve optimization cooperatively. Second, this study proved the consensus and minimized the sum of the local cost functions for the heterogeneous systems.
Here is the structure of the paper. In Section 2, notations, concepts, and the preliminaries are presented, and a distributed control rule is proposed for heterogeneous multi-agent system with flocking behavior. The stability and the optimization are achieved in Section 3. The results are proved by a numerical case in Section 4, and the conclusions are drawn in Section 5.
2 Notations and Preliminaries
2.1 Algebraic Graph Theory
The notations that will be used in this paper are presented in this part.ATdenotes the transpose matrix ofA,xTrepresents the transpose vector ofx, andIn∈Rn×nrepresents the unit matrix.={1,2,…,N}.A?Bis denoted as the Kronecker product of matrixesAandB. Let ‖x‖pdenote the p-norm ofx∈Rn. The gradient of functiongisg, and the Hessian isH.
In general, an undirected graphG=(V,ε) is composed of a series of nodesV={1,2,…,N} and a set of linksε. Ifiandjcan be joined through a link (i,j), then (i,j)∈ε.Ni={j∈V:(j,i)∈ε} denotes the neighbor set of nodei. If each pair of nodes inGhas a link connected to each other, then the graphGis connected.A=[aij]∈Rn×nis a weighted adjacent matrix of the graphG, which meets the conditions: 1)aii=0; 2)aij=aji>0, if (i,j)∈ε; and 3)aij=0, if (i,j)?ε.
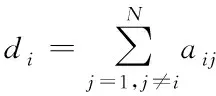
2.2 Non-smooth Analysis
Consider the differential equation with a discontinuous right-hand side[19]as
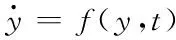
(1)
wheref:Rm×R→Rmis Lebesgue measurable and bounded.x(·) is called a Filippov solution to Eq. (1) on [t0,t1], if vector functionx(·) meets the conditions in Ref. [20].
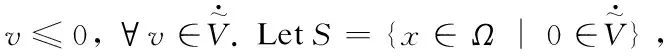
Assumption1The topology graph is undirected and connected.
Lemma2[22]Considering a continuous differentiable convex functiong(s):Rn→Ris minimized if and only if ?g(s)=0.
Lemma3[22]The second smallest eigenvalueλ2(L) of the Laplacian matrixLmeets
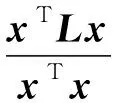
Definition1[18]g(x) isσ-strongly(σ>0) convex if and only if
(x-y)(g(x)-g(y))≥σ‖x-y‖2
forσ>0, ?x,y∈Rn, andx≠y. Ifg(x) isσ-strongly convex and twice differentiableH(x) onx, thenH(x)≥σIn.
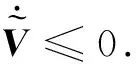
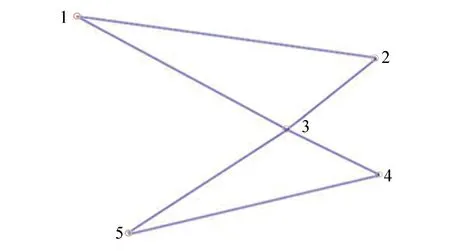
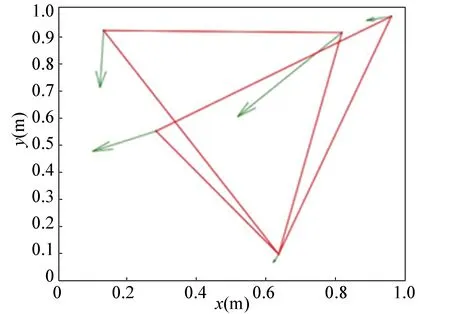
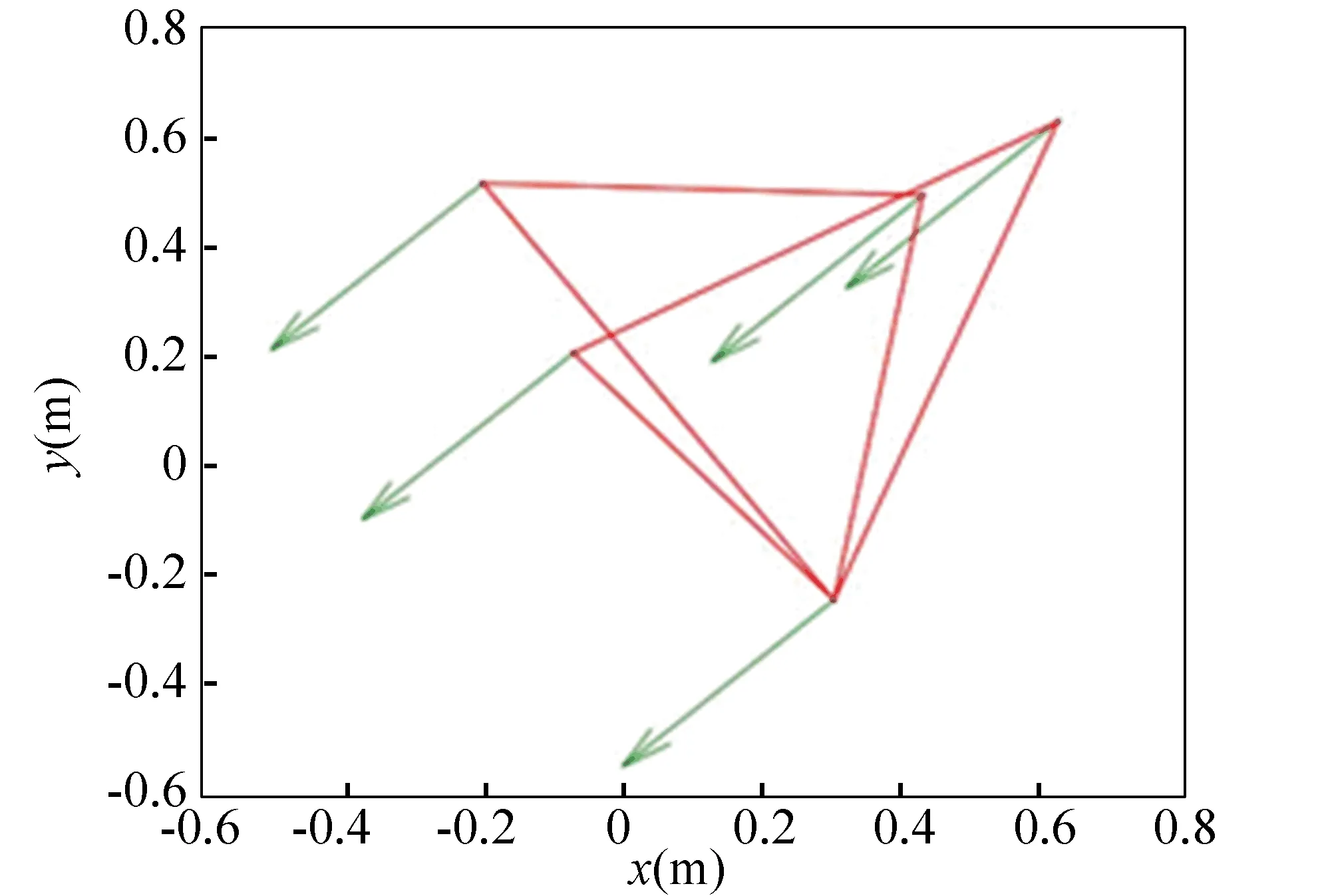
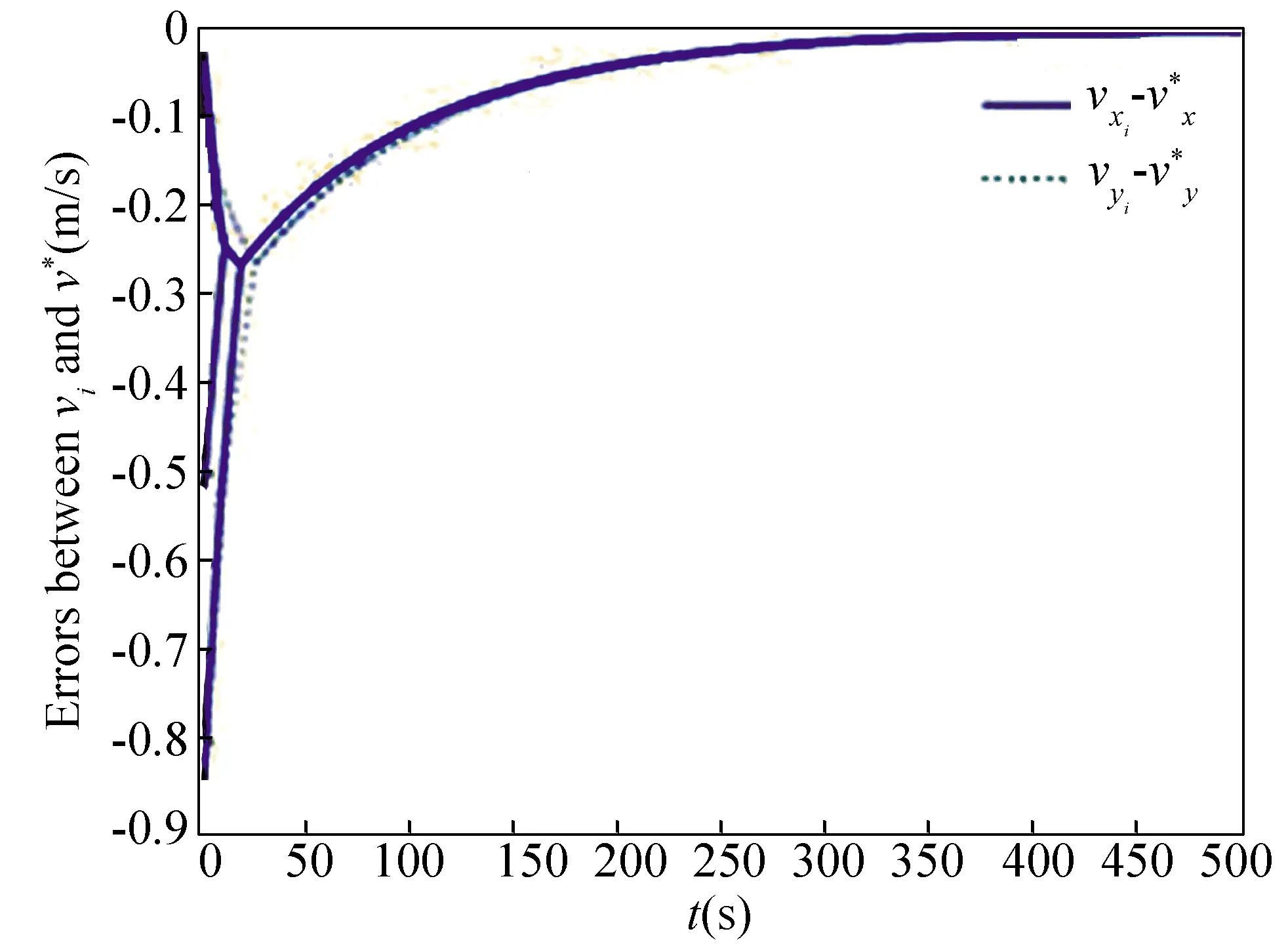
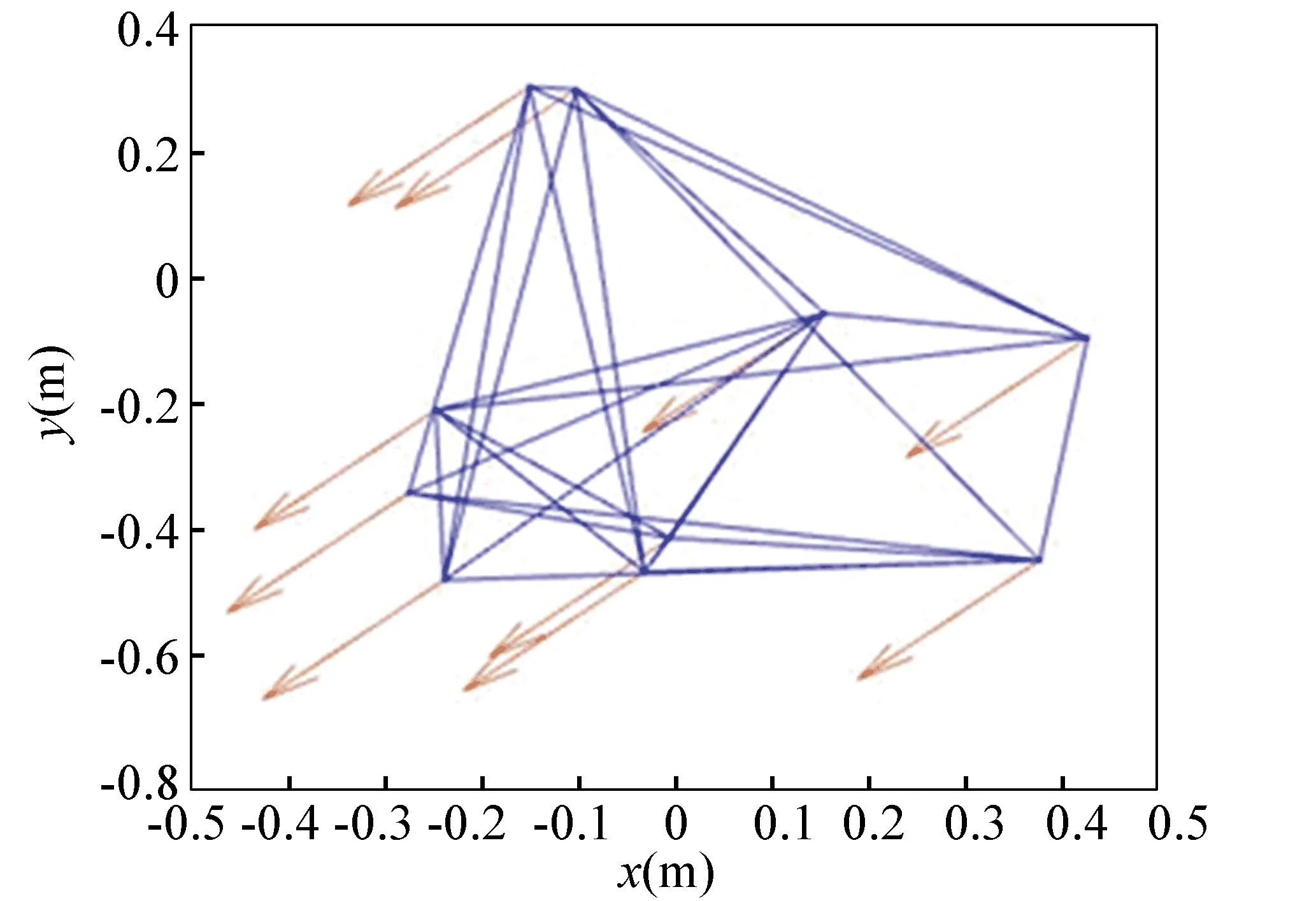
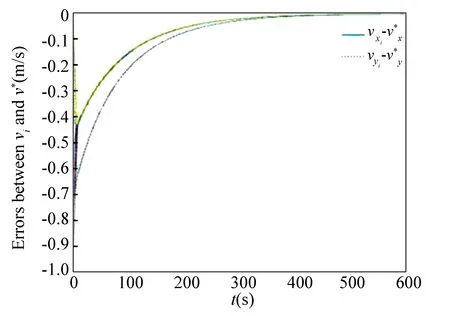
N(N>2) agent is considered withn-dimensional. ForNagents, the number of the linear agents ism, labelled from 1 tom(m (2) (3) wherexi(t)∈Rnis the position of the agenti,vi(t)∈Rnrepresents the velocity of the agenti,ui(t) is the control law of the agenti, andf(vi) is non-linear continuous function. Assumption2There exists a constant 0<ω≤1, fori=1,2,…,m, such that ‖f(vi)‖≤ω‖vi‖. The purpose of this paper is to devise a controller for Eqs. (2) and (3) that enables all agents to achieve optimization using local interactive information. (4) wheregi(s):Rn→Ris a local cost function known only to agenti, andgi(s) meets Assumptions 3 and 4. Assumption3The local cost functiongi(s):Rn→Ris convex, differentiable, and meets gi(s)=sTAis (5) The above problem is transformed into the minimization problem of function as follows: (6) A distributed rule is presented, which makes the velocities of the agents the same and minimizes the functiongi(vi). (7) where aijdescribes the communication weight between agentsiandj, and sgn(·) represents the signum function. It is noteworthy thatφirelies merely on the velocity of the agenti. The twice differentiable function of the functiongi(vi) with respect toviis HessianHi(vi). Since the control rule developed in this paper contains sign functions, the system (2)-(3) has Filippov solution[19]. Theorem1For the multi-agent system (2)-(3) with the controller (7), all agents asymptotically reach a consensus ifλ2(L)≥σ-1λ*+ω. ProofAs can be seen from Eqs. (2)-(3), the closed-loop is φi+f(vi) (8) Clearly, the right-hand side of Eq. (8) is discontinuous. Therefore, differential inclusions and non-smooth analysis can be used to illustrate the stability of system (2)-(3)[20]as wherea.e. means “almost everywhere”. Define the following function as From the properties ofκin Ref. [21], the set-valued Lie derivative ofV(t) with on time along Eq.(8) is described as By using ‖f(vi)‖≤ω‖vi‖, one gets σ-1VTBV Then, it yields Apparently, ifλ2(L)≥σ-1λ*+ω, then Asvi-vj=0 fori,j=1,2,…,N, it yields which shows that the distance is invariant. Hence, all agents become consensus and collision is avoided. Theorem2Under the Assumptions 1-4, for system (2)-(3) with the controller (7), the agents velocities are optimal and they minimize the functiongi(vi), thus the problem (4) is solved ast→. ProofDefine the following function as Then For the system (2)-(3), the nonlinear function is designed byf(vi)=ωvisinvi. This study randomly chose the initial velocity of each agent and marked it with dots. The initial status of the agent is presented in Fig.2, where the full line between the two dots represents the path of the adjacent agent, while the arrow represents the motion direction of the agent. The final stable state of the agents is shown in Fig.3. The error between the different velocity components and the optimal velocity is illustrated by Fig.4, and the error curves of different velocity components are represented by different lines. The graph shows that the velocities reached the optimal velocity. Fig.1 Communication network Fig.2 Initial configuration of agents Fig.3 Final configuration of agents Fig.4 Errors between agents and the optimal velocity The multi-agent network was formed by 10 agents. The adjacency matrix of the considered network graph is distributed by In this part, we select 10 agents which shows that the system can still achieve a stable state and velocities of the agents can reach the optimal velocity. The initial status of the agent is presented in Fig.5, where the full line between the two dots represents the path of the adjacent agent, while the arrow represents the motion direction of the agent. The final stable state of the agents is shown in Fig.6. The error between the different velocity components and the optimal velocity is illustrated by Fig.7, and the error curves of different velocity components are represented by different lines. Fig.5 Initial configuration of agents Fig.6 Final configuration of agents Fig.7 Errors between agents and the optimal velocity This study presented a distributed rule for heterogeneous systems. The optimization rule solved both consensus and optimization. First, the consensus issue was achieved for the second-order heterogeneous system, which is a more general and realistic system in accordance with Lyapunov stability theory and non-smooth analysis. Subsequently, it was shown that velocities of all agents were asymptotically optimal while minimizing the total cost function. Finally, to be recognized for the theoretical results, a simulation case was introduced. It is noteworthy that undirected topology plays an essential role.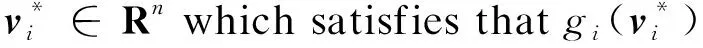
3 Main Results
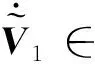
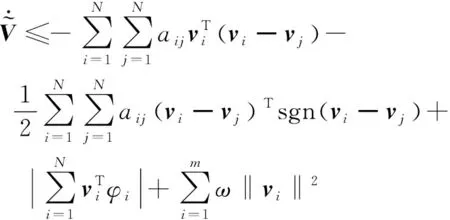
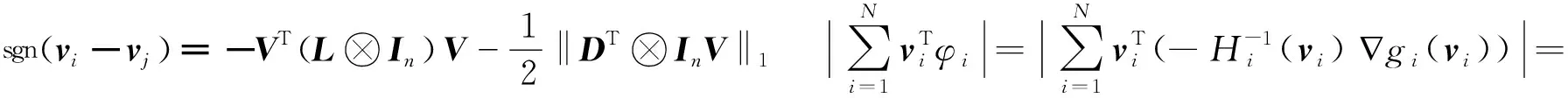
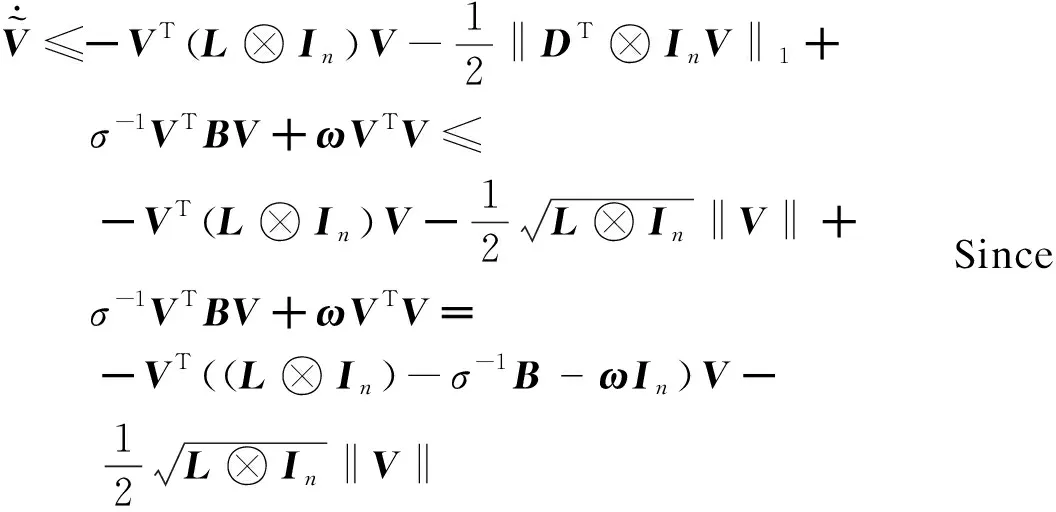
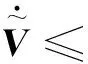
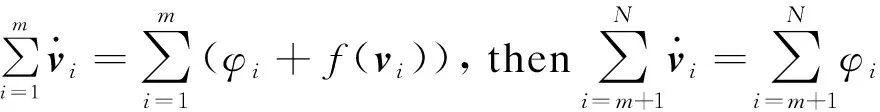
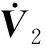
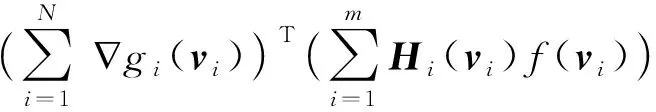
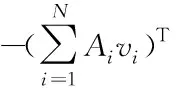
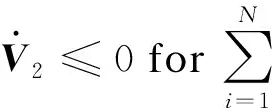

4 Numerical Simulations
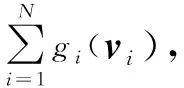
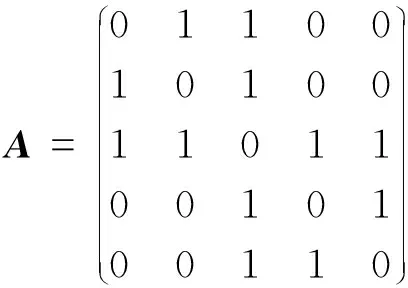


5 Conclusions
 Journal of Harbin Institute of Technology(New Series)2020年4期
Journal of Harbin Institute of Technology(New Series)2020年4期
- Journal of Harbin Institute of Technology(New Series)的其它文章
- Design of a Reflective Intensity Optical Fibre Bundle Displacement Sensor
- Fingerprint Database Updating Using Crowdsourcing in Indoor Bluetooth Positioning System
- Effects of Environments on the Noise of Atomic Force Microscopy Cantilevers
- Microbial Community Profiles Related to Volatile Fatty Acids Production in Mesophilic and Thermophilic Fermentation of Waste Activated Sludge Pretreated by Enzymolysis
- Characterisation of Bacteria-Based Concrete Crack Rejuvenation by Externally Applied Repair
- Nano-Silica Production by Rice Husk Combustion in a 0.7 MW Double-Circulating Fluidized Bed after Acid Pretreatment
