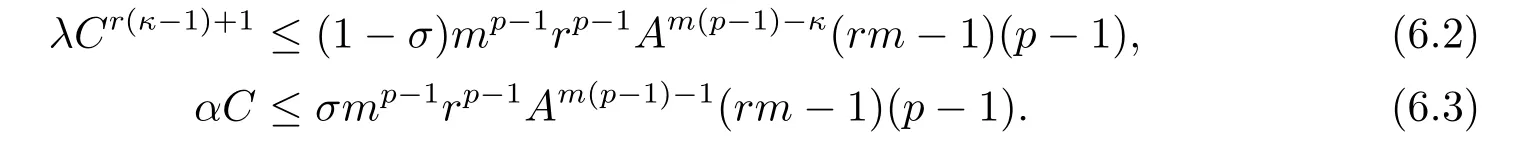A m,p-Laplacian Parabolic Equation with Nonlinear Absorption and Boundary Flux
LIU Bingchen(劉丙辰),ZHANG Changcheng(張長城),WANG Lu(王璐)
(Department of Appiled Mathematics,China University of Petroleum,Qingdao 266580,China)
Abstract: In this paper,we deal with a m,p-Laplacian equation of parabolic type in with inner absorption term (?λuκ) and nonlinear boundary flux uq.If q
Key words: m,p-Laplacian parabolic equation;Fujita-type blow-up;Global existence
1.Introduction

In this paper,we consider am,p-Laplacian equation of parabolic type The nonlinear diffusion equations (1.1) can be used to describe the nonstationary flow in a porous medium of fluids with a power dependence of the tangential stress on the velocity of displacement under polytropic conditions.
The equation (1.1) without absorption,subject to nonlinear boundary flux (1.2),has been studied by WANG,et al.in[6](i.e.,λ=0).It was proved that the blow-up phenomena are caused by the nonlinear boundary flux and the Fujita exponent is denoted byqc:=(m+1)(p?1).The results are obtained as follows.
(i) If 0≤q ≤q0:=(m+1)(p?1)/p,the solution is global;
(ii) Ifq0 (iii) Ifq >qc,both global solutions and blow-up solutions could exist. Recently,JIN,et al.[3]considered the parabolic equation ofp-Laplacian type, subject to the nonlinear boundarywhere constantsp>2,κ,q,λ>0.The critical Fujita absorption exponent has been firstly introduced in the critical case,which can be seen from the results: (i) Ifq (ii) Ifq >q?,then there exist both global solutions and blow-up solutions; (iii) Ifq=q?withλlarge,then all solutions exist globally; (iv) Letq=q?withλsmall. Ifκ ≤1,all solutions exist globally. If 1<κ<2p?1,the solutions blow up under any nontrivial nonnegative initial data. Ifκ >2p?1,there could be both global solutions and blow-up solutions for small and large initial data,respectively. The other works about the parabolic equations ofp-Laplacian type can be found in[1-2,4-5,8-10] and the papers cited there. To our knowledge,the system (1.1)-(1.3) has not been considered before.In this paper,we want to determine the critical Fujita absorption exponent for suchm,p-Laplacian equation(1.1)with absorption and boundary flux,and study how the absorption affects the global and blow-up solutions,inspired by [3,6].Moreover,we try to obtain the quantitative description about the coefficientλof the absorption term in distinguishing the existence of global solutions from blow-up solutions. The main results will be given in the next section.We also give some remarks about the influence of coefficients,the absorption and the boundary flux on the existence of global solutions and blow-up solutions of system (1.1)-(1.3).The proof of the main results can be found in Sections 3-6,respectively. For convenience,we denote a positive constant It can be found thatq?= (m+1)(p?1)/pforκ <1 andq?= (κ+m)(p?1)/pforκ ≥1,respectively.The main results are as follows. Theorem 2.1(i) Ifq (ii) Ifq >q?,then both global solutions and blow-up solutions could exist. (iii) Letq=q?.If one of the following conditions holds,then all solutions exist globally. ? κ ≤1; ?1<κ where positive constantsr:=p/[m(p?1)?κ] andMsatisfies that for any compactly supportedu0(x); ? κ>m(p?1) andλ>(κ+m)(p?1)/p; ? κ=m(p?1) andλ>mp(p?1); (iv) Letq=q?. ?If 1<κ where constantsr,C,A,α,β,σsatisfy that for smallσ ∈(0,1) and large constantC, ?Ifm(p?1)≤κ ?Ifκ>m(p?1)+p,global solutions exist for small initial data while blow-up solutions exist for large initial data,respectively. Remark 2.1The results in Theoreom 2.1 are compatible with the ones of [3] if takingm=1. Remark 2.2There is a Fujita-type blow-up result in the exponent region which is equivalent to{(p?1)(m+1) Remark 2.3The results in Theoreom 2.1 show that the existence of global and blow-up solutions was influenced not only by the exponentsp,q,mbut also by the coefficient of the absorption term in the equation (1.1).Ifq ?1<κ ? 1<κ ? m(p?1) ≤κ ? m(p?1)≤κ wheneverMis large enough.We conclude that ˉuis a global super-solution to system (1.1)-(1.3) by using the comparison principle. Next consider the caseq >q?. Proof of Theorem 2.1 (ii)Define Thenis a subsolution whenever the functionhsatisfies the inequalities and At the last section,we pay attention to the more interesting balanced caseq=q?. Proof of Theorem 2.1 (iv)Ifκ ≤1,thenq?= (m+1)(p?1)/p,and the solution always exists globally for anyλ ≥0 by the arguments for (i).Hence,it suffices to consider the caseκ>1,that is.Takeuas that for (ii) with we see that the above inequalities are ensured by Forλ<1,there exists some positive constantσ ∈(0,1)such thatλ ≤1?σ,and thus(6.2)is true.Furthermore,a direct calculation yields that(6.3)holds for appropriately large constantC.In addition,for anyu0(x)≠ 0,we haveprovided thatTis large enough,which means thatis a blow-up sub-solution according to the comparison principle. Finally,ifκ >m(p?1)+p,that is,q >(m+1)(p?1),it is known from [6] that the problem (1.1)-(1.3) withλ=0 admits global solutions for small initial data,and so does(1.1)-(1.3) withλ>0 according to the comparison principle.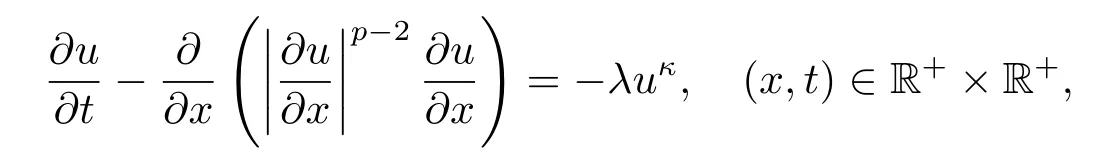
2.Main Results and Remarks
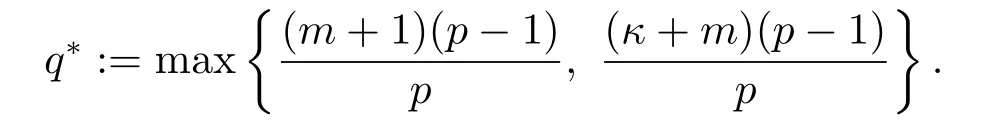
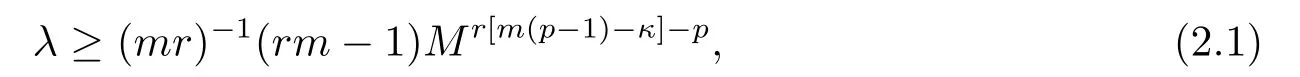
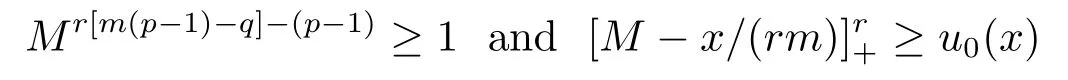
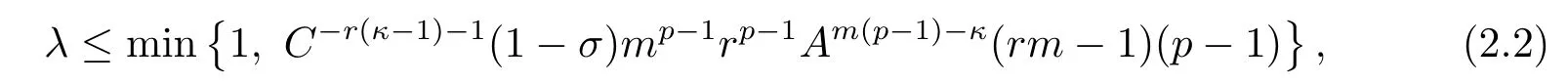

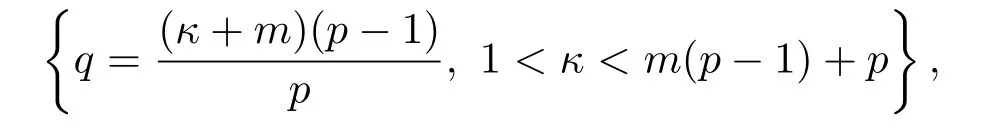
3.Proof of Theorem 2.1 (i)

4.Proof of Theorem 2.1 (ii)



5.Proof of Theorem 2.1 (iii)



6.Proof of Theorem 2.1 (iv)