Diagonal crossed product of multiplier Hopf algebras
Yan Dongdong Wang Shuanhong
(School of Mathematics, Southeast University, Nanjing 211189, China)
Abstract:Let A and B be two regular multiplier Hopf algebras. First, the notion of diagonal crossed product B#A of multiplier Hopf algebras is constructed using the bimodule algebra, which is a generalization of the diagonal crossed product in the sense of Hopf algebras. The result that the product in B#A is non-degenerate is given. Next, the definition of the comultiplication Δ# on B#A is introduced, which is composed of the multiplier ΔB(b) on B?B and the multiplier ΔA(a) on A?A, and the element Δ#(b?a) is a two-side multiplier of B#A?B#A, for any b∈B and a∈A. Then, a sufficient condition for B#A to be a regular multiplier Hopf algebra is described. In particular, Delvaux’s main theorem in the case of smash products is generalized. Finally, these integrals on a diagonal crossed product of multiplier Hopf algebras are considered.
Key words:multiplier Hopf algebra; bimodule algebra; diagonal crossed product
As is known, multiplier Hopf algebras are a generalization of Hopf algebras[1-2]. Differently from Hopf algebra, the underlying algebra is no longer assumed to be a unit, but the product of algebra is non-degenerate. Some studies of multiplier Hopf algebras and their applications can be found in Refs.[3-6]. In Ref.[7], the author considered the module algebra as a regular multiplier Hopf algebra, and the theory of smash products was generalized to multiplier Hopf algebras from Hopf algebras. The definition and properties of diagonal crossed products were introduced in Ref.[8]. In this article, we will consider the bimodule algebra as a regular multiplier Hopf algebra and generalize the theory of diagonal crossed products to the multiplier Hopf algebra case.
1 Preliminaries
Throughout this article, letkbe a fixed field of characteristic 0 (i.e., all algebraic systems are overk). In order to facilitate our computations, we always omit the summation symbolΣ.
In the following, we recall some definitions.
For an associative algebraA,Ahas a non-degenerate product with or without identity. We denote its multiplier algebra byM(A), andM(A) always contains a unit 1. In fact,M(A) can be characterized as the largest algebra with a unit, in whichAis regarded as an essential two-side ideal. Clearly,A=M(A) if and only ifAhas a unit (see the appendix in Ref.[2] for details), which is similar toM(A?A).
A comultiplication onAis a homomorphismΔA:A→M(A?A) such thatΔA(a)(1?b) and (a?1)ΔA(b) belong toA?Afor alla,b∈A, andΔAis coassociative in the sense that
(a?1?1)(ΔA?i)(ΔA(b)(1?c))=
(i?ΔA)((a?1)ΔA(b))(1?1?c)
(1)
for alla,b,c∈A, whereiis the identity map.

We say that (A,ΔA) is regular ifσΔAis again a comultiplication onAsuch that a pair (A,σΔA) is also a multiplier Hopf algebra, whereσis the flip.
Remark11) The use of the Sweedler notation for regular multiplier Hopf algebra is discussed in Ref.[1]. Takea,b∈Aas an example and considerΔA(a)(1?b). If we chooseesuch thateb=b, whereeis called the local unit (see Ref.[1], Proposition 2.2), then,ΔA(a)(1?b)=(ΔA(a)(1?e))(1?b)=a1?a2b.

Definition1[9]LetAbe a regular multiplier Hopf algebra. Then, algebraBis called anA-bimodule algebra if
1)Bis a unital leftA-module and a unital rightA-module such that (a·b)·a′=a·(b·a′);
2)a·bb′=(a1·b)(a2·b′);
3)bb′·a=(b·a1)(b′·a2) for allb,b′∈Banda,a′∈A.
2 Main Results
In this section, we will give the construction of the diagonal crossed product in the sense of multiplier Hopf algebras. More information can be found in Refs.[3-4].
Definition2LetAbe a regular multiplier Hopf algebra andBanA-bimodule algebra. Then, the diagonal crossed productB#Abuilt onB?Awith multiplication is given as
(b?a)(b′?a′)=b(a1·b′·S-1(a3))?a2a′
(2)
for allb,b′∈Banda,a′∈A. Note that on the right side, each decomposition is well-covered.
We will further investigate the algebraB#A.
Lemma1LetAbe a cocommutative multiplier Hopf algebra andBis a regular multiplier Hopf algebra such thatBis anA-bimodule algebra. Then, the product inB#Ais non-degenerate.
ProofSuppose thatbi#ai∈B#Aand that (bi#ai)(b#a)=0 for allb∈Banda∈A. Then, according to the definition of the product inB#Aand the non-degeneracy of the product inA, we have
bi(ai1·b·S-1(ai3))#ai2=0
ApplyingΔandS, multiplying withafrom the right and replacingbbya″b, we can obtain
bi(ai1a″·b·S-1(ai4))?S(ai2)a?ai3=0
for allb∈Banda,a′,a″∈A. Replacinga″ byS(ai2)a, we have
bi(ai1S(ai2)a·b·S-1(ai4))?ai3=0
That is
bi(a·b·S-1(ai2))?ai1=0
As thatAis cocommutative, we can obtain
bi(a·b·S-1(ai1))?ai2=0
ApplyingΔagain, multiplying witha′ from the left and replacingbbyba″, we obtain

Hence,bi(a·b·a′)?ai=0. Note thatBhas a non-degenerate product and it is a unital leftA-module and a unital rightA-module, and we obtainbi?ai=0.
On the other hand, suppose that (b#a)(bi#ai)=0 for allb∈Banda∈A. Similar to the proof of Lemma 5.6 in Ref.[1], we can obtainbi?ai=0.
Moreover, we will construct a comultiplication for the diagonal crossed product such that it admits a structure of multiplier Hopf algebra. First, we give two maps as follows.
LetAandBbe regular multiplier Hopf algebras such thatBis anA-bimodule algebra. The multiplication of diagonal crossed productB#Ais defined by two twist mapsR:A?B→B?Aviaa?ba1·b?a2andR′:B?A→B?Aviab?ab·S-1(a2)?a1. It can easily be checked thatRandR′ are two bijections.R-1:B?A→A?Bviab?aa2?S-1(a1)·bandR′-1:B?A→B?Aviab?ab·a2?a1.
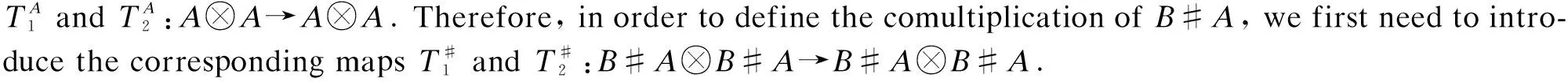

b1#a1?b2(a2·b′·S-1(a4))#a3a′

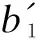
Definition3For allb,b′,b″∈Banda,a′,a″∈A, we define
Δ#(b#a)(b″#a″?b′#a′)=
b1(a1·b″·S-1(a3))#a2a″?b2(a4·b′·S-1(a6))#a5a′
and
(b″#a″?b′#a′)Δ#(b#a)=


Lemma2For anyb∈Banda∈A,Δ#(b#a) is a two-sided multiplier ofB#A?B#A.




(b″#a″?1#1)(b1#a1?b2(a2·b′·S-1(a4))#a3a′)=
Lemma3The comultiplicationΔ#is coassociative onB#A.

For allb,b′,b″∈Banda,a′,a″∈A, we have

b12#a12?b2(a2·b″·S-1(a4))#a3a″)
and
b22(a22·b″·S-1(a4))#a3a″)

Before we proceed to give the main result, we need the following definition and lemma.
Definition4LetAandBbe regular multiplier Hopf algebras andBis anA-bimodule algebra. Then,Bis anA-bimodule bialgebra if
(3)
ε#(a·b·a′)=εA(a)εB(b)εA(a′)
(4)
for allb,b′∈Banda,a′∈A. Observe that on the right side, all decompositions are well-covered.
Lemma4AandBare the same as those in Definition 4. We denote the antipode ofB(A, resp.) bySB(SA, resp.). Then,
a·SB(b)·a′=SB(a·b·a′)
The proof is straightforward.
Now, we can formulate the main result as follows.
Theorem1LetAbe a cocommutative regular multiplier Hopf algebra andBis a regular multiplier Hopf algebra such thatBis anA-bimodule bialgebra. Then,Δ#is a comultiplication onB#Asuch that (B#A,Δ#) is a regular multiplier Hopf algebra.
ProofAccording to Proposition 2.9 in Ref.[10], our proof is given as follows.
First, we can easily check that the diagonal crossed productB#Ais an associative algebra, and we prove that it has a non-degenerate product by Lemma 1.
The comultiplicationΔ#as a multiplier ofB#A?B#Ais coassociative by Lemma 3. We now show that Δ#:B#A→M(B#A?B#A) is a homomorphism. For allb,b′,b″∈Banda,a′,a″∈A, we have
Δ#(b#a)(Δ#(b′#a′)(1#1?b″#a″))=



Δ#(b(a1·b′·S-1(a3))#a2a′)(1#1?b″#a″)=
Δ#((b#a)(b′#a′))(1#1?b″#a″)
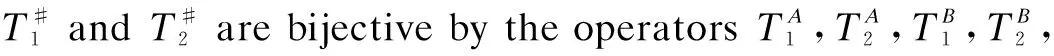
There is a counitε#defined as
ε#(b#a)=εB(b)εA(a)
for allb∈Banda∈A. It can easily be checked that these two equations (ε#?i)(Δ#(b#a)(1#1?b′#a′))=(b#a)(b′#a′) and (i?ε#)((b′#a′?1#1) Δ#(b#a))=(b′#a′)(b#a) are valid. From Eq.(4), it easily follows thatε#is a homomorphism.
There is an invertible antipodeS#defined as
S#(b#a)=R′oRo(SA?SB)oσ(b#a)=
SA(a3)·SB(b)·a1#SA(a2)∈B#A
For anyb,b′∈Banda,a′∈A, we obtain
m#(S#?iB#iA)(Δ#(b#a)(1#1?b′#a′))=
m#(S#?iB#iA)(b1#a1?b2(a2·b′·S-1(a4))#a3a′))=
m#(S(a3)·S(b1)·a1#S(a2)?b2(a4·b′·S-1(a6))#a5a′)=(S(a5)·S(b1)·a1)(S(a4)·
(b2(a6·b′·S-1(a8)))·a2)#S(a3)a7a′=
S(a3)·(S(b1)b2(a4·b′·S-1(a6)))·a1#S(a2)a5a′=
εB(b)b′·S-1(a4)·a1#S(a2)a3a′=εB(b)εA(a)b′#a′=
εB#A(b#a)(b′#a′)
Similarly, we can obtain
m#(iB#iA?S#)((b′#a′?1#1)Δ#(b#a))=
εB#A(b′#a′)(b#a)
Using Lemma 4, we can easily prove thatS#is an anti-homomorphism.
Finally, we can easily observe that the multipliersΔ#(b#a)(b′#a′?1#1) and (1#1?b′#a′)Δ#(b#a) are inB#A?B#A.
The proof is complete.
In Theorem 1, if the right action is trivial, we have the following corollary which is the main result of Ref.[7].
Corollary1LetAbe a cocommutative multiplier Hopf algebra andBis a regular multiplier Hopf algebra such thatBis anA-bimodule bialgebra. Then,Δ#is a comultiplication onB#Asuch that the smash product (B#A,Δ#) is a regular multiplier Hopf algebra.
In Ref.[10], for multiplier Hopf algebras, there is a natural notion of left and right invariance for linear functionals (called integrals in the theory of Hopf algebra). We now suppose thatAandBare multiplier Hopf algebras which are the same as those in Theorem 1. Furthermore, we suppose thatAandBhave invariant functions. In the following proposition, we will give these integrals on (B#A,Δ#).
Proposition1AandBare the same as those in Theorem 1. LetφB(φA, resp.) be a left integral ofB(A, resp.). Then,φB?φAis the left integral ofB#A. The same statement yields for the right integral.
 Journal of Southeast University(English Edition)2020年2期
Journal of Southeast University(English Edition)2020年2期
- Journal of Southeast University(English Edition)的其它文章
- Online SOC estimation based on modified covariance extended Kalman filter for lithium batteries of electric vehicles
- Consumers’ privacy data sharing between the seller and the e-commerce platform
- Influence evaluation of titania nanotube surface morphology on the performance of bioelectrochemical systems
- A customized extended warranty policy with heterogeneous usage rate and purchasing date
- Arterial traffic signal coordination modelconsidering buses and social vehicles
- Prediction method of restoring force based on online AdaBoost regression tree algorithm in hybrid test
