Multiplicity of Solutions for a Singular Elliptic System with Concave-convex Nonlinearities and Sign-changing Weight Functions
Wu Zijian Chen Haibo
(School of Mathematics and Statistics, Central South University, Changsha, Hunan 410083, China)
Abstract In this paper, we consider the multiplicity of solutions for a singular elliptic system with both concave-convex nonlinearities and sign-changing weight functions in bounded domains. Under some appropriate assumptions, we obtain that the system has at least two nontrivial solutions by using the Nehari manifold and fibering map.
Key words Singular elliptic system Concave-convex nonlinearity Sign-changing weight function Nehari manifold
1 Introduction and main result
Let Ω(0∈Ω) be a smooth bounded domain in RNwithN≥3. We are concerned with the following elliptic system:
(1.1)



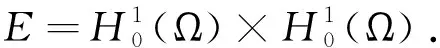
we easily derive that

The critical points of the functionalIλ,μare in fact weak solutions of (1.1). We say that (u,v)∈Eis a weak solution of (1.1) if the identity
holds for all (ω1,ω2)∈E.
Setα=β=p/2,u=v,λ=μandf=g. Then problem (1.1) reduces to the scalar singular elliptic equations with concave-convex nonlinearities:
(1.2)

Moreover, for the elliptic systems with concave-convex nonlinearities, Wu [3] considered the following problems:
(1.3)
where the weight functionsf,g,hsatisfy the following conditions:


With the help of the Nehari manifold, the author proved this system has at least two nontrivial solutions when the pair of the parameters(λ,μ) belongs to a certain subset ofR2. Furthermore, Hsu [4] considered the following problems:
(1.4)
whereλ,μ>0 andα+β=2*. The author obtained the existence and multiplicity results of positive solutions by variational methods. For more similar problems, we refer to Ahammou [5], Alves et al. [6], Bozhkov and Mitidieri [7], Zhen and Zhang [8], and Squassina [9], and so forth.
However, to our knowledge, there are only a few results in the study of problem (1.1) with concave-convex nonlinearities and sign-changing weight functions. In this paper, we extend the method of [21,22,23] to study the multiplicity of nontrivial solutions of problem (1.1). Let
and

Theorem 1.1Assume that (A),(B) hold. If (λ,μ)∈Θ, then problem (1.1) has at least two solutions (u+,v+) and (u-,v-).

2 Preliminaries
In this section, we introduce some preliminaries. As the energy functionalIλ,μis not bounded below onE, it is helpful to consider the functional on the Nehari manifold
Thus, (u,v)∈Nλ,μif and only if
(2.1)
ObviouslyNλ,μis a much smaller set thanEand, as we shall show,Iλ,μis much better behaved onNλ,μ. Note thatNλ,μcontains all nonzero solutions of (1.1). Moreover, we have the following lemma.
Lemma 2.1The energy functionalIλ,μis coercive and bounded below onNλ,μ.
ProofFor (u,v)∈Nλ,μ, by (2.1), (a+b)s≤2s-1(as+bs),s≥1, the Sobolev and H?lder inequalities, we have
This ends the proof due to 1 The character of the functions of the formKu,v:t→I(tu,tv) (t>0) and the Nehari manifold are closely related. Such functions are known as fibering maps, which were studied by Brown and Wu in [12]. If (u,v)∈E, we have Lemma 2.2Let (u,v)∈E{0,0} andt>0. Then (tu,tv)∈Nλ,μif and only ifK′u,v(t)=0, that is, the points on the Nehari manifold correspond to the critical points ofKu,v(t). In particular, (u,v)∈Nλ,μif andonly ifK′u,v(1)=0. ProofNote that Therefore, we can easily draw the conclusion of the lemma. Naturally, similar to the method used in Tarantello [24], we splitNinto three parts: It is easy to see that Thus, for each (u,v)∈Nλ,μ, we have (2.2) ProofUsing the same argument in [21], we omit the details here. Lemma 2.4One has the following. ProofThe proof is immediate from (2.2). ProofWe consider the following two cases. K″u,v(1)=(2-α-β)‖(u,v)‖2<0. and so (2.3) Similarly, using (2.2), the Sobolev and H?lder inequalities, we have which implies that (2.4) Combining (2.3) and (2.4) we obtain which is a contradiction. This completes the proof. In order to understand the Nehari manifold and fibering maps, we consider the functionφu,vdefined by Obviously, fort>0, (tu,tv)∈Nλ,μif and only if Note that Moreover, (2.5) and so we can see that if (tu,tv)∈Nλ,μ, then K″u,v(t)=tq+1φ′u,v(t). and clearlyφu,vis increasing on (0,tmax) and decreasing on (tmax,+∞) with limn→∞φu,v(t)=-∞. Moreover, it follows from (λ,μ)∈Θ that That is, for (λ,μ)∈Θ, (2.6) Therefore, we have the following lemma. and φ′u,v(t+)>0>φu,v(t-). Iλ,μ(t-u,t-v)≥Iλ,μ(tu,tv)≥Iλ,μ(t+u,t+v) for eacht∈[t+,t-] and Iλ,μ(t+u,t+v)≤Iλ,μ(tu,tv) for eacht∈[0,t+]. This completes the proof. Next, we remark that it follows from Lemma 5 that Then we have the following result. and so First, we will use the idea of Ni and Takagi [10] to get the following lemmas. Lemma 3.1If (λ,μ)∈Θ, then for every (u,v)∈Nλ,μ, there exist anε>0 and a differentiable functiong:Bε(0)×Bε(0)?E→R+such that g(0,0)=1,g(ω1,ω2)(u-ω1,v-ω2)∈Nλ,μ, ?(ω1,ω2)∈Bε(0)×Bε(0). Moreover, set then (3.1) for all (φ1,φ2)∈E. ProofWe defineF:R×E→R by it is easy to seeFis differentiable. SinceF(1,(0,0))=0 andFt(1,(0,0))=K″u,v(1)≠0, we apply the implicit function theorem at point (1,(0,0)) to get the existence ofε>0 and differentiable functiong:Bε(0)×Bε(0)→R+such thatg(0,0)=1 andF(g(ω1,ω2),(ω1,ω2))=0 for ?(ω1,ω2)∈Bε(0)×Bε(0). Thus, g(ω1,ω2)(u-ω1,v-ω2)∈Nλ,μ, ?(ω1,ω2)∈Bε(0)×Bε(0). Also by the differentiability of the implicit function theorem, for all (φ1,φ2)∈E, we know that Note that - andFt(1,(0,0))=K″u,v(1). So (3.1) holds. and (3.2) for all (φ1,φ2)∈E, whereE1,E2,E3is the same as in Lemma 3.1. Lemma 3.3If (λ,μ)∈Θ, then (i) there exists a minimizing sequence {(un,vn)}∈Nλ,μsuch that Proof(i) By Lemma 2.1 and the Ekeland variational principle [11] onNλ,μ, there exists a minimizing sequence {(un,vn)}?Nλ,μsuch that (3.3) and (3.4) Takingnlarge enough, from Lemma 2.7 we have from which we deduce that for large enoughn, which yields C1≤‖(un,vn)‖≤C2 (3.5) for suitableC1,C2>0. Now, we show that ‖Iλ,μ(un,vn)‖→0 asn→∞. Applying Lemma 3.1 with (un,vn) to obtain the functionsgn(ω1,ω2):Bεn(0)×Bεn(0)→R+for someεn>0, such that gn(0,0)=1,gn(ω1,ω2)(un-ω1,vn-ω2)∈Nλ,μ, ?(ω1,ω2)∈Bεn(0)×Bεn(0). gn(ω1,ρ,ω2,ρ)(un-ω1,ρ,vn-ω2,ρ)∈Nλ,μ, we deduce from (3.4) that By the mean value theorem, we have Thus, (3.6) It follows fromgn(ω1,ρ,ω2,ρ)(un-ω1,ρ,vn-ω2,ρ)∈Nλ,μand (3.6) that Hence we obtain (3.7) Note that ‖(gn(ω1,ρ,ω2,ρ)(un-ω1,ρ)-un,gn(ω1,ρ,ω2,ρ)(vn-ω2,ρ)-vn)‖ and If we letρ→0+in (3.7), then by (3.5) we can find a constantC>0, independent ofρ, such that We are done once we show that ‖g′n(0,0)‖ is uniformly bounded inn. By (3.1), (3.5) and the H?lder inequality, we have We only need to show that there exists aδ>0 such thatK″un,vn(1)≥δ>0 whennis large enough. On the contrary, assume that there exists a subsequence {(un,vn)}?Nλ,μsuch thatK″un,vn(1)=on(1). By (2.2) and the Sobolev inequality, we have and so (3.8) Similarly, using (2.2), the Sobolev and H?lder inequalities, we have which implies that (3.9) We obtain from (3.8) and (3.9) that for sufficiently largen. This is a contradiction. Hence we get This completes the proof of (i). (ii) Similarly, by using Lemma 3.2, we can prove (ii). We omit the details here. (ii) (u+,v+) is a solution of equation (1.1). ProofFrom Lemma 3.3, let {(un,vn)} be a (PS)αλ,μsequence forIλ,μonNλ,μ, i.e., Iλ,μ(un,vn)=αλ,μ+on(1),Iλ,μ(un,vn)=on(1) inE-1(Ω), (3.10) then it follows from Lemma 2.1 that {(un,vn)} is bounded inE. Hence, up to a subsequence, there exists (u+,v+)∈Esuch that (3.11) By the H?lder inequality and(3.11), we can infer that (3.12) and (3.13) First, we can claim that (u+,v+) is a nontrivial solution of (1.1). Indeed, by (3.10) and (3.11), it is easy to see that (u+,v+) is a solution of (1.1). Next we show that (u+,v+) is nontrivial. From (un,vn)∈Nλ,μ, we have (3.14) Letn→∞ in (3.14), we obtain which implies thatIλ,μ(u+,v+)=αλ,μand limn→∞‖(un,vn)‖2=‖(u+,v+)‖2. Noting that Iλ,μ(t+u+,t+v+) which is a contradiction. Finally, by Lemma 2.3 we obtain that (u+,v+) is a solution of (1.1). This completes the proof. (ii) (u-,v-) is a solution of equation (1.1). (3.15) then it follows from Lemma 2.1 that {(un,vn)} is bounded inE. Hence, up to a subsequence, there exists (u-,v-)∈Esuch that (3.16) By the H?lder inequality and (3.16), we can infer that and =||(un-u-,vn-v-)||2-f(|un|q-2un-|u-|q-2u-)(un-u-)dx then we can deduce that ‖(un-u-,vn-v-)‖→0 asn→∞. which implies that (u-,v-) is nontrivial. Finally, we obtain and by Lemma 2.3 (u-,v-) is a solution of (1.1). This completes the proof.






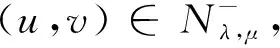

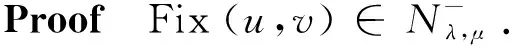

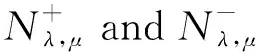



3 Proof of Theorem 1.1
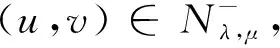

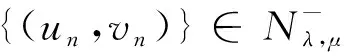

≤ρ|gn(ω1,ρ,ω2,ρ)|+|gn(ω1,ρ,ω2,ρ)-1|‖(un,vn)‖





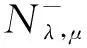





 數(shù)學(xué)理論與應(yīng)用2020年2期
數(shù)學(xué)理論與應(yīng)用2020年2期
