HIGHER-ORDER NON-SYMMETRIC DUALITY FOR NONDIFFERENTIABLE MINIMAX FRACTIONAL PROGRAMS WITH SQUARE ROOT TERMS?
SONALIVikas SHARMA Navdeep KAILEY
School of Mathematics,Thapar Institute of Engineering and Technology,Patiala,India
E-mail:sethisonali22@gmail.com;vikas.sharma@thapar.edu;nkailey@thapar.edu
Abstract In this paper,we emphasize on a nondifferentiable minimax fractional programming(NMFP)problem and obtain appropriate duality results for higher-order dual model under higher-order B-(p,r)-invex functions.We provide a nontrivial illustration of a function which belongs to the class of higher-order B-(p,r)-invex but not in the class of second-order B-(p,r)-invex functions already existing in literature.An example of finding a minimax solution of NMFP problem by using higher-order B-(p,r)-invex functions has also been given.Various known results are discussed as particular cases.
Key words nonlinear programming;higher-order duality;fractional programming;minimax programming;B-(p,r)-invexity
1 Introduction
In the primitive duality theory,the duality theorems are generally based on convexity suppositions,which are restrictive in applications.There exists a number of optimization problems in the literature which are nonconvex and hence difficult to analyze.To relax convexity suppositions applied on the involved functions,various generalized notions were constructed which are bene fi cial to prove duality theorems for such optimization problems.Antczak[1]gave the concept of p-invex sets and(p,r)-invex functions and obtained sufficient conditions for a nonlinear programming problem involving(p,r)-invex functions.Further generalization of(p,r)-invex functions was studied by Antczak[2]as B-(p,r)-invex functions.
A prominent class of mathematical programming problems is fractional programming that handles the situations where a ratio of two mathematical functions is either maximized or minimized.Fractional programming(FP)is one of the most popular field in nonlinear optimization theory.
In the past years,numerous researchers worked on nondifferentiable minimax fractional programming(NMFP)problems.A large number of applications of minimax fractional programming problems can be seen in formulation of discrete and continuous rational approximation problems with respect to the Chebyshev norm[3],continuous rational games[4],multiobjective programming[5]and in the design of electronic circuits.Liu[6]obtained the secondorder duality theorems for minimax problem under generalized second-order B-invex functions.Parameter-free dual models for NMFP problems were constructed by Lai and Lee[7]and duality theorems were proved under pseudo/quasi-convex functions.Various results of optimality and duality for generalized FP problem were explored by Liang and Shi[8]under generalized convexity.Mishra and Rueda[9]and Ahmad et al.[10]studied the second-order duality results for the nondifferentiable minimax programming(NMP)problems.Gupta et al.[11]also obtained second order duality relations for NMFP problems using type-I functions.
The notion of higher-order duality was initiated by Mangasarian[12].Higher-order duality plays a vital role because of computational importance.It gives higher bounds whenever an approximation is used.Suneja et al.[13]considered higher-order Mond-Weir and Schaible type nondifferentiable dual programs and their duality theorems under higher-order(F,ρ,σ)-type I assumptions.Various higher-order duality models for nondifferentiable minimax problem were derived by Jayswal and Stancu-Minasian[14].Later on Jayswal et al.[15]has taken NMFP problem and established duality theorems for relating the results of primal and dual problems under generalized convexity.Optimality conditions and duality relations for multiobjective programming problems were introduced by Dubey et al.[16].Sonali et al.[17]obtained secondorder duality results for NMFP problem under second-order B-(p,r)-invexity.Jayswal et al.[18]corroborated a higher-order dual model for NMFP problem under(C,α,ρ,d)-convexity.Recently Li et al.[19]derived optimality conditions and duality results for minimax fractional programming problems with data uncertainty.
The paper is structured as follows.In Section 2,a novel concept of higher-order B-(p,r)-invex functions is introduced.An illustration showing the existence of higher-order B-(p,r)-invex functions has been given.Optimality conditions for NMFP problems are also discussed.Section 3 presents a higher-order dual model for NMFP problem.A numerical example of NMFP program has been solved in Section 4.The paper closes with conclusions in Section 6.
2 Notations and Preliminaries
In this section,we study the following NMFP problem

where Y is a compact subset of Rl′, ζ(·,·):Rn×Rl′→ R, ?(·,·):Rn×Rl′→ R are C2(twice continuously differentiable)functions on Rn×Rl′and ξ(·):Rn→ Rmis C2function on Rn.G and N are n×n positive semide finite(PS)matrices.We assume that ?(s,y)?(sTNs)1/2>0 and ζ(s,y)+(sTGs)1/2≥0 for each(s,y)∈×Y,where={s∈Rn:ξ(s)≤0}denote the set of all feasible solutions of NMFP.
For each(s,y)∈?X×Y and M={1,2,···,m},we de fine


Since ζ and ? are C2and Y is compact in Rl′,it follows that for each s?∈,Y(s?)6=φ,and for any∈Y(s?),we have a positive constant
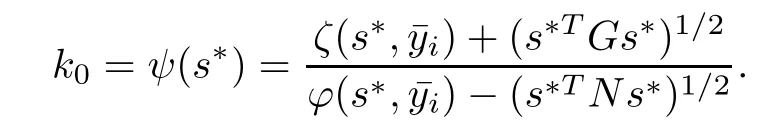
De finition 2.1Let ζ:→R(where?Rn)be a differentiable function and let p,r be arbitrary real numbers.Then ζ is said to be higher-order B-(p,r)-invex(strictly higher-order B-(p,r)-invex)with respect to η,b and a differentiable function k:×Rn→R(?Rn)at a∈if there exists a function η:→Rnand a function b:→R+such that for all s∈and l∈Rn,the following inequalities holds

We note that
(i)if r 6=0,p=0 in(2.1),then
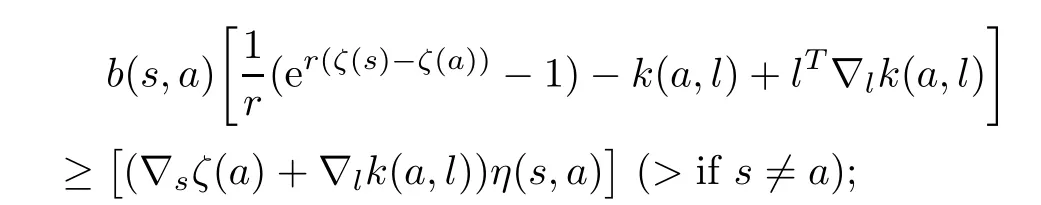
(ii)if p 6=0,r=0 in(2.1),then
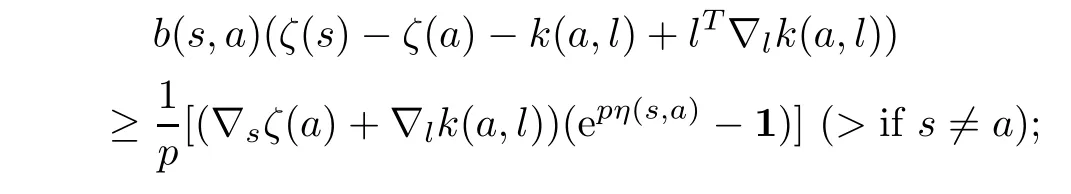
(iii)if r=0,p=0 in(2.1),then

where 1=(1,1,···,1)∈ Rn,(epη(s,a)? 1)stands for the n-vector(epη1(s,a)? 1,epη2(s,a)? 1,···,epηn(s,a)? 1).
Lemma 2.2(Generalized Schwartz inequality[20]) Let G be a positive semide finite matrix of order n.Then,for all s,w∈Rn,
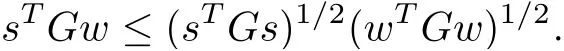
The equality holds if Gs= λGw for some λ ≥ 0.
Example 2.3LetS=[0.1,1]?R.Consider the function ζ:→R de fined by
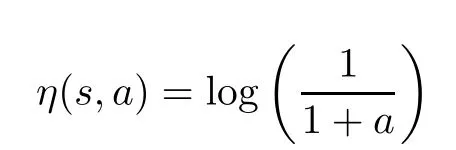
and
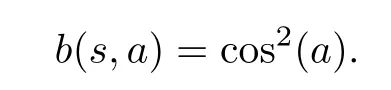

for all s,a∈?S as can be seen from Figure 1.
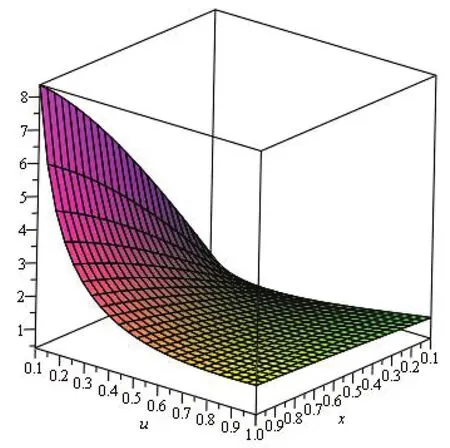
Figure 1 graph of function
But it is not second order B-(?1,?1)-invex as
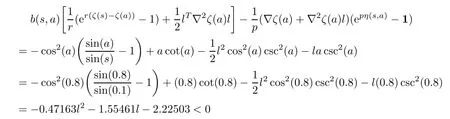
for s=0.1,a=0.8 and l∈R.
Therefore the function ζ is higher-order B-(1,1)-invex function but not second order B-(?1,?1)-invex.
Remark 2.4All the results in this paper will be discussed only in the case p 6=0,r 6=0.The proofs are easier than this in the other cases.It follows from the form of inequalities which are given in De finition 2.1.Moreover,without limiting the generality considerations,we shall suppose that r>0.
Theorem 2.5(Necessary Condition) If s?is an optimal solution of NMFP problem satisfying s?TGs?>0,s?TNs?>0,and ?ξj(s?),j ∈ J(s?)are linearly independent(LI),then there exist(q,t?,)∈K(s?),k0∈R+,w,v∈Rnandμ?∈such that
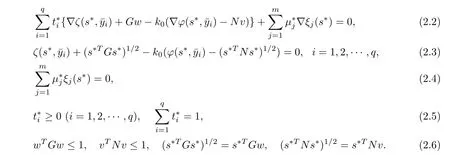
In the above theorem,both matrices G and N are positive de finite.If either s?TGs?or s?TNs?is zero or both are zero,then the functions involved in the objective of problem NMFP are not differentiable.To construct necessary conditions for these cases,for(q,t?,)∈K(s?),we de fine
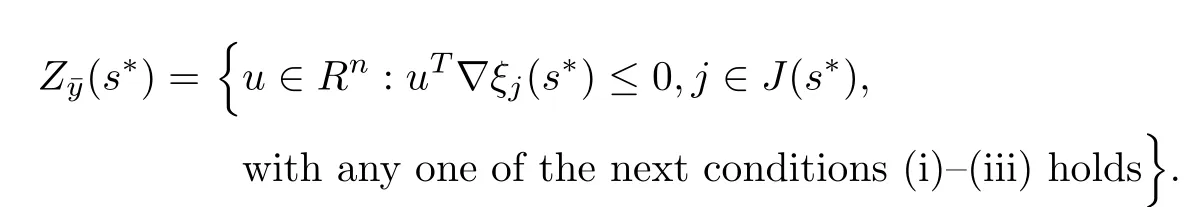
(i) s?TGs?>0, s?TNs?=0
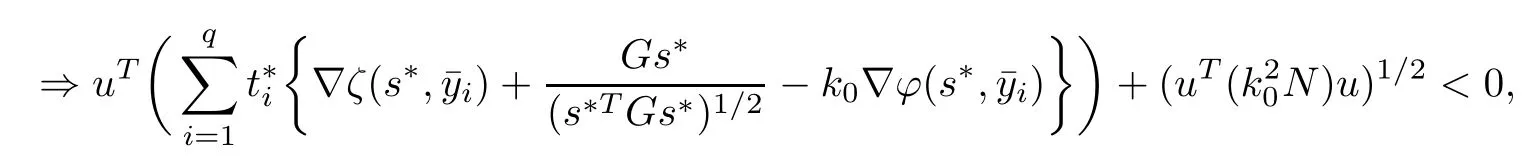
(ii) s?TGs?=0, s?TNs?>0

(iii) s?TGs?=0, s?TNs?=0
Theorem 2.6(Sufficient Condition) Let s?be a feasible solution of NMFP and there exist a positive integer q,1≤q≤n+1,t?∈,∈Y(s?)(i=1,2,···,q),k0∈R+,w,v∈Rnand μ?∈satisfying relations(2.2)–(2.6).Assume that
(ii) ν(s?,l?)≥ 0 and ?lν(s?,l?)=0.
Then,s?is an optimal solution of problem NMFP.
ProofSuppose s?is not an optimal solution of NMFP.Then there exists anˉs∈?X such that
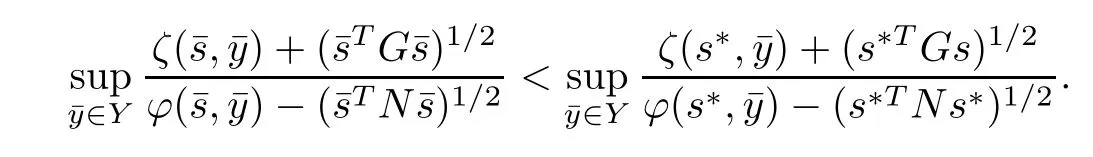
Since


therefore,we get
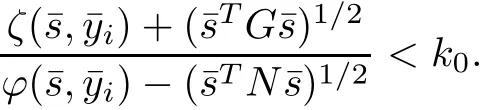
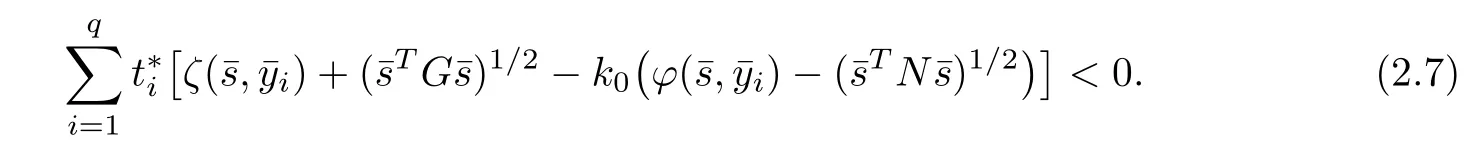
Using Lemma 2.2,(2.6),and(2.7),we obtain
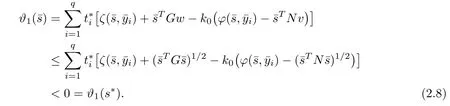
As ?(.)is higher-order B-(p,r)-invex at s?onwith respect to η and b,we have

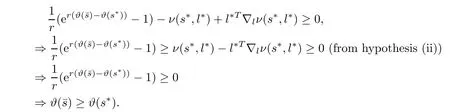
Now

For our convenience,Assume that
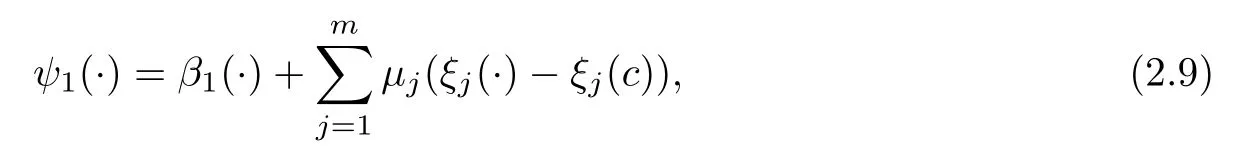
where
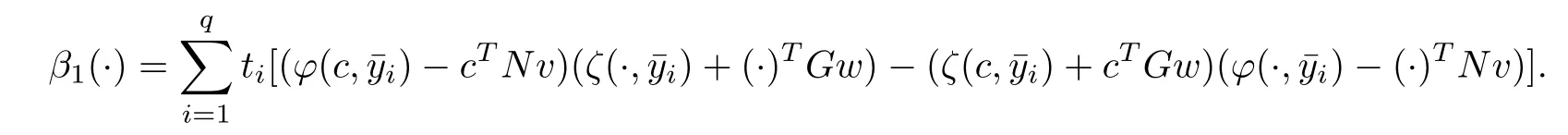
3 Duality Results
Duality theory is well-developed for nonlinear programming problems.It will be interesting to extend the second order results to the higher-order as it provides tighter bounds when approximations are used.A uni fied higher-order dual model for NMP was constructed by Ahmad et al.[21]under higher-order(F,α,ρ,d)-Type I suppositions which was the extension of second-order duality results given by Mishra and Rueda[9].Later Ahmad[22]discussed higher-order duality for NMFP problem using generalized convexity assumptions.In this paper,we have considered a higher-order dual model for NMFP problem.
Model-I
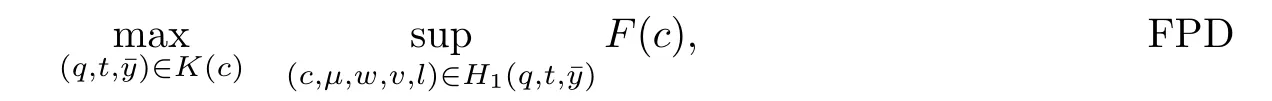

If H1(q,t,)=φ,then the supremum of F(c)over H1(q,t,)will be?∞.
Now,we acquire the following duality results.
Theorem 3.1(Weak duality)Let s and(c,μ,w,v,q,t,,l)be feasible solutions of NMFP and FPD,respectively.Suppose that
(i) ψ1(·)is higher-order B-(p,r)-invex function at c with respect to η and b satisfying b(s,c)>0 for all s∈,
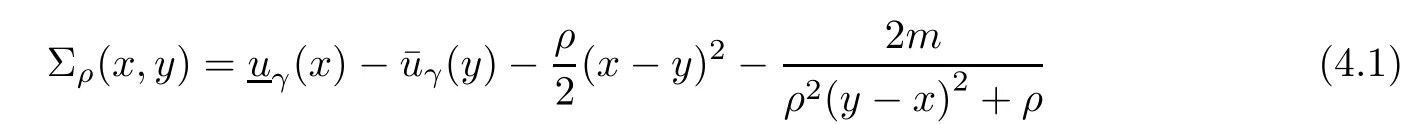

ProofContrary to the result assume that
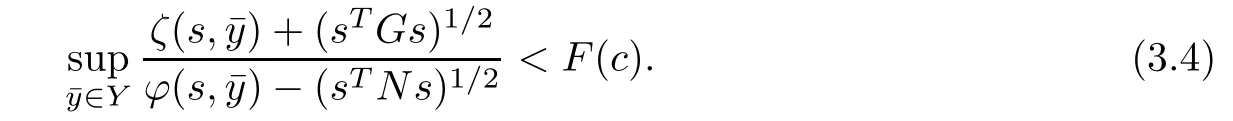
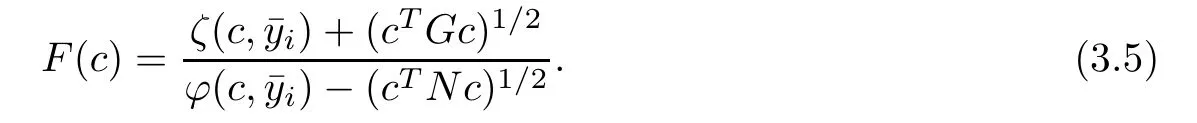
From(3.4)and(3.5),for i=1,2,···,q,we get
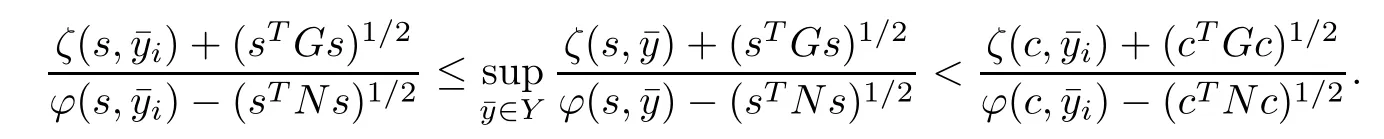
Also from ti≥0,i=1,2,···,q,t 6=0 and∈Y(c),we get
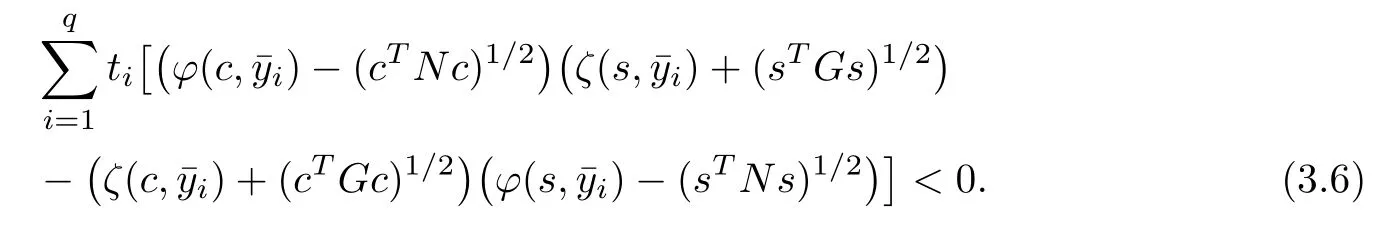
Now
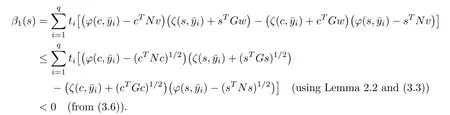
Therefore

Since ψ1(·)is higher-order B-(p,r)-invex function at c,therefore,we have
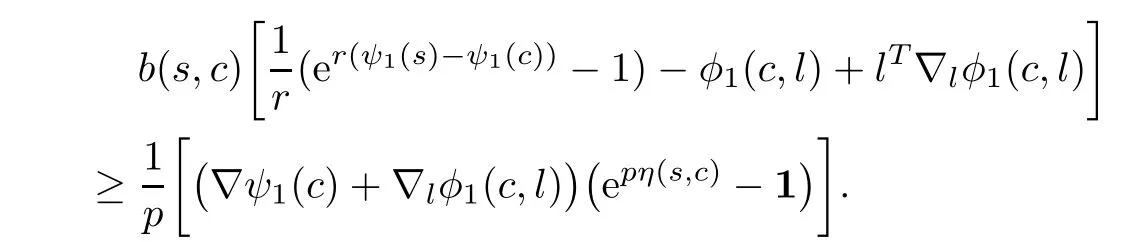
From above,b(s,c)>0 and(3.1),we have
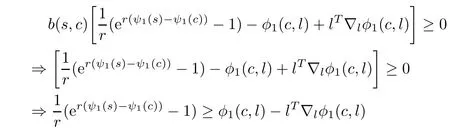

Now

Therefore β1(s)≥ 0.This contradicts(3.7),hence the result.
Theorem 3.2(Strong duality) Let s?be an optimal solution for NMFP and let?ξj(s?),j ∈ J(s?)be LI.Assume that

Then there exist(q?,t?,)∈K(s?)and(s?,μ?,w?,v?,l?=0)∈H1(q?,t?,)such that(s?,μ?,w?,v?,q?,t?,,l?=0)is feasible solution of FPD and the two objectives have same values.If,in addition,the assumptions of Theorem 3.1 hold for all feasible solutions(s,μ,w,v,q,t,ˉy,l)of FPD,then(s?,μ?,w?,v?,q?,t?,,l?=0)is an optimal solution of FPD.
ProofSince s?is an optimal solution of NMFP and ?ξj(s?),j ∈ J(s?)are LI,then by Theorem 2.5,there exist(q?,t?,ˉy?)∈K(s?)and(s?,μ?,w?,v?,l?=0)∈H1(q?,t?,)such that(s?,μ?,w?,v?,q?,t?,,l?=0)is feasible solution of FPD and the two objectives have same values and

Optimality of(s?,μ?,w?,v?,q?,t?,ˉy?,l?=0)for FPD,thus follows from Theorem 3.1.
De finition 3.3(Strict converse duality) Let s?be an optimal solution for NMFP and(c?,μ?,w?,v?,q?,t?,ˉy?,l?)be an optimal solution to FPD.Assume that
(i) ψ1(·)is strictly higher order B-(p,r)-invex at c?with respect to η and b satisfying b(s,c?)>0 for all s∈?X,
(ii){?ξj(s?),j ∈ J(s?)}are LI,
(iii) φ1(c?,l?)=l?T?lφ1(c?,l?).
Then c?=s?.
ProofSince ψ1(.)is strictly higher-order B-(p,r)-invex at c?,we have
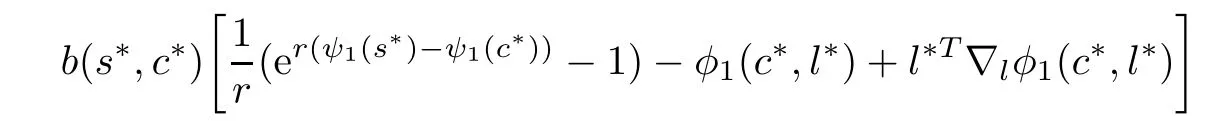
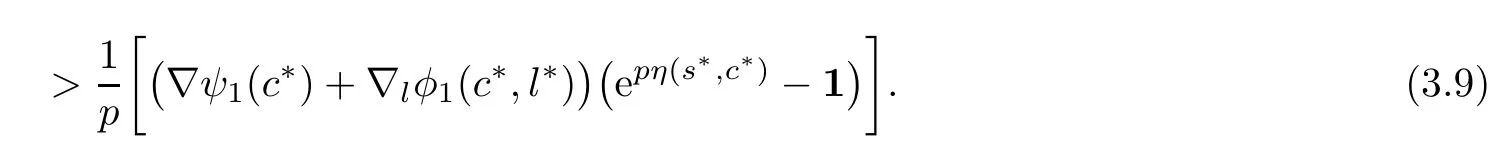
Using(3.1)and hypothesis(iii)in(3.9),we get
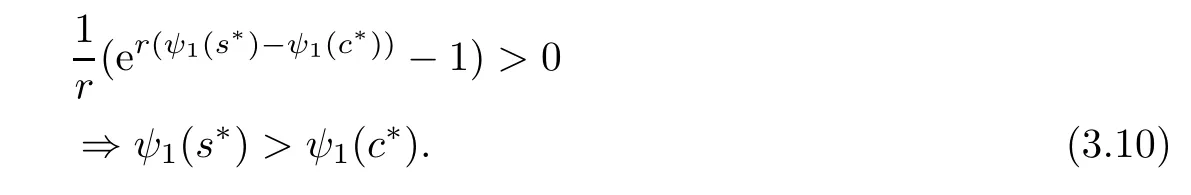
Now
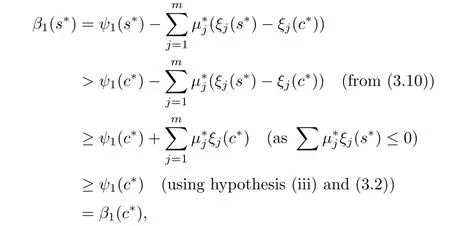
that is,

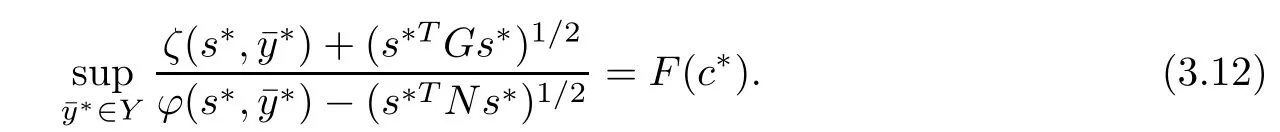
By(3.12)and(3.13),we get
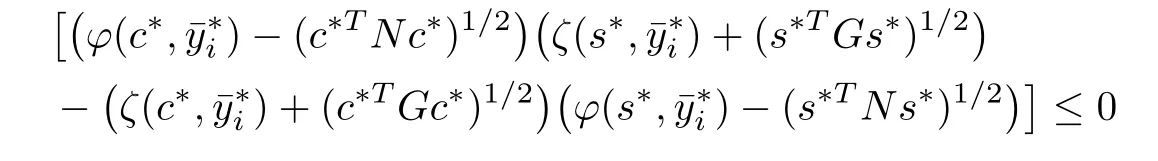
for all i=1,2,···,q?and∈Y.From∈Y(c?)?Y and t?∈Rwith,we obtain
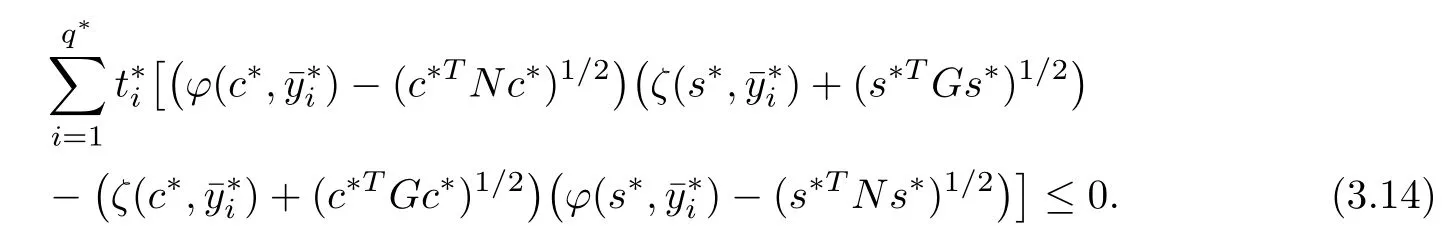
From Lemma 2.2,(3.3),and(3.14),we have


which contradicts(3.11),hence the result.
4 Example of a Minimax Problem
Let n=l′=1,m=2 and Y=[1,2].
Let ζ(s,y)=s4+2s2y+y, ?(s,y)=s2+4,G=N=1,ξ1(s)=s?3 and ξ2(s)= ?s+1.
Also ξ(s)≤0 ?s?3≤0 and?s+1≤0,

Therefore

Now

and
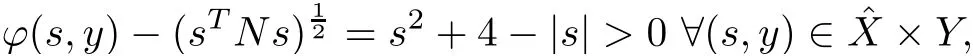
where

Now the problem NMFP becomes
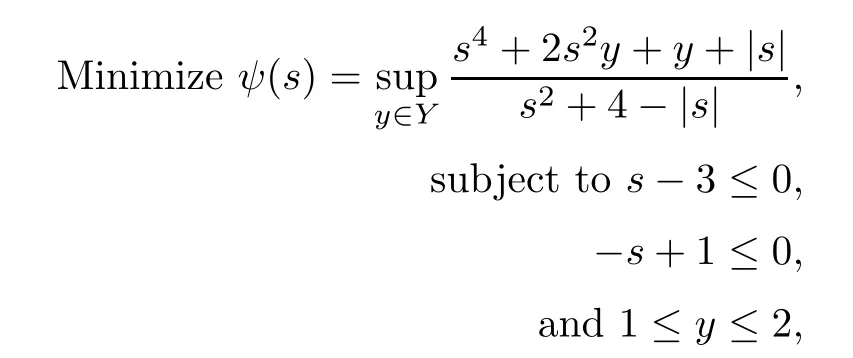
here Y(s)={2}and K(s)={(1,1,2)}.
In order to find a minimax solution of NMFP for s?∈ [1,3],we have considered the following cases.
Case 1Take s?=3.Using(2.3),(2.5)and(2.6),we get k0=12.2,w=v=1 and=1.
Since ξ1(s?)=0 for s?=3,therefore from(2.4),we haveξ2(s?)=0 which implies=0.Hence from(2.2),= ?72 does not satisfy the condition that μ?1∈ R+.
Case 2Take 1 that is, that is,2s?5? 3s?4+16s?3? 5s?2+28s?+6 ≤ 0,which is not possible for any s?∈ (1,3). Therefore s?∈ (1,3)cannot be a minimax solution. Case 3Take s?=1. Since ξ2(s?)=0 for s?=1,therefore from(2.4),we have(s?)=0 implies=0 and using(2.5),we get=1.By solving(2.3),we have k0=2 and using(2.6),we obtain w=v=1.Putting these values in(2.2),we get=11.Now using w=v=1 along with=1,k0=2,=0 and=11,we can check that all these values satisfy the necessary conditions for a minimax solution.Therefore s?=1 is the only candidate for a minimax solution. Now we will justify that s?=1 is an optimal solution of NMFP.For this we will show that ?(·)is higher-order B-(p,r)-invex function at s?.Here Using w=v=1,k0=2 and=0 and=11,we get which is convex and hence higher-order B-(p,r)-invex function at s?=1.By taking q=1,=1,w=v=1,k0=2,=0 and=11,the sufficient conditions of the theorem are easily veri fied and s?=1 is a minimax solution. Now we will formulate dual model FPD for NMFP problem.Let φ1(c,l)=(c+1)l.From FPD,we have (i)If we take φ1(c,l)=lT?2ψ1(c)l in FPD then,our dual model will be reduced to the second order dual model given by Gupta et al.[20]. (ii)If l=0,then the dual model FPD reduces to the problems studied in[7,23,24]. (iii) If l=0 and G and N are zero matrices of order n,then FPD becomes the dual problem given in[25,26]. In the present work,we have formulated a higher-order dual model for NMFP problem and proved duality results under higher-order B-(p,r)-invexity.An example of a higher-order B-(p,r)-invex function has been given.Also we have solved a NMFP problem using optimality conditions.
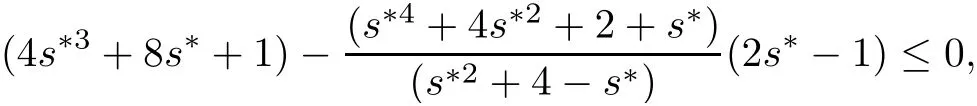

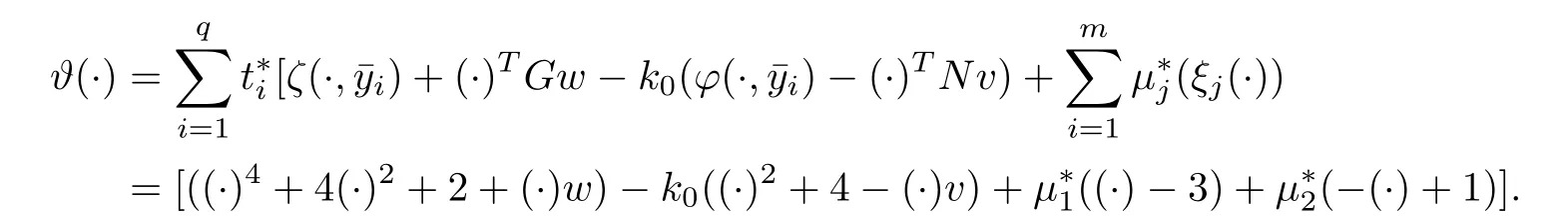
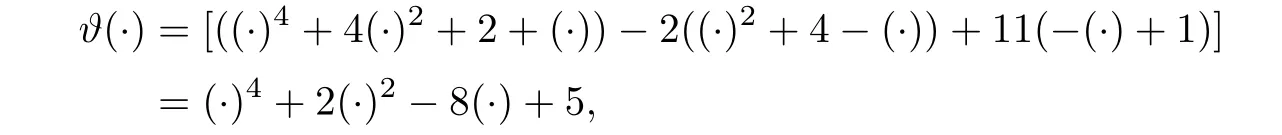

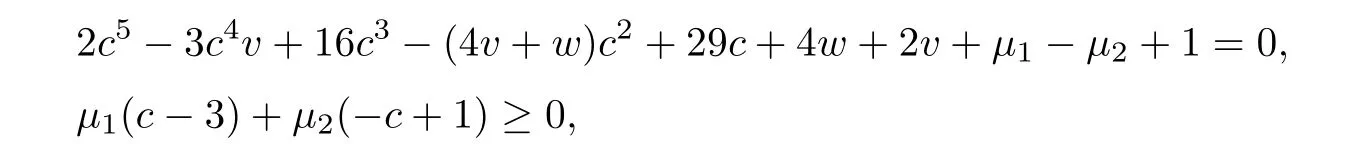
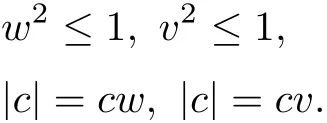
5 Special Cases
6 Concluding Remarks
 Acta Mathematica Scientia(English Series)2020年1期
Acta Mathematica Scientia(English Series)2020年1期
- Acta Mathematica Scientia(English Series)的其它文章
- BOUNDEDNESS OF MULTILINEAR LITTLEWOOD-PALEY OPERATORS ON AMALGAM-CAMPANATO SPACES?
- GLOBAL SIMPLE WAVE SOLUTIONS TO A KIND OF TWO DIMENSIONAL HYPERBOLIC SYSTEM OF CONSERVATION LAWS?
- COMPLEX INTERPOLATION OF NONCOMMUTATIVE HARDY SPACES ASSOCIATED WITH SEMIFINITE VON NEUMANN ALGEBRAS?
- THE ENERGY CONSERVATIONS AND LOWER BOUNDS FOR POSSIBLE SINGULAR SOLUTIONS TO THE 3D INCOMPRESSIBLE MHD EQUATIONS?
- EXISTENCE OF SOLUTIONS OF nTH-ORDER NONLINEAR DIFFERENCE EQUATIONS WITH GENERAL BOUNDARY CONDITIONS?
- HERMITIAN-EINSTEIN METRICS FOR HIGGS BUNDLES OVER COMPLETE HERMITIAN MANIFOLDS?
