Yonggan LIANG (梁勇敢),Jian WU (吳健),Hui LI (李輝),3,Ruihuan TIAN (田瑞煥),Chengxun YUAN (袁承勛),Ying WANG (王瑩),Zhongxiang ZHOU (周忠祥) and Hao TIAN (田浩)

1 School of Physics,Harbin Institute of Technology,Harbin 150001,People’s Republic of China

2 National Key Laboratory of Electromagnetic Environment (LEME),China Research Institute of Radio Wave Propagation,Beijing 102206,People’s Republic of China

3 Authors to whom any correspondence should be addressed.

Abstract

Keywords:glow discharge,dusty plasma,kinetic model,transport coefficient,ionization rate coefficient

1.Introduction

Dusty plasma is usually defined as a partly ionized gas containing dispersed micro-sized particles with large negative charge.The plasma properties will change when dust particles are introduced since the dust particles serve as an additional sink of electrons and ions.In the last few decades,dusty plasma is of great interest in many different fields,such as formation of cosmic clouds[1,2],technological plasma processes [3–5],fusion related researches [6–8],and so on.

Under laboratory conditions,dusty plasma is widely studied in direct current (DC),radio frequency (RF) and microwave(MW) discharges due to their importance in fields like plasma chemistry,thin film deposition,plasma etching,and so on[9–12].The hydrodynamic models are usually employed to describe these discharge dusty plasmas,in which the electrons and ions are assumed to be in Maxwellian equilibrium [5,13–15].With the assumption of Maxwellian equilibrium,the electron transport and ionization rate coefficients that are of great significance for simulating these discharge processes are obtained and used in these hydrodynamic models[16,17].However,as we know that for most of low-temperature plasmas,their electron energy distribution functions (EEDFs) will always deviate from the Maxwellian distribution to a certain extent because of many kinds of electron collisions[18,19].Also,it has been proven that plasma EEDFs can be affected by dust particles too [11,20].It means that,under some discharge conditions,inaccurate electron transport(mobility and diffusion)and ionization rate coefficients will be obtained by the use of Maxwellian distribution,since these parameters are directly related to the EEDFs.

Though the influence of dust particles on plasma EEDFs has been studied by many researchers[11,21–23],the most used simplification method in these studies is still the local approximation.While the local approximation is not always valid for some discharge conditions,especially for the relatively low gas pressure [24].For the glow discharge plasmas in a cylindrical tube,the local approximation is applicable only if the inequality R/2.4?λεis satisfied[25],where R is the tube radius,R/2.4 is the characteristic diffusion length,and λεis the electron energy relaxation length.In gas discharge dusty plasma,the value of λεmainly depends on the EEDF,gas pressure,dust density,size,and so on.When the inequality R/2.4?λεcannot be satisfied,the nonlocal approach [26]is usually a preferred method to simplify the Boltzmann equation to obtain more accurate EEDF profiles and corresponding plasma parameters.

In this paper,the local approximation and nonlocal approach are employed respectively to simplify the Boltzmann equation to compare their difference.The detailed model description is presented in section 2.The EEDFs are obtained by simultaneously solving the simplified kinetic equations and the dust charging equations.The finite difference method(FDM)is employed to conduct the calculation procedure.Then the electron transport (mobility and diffusion) and ionization rate coefficients are calculated on the basis of the obtained EEDFs.The calculation results and analysis are shown in section 3.Finally,the conclusion is presented in section 4.

2.Model description

In this paper,the kinetic models based on the local approximation and nonlocal approach are developed for dusty plasma in positive column of argon DC glow discharge.The electron–dust collisions are considered in the kinetic equation as additional collision terms.Electron and ion charging currents are calculated by the orbital motion limited (OML) method and collision enhanced collection(CEC)approximation.The cross sections of electron scattering (elastic collision) and collection (inelastic collision) by dust particles are deduced from the dust surface potential.Then the electron transport(mobility and diffusion)and ionization rete coefficients are calculated according to the EEDFs and total electron momentum transfer frequency.

2.1.Electron kinetic equations

The EEDF of plasma is usually deduced from the Boltzmann equation that expressed as

where feis the electron velocity distribution function(EVDF);v is the electron velocity;e is the electron elementary charge;merepresents the electron mass;E is the electric field;andrepresents the electron collision terms.

Usually,the anisotropy part of the EVDF is very low compared with its isotropy part.So the EVDF can be well represented by the two-term approximation,which expands the EVDF to first order in a small deviation from isotropy,and it is expressed as

Using the two-term approximation,and taking the electron kinetic energy u (u=mev2/(2e)) as variable instead of v,the Boltzmann equation (1) can be simplified as a second-order partial differential equation (see equation (3)) to describe the isotropic part of dusty plasma EEDF f0[27]

Here,νm=(ngσea+ndσed)v is the total electron momentum transfer frequency;ngand ndare neutral atom number density and dust density;σeaand σedrepresent the electron–neutral and electron–dust momentum transfer cross sections.Sea(f0)represents the electron-atom collision terms.Note that electron–dust collisions have been considered as additional collision terms Sed(f0) in equation (3).For discharges with relative high pressure (usually judged byfor glow discharge in a cylindrical tube),the electrons collide strongly with other particles,and the electron energy variations caused by the spatial inhomogeneity are negligible compared with the collision terms and energy diffusion.In this situation,the local approximation that neglects all spatial gradient terms is applicable for simplifying equation(3).The corresponding local kinetic equation is deduced as

On the other hand,if the gas pressure is low(usually judged byfor glow discharge in a cylindrical tube),the spatial gradient terms can be important to the EEDF and the local approximation will not be applicable any more.In this case,the nonlocal approach should be used to simplify equation(3).In the nonlocal approach,the total electron energy ε=u+Φ(r) is used to replace kinetic energy u as variable of EEDFs,where Φ(r)is the potential in radial direction.Then the corresponding nonlocal kinetic equation can be deduced as

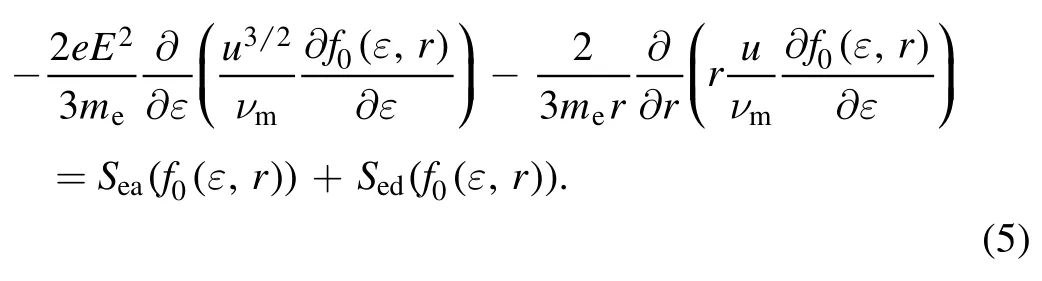
To solve the nonlocal kinetic equation(5)in an easier form,it is further simplified by spatially averaging over the radial path that electrons can reach [26,28].In this way,the nonlocal kinetic equation is finally approximated as follow

The averaged terms in equation (6) are determined by equation (7)

where Uwis the absolute value of the tube wall potential.The integral upper limit r(ε) in equation (7) is calculated from equation (8)

The radial potential distribution Φ(r) of dust-free and dusty plasma is estimated with the fluid model developed in[29].The presence of dust particles can reduce the absolute value of radial potential,which will influence the EEDF profiles to some extent.

2.2.Dust charging processes

Dust particles in glow discharge plasma are usually negatively charged since electron velocity is much higher than ion velocity.The dust particle charge number and surface potentials are determined by the charging currents balance equation.The OML theory [30]is the most widely used model to estimate the electron charging current of dust particles,which is derived as

Here,neis electron density;rdand φsare radius and surface potential of dust particles,respectively.

As for the ion charging process,the CEC approximation[31]is employed to estimate the corresponding charging current since the ion-neutral collisions may have a significant influence on the ion charging process.The ion velocity distribution is usually assumed to be Maxwellian,then the ion charging current can be deduced as

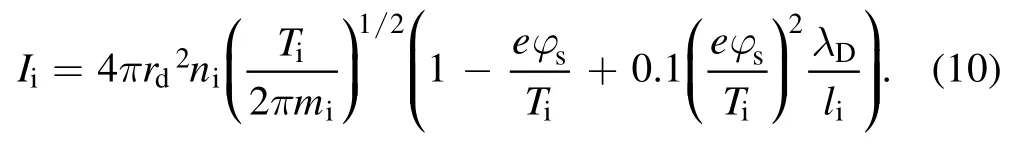
Here,niis ion density;Tirepresents ion temperature;miis the ion mass;λDis the Debye length of dusty plasma;liis the ion mean free path.Then the charging currents balance equation can be expressed as

Combining the electroneutrality condition for dusty plasma

where|Zd|is charge number of dust particle,which is usually determined by dust radius and dust surface potential.The surface potential of dust particles can be obtained by solving equations (11) and (12).

2.3.Electron collisions terms for the kinetic equation

Generally speaking,in glow discharge plasma,the electron–electron collision can be neglected when calculating the EEDF profiles under ionization degree β＜10?5(β=ne/ng)[32].Under calculation conditions used in this paper,the ionization degree β is less than 10?6(see the results and discussion part),so the electron–electron collision is not considered.Then,only electron–neutral and electron–dust collisions are considered in this study.

The electron–neutral collision consists of two parts:elastic and inelastic collisions.For electron–neutral elastic collision,its corresponding collision term is expressed as

whereis the elastic collision frequency of electron-atom.

As for the electron–neutral inelastic collision,it can be divided into two main parts corresponding to excitation and ionization processes.The different level of electron excited and ionized states can be reduced as a single electronic state to simplify the calculation in gas discharge plasma[33].Then the corresponding excitation and ionization collision terms are written as follows

whereandare excitation and ionization collision frequencies;Uexand Uiare excitation and ionization threshold energy,and which are set as 11.72 eV and 15.6 eV,respectively,for argon plasma.The electron–neutral cross sections are from [34].

The electron–dust collisions consist of the electron scattering(elastic collision)and collection(inelastic collision)processes by dust particles,and their corresponding collision terms are shown below [11]

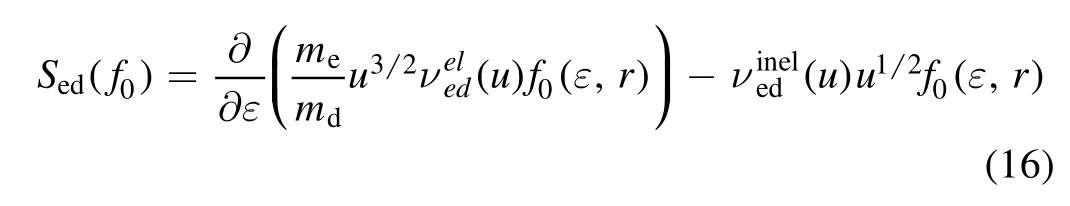
where md=(4/3)πrd3ρdis dust particle mass,and dust material density is set as ρd=3 g cm?3in this study,is the electron–dust momentum transfer frequency andis electron collection frequency.In dusty plasma,the cross section of electron–dust momentum transfer can be expressed as [35]

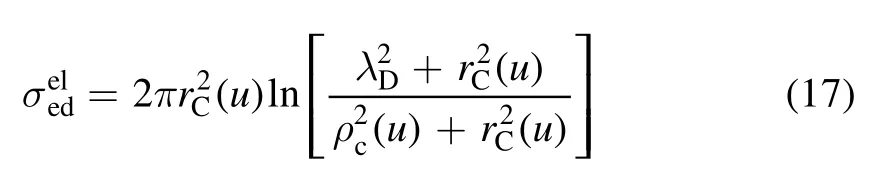
where rC(u) is defined as Coulomb radius of electron–dust collision and is calculated by rC(u)=rdeφs/(2u);ρc(u) corresponds to the maximum impact parameter in collection process,which is defined as

The electron–dust collection cross section is expressed as[35]

With the electron–neutral and electron–dust collision terms described above,the nonlocal kinetic equation (6) can be written in detail as

2.4.The transport and ionization rate coefficients for dusty plasmas

The transport and ionization rate coefficients are of crucial importance for simulating the gas discharge process and they are calculated based on the plasma EEDFs.The electron mobility μeand diffusion coefficient Defor dusty plasma are given by [36]

Many kinds of coefficients are defined to calculate the reaction rates appearing in the source terms of fluid equations.The most straightforward one is to define the corresponding rate coefficients as follow [36]

where σiis electron-atom ionization cross section.From equations (21)–(23),it can be seen that electron mobility,diffusion and ionization rate coefficients are all calculated based on the EEDF.Dust particles can influence these parameters by influencing the total electron momentum transfer frequency and EEDF profiles.

3.Results and discussion

The normalized local and nonlocal EEDFs are calculated by solving the corresponding kinetic equations (4) and (6)numerically.The kinetic equations are solved by using the finite-difference method.Then the electron effective temperature,electron mobility and diffusion coefficient,and ionization rate coefficient are obtained and analyzed according to the obtained EEDFs.These calculations are simultaneously carried out for dust-free and dusty plasmas to analyze the influence of dust particle on these parameters.The calculation is performed in the positive column of argon DC glow discharge.Detailed calculation conditions are presented as:discharge tube radius R=1 cm,gas pressure P=0.5 torr,gas density ng=1.7×1016cm?3,ion density ni=1010cm?3,gas and ion temperature Tg=Ti=300 K (0.026 eV),dust radius rd=1 μm and dust density nd=106cm?3for dusty plasmas.Note that,with the calculation conditions listed above,the ratio R/(2.4λε)is estimated to be smaller than one for dust-free and dusty case,which means that the nonlocal kinetic model is more appropriately to calculate and analyze the plasma properties.The main calculation results of the presented model are shown in the following figures 1–7.

The local and nonlocal EEDF results of dust-free and dusty plasma are shown in figures 1 and 2.It can be seen that,for dust-free plasma,the population of the high energy component of the nonlocal EEDF is enhanced compared with that part of local EEDF since the use of averaged collision terms in nonlocal kinetic equation leads to a lower electron collision frequency.The difference can substantially influence the calculated values of the rate coefficients for the excitation and ionization reactions with high threshold energies.Meanwhile,from figure 1 we can see that the local and nonlocal EEDFs clearly deviate from their original profiles(the dust-free ones) with nd=106cm?3when the axial electric field is low.The introduction of dust particles decreases the energetic electron number and increases the low energy electron number due to the collection of high energy electrons by negatively charged dust particles and energy loss caused by electron–dust momentum transfer collisions.With the increase of the axial electric field (see figure 2),the influence of dust particles on the EEDFs becomes less noticeable since the averaged electron energy becomes higher and the proportion of the high energy electron collected by dust particle is reduced.Note that the difference between nonlocal dust-free and dusty EEDFs is larger than the difference between local cases,because the radial potential used for dusty plasma is different with the dust-free case in their nonlocal kinetic models.

Figure 1.The local and nonlocal EEDFs of dust-free and dusty plasmas for E=5 V cm?1.

Figure 2.The local and nonlocal EEDFs of dust-free and dusty plasmas for E=15 V cm?1.

Figure 3.The dependence of ratio nd|Zd|/ne on axial electric field E.

Figure 4.Effective electron temperature as function of axial electric field E.

Figure 3 presents the dependence of ratio nd|Zd|/neon axial electric field E.It can be seen that the ratio nd|Zd|/neincreases with the increasing axial electric field since the averaged electron energy increases with the increasing axial electric field.The ratio nd|Zd|/neis always smaller than 1,which means that the electron density does not decrease much when dust particles are introduced.

The effective electron temperature defined as=Teffis illustrated in figure 4.The effective electron temperature increases with the increasing axial electric field,because more energy is injected by the axial electric field.The effective electron temperature Teffobtained from the nonlocal model is higher than that from the local model,since averaged collision terms in the nonlocal kinetic equation leads to a lower electron collision frequency and electrons lose less energy through collisions.With the increase of axial electric field,the increase of Teffcalculated from nonlocal model should be higher than the local case to hold the energy balance between electric field and electron–neutral collisions.When dust particles are introduced,the decrease of Teffin nonlocal model is more obvious compared with the local case since the high energy electron proportion in nonlocal EEDFs is higher.With the increase of the electric field,the influence of dust particles on the Teffbecomes less noticeable since the effect of dust particles on EEDFs becomes smaller.

Figure 5.Dependences of electron mobility on the axial electric field E.

Figure 6.Dependences of diffusion coefficient on the axial electric field E.

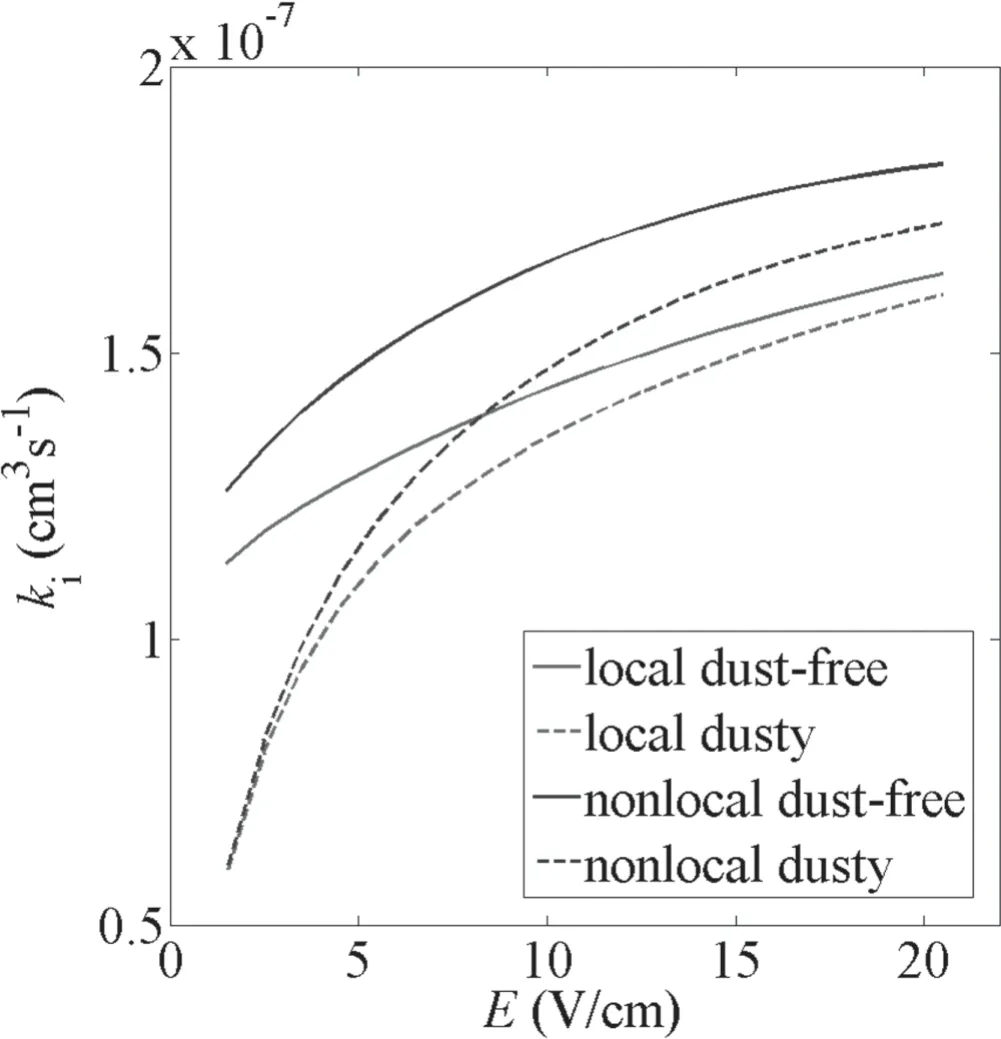
Figure 7.Dependences of ionization rate coefficient on the axial electric field E.

Figures 5 and 6 illustrate the dependences of electron mobility and diffusion coefficients on the axial electric field.It can be seen that,in dust-free plasmas,electron mobility does not change much with the increasing axial electric field and there is no significant difference between the local and nonlocal results.The electron diffusion coefficient decreases with the increasing axial electric field,because the electron collision frequency increases with the increasing axial electric field.When dust particles are introduced(nd=106cm?3),we find that the electron mobility calculated from the local and nonlocal kinetic models increases obviously at low axial electric field since the anisotropy of EEDFs is visibly enhanced by dust particles.Also,the effect of dust particles on nonlocal mobility is more obvious compared with the local case since the high energy electron(which can be collected by dust particles) proportion in nonlocal EEDFs is higher.With the increase of axial electric field,the mobility obtained from the local and nonlocal kinetic model decreases since the influence of dust particles on EEDF profiles becomes weaker.The diffusion coefficients calculated from the local and nonlocal kinetic model decrease when dust particles appear since the additional electron–dust collisions are introduced.

The ionization rate coefficients for dust-free and dusty plasmas are plotted as a function of axial electric field E in figure 7.With the increase of axial electric field,the ionization rate coefficients have a similar variation trend with electron effective temperature since both of them are positively proportional to electron energy.Dust particles can dramatically decrease the ionization rate coefficient at low axial electric field since the proportional of the high energy electrons collected by dust particle is relatively high at low axial electric field.Meanwhile,ionization rate coefficients calculated from the local and nonlocal kinetic model also have some difference to some extent due to the difference between the local and nonlocal EEDF profiles.

4.Conclusion

The local and nonlocal kinetic models are developed for analyzing the EEDF,electron transport and ionization rate coefficients of DC glow discharge dusty plasma.The influences of dust particles and the simplification method (local approximation or nonlocal approach)used for the Boltzmann equation on these plasma properties are calculated and discussed.The corresponding conclusions are presented as follows.

For both of dust-free and dusty plasmas,the EEDFs calculated based on the local and nonlocal kinetic models are different and all deviate significantly from the Maxwellian distribution.Dust particles reduce the population of high energy electrons and dramatically make the profiles of EEDFs shift to lower energy because of the collection of energetic electrons by dust particles.With the increase of axial electric field,the influence of dust particles on EEDFs becomes less noticeable.For dust-free plasma,the electron mobility calculated based on the local and nonlocal EEDFs does not differ much and changes slightly with the increasing axial electric field.The electron diffusion coefficient obtained from the nonlocal kinetic model is lower than that from the local model and both of them decrease with the increasing axial electric field.When dust particles are introduced(nd=106cm?3),the local and nonlocal electron mobility gets much higher at low axial electric fields and decreases with the increasing axial electric field.The effect of dust particles on nonlocal mobility is more obvious compared with the local case since the high energy electron proportion in nonlocal EEDFs is higher.Meanwhile,the diffusion coefficients calculated from the local and nonlocal kinetic model decrease when dust particles appear since additional electron–dust collisions are introduced.The ionization rate coefficients have a similar variation trend with electron effective temperature since both of them are positively proportional to electron energy.And the dust particles can dramatically decrease the ionization rate coefficient at low electric field.

Based on the calculation results in this paper,we reach a conclusion that the electron transport and ionization rate coefficients can be obviously affected by dust particles and the choice of simplification method for the Boltzmann equation.For simulating the gas discharge process with dust particles more accurately,the electron transport and ionization rate coefficients should be calculated with a proper kinetic model and dust particles should be considered too.

Acknowledgments

The research has been financially supported by National Natural Science Foundation of China (Nos.11775062 and 61601419),and the Key Laboratory Foundation of National Key Laboratory of Electromagnetic Environment (No.614240319010303).

ORCID iDs

Yonggan LIANG (梁勇敢)IANG (梁勇敢) https://orcid.org/0000-0002-9266-7499 https://orcid.org/0000-0002-9266-7499