CHEN Mengxi(陳夢茜）,WANG Zhiyong(王智勇)

( School of Mathematics and Satistics,Nanjing University of Information Science and Technology ,Nanjing 210044,China)

Abstract: This paper is dedicated to study the periodic solutions for a class of damped vibration problems.By virtue of auxiliary function,we obtain some kinds of new superquadratic growth and asymptotically quadratic growth conditions.Using the minimax methods in critical point theory,we establish some existence results,which unify and generalize some known results in the literature.

Key words: Minimax method; Asymptotically quadratic; Superquadratic; Periodic solution

1.Introduction and Main Results

Consider the damped vibration problem{

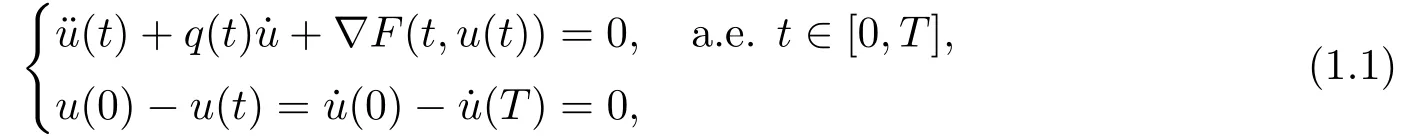
whereT >0,q ∈L1(0,T;R+),q(t)dt=0 andF:[0,T]×RN→R satisfies the following assumption:

(A)F(t,x)is measurable intfor everyx ∈RNand continuously differentiable inxfor a.e.t ∈[0,T],and there exista ∈C(R+,R+),b ∈L1(0,T;R+)such that

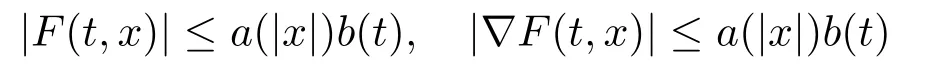
for allx ∈RNand a.e.t ∈[0,T].

Whenq(t)≡0,the problem (1.1)reduces to the following classical second order nonautonomous Hamiltonian system{

In the past few decades,considerable attention has been drawn to the existence of periodic solutions for the problem(1.2)under various conditions[1?5].In 2004,for superquadratic case,TAO and TANG[4]investigated the periodic solutions of the problem (1.2)and established the following result.

Theorem ASuppose thatFsatisfies assumption (A)and the following conditions:

(S1)F(t,x)≥0,?(t,x)∈[0,T]×RN;

(S2)uniformly for a.e.t ∈[0,T];

(S3)uniformly for a.e.t ∈[0,T];

(S4)uniformly for someM >0 and a.e.t ∈[0,T];

(S5)uniformiy for some?>0 and a.e.t ∈[0,T],

whereω=2π/T,r >2,μ>r?2 and (·,·),|·|are the Euclidean inner product and norm in RN.Then problem (1.2)has at least one non-constant periodic solution.

For the asymptotically quadratic case,applying generalized mountain pass theorem,MA and ZHANG[5]have proved that the problem (1.2)has at least one non-constant periodic solution.Concretely speaking,they obtained the following theorems.

Theorem BSuppose thatFsatisfies the assumption(A),the conditions(S1)-(S3)and the following conditions:

(S?4)uniformly for someM >0 and a.e.t ∈[0,T];

(S6)There existsγ ∈L1(0,T;R+)such that

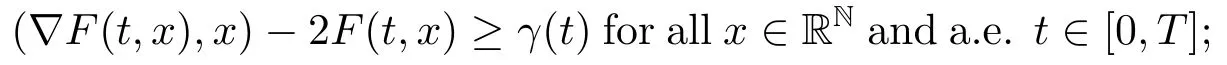
(S7)uniformly for a.e.t ∈[0,T].

Then the problem (1.2)has at least one non-constant periodic solution.

Theorem CSuppose thatFsatisfies the assumption (A),the conditions (S1)-(S3),(S?4)and the following conditions:

(S?6)There existsγ ∈L1(0,T;R+)such that

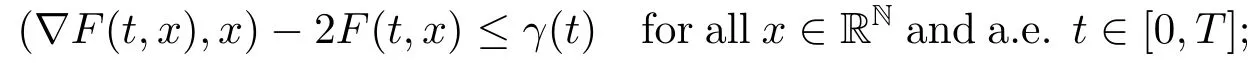
(S?7)uniformly for a.e.t ∈[0,T].

Then the problem (1.2)has at least one non-constant periodic solution.

In the present paper,motivated by[2,4-7],introducing some new kinds of superquadratic and asymptotically quadratic conditions,we develop some new analytic techniques to prove that the problem (1.1)admits a non-constant periodic solution.We stress that our results are all new even without damped vibration term.For the sake of convenience,we set

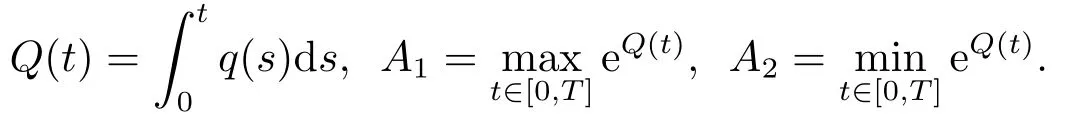
Now,we can state our main results.

Theorem 1.1Suppose thatFsatisfies the assumption(A)and the following conditions:

(F1)?x ∈RN;

(F2)uniformly for a.e.t ∈[0,T];

(F3)uniformly for a.e.t ∈[0,T];

(F4)There existh(s)∈C(R+,R+)andM >0 such thatuniformly for a.e.t ∈[0,T];

(F5)There existM1>0 andσ(s)∈C(R+,R+)withis nondecreasing ins ∈R+,whereh(s)is defined in (F4),such that eQ(t)[(?F(t,x),x)?2F(t,x)]≥σ(|x|),?|x|≥M1and for a.e.t ∈[0,T].Then the problem (1.1)has at least one non-constant periodic solution.

Remark 1.1Conditions (F1)-(F3)were due to [7].From [7],we know that (S1),(S4)and (S5)could implyμ ≤r.We claim that (S4)and (S5)are special cases of (F4)and (F5)when (S1)holds.In fact,we only need to takeh(s)=sr,σ(s)=?sμandM1large enough,where?>0,r >2,μ>r?2.We can check thatFurthermore,is non-decreasing insfor alls ∈R+byμ≤r.Therefore,h(s)andσ(s)satisfy all conditions of(F4)and(F5).From the discussions above,we see that Theorem 1.1 significantly extends and improves Theorem A.

Remark 1.2Theorem 1.1,the main result of [7],has introduced the following new non-quadratic conditions:

(F?4)uniformly for someM >0 and a.e.t ∈[0,T];

(F?5)there existM1>0,μ > r?2 andk1∈C(R+,R+)withandk1(s)is non-increasing insfor alls ∈R+,such that eQ(t)[(?F(t,x),x)?2F(t,x)]≥k1(|x|)|x|μ,?x ∈RN,|x|≥M1and for a.e.t ∈[0,T].Here,ifμ≤r,we emphasize that these new non-quadratic conditions (F?4)and (F?5)are also special cases of assumptions (F4)and (F5).Indeed,seth(s)=sr,σ(s)=k1(s)sμ.Using the properties ofk1(s),a direct computation shows thatmoreover,we haveis non-decreasing insfor alls ∈R+since1,?s ≤tbyμ≤r.Therefore,in some sense,Theorem 1.1 also generalizes Theorem 1.1 of [7]whenμ≤rholds.

Remark 1.3There are functionsF(t,x)satisfying the assumptions of Theorem 1.1 and not satisfying Theorem A and the mentioned results above.For example,letq(t)≡0,and consider Noticethen the results of[6]cannot be applied.By simply computation,for anyμ>0,one has

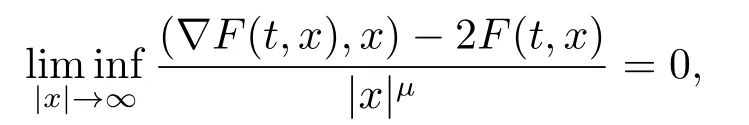
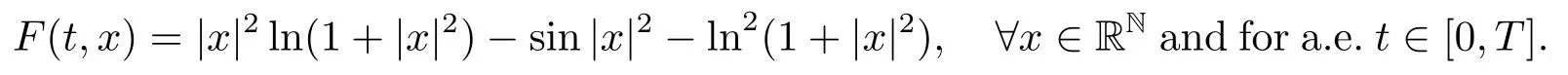
which implies that functionF(t,x)does not satisfy the assumption (S5).Hence,Theorem A,Theorem 1.2 in [2]and Theorem 1 in [4]cannot be applied too.At the same time,we can find that the result of Theorem 1.1 in [7]also does not satisfy the properties ofk1(s).Nevertheless,leth(s)=s2ln(1+s2),σ(s)=ln2(1+s2),and it is not difficult to see that all conditions of Theorem 1.1 are satisfied.So,by Theorem 1.1,the problem (1.1)has at least one non-constant periodic solution.

Corollary 1.1Suppose thatFsatisfies the assumptions(A),(F1)-(F3)and the following conditions:

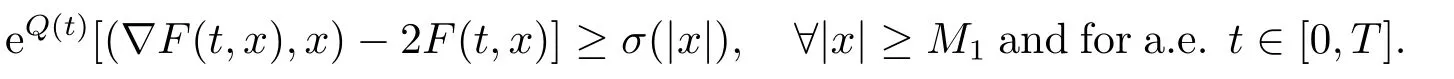
Then the problem (1.1)has at least one non-constant periodic solution.

Remark 1.4Corollary 1.1 seems like a new result.In contrast to Theorem B,Corollary 1.1 removes the assumption (S6)completely although it uses a few stronger conditioninstead of (S7).

Corollary 1.2Suppose thatFsatisfies the assumptions (A),(F1)-(F3),(F??4)and the following condition:

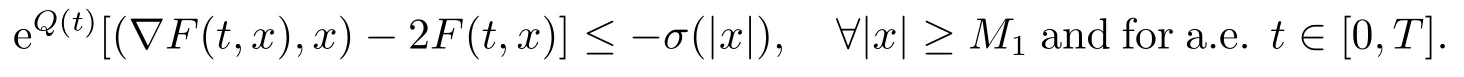
Then the problem (1.1)has at least one non-constant periodic solution.

The rest of this paper is arranged as follows.In Section 2,some necessary notations and preliminaries are introduced.In Section 3,we prove the energy functional associated with the problem (1.1)satisfies the (C)condition (see Definition 2.2 below),then we can adopt the same arguments of [7]to prove our main results by the generalized mountain pass theorem in[1].

2.Preliminaries

LetH1T:= {u:[0,T]→RN| uis absolutely continous,u(0)=u(T),∈L2(0,T;RN)} be a Hilbert space with the inner product

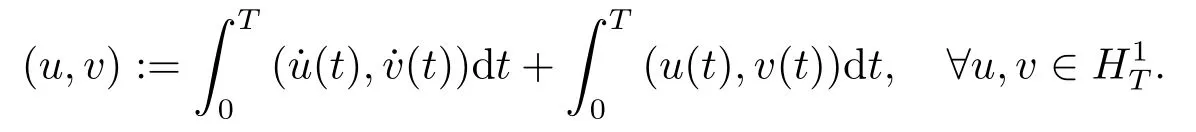
The corresponding norm is

where

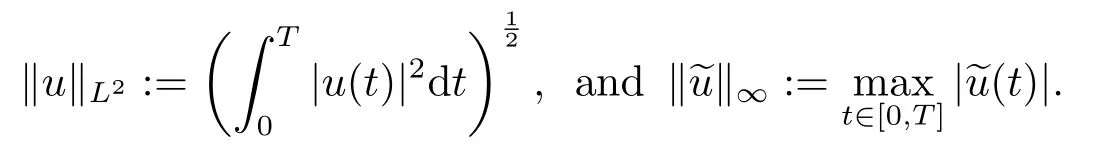
Since the embedding ofH1TintoC(0,T;RN)is compact,there existsd>0 such that

for allu ∈H1T.

It follows from the assumption (A)that the functionalφonH1Tgiven by

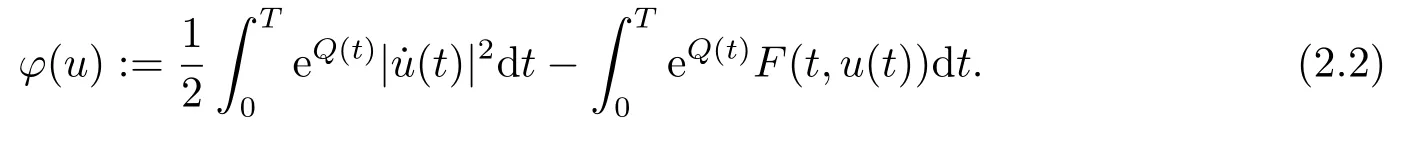
Thenφis continuously differentiable onH1T(see [1]).Moreover,

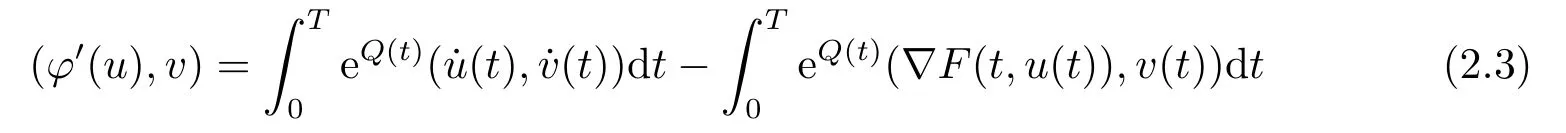
for allu,v ∈H1T.It is well known that the periodic solutions to the problem(1.1)correspond to the critical points ofφ(see [1]).

Definition 2.1[1]LetEbe a real Banach space.We say that{un} inEis a Palais-Smale sequence ((PS)sequence)forφifφ(un)is bounded andφ′(un)→0 asn→+∞.The functionalφ ∈C1(E,R)satisfies the Palais-Smale condition ((PS)condition)if any Palais-Smale sequence contains a convergent subsequence.

Definition 2.2[8]LetEbe a real Banach space.We say that{un} inEis a Cerami sequence ((C)sequence)forφifφ(un)is bounded andφ′(un)(1+||un||)→0 asn→+∞.Then functionφ ∈C1(E,R)satisfies the Cerami condition ((C)condition)if any Cerami sequence contains a convergent subsequence.

Lemma 2.1[1](Generalized mountain pass theorem)LetEbe a real Banach space withE=V ⊕X,whereVis finite dimensional.Supposeφ ∈C1(E,R)satisfies the(PS)condition,and

(i)There existρ,α >0 such thatφ|?Bρ∩X ≥α,whereBρ:={u ∈E| ||u||≤ρ},?Bρdenotes the boundary ofBρ;

(ii)There existe ∈?B1∩Xands0>ρsuch that ifthenφ|?Q ≤0.

Thenφpossesses a critical valuec ≥αwhich can be characterized as

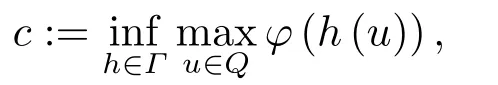
whereΓ:= {h ∈C(,E)|h=id on?Q},here,id denotes the identity operator.

Remark 2.1As we can see in [9],a deformation lemma can be proved with the weaker(C)condition replacing the usual (PS)condition,and it turns out that Lemma 2.1 holds true under the (C)condition.

3.Proofs of Main Results

In the following,we denote various positive constants asCi,i=1,2,3,···.

Lemma 3.1Assume that ( A),(F3)-(F5)hold,then the functionalφsatisfies the (C)condition.

ProofLetE:=H1T,suppose that{un}?H1Tis a (C)sequence ofφ,then there existsC1>0 such that

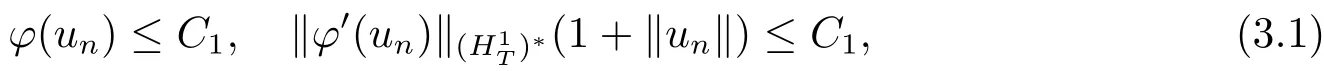
where (H1T)?is the dual space ofH1T.

To begin with,by (F4),there existsM2>0 such that eQ(t)F(t,x)≤Mh(|x|),for all|x|≥M2and a.e.t ∈[0,T],which jointly with the assumption (A)that

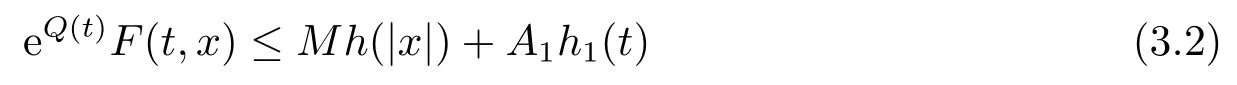
for allx ∈RNand a.e.t ∈[0,T],whereh1(t):=max|x|≤M2a(|x|)b(t)≥0.It follows from(2.2),(2.3),(3.1)and (3.2)that

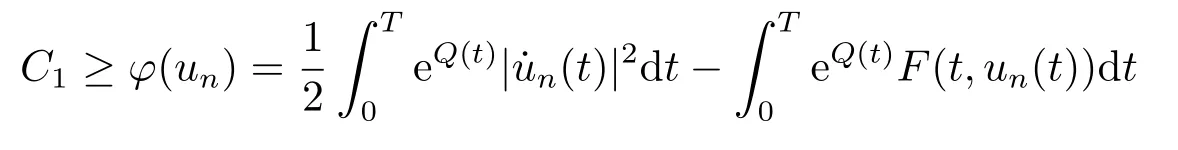
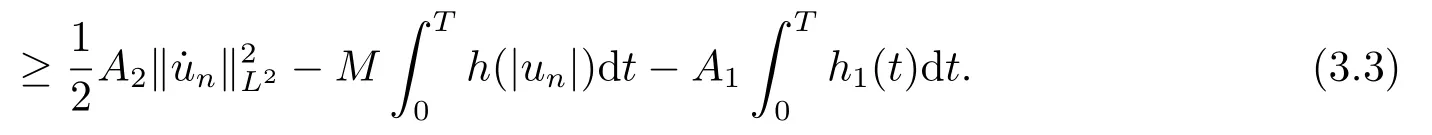
On the other hand,(F5)and the assumption (A)yield

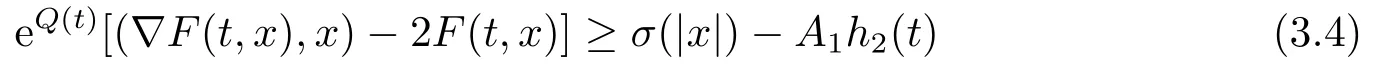
for allx ∈RNand a.e.t ∈[0,T],whereh2(t):=(2+M1)max|x|≤M1a(|x|)b(t)≥0.It follows from (2.2),(2.3),(3.1)and (3.4)that

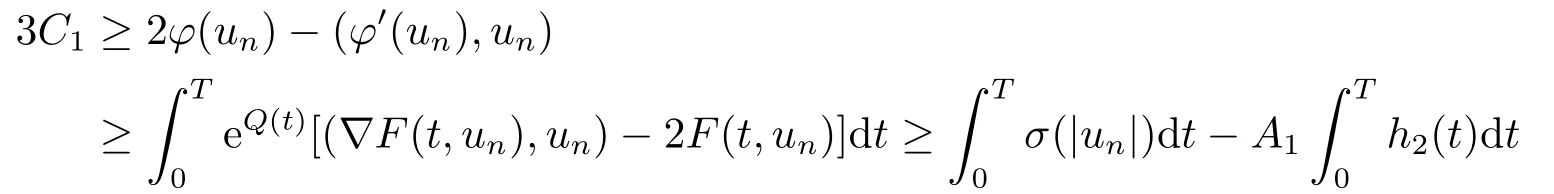
for alln ∈N.Hence,we have

for alln ∈N.From (3.3),(3.5)and the property ofh(s)/σ(s),one has

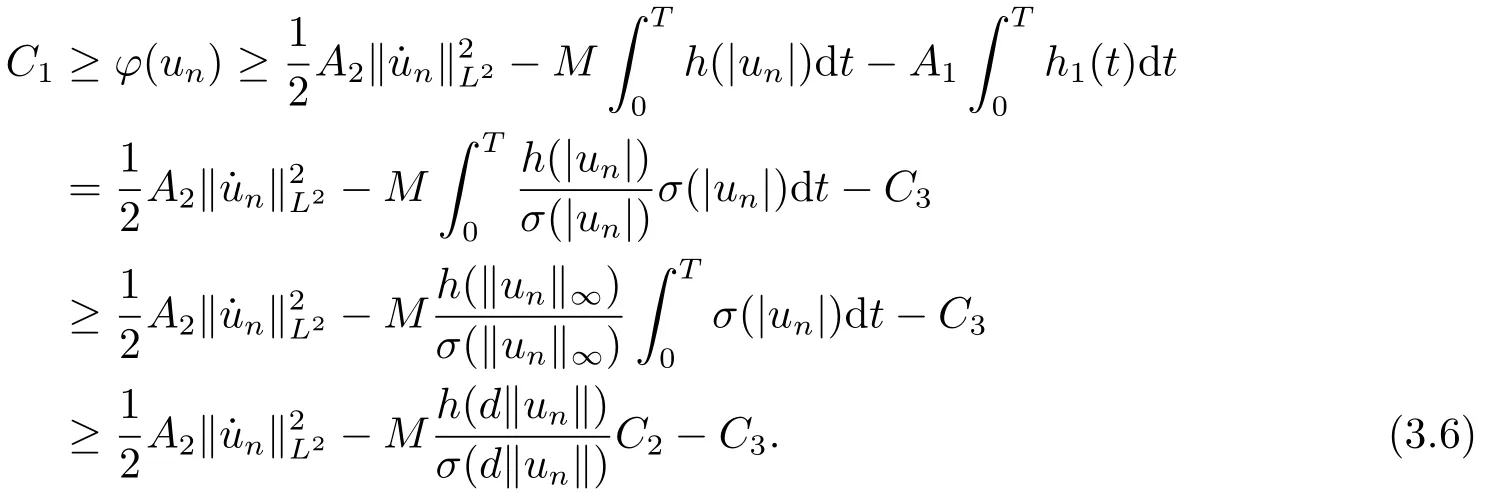
Finally,we claim that{un} is bounded.If{un} is unbounded,we may assume,without loss of generality,that||un||→+∞asn→+∞.Putvn:=thenvnis bounded inHT1.

Hence,there exists a subsequence,again denoted byvn,such that

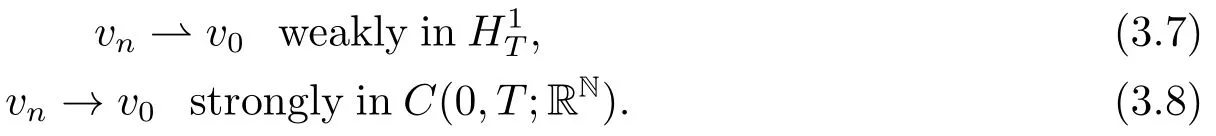
Diving both sides of (3.6)by||un||2,using the property ofwe can find that

Hence,it follows from (3.8)and (3.9)thatvn→asn→+∞,which implies thatv0=andT||2=||||2=1.

Consequently,

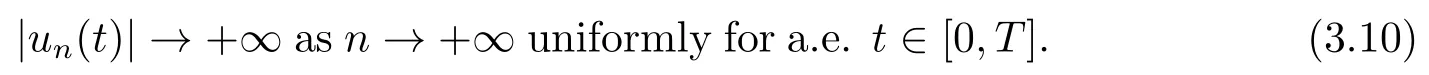
What’s more,it follows from (F3)that there existsM3>0 such that

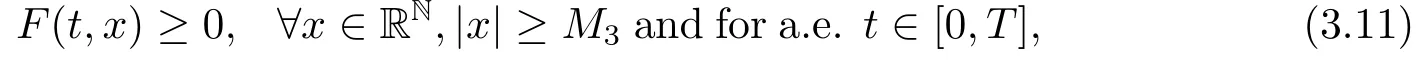
which implies thatF(t,x)≥?h3(t),?x ∈RNand for a.e.t ∈[0,T],by the assumption (A),whereh3(t):=max|x|≤M3a(|x|)b(t)≥0.Denote?n:={t ∈[0,T]||un(t)|≥M3}.By (3.10),we have meas (?n)>0.So,from (F3),(3.10),(3.11)and Fatou’s Lemma,we get

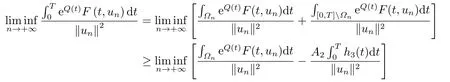
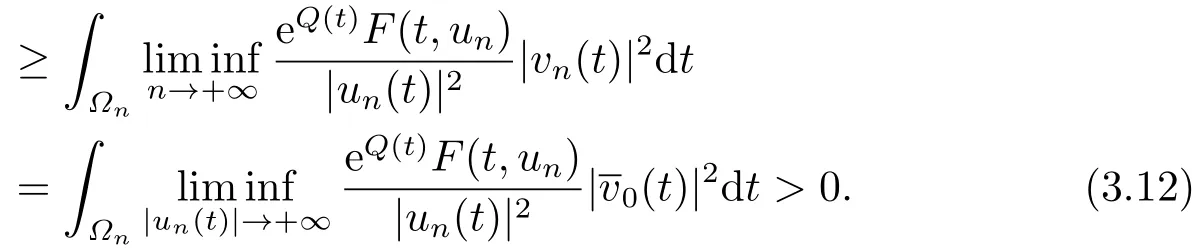
However,by (3.1)and (3.9),we have

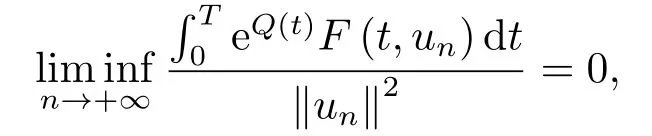
which contradicts (3.12).Thus,{un} is bounded inH1T.Using the same arguments as in [4],we could get{un} possesses a strong convergent subsequence.Therefore,φsatisfies the (C)condition.

Next,we only give the proofs of Theorem 1.1.Corollary 1.1.Corollary 1.2 can be proved similarly.

Proof of Theorem 1.1By Lemma 3.1,we know thatφsatisfies the (C)condition.Using the same arguments as used in [7],we see that assumptions (i)and (ii)of Lemma 2.1 are all satisfied.Then,from Lemma 2.1,the problem (1.1)has at least one non-constant periodic solution inH1T.

Proof of Corollary 1.1Clearly,takingh(s)=s2,by Theorem 1.1,we can obtain that the problem (1.1)has at least one non-constant periodic solution inH1Timmediately.