Parameterized Post-Post-Newtonian Light Propagation in the Field of One Spherically-Symmetric Body?
Xiao-Yan Zhu (朱小彥), Bo Yang (楊波), Chun-Hua Jiang (江春華), and Wen-Bin Lin (林文斌),
1School of Mathematics and Physics,University of South China,Hengyang 421001,China
2School of Physical Science and Technology,Southwest Jiaotong University,Chengdu 610031,China
Abstract We derive a more generally parameterized post-post-Newtonian solution for the light propagation in the gravitational field of one spherically-symmetric body.Based on the solution for the light velocity,we give the formula of the light deflection when both the emitter and receiver are located in the regions far away from the body,which is the most important scenario in the real applications.Our results can be applied to more metric theories of gravitation.
Key words: PPN,spherically-symmetric metric,light propagation,light deflection
1 Introduction
The light propagation in the gravitational field serves key tests for the theories of gravitation.The light deflection,time delay and gravitational redshift are the fundamental predictions of general relativity (GR) and have been found in good agreement to the first post-Newtonian (PN) order with the observations.[1]With the development of technologies and the demands of the future observations,the higher PN effects on the light propagation have also been explored extensively,e.g.,the light deflection,[2?15]the time delay,[16?18]and the gravitational redshift.[19,20]At the same time,since the parametrized post-Newtonian (PPN) formalism[21,22]can characterize the weak-field-limit metric of a broad spectrum of gravitation theories,thus it has been employed in making the theoretical predictions for the light propagation.[2?5,7?9,16,23?28]
Similar to Klioner and Kopeikin’s work on the motion of binary compact systems under a more generally parameterized 2PN acceleration,[29]in this work we derive the 2PN solution for the light propagation in a more generally PPN framework for the external field of the sphericallysymmetric body.Compared to the conventional PPN models,this work includes more parameters,which makes the formulation of the light propagation be applicable to more gravitation theories at the 2PN order.Specifically,the combinations of these parameters may describe not only the weak-field-limit metrics of the Brans-Dicke theory(BDT)and the scalar-tensor theories discussed in Refs[25,30,31],but also those of the non-minimal Einstein-Yang-Mills theory and wormholes spacetime,[32?37]as well as the interaction between gravitational and electromagnetic fields beyond the Einstein-Maxwell theory.[38,39]Based on the solution of the light velocity,we further give the formula for the 2PN deflection of light for an interesting scenario in the astronomical applications,in which both the light emitter and receiver are located in the regions very far away from the body.
2 The Second-Order PPN Metric and Geodesic Equation for the Field of the Spherically-Symmetric Body
We consider the second-order PPN metric for the field of the spherically-symmetric body as follows,
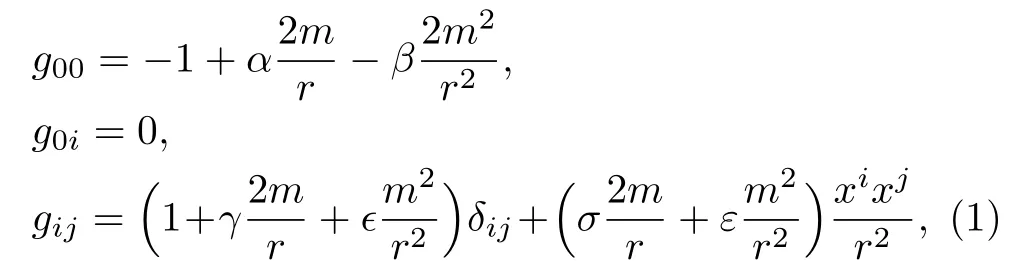
where the metric has signature of (?+++),andmdenotes the mass of body.The gravitational constant and the light speed in vacuum have been set as 1.Latin indicesiandjrun from 1 to 3.denotes the distance from the field position(x1,x2,x3)to the body located at the coordinate origin.The PPN framework are characterized by the parametersα,β,γ,σ,?andε.The parameterαis usually absorbed into the definition of the gravitational constant,while we keep it here for the completeness of a general second-order PPN metric,as Ref.[29] did for the general PPN acceleration.β,γand?are the conventional PPN parameters.[16]The parameterεis introduced in Ref.[27] to include more gravitational theories.The discussions of the physical motivation for this parameter can be found in Refs.[25,27] so we do not repeat them here.The parameterσis newly introduced in this work.Table 1 lists some representative PPN frameworks of the static spherically-symmetric body’s field for light propagation.The relations between the parameters in these references and ours are also shown for readers’convenience.
The values of?andεfor some scalar-tensor theories and the Einstein-aether theory in the harmonic coordinates have been tabulated in Ref.[27].Table 2 gives the values ofβ,γ,σfor GR and BDT in the harmonic coordinates.Hereωis a dimensionless constant of BDT,and when it’s value goes to infinity BDT will reduce to GR.
The dynamics equation of the test particles including the photon for the metric form given by Eq.(1) can be written as
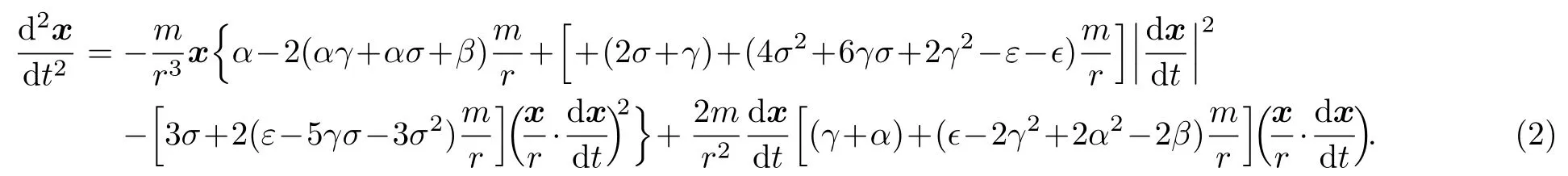
For the photon’s motion,it also satisfies the null-geodesic condition,which in the 2PN approximation reads


Table1 Comparisons of some representative PPN frameworks of the spherically-symmetric body’s field for light propagation.

Table2 The values ofβ,γ,σ for GR and BDT withω being a dimensionless constant in the harmonic coordinates.[40]
From this equation we can obtain the photon’s velocity when the position and velocity direction of the photon are given.This equation can be employed to simplify the derivation of the light propagation when solving the dynamics equation.
3 The 2PN Solution for the Light Propagation
In this section we employ an iterative method[1,41,42]to derive the 2PN solution for the light propagation in the spacetime characterized by the above PPN metric.
We assume there is a photon emitted at the coordinate timeteat the positionxewith an initial velocity direction described by the unit vectorn.
For the zeroth-order order (Minkowskian spacetime),Eqs.(2) and (3) reduce to

and the corresponding solutions (Newtonian solution) are

wherexNdenote the Newtonian trajectory.
Before we present the PN solutions,we introduce an important parameter for the light deflection in the gravitational field — the impact vectorb,which joins the body’s center and the point of the closest approach in the line ofxN,and whose amplitudeis well-known as the impact parameter.[40,41]
To the 1PN accuracy,Eqs.(2) and (3) reduce to

and the corresponding solutions can be written as the following form

withx1PNbeing the first-order post-Newtonian term.
Substituting Eqs.(6) and (9) into Eqs.(7) and (8),and only keeping the 1PN terms,we can obtain
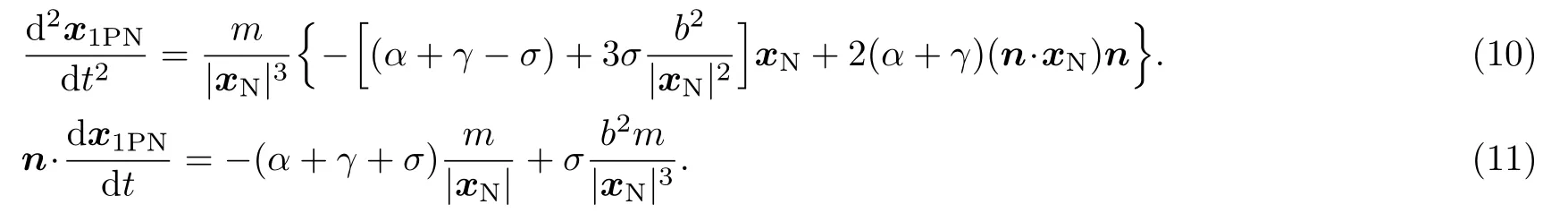
We decomposex1PNinto the components being parallel and perpendicular ton:

Eqs.(10)?(11) then yield

Integrating Eq.(14),we can get

Combining Eqs.(15) and (16),we have the velocity of the particle to the 1PN accuracy

Integrating Eq.(17),we can obtain the 1PN contributions to the photon’s trajectory as follows,

To the 2PN accuracy,the solution of Eqs.(2) and (3) can be written as

withx2PNbeing the 2PN correction.
Substituting Eq.(19) into Eq.(2),making use of Eqs.(6),(10),(17),(18),we can obtain

Similarly,we can decomposex2PNinto the components being parallel and perpendicular ton:

Integrating Eq.(20) for the components being perpendicular ton,we can obtain

Substituting Eqs.(19) and (22) into Eq.(3),and making use of Eqs.(6),(17) and (18),we can obtain

Finally,the 2PN correction to the trajectoryx2PNcan be achieved via integrating Eqs.(23)?(24) as follows

The photon’s trajectory in the 2PN approximation is described by the combinations of Eqs.(19) with (6),(18)and (25).The corresponding velocity is described by the summation of Eqs.(5),(17),(23) and (24).
Most integrals used in this section can be found in our previous work,[41]and the other integrals are listed in Appendix for readers’ convenience.
4 The 2PN Light Deflection in the Field of a Spherically-Symmetric Body
In real applications,people are usually interested in the gravitational deflection of light when the emitter and receiver are both far away from the body.In this case,we only need the light velocity at the locations of the emitter and the receiver whose distances from the body can be approximated as infinity.In this case,from Eqs.(5),(17),(23) and (24),we can write the light velocity at the emitter and the receiver as follows:

Therefore,the parameterized second-order PN light deflection in the field of a spherically-symmetric body can be formulated as

It can be easily checked that the 2PN light deflection for the Schwarzschild black hole in GR isOur result is also consistent with the 2PN light deflection in the scalar-tensor theory given in Ref.[31].
5 Summary
In this work,we have derived the light propagation under a generally parameterized second-order post-Newtonian framework for the gravitational field of the spherically-symmetric body.Especially,we include more parameters in the PPN frame,which enables the formulations be applicable to more metric theories,as well as in different coordinates.With the development of the observational technologies,the achieved parameterized 2PN light-deflection formula may be useful in the discriminations of different gravitational theories in future.
Appendix: Lists of Integrals
Most integrals used in the above derivations have been given in Ref.[41].Here we give some new integrals for readers’ convenience.

Acknowledgement
The authors would like to thank the reviewer for her/his constructive suggestions on promoting the quality of this work.
 Communications in Theoretical Physics2019年12期
Communications in Theoretical Physics2019年12期
- Communications in Theoretical Physics的其它文章
- Magnetohydrodynamic Stagnation Point Flow of a Maxwell Nanofluid with Variable Conductivity
- An Optimal Analysis for 3D Flow of Prandtl Nanofluid with Convectively Heated Surface
- The Effects of Wettability on Primary Vortex and Secondary Flow in Three-Dimensional Rotating Fluid?
- An Improved Heterogeneous Mean-Field Theory for the Ising Model on Complex Networks?
- Relativistic Self-Focusing of Hermite-cosh-Gaussian Laser Beam in Magnetoplasma with Exponential Plasma Density Ramp
- Periodic Orbits Around Kerr Sen Black Holes?
