Mei-Xia Chu (褚美俠),Bo Tian (田播), Yu-Qiang Yuan (袁玉強(qiáng)),Ze Zhang (張澤),and He-Yuan Tian (田賀元)

State Key Laboratory of Information Photonics and Optical Communications,and School of Science,Beijing University of Posts and Telecommunications,Beijing 100876,China

Abstract Twin-core optical fibers are applied in such fields as the optical sensing and optical communication,and propagation of the pulses,Gauss beams and laser beams in the non-Kerr media is reported.Studied in this paper are the coupled cubic-quintic nonlinear Schr?dinger equations with variable coefficients,which describe the effects of quintic nonlinearity for the ultrashort optical pulse propagation in a twin-core optical fiber or non-Kerr medium.Based on the integrable conditions,bilinear forms are derived,and dark-dark soliton solutions can be constructed in terms of the Gramian via the Kadomtsev-Petviashvili hierarchy reduction.Propagation and interaction of the dark-dark solitons are presented and discussed through the graphic analysis.With different values of the delayed nonlinear response effect b(z),where z represents direction of the propagation,the linear- and parabolic-shaped one dark-dark soltions can be derived.Interactions between the parabolic- and periodic-shaped two dark-dark solitons are presented with b(z)as the linear and periodic functions,respectively.Directions of velocities of the two dark-dark solitons vary with z and the amplitudes of the solitons remain unchanged can be observed.Interactions between the two dark-dark solitons of different types are displayed,and we observe that the velocity of one soliton is zero and direction of the velocity of the other soliton vary with z.We find that those interactions are elastic.

Key words: optical fiber,coupled cubic-quintic nonlinear Schr?dinger equations,dark-dark solitons,Kadomtsev-Petviashvili hierarchy reduction

1 Introduction

Twin-core optical fibers have been applied in such fields as the optical sensing[1]and optical communication,[2]which have embodied in the optical fiber sensors,[1]optical interferometers[2]and optical switches.[3]Propagation of the pulses,[4]Gauss beams[5]and laser beams[6?8]in the non-Kerr media has attracted the researchers’ attention.

Applications of the nonlinear Schr?dinger (NLS)-type equations in nonlinear optics,[6,9?10]plasma physics,[11?13]hydrodynamics[14?15]and Bose-Einstein condensation[11,16]have attracted the researchers’ attention.In nonlinear optical fibers,optical solitons,which are produced by the balance between the nonlinear effect and group velocity dispersion,have been described by the NLS-type equations.[6,17?20]With the consideration of the two solitons simultaneously propagate in the two-mode fiber or birefringent,the coupled NLS equations have been investigated.[21?24]

When the intensity of the incident light field becomes stronger and non-Kerr nonlinearity plays a role,the NLStype equations with higher-order nonlinearity terms have been used for describing the pulses in optical fibers.[25?29]Combination of the cubic and quintic nonlinearity terms has allowed stable multidimensional structure exist of the cubic-quintic NLS equation.[30?31]So as to describe the effects of quintic nonlinearity for the ultrashort optical pulse propagation in a twin-core optical fiber or non-Kerr medium,people have studied the following coupled cubicquintic NLS equations with variable coefficients,[32?35]

whereq1andq2represent the two components of the electromagnetic fields,the subscriptszandtdenote the partial derivatives with respect to the scaled distance along the direction of the propagation and retarded time,respectively,“?” represents the complex conjugate,k(z) andm(z) depict the group velocity dispersions,φ(z)andπ(z) denote the nonlinearity parameters,?(z) andω(z) are the saturations of the nonlinear refractive indexes,l(z) andn(z) represent the self-steepening effects,h(z) andb(z) are the delayed nonlinear response effects.To our knowledge,the conservation laws,Lax pair,Darboux transformation (DT),[32]rogue wave solutions,[33]mixed-type vector solitons,[34]bright and dark solitons and B?cklund transformations[35]for Eqs.(1) have been studied.Refs.[32,35] have presented the integrable conditions for Eqs.(1),which can be rewritten as

whereRandvare the real constants.Special cases of Eqs.(1) have been given as

(i) Whenk(z) =m(z) = 1,φ(z) =π(z) = 2,?(z) =ω(z) =ρ21,l(z) =n(z) =h(z) =b(z) = 2ρ1,Eqs.(1) have been reduced to the coupled cubic-quintic NLS equations,[36]

Soliton solutions and DT for this case have been investigateded.[36]

(ii) Whenq1=qandq2= 0,Eqs.(1) have been reduced to the variable coefficients Kundu-Eckhaus equation,[37]

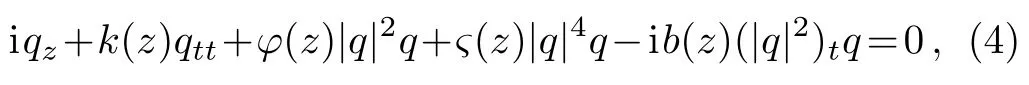
which depicts the ultra-short femtosecond pulses propagate in optical fibers,whereq(z,t)are the electromagnetic wave,b(z)is the nonlinear dispersion.Soliton interactions for this case have been studied via the Hirota method.[37]

However,dark-dark soliton solutions for Eqs.(1) have not been studied.In Sec.2 of this paper,under Integrable Conditions (2),bilinear forms will be constructed,and dark-dark soliton solutions for Eqs.(1) will be derived through the Kadomtsev-Petviashvili(KP)hierarchy reduction.In Sec.3,we will graphically analyze the interaction and propagation of dark solitons.Conclusions will be written in Sec.4.

2 Bilinear Forms and Dark Soliton Solutions for Eqs.(1)

In this section,we will consider the following variable transformations,

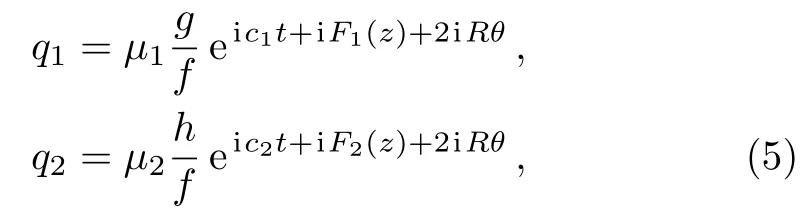
where

Now the fame of these wonders was noised abroad, and the people flocked in great numbers to see the three marvels24, and the maiden22 who had won them; and among the sightseers came the king s son, who would not go till everything was shown him, and till he had heard how it had all happened

gandhrepresent the complex functions ofzandt,fdenotes a real function,cj’s andμj’s are the real and complex constants,respectively.Substituting Variable Transformations (5) into Eqs.(1),we can derive the bilinear forms for Eqs.(1) with Integrable Conditions (2) as

where the Hirota bilinear operatorsDz,Dtare defined as[38]

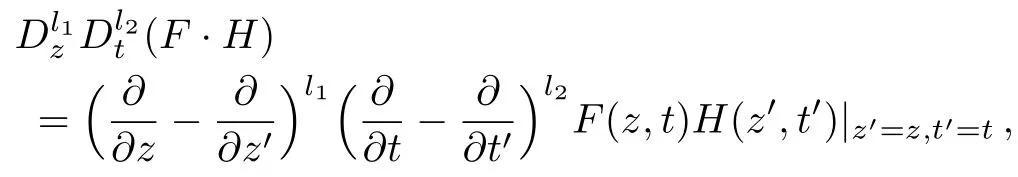
F(z,t) denotes an analytic function ofzandt,H(z′,t′)represents an analytic function of the formal variablesz′andt′,l1andl2are the non-negative integers.

Via Integrable Conditions (2),dark-dark soliton solutions in terms of the Gramian for Eqs.(1) can be constructed as

where

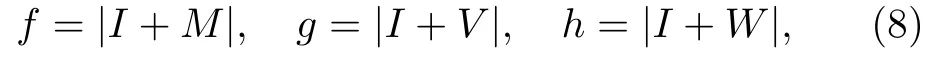
Irepresents theN × Nidentity matrix,Nis an nonnegative integer,M,VandWare theN×Nmatrices,of which elements aremkl,vklandwkl,respectively,defined as

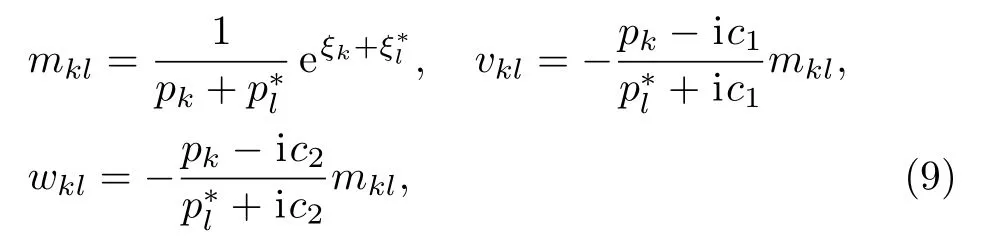
It is worth noting that the proof of the above process is similar to that in Ref.[39].It is observed thatvshould be negative according to Constraint (10).

WhenN= 1,one dark-dark soliton solutions via Solutions (7) can be derived as

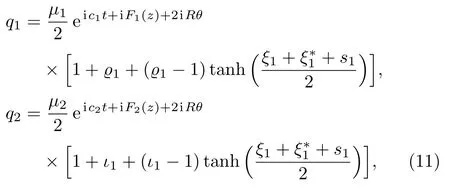
where

v,c1,c2,μ1,μ2,andp1satisfy

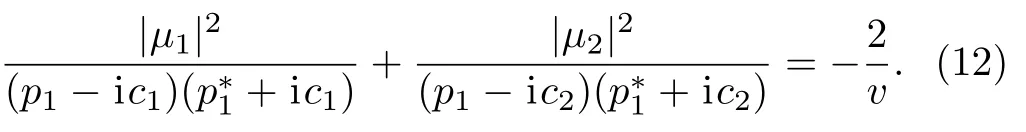
Based on Solutions (11),we require thats1>0,i.e.,p1+p?1>0,to guarantee Solutions (11) against the singularity.

WhenN=2,two dark-dark solutions via Solutions(7)can be presented as

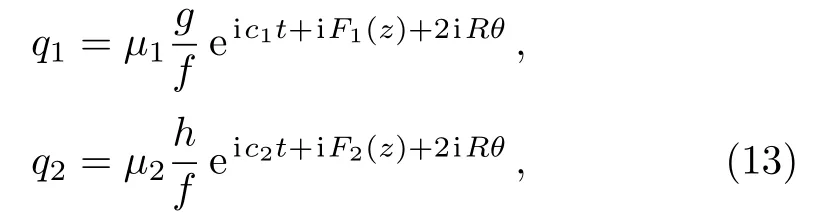
where

v,c1,c2,μ1,μ2,p1,andp2satisfy Constraint (10).Similarly,we require thats1>0 ands2>0,i.e.,p1+p?1>0 andp2+p?2>0,to guarantee Solutions (11) against the singularity.

3 Discussions

Based on Solutions (11) and (13),dark-dark solitons for Eqs.(1) will be displayed graphically.Via Solutions (11),amplitudeAkand velocityofq1andq2can be given as

which is the magnitude of

Direction ofWhen?(i/4R)(p1?p?1)b(z)>0,the soliton propagates along the positive direction oftaxis;When?(i/4R)(p1?p?1)b(z)<0,the soliton propagates along the negative direction oftaxis.We can see that the amplitude is irrelevant tob(z),the velocity ofqkis relevant tob(z).When (p1?ick)/(p?1+ick) = 1,amplitude ofqkreaches the maximum,and minimum intensity drops to zero at the same time.Theqkcomponent is black withp1?p?1=2ick,or else it is grey.

Hereafter we mainly discuss the case ofc12for Eqs.(1).Based on Solutions (11),q1=χq2(whereχis a constant) whenc1=c2,and the soliton is black in both theq1andq2components; whenc12,q12.More on the solitonic issues can be seen,e.g.,in Refs.[40].

In Fig.1,we choosec12,theq2component is black whenp1?p?1=2ic2.When the variable coefficientb(z)is a constant,velocity of the one dark-dark soliton remains unchanged when the soliton propagates,as shown in Fig.1.Whenb(z) = 2z,Fig.2 depicts the parabolicshaped dark-dark soliton,of which the direction of the velocity changes withz.

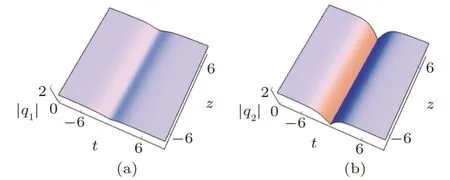
Fig.1 (Color online) Linear-shaped dark-dark soliton via Solutions(11)with the parameters asp1 =1/2+i/2,c1 = 0,c2 = 1/2,μ1 = 1,μ2 = 3/2,v =?2/11,R = 1,ξ1(0 )=0 andb(z)=1/7.

Fig.2 (Color online) Parabolic-shaped dark-dark soliton via Solutions(11)with the same parameters as those in Fig.1 except thatb(z)=2z.

When Im(p1)Im(p2)<0,Figs.3–4 show the head-on interactions between the two solitons of the same type with Im(pk) being the imaginary part ofpk.The solitonS1is black andS2is grey in theq1component whenp1?p?1= 2ic1,and just the opposite,in theq2component.Whenb(z) = 8/5+z,Fig.3 depicts interaction of the parabolic-shaped two dark-dark solitons,of which the directions of the velocities vary withz.The amplitudes in both theq1andq2components remain unchanged during the propagation.Whenb(z) = 5/2+(5/2)sin[(11/10)z],interaction of the periodic-shaped two dark-dark solitons is displayed in Fig.4.Amplitudes of the two solitons keep invariant during those interactions except that some phase shifts vary,implying that those interactions are elastic.

Fig.3 (Color online) Head-on interaction between the parabolic-shaped dark-dark solitons via Solutions (13),withp1 = 1+ i/2,p2 = 1?i/2,c1 = 1/2,c2 =?1/2,and b(z)=3+2z.

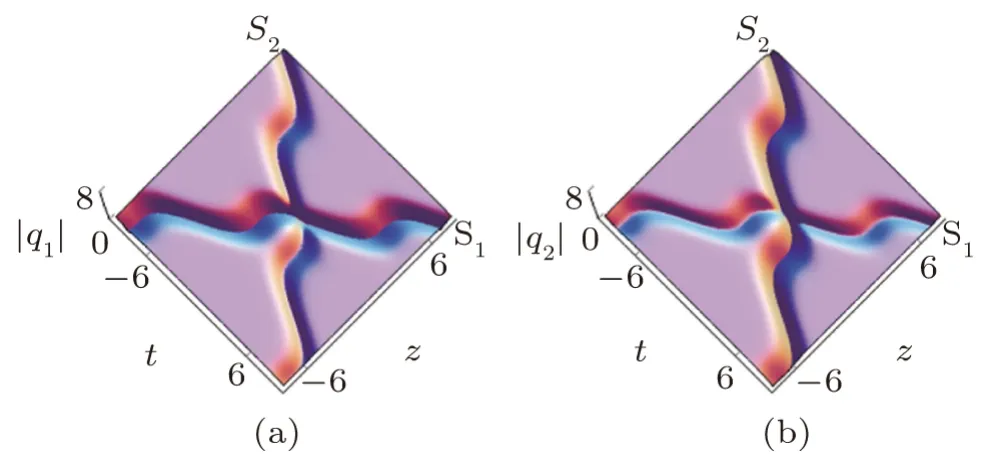
Fig.4 (Color online) Head-on interaction between the periodic-shaped dark-dark solitons via Solutions(13)with the same parameters as those in Fig.3 except thatb(z)=5/2+5/2 sin[(11/10)z].

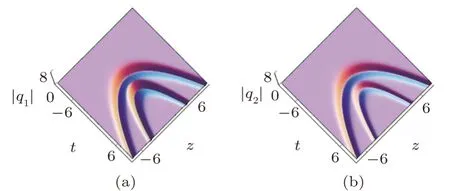
Fig.5 (Color online) Overtaking interaction between the parabolic-shaped two dark-dark soltions via Solu-tions(13),withp1 =1+i/3,p2 =1+i,c1 =1,c2 =?1,=0,andb(z)=1/7+(7/10)z.

When the two dark-dark solitons have the same velocity,which means that Im(p1) = Im(p2),we derive the bound-state dark-dark solitons based on solutions (13).Since the coefficients of the same nonlinear terms for Eqs.(1) are the same,similar to the analysis in Ref.[41],we cannot obtain the bound-state dark-dark solitons.When Im(p1)Im(p2)>0,Figs.5–6 illustrate the overtaking interactions of the two solitons with the same type.In Fig.5,parabolic-shaped two dark-dark solitons are displayed.Directions of the velocities of the two solitons change withzsimultaneously.Fig.6 displays the periodicshaped two dark-dark solitons,of which the directions of the velocities vary periodically.As we can see,the amplitudes of the above two dark-dark solitons are unaffected by those interactions,namely,those interactions are elastic.

Fig.6 (Color online) Overtaking interaction between the periodic-shaped two dark-dark soltions via Solutions (13) with the same parameters as those in Fig.5 except thatb(z)=1+sin(z/2).

Figures 7–8 show the interactions between the two solitons of different types when Im(q1)=0.Velocities of the linear-shaped dark soliton are zero.Fig.7 illustrates the interaction between the linear-shaped dark solitonS1and parabolic-shaped dark solitonS2.Interaction between the linear-shaped dark soliton and periodic-shaped dark soliton is displayed in Fig.8.Similar to the above,those interactions are elastic.

Fig.7 (Color online) Interaction between the two dark-dark soltions via Solutions (13),withp1 = 1,p2 = 3/4+1/2i,c1 = 0,c2 =?1,=0,andb(z)=z.

Fig.8 (Color online) The same as Fig.7 except thatb(z)=?2+2 sin(3z/2).

4 Conclusions

Twin-core optical fibers have been applied in such fields as the optical sensing and optical communication,and propagation of the pulses,Gauss beams and laser beams in the non-Kerr media has been reported.The coupled cubic-quintic NLS equations with variable coefficients have been investigated,i.e.,Eqs.(1),which describe the effects of quintic nonlinearity for the ultrashort optical pulse propagation in a twin-core optical fiber or non-Kerr medium.Through the KP hierarchy reduction,Dark-dark Soliton Solutions (7) have been constructed in terms of the Gramian and bilinear forms have been derived with Integrable Conditions (2).When the delayed nonlinear response effectb(z) is the constant and linear functions,the linear- and parabolic-shaped disproportional one dark-dark soltions have been displayed in Figs.1?2,respectively.Withb(z) as the linear and periodic functions and Im(p1)0,head-on interactions between the two dark-dark solitons of the parabolic- and periodic-shaped have been presented in Figs.3–4,respectively,overtaking interactions between the two dark-dark solitons of the same type have been presented in Figs.5–6,while the velocities of the two dark-dark solitons have altered withzchanging and the amplitudes of the two dark-dark solitons have been seen to remain unchanged.Besides,when Im(p1) = 0,interactions between the two dark-dark solitons of the different types have been displayed in Figs.7?8,and we have seen that the velocities of the one soliton is zero and direction of the velocity of the other soliton vary withz.Graphically analyzing the interactions between the two solitons in Figs.3?8 has indicated that those interactions are elastic.