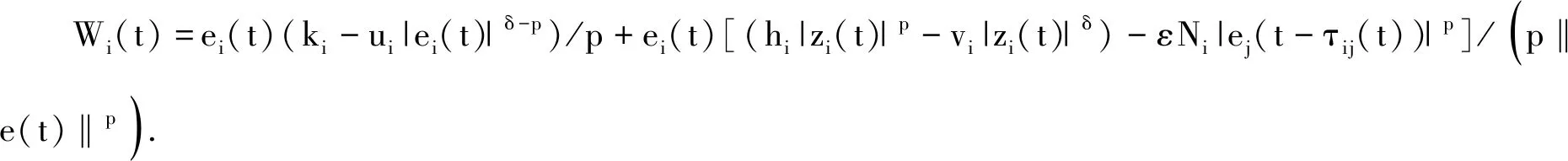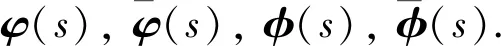蒲 浩, 冉 杰, 潘永會, 張轉周, 黃建文

(1. 遵義師范學院數學學院, 貴州 遵義 563006; 2. 西南大學數學與統(tǒng)計學院, 重慶 400715)

自競爭型神經網絡首次被提出以來, 由于競爭型神經網絡模型在不同領域有重要的應用而受到廣泛關注[1].近年來, 競爭型神經網絡的控制同步理論[2-3]以及多重因素影響下競爭型神經網絡依賴于系統(tǒng)初值在無限時間的控制同步問題[4-5]得到了廣泛研究.Shi等[5]研究了具有不同時標和反映擴散項隨機競爭神經網絡實現同步的條件; Ryan[6]提出了神經網絡依賴于初值在有限時間內穩(wěn)定性理論; Li等[7]研究了依賴于系統(tǒng)初值的混合時滯和不同擾動競爭神經網絡在有限時間內的同步.為了解決神經網絡系統(tǒng)的初值事先不能準確地獲得或很難獲得的問題, Polyakov[8]提出了獨立于系統(tǒng)初值的固定時間穩(wěn)定性理論; Wan等[9]研究了時滯Cohen-Grossberg型神經網絡的魯棒固定時間同步.本文擬通過固定時間穩(wěn)定性理論, 研究具有變時滯隨機競爭神經網絡在固定時間的控制同步.

1 模型及預備知識

考慮具有變時隨機競爭型神經網絡模型

(1)

其中n為神經元數目,p為恒定的外部刺激數目;ci為神經元時間常數;ε為短期記憶狀態(tài)的時間尺度;fj(·)表示t時刻第j個神經元的輸出量,xi(t)表示t時刻第i個神經元的狀態(tài);aij,bij分別表示第i個和第j個神經元之間的連接強度;τij(t)表示t時刻第i個神經元與第j個神經元之間的信號轉換時滯, 滿足0≤τij(t)≤τij;mil(t)表示突觸效率;Hi表示外部刺激強度;αl,βi為常數.

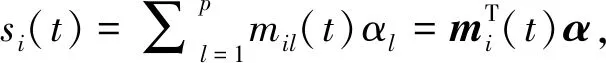
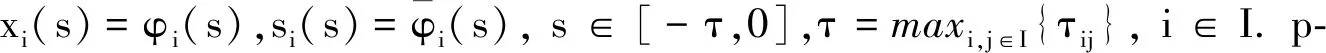
把系統(tǒng) (1) 作為主驅動系統(tǒng),并引入響應系統(tǒng)

(2)

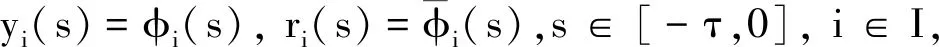
定義誤差系統(tǒng)為ei(t)=yi(t)-xi(t),zi(t)=ri(t)-si(t), 根據系統(tǒng)(1)和系統(tǒng)(2)有

為實現驅動系統(tǒng)(1)和響應系統(tǒng)(2)在固定時間同步,構造外部輸入控制Ui(t)=ei(t)(ki-ui|ei(t)|δ-p)/p+ei(t)(hi|zi(t)|p-vi|zi(t)|δ)/(p‖e(t)‖p)-ωiei(t)(|ei(t)|λ+|zi(t)|λ)/(np‖e(t)‖p)-εNiei(t)|ej(t-τij(t))|p/(p‖e(t)‖p), 其中ki,ui,hi,vi,ωi,Ni都是常數, 0<δ<1.

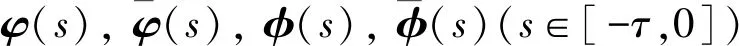
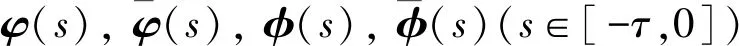
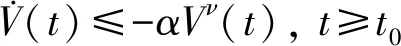
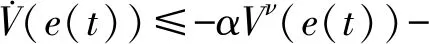
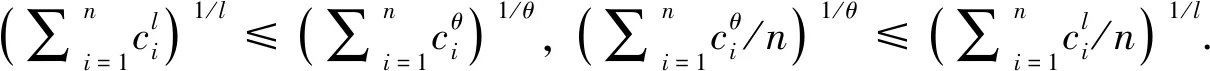
2 主要結果

定理6若(H1)(H2)成立且Xi+ki≤0,Qi+hi≤0,i∈I, 則驅動系統(tǒng)(1)和響應系統(tǒng)(2)在恰當的外部輸入控制Ui(t)下, 在固定時間T=εp/[a(p-δ)]+2λ/p-1nλ/pεp/[b(λ-p)]內同步, 其中a>0,b>0,0

注1文獻[11]是具有不同時標和隨機擾動的競爭型神經網絡, 文獻[12]是混合變時滯的隨機競爭型神經網絡, 系統(tǒng)均當時間t→+∞時才能實現自適應同步.

注2在響應系統(tǒng)(2)中存在隨機擾動項, 要使定理1中的條件Xi+ki≤0,Qi+hi≤0成立, 則需要外部輸入控制Ui(t)中的ki,hi的絕對值變得更大, 故隨機擾動項的存在對神經網絡在固定時間的同步有抑制作用.

注3文獻[13]是依賴于系統(tǒng)初值的混合時滯競爭型神經網絡在有限時間內的同步問題,由推論1可知, 文獻[13]中的結論是本文中的一種特殊情況.