E.EpelbaumJ.Gegeliaand Ulf-G.Mei?ner

2Institute for Advanced Simulation,Institut für Kernphysik and Jülich Center for Hadron Physics,Forschungszentrum Jülich,D-52425 Jülich,Germany

3Tbilisi State University,0186 Tbilisi,Georgia

4Helmholtz Institut für Strahlen und Kernphysik and Bethe Center for Theoretical Physics,Universit?t Bonn,D-53115 Bonn,Germany

1 Introduction

The chiral effective field theory(EFT)approach to few-nucleon systems[1?2]has attracted much attention during the past two and a half decades.The problem of renormalization and power counting in this framework turned out to be highly nontrivial and caused controversial debates in the community.A number of formulations alternative to Weinberg’s original proposal have been suggested to resolve the issue of renormalization,see Refs.[3–8]for review articles.In our recent paper,[9]we have compared a subtractive renormalization approach with the Wilsonian renormalization group(RG)approach[10?11]in the context of the EFT for the two-nucleon system close to the unitary limit.In particular,within the subtractive scheme,we have identi fied the choices of renormalization conditions corresponding to the Kaplan-Savage-Wise(KSW),[12]see also Refs.[13–14],and Weinberg[1]power counting schemes.The standard Wilsonian RG method with a single cuto ffscale is,on the other hand,only compatible with the KSW counting scheme.We argued that this mismatch is caused by the too restrictive formulation of the Wilsonian RG approach in its conventional form,which does not take into account the full freedom in the choice of renormalization conditions in EFT.This is the origin of the often made(incorrect,see Ref.[9])statement that the Weinberg power counting scheme for two-nucleon scattering corresponds to the expansion around a trivial fixed point.

In the Wilsonian RG approach one integrates out degrees of freedom with energies higher than some cutoffscale and systematically exploits the cuto ff-parameter dependence of coupling constants to ensure that physics at energies below the cuto ffscale remains unchanged.[15]In contrast,the Gell-Mann-Low RG equations determine the dependence of various quantities on the scale(s)of renormalization.[16]In renormalizable(in the traditional sense)theories only logarithmic divergences contribute to the renormalization of the coupling constants and,therefore,there is a direct correspondence between the two approaches. On the other hand,in EFTs with nonrenormalizable interactions,power-law divergences have to be taken care of and the direct link between the two RG equations is lost.Notice further that in theories with more than one coupling constant,as it is the case in EFTs,each coupling is attributed its own renormalization scale.In the Wilsonian approach one usually introduces a single cuto ffscale and studies how various parameters of a theory depend on it.However,in certain cases such as e.g.the few-nucleon problem in chiral EFT,it is advantageous to exploit the freedom of choosing several renormalization scales independently.[9,17]

In this paper we fill this gap and generalize the Wilsonian RG analysis of low-energy two-particle scattering in the framework of the Lippmann-Schwinger(LS)equation,pioneered in Ref.[10],by introducing a multitude of cuto ffparameters.We obtain a system of integro-differential RG equations describing the dependence of the potential on several cuto ffscales.As an application,we study a perturbative solution of the obtained system of equations for the case of two cuto ffparameters by making an ansatz for the potential in the form of a Taylor series expansion in powers of momenta.We demonstrate that the resulting potential indeed obeys the Weinberg power counting for the choice of renormalization conditions suggested in Ref.[9].

Our paper is organized as follows.In the next section we derive the system of RG equations for the case of several cuto ffparameters.In Sec.3,we present the perturbative solution of this system of equations and discuss the obtained results in the context of EFT for two-nucleon scattering.Finally,our main findings are brie fl y summarized in Sec.4.

2 The Lippmann-Schwinger Equation with a Multitude of Cuto ffParameters

To introduce a multitude of cuto ffparameters and derive the corresponding system of RG equations we start with the fully o ff-shell LS equation

whereG(k,l)=2m/(k2?l2+i?)is the nonrelativistic two-particle Green’s function,andk2/mis the kinetic energy in the centre-of-mass frame.We assume that the low-energy dynamics of the system at hand is describable in the framework of the non-relativistic Schr?dinger theory,i.e.that the underlying potentialV(p,q,k)is non-singular and well-behaved in the quantum mechanical sense.We regard Eq.(1)as an “underlying” model and follow the philosophy of Wilson’s renormalization group approach.Speci fically,we aim at integrating out the high-momentum modes by introducing 2N cutoffssuch that the o ff-shell amplitude remains unchanged at low-energies.While in all practical applications one considers Hermitean cuto ffpotentials,corresponding to,to keep our resulting equations in the most general form we do not impose this condition in our derivation.We start by writing the potentialV(p,q,k)as a sum of various contributions(the choice of which depends on the particular problem one is dealing with)

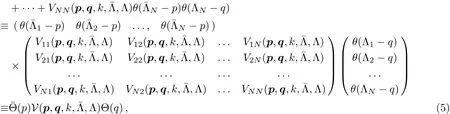
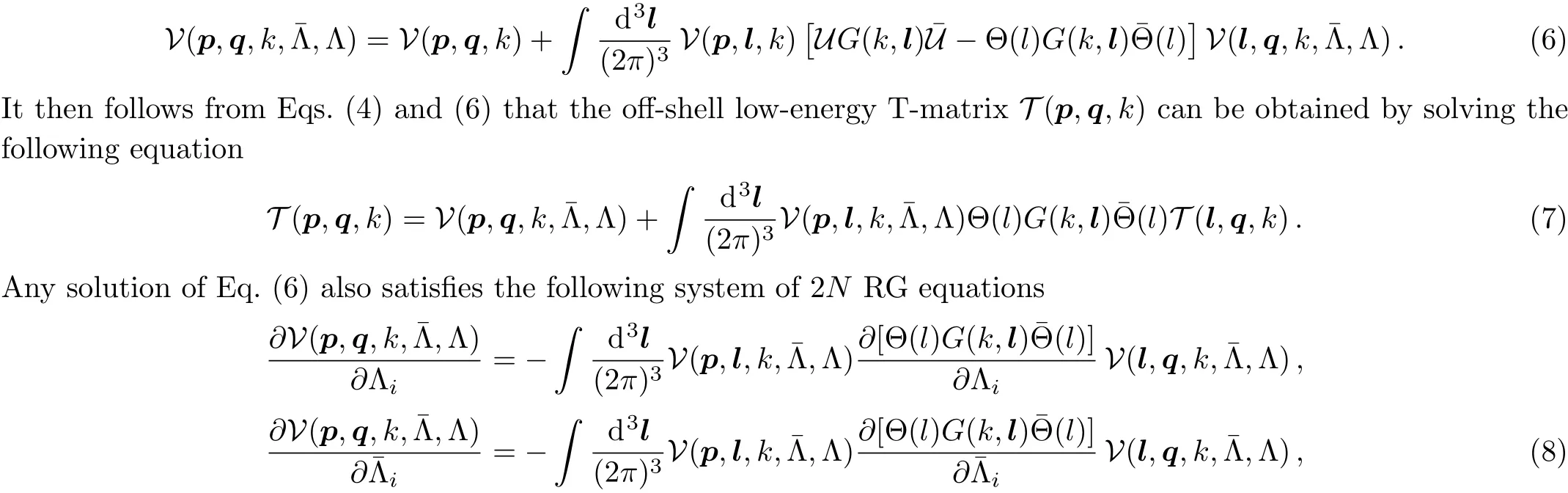
withi=1,...,N.While the above derivation of Eq.(8)served mainly for the purpose of demonstrating of its physical content,it can be directly obtained from Eq.(7)by demanding cuto ffindependence ofTherefore,forsatisfying Eqs.(8),the o ff-shell amplitudeobtained from the solution of Eq.(7)is cuto ffindependent and coincides with the solution of Eq.(1)at low energies,i.e.below all cutoffs Λiand

The case of Hermitean cuto ff-dependent potentials corresponds to choosingFurthermore,for a single cuto ffparameter,Eq.(8)reduces to the differential RG equation of Ref.[10].In general,Eq.(8)is a system of integro-differential equations,however in some cases such as e.g.for separable potentials,it can be reduced to a system of differential equations.

3 RG Equation with Two Cutoffs

In exact analogy to the previous section,one can obtain a system of RG equations for the LS equation in partial wave basis

Here and in what follows,we restrict ourselves to the case of Hermitean potentials.

As a simple application,we solve the RG equations with two cuto ffparameters,as a perturbative power series expansion in the small parameters,p,q,k,and Λ2.Speci fically,we consider the cuto ffregularized potential of the form

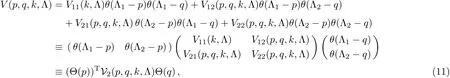
The functionsC1,C2,andC3are analytic atk2=0,i.e.they can be written as Taylor series

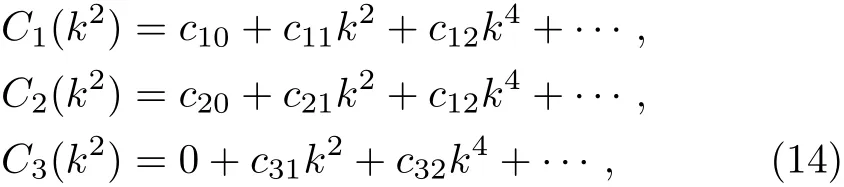
where we have takenC3with a vanishing constant term in order that the NLO potential is indeed suppressed by powers of small parameters.All parameters of the potential cannot be fixed by demanding that the empirical on-shell scattering amplitude is reproduced.Therefore,we set all coefficients to zero except forc10,c20andc31.We fix the remaining constantsc10andc31by matching to the low-energy scattering amplitude parameterized in the form of the effective range expansion

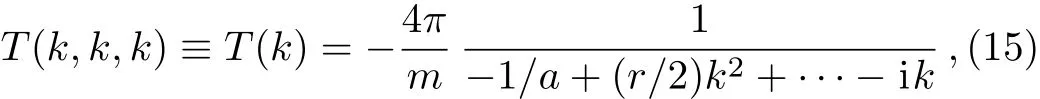
withmthe particle mass,athe scattering length andrthe effective range.We write Eq.(15)as a perturtbative expansion valid both for the case of a natural and unnaturally large scattering length,

The coefficientc20remains undetermined and parameterizes the remaining freedom in the choice of the o ff-shell potential.

Substituting the obtained values ofcijback into the potential,we find

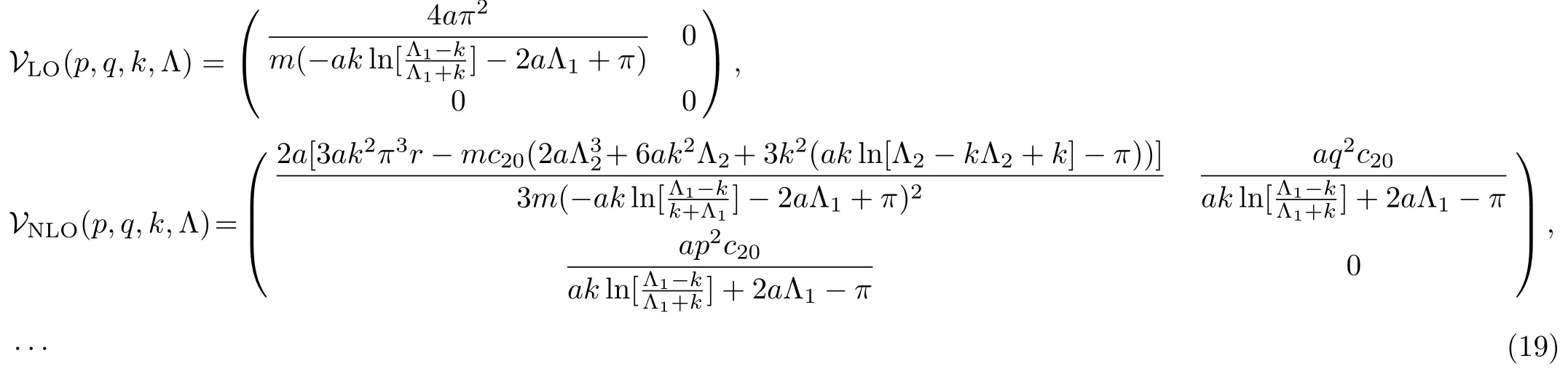
4 Summary and Conclusions

Our paper provides a generalization of the Wilsonian renormalization group approach to the Lippmann-Schwinger equation for two-particle scattering at low en-ergy by introducing a multitude of cuto ffparameters.We derive a system of integro-differential equations for the cuto ffregularized potential,which reduces to the RG equation of Ref.[10]for the case of a single cuto ff.As a simple application,we considered a perturbative solution of the system of RG equations in the form of a power series expansion in momenta and energy.We have demonstrated that by introducing two cuto ffparameters,one obtains a perturbative expansion of the potential which follows the Weinberg power counting rules,[2]while as shown in Ref.[10],the usage of a single cuto ffparameter leads to the power counting of Refs.[12–14].This simple example demonstrates that the enlargement of the space of the renormalization group parameters by exploiting the full freedom in the choice of renormalization conditions can be advantageously used in the context of the low-energy EFT for nucleon-nucleon scattering.It will be interesting to apply the presented formalism with the multitude of cuto ffparameters to the case of the potentials with a long-range interaction.This work is in progress.

EE and JG are grateful to M.Birse for useful discussions on the Wilsonian RG approach.

[1]S.Weinberg,Phys.Lett.B 251(1990)288.

[2]S.Weinberg,Nucl.Phys.B 363(1991)3.

[3]P.F.Bedaque and U.van Kolck,Ann.Rev.Nucl.Part.Sci.52(2002)339.

[4]E.Epelbaum,H.W.Hammer,and Ulf-G.Mei?ner,Rev.Mod.Phys.81(2009)1773.

[5]M.C.Birse,PoS CD 09(2009)078.

[6]E.Epelbaum and Ulf-G.Mei?ner,Ann.Rev.Nucl.Part.Sci.62(2012)159.

[7]R.Machleidt and D.R.Entem,Phys.Rept.503(2011)1.

[8]M.P.Valderrama,Int.J.Mod.Phys.E 25(2016)1641007.

[9]E.Epelbaum,J.Gegelia,and Ulf-G.Mei?ner,Nucl.Phys.B 925(2017)161.

[10]M.C.Birse,J.A.McGovern,and K.G.Richardson,Phys.Lett.B 464(1999)169.

[11]K.Harada,H.Kubo,and Y.Yamamoto,Phys.Rev.C 83(2011)034002.

[12]D.B.Kaplan,M.J.Savage,and M.B.Wise,Phys.Lett.B 424(1998)390.

[13]U.van Kolck,Lect.Notes Phys.513(1998)62.

[14]U.van Kolck,Nucl.Phys.A 645(1999)273.

[15]K.G.Wilson and J.B.Kogut,Phys.Rept.12(1974)75.

[16]M.Gell-Mann and F.E.Low,Phys.Rev.95(1954)1300.

[17]J.Gegelia,Phys.Lett.B 463(1999)133.