Da-Jun Liu(劉大軍),Yao-Chuan Wang(王耀川),Gui-Qiu Wang(王桂秋),Hong-Ming Yin(尹鴻鳴),and Hai-Yang Zhong(仲海洋)

Department of Physics,College of Science,Dalian Maritime University,Dalian 116026,China

Keywords:oceanic turbulence,multi-Gaussian Schell-model source,edge dislocation,laser propagation,average intensity.

1.Introduction

The properties of laser beams propagating in underwater oceanic turbulence were widely investigated due to their applications in wireless optical communications and laser sensing.So far,the power spectrums of oceanic turbulence have been introduced by many researchers.[1,2]Until now,a variety of laser beams propagating in turbulent ocean have been studied based on the power spectrum of oceanic turbulence.The evolution properties of coherent laser beams propagating in oceanic turbulence have been studied,such as higher order mode laser beam,[3]Lorentz beam,[4]Lorentz Gauss beam,[5]Lommel–Gaussian beam,[6]Gaussian beam,[7]Gaussian pulsed X wave,[8]radially polarized beam,[9]vector beam,[10]rotating elliptical chirped Gaussian vortex beam,[11]ultra-short pulse,[12]Gaussian array,[13,14]and chirped Gaussian pulsed beam.[15]On the other hand,it can be found that partially coherent beams have advantage over fully coherent beams for mitigating the effect of turbulence.[16]The evolution properties of various partially coherent beams propagating in oceanic turbulent were discussed,such as partially coherent flat-topped vortex hollow beam,[17]partially coherent Lorentz–Gauss beam,[18]partially coherent Lorentz–Gauss vortex beam,[19]stochastic beams,[20]astigmatic stochastic electromagnetic beam,[21]partially coherent four-petal Gaussian beam,[22]partially coherent four-petal Gaussian vortex beam,[23]partially coherent Hermite–Gaussian linear array beam,[24]radial phase-locked partially coherent Lorentz–Gauss array beam,[25]radial phase-locked partially coherent standard Hermite–Gaussian beam,[26]phase-locked partially coherent radial flat-topped array laser beam,[27]Gaussian Schell-model vortex beam,[28]stochastic electromagnetic vortex beam,[29]partially coherent anomalous hollow vortex beam,[30]multi-Gaussian Schell-model beam,[31]rectangular multi-Gaussian Schell-model beam,[32]electromagnetic multi-Gaussian Schell-model beams with astigmatic aberration,[33]stochastic electromagnetic higher-order Bessel–Gaussian beam,[34]optical wave and short-term beam,[35]and random electromagnetic multi-Gaussian Schellmodel vortex beam.[36]The beams generated by the multi-Gaussian Schell-model(MGSM)source can evolve into the flat-topped beam as the propagation distance increases.[37]It is very interesting to ask what will happen if the MGSM beam carries an edge dislocation.Thus,we will firstly introduce the model of multi-Gaussian Schell-model(MGSM)beams carrying an edge dislocation,and then discuss the evolution properties of the MGSM carrying an edge dislocation propagating through oceanic turbulence in this paper.

2.Model of MGSM beams carrying an edge dislocation

In the Cartesian coordinate system,the electric field of a Gaussian beam with an edge dislocation at the plane z=0 takes the form[38]

where p and d are the slope and off-axis distance of the edge dislocation,is the positon vector,w0xand w0yare the beam waist of the Gaussian beam along the x and y directions.

Considering the multi-Gaussian Schell-model source,[37]the cross-spectral density(CSD)of the MGSM beams carrying an edge dislocation can be expressed as

3.Analytical expressions of MGSM beams carrying an edge dislocation in oceanic turbulence

Based on the extended Huygens–Fresnel principle,the CSD of the partially coherent beam propagating in oceanic turbulence can be expressed as[17–30]

where k=2π/λ is the wave number,λ is the wavelength,(j=1,2)is the position vector at plane z,andis the random part of complex phase of the spherical wave propagating in turbulence.In Eq.(4),we can write

where ε denotes the rate of dissipation of kinetic energy per unit mass of fluid,χTdenotes the rate of dissipation of meansquared temperature,? denotes a unitless parameter providing the ratio of temperature to salinity contribution to the refractive index spectrum,which varies in the range from ?5 to 0 and refers to the dominating temperature and salinityinduced oceanic turbulence,respectively,and η is the Kolmogorov micro scale(inner scale).The other parameters are AT=1.863×10?2,AS=1.9×10?4,ATS=9.41×10?3,and δ=8.284(κη)4/3+12.978(κη)2.

In Eq.(5),we can define the coherence length as

Submitting Eq.(2)into Eq.(4),and considering the following equation:

we can derive the CSD of the MGSM beam carrying an edge dislocation propagating in oceanic turbulence as

where

with

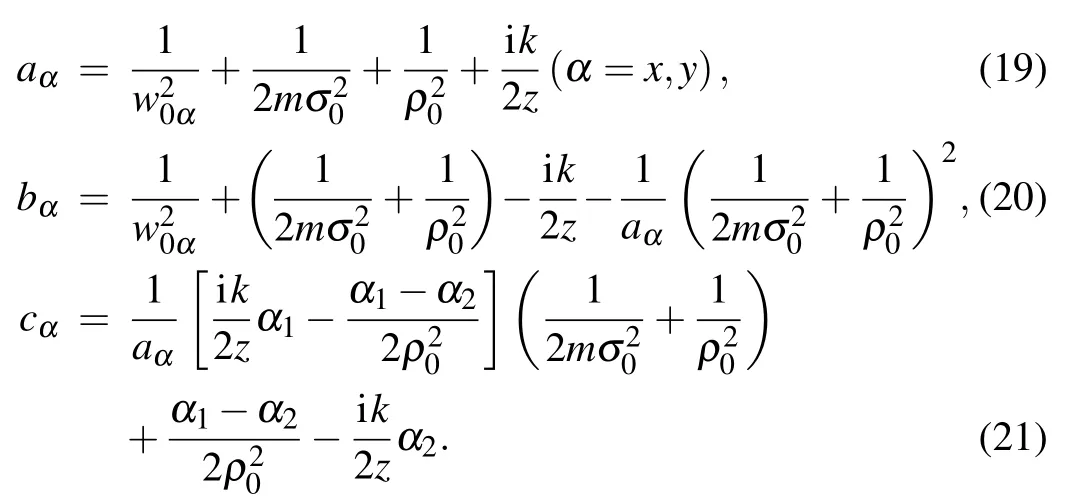
The average intensity of the MGSM beam carrying an edge dislocation propagating in oceanic turbulence can be obtained by[39]

The spectral degree of coherence of two pointsandin the MGSM beam carrying an edge dislocation propagating in oceanic turbulence at plane z can be written as[39]

4.Numerical examples and analysis

Here the propagation properties of the MGSM beam carrying an edge dislocation in free space and oceanic turbulence are investigated by using the derived analytical equations in the above section.In the numerical calculations,the parameters are selected as λ=417 nm,w0x=w0y=1 cm,σ0=1 mm,M=50,p=2,d=1 mm,χT=10?8K2·s?1,ε=10?7m2·s?3and ?=?2.5 unless specified in the captions of figures.

During the coherence length ρ0=∞in Eq.(7),the propagation equations of the MGSM beam carrying an edge dislocation in oceanic turbulence will reduce to the propagation equation in free space.The evolution properties of the MGSM beam carrying an edge dislocation propagating in free space are studied in Fig.1.The results indicate that the two intensity peaks of the MGSM beam carrying an edge dislocation will overlap with each other as the propagation distance increases(Figs.1(a)and 1(b));in the far field,the MGSM beam carrying an edge dislocation propagating in free space will evolve from the beam with two peaks into a flat-topped beam introduced by the MGSM source,the beam intensity profile of the MGSM beam carrying an edge dislocation in the far field is similar with that of the MGSM.[40]Thus,the effects of the edge dislocation on the average intensity of the MGSM beam in free space disappear in the far field.

The cross sections of the MGSM beams carrying an edge dislocation propagating in free space for different M and σ are plotted in Figs.2 and 3,respectively. One can find that the MGSM beams carrying an edge dislocation with the larger M and smaller σ can remain the flat-topped profile better in the far field,and when M=1,the intensity profile is the GSM carrying an edge dislocation(red line in Fig.2).

Fig.2.Cross sections of MGSM beams carrying an edge dislocation propagating in free space for different M:(a)z=100 m,(b)z=300 m.

Figure 4 shows the average intensity of the MGSM beams carrying an edge dislocation propagating in oceanic turbulence.One can find that the MGSM beams carrying an edge dislocation propagating in oceanic turbulence will evolve into a beam with a smaller flat-topped profile than the beam propagating in free space(Fig.1(d))due to the influences of the oceanic turbulence.The reason is that the general beam propagation in turbulent medium will all evolve into the Gaussian beam.[41]Thus,the MGSM beams carrying an edge dislocation propagating in oceanic turbulence will become a beam with a smaller flat-topped profile.

Fig.3.Cross sections of MGSM beams carrying an edge dislocation propagating in free space for different σ:(a)z=100 m,(b)z=500 m.

Fig.4.Average intensity of MGSM beams carrying an edge dislocation propagating in oceanic turbulence:(a)z=100 m,(b)z=300 m.

The cross sections of the MGSM beams carrying an edge dislocation propagating in oceanic turbulence are given in Figs.5 and 6 for different p and d,respectively.From Figs.5 and 6,we can see that the MGSM beams carrying an edge dislocation with the larger slop p or smaller off-axis distance d propagating in oceanic turbulence will evolve into a Gaussianlike beam faster(Figs.5(a)and 6(a)),and as the propagation distance increases,the influences of the different p and d on the profile of the beam in the far field will disappear(Figs.5(b)and 6(b)).

Fig.5.Cross sections of MGSM beams carrying an edge dislocation propagating in oceanic turbulence for different p:(a)z=50 m,(b)z=200 m.

To obtain the influences of oceanic turbulence on the spreading properties of the MGSM beam,we illustrate in Figs.7 and 8 the cross sections of the MGSM beams carrying an edge dislocation propagating in oceanic turbulence for different χT,?,and ε,respectively.One can see that the MGSM beams carrying an edge dislocation propagating in oceanic turbulence with the larger χTand ? or the smaller ε will evolve into the flat-topped beam or a Gaussian beam as the propagation distance increases.The strength of oceanic turbulence is stronger when the oceanic turbulence parameters χTand ? are larger or ε is smaller.Thus,the MGSM beam propagating in stronger oceanic turbulence will evolve into the flat-topped beam or a Gaussian beam at the shorter propagation distance.

Fig.6.Cross sections of MGSM beams carrying an edge dislocation propagating in oceanic turbulence for different d:(a)z=50 m,(b)z=200 m.

Fig.7.Cross sections of MGSM beams carrying an edge dislocation propagating in oceanic turbulence for different χT:(a)z=100 m,(b)z=300 m.

Fig.8.Cross sections of MGSM beams carrying an edge dislocation propagating in oceanic turbulence at propagation distance z=300 m:(a)different ?,(b)different ε.

Fig.9.Spectral degree of coherence of MGSM beams carrying an edge dislocation propagating in oceanic turbulence at propagation distance z=100 m:(a)different p,(b)different d.

The spectral degrees of coherence of the MGSM beams carrying an edge dislocation propagating in oceanic turbulence for different p,d,and M are given in Figs.9 and 10,respectively.As can be seen,the spectral degrees of coherence of the MGSM beams carrying an edge dislocation can be modulated by the distance between two points.And it is also seen that the position of coherence vortex(μ=0)of the MGSM beams carrying an edge dislocation propagating in oceanic turbulence can be obtained at the smaller distance between two points for the larger p or smaller d(Fig.9).In studied of influences of M on the spectral degrees of coherence,one can find that the influences of different M on the spectral degree of coherence will gradually disappear as the propagation distance increases(Fig.10(b)).

Fig.10. Spectral degree of coherence of MGSM beams carrying an edge dislocation propagating in oceanic turbulence for different M:(a)z=20 m,(b)z=100 m.

5.Conclusion

The model of MGSM beams carrying an edge dislocation has been introduced,and the evolution properties of MGSM beams carrying an edge dislocation propagating in oceanic turbulence have been investigated using the numerical examples.It is shown that the MGSM beam carrying an edge dislocation propagating in oceanic turbulence will evolve from the profile with two intensity peaks into a flat-topped beam caused by the MGSM source,and the beam will evolve into the flat-topped beam with smaller beam spot or the Gaussian-like beam due to the influences of the oceanic turbulence in the far field,and the MGSM beams carrying an edge dislocation propagating in oceanic turbulence with the larger χTand ? or the smaller ε evolve into the flat-topped beam or a Gaussian beam faster as the propagation distance increases. It is also shown that the position of coherence vortex can be obtained at the smaller distance between two points for the larger slop p or smaller off-axis distance d.As the propagation distance increases,the influences of different M on the spectral degree of coherence will gradually disappear.