Yuan-Yuan Li(李院院),Li Li(李莉),Yun-Zhe Zhang(張云哲),and Lei Zhang(張雷)

Institute of Physics,Xi’an University,Xi’an 710065,China

Keywords:four-wave-mixing,dynamic control,inner-dressing

1.Introduction

The suppression and enhancement of four-wave-mixing(FWM)process in electromagnetically induced transparency(EIT)windows[1–8]can be implemented in many multi-level systems, such as ladder-type,[2,9,10]Y-type,[8]and double lambda-type[4–6,11–13]level configurations. In a ladder-type system with hyperfine ground states,the magnitude of FWM signal is found to be dependent on the transition route,and dominantly related to the residual two-photon coherence according to the degree of optical pumping to the other ground state.[9]While these features in the cycling transition are dramatically influenced by ladder-type and V-type two-photon coherence components,respectively.[9]Highly efficient FWM and six-wave mixing(SWM)signals coexisting in EIT windows were reported in an open four-level Y-type atomic system,in which the interplay between these two nonlinear processes is due to three-and five-photon destructive interferences.[8]Recently,in a backward double-lambda system,the conversion efficient in cold rubidium atoms was observed to be 63%,and the conversion efficient was predicted to be 96%by using a medium with a large optical depth.[13]

The control of FWM process can be achieved by changing several parameters of the fields applied to the system,e.g.,the detuning and the strengths,[8,14]the relative phases,[15]and the pulse dynamics.[16]This control of FWM process can be applied to the quantum entanglement,[17]the fabrication of scalable multimode quantum resources,[18]and the enhancement of bright-seeded SU(1,1)interferometer.[19,20]In the present work,we consider a reverse Y-type atomic system driven by one probe and two coupling fields.The probe field is periodically modulated by a phase function.The two coupling fields are involved in both FWM and dressing process,thus we term the coupling fields inner-dressing fields hereafter. We will show that the FWM process can be successfully controlled by selecting different dynamic parameters of the probe field,and strengths of the inner-dressing fields.We will also show that the controllable FWM process is dominantly influenced by the evolution of atomic population difference and two-photon coherence.This type of dynamic and inner-dressing control of FWM can be probably used in optical information processing.

2.Theoretical model

A reverse Y-type four-level atomic system is shown in Fig.1(a),whereandare selected as hyperfine levels with a splitting differenceandare the intermediate and the excited states of the atom,respectively.Beams diagram is shown in Fig.1(b),where beam 1 represents a weak probe field ε1,while beams 2 andpropagating with a small angle difference(～0.5?)represent strong inner-dressing fields ε2andrespectively. The transition frequency ofandare ?1,?2,and ?3respectively.The frequency,the detuning,the Rabi frequency and the wave vector of the fieldare denoted as ωi,,and(i=1,2,3)respectively.The ε1is assumed to be periodically modulated by a phase function φ(t)=Asin(νt),where A and ν are the modulation amplitude and frequency,respectively.[21]If the phase-matching conditionis satisfied,the FWM signal propagating in the direction almost opposite to the beam 2can be generated.

Fig.1.Diagram of(a)energy levels and(b)beam configuration in reverse Y-type four-level system.

The FWM signal is governed by the third-order density matrix elementsandConsidering thatexhibits almost the same feature aswe calculate only the density matrix elementby using the following coupling equations:

where the complex detuningswith(i,j=0,1,2,3,ij);the decay rate from leveltois defined aswith Γi(Γj)being the decay rates of level

To obtain the above coupling equations,we assume that g3=g1andIt is obvious that the modification ofis mainly influenced by the evolution of population differencetwo-photon coherencesandTo solve these coupling equations,Fourier expansion of the field ε1is usually used to find the resonant components involved in the coupling of relative transitions.[19]However,this method is cumbersome and incomplete for solving the dynamic and inner-dressing problem.In the following discussion,we numerically solve the above coupling equations by using the algorithm developed in Refs.[21]and[22].

To simplify the calculation,the atoms are assumed to be initially populated at the ground statei.e.,and=0(i=j=1,2,3),one can obtain immediatelyThe coupling equations(3)–(6),and(8)are reduced to Eqs.(11)–(14),and(15)respectively:

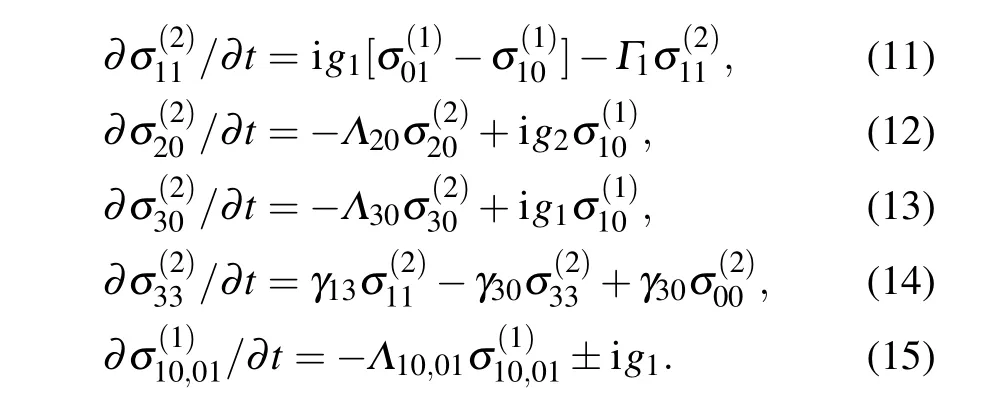
The FWM signal is proportional to the third-order density matrix elementwhich can be obtained by numerically solving Eqs.(1),(2),and(11)–(15).In the following,we analyze these numerical results of FWM signals modified by dynamic parameters of the probe field,and the strength of the inner-dressing fields.

3.Numerical results and discussion

Parameters of85Rb atom corresponding to possible experiments are chosen in our numerical calculation,where 5S1/2(F=2),5S1/2(F=3),5P1/2,and 5D1/2levels are corresponding to statesandrespectively. These resonances at the structure are feasible to accomplish a chipscale setup,which have a great practical importance.At the same time the harmonic phase modulation(frequency deviation)of miniature semiconductor laser(so-called VICSEL)is ordinarily used in practice.[23]The decay rates are γ10,13=2π×3 MHz,γ21=2π×0.8 MHz,γ30=2π×1 kHz,γ20,23=0,and Γ1=2π×6 MHz,respectively.It is assumed that the probe field ε1is always very weak,with taking g1=g3=0.01γ10,the strengths of the inner-dressing fields ε2andare much greater than that of the probe field.We also assume that the dressing fields are detuned exactly totransition,i.e.,?2=0.Considering that ?3satisfies(Fig.1(a)),we are concerned about only the detuning ?1in the following.A typical modulation frequency is usually ν=?/2,and the FWM lines versus ν around ?/2 are examined in all cases.

We consider first the case that the strengths of the inner-dressing fields are far less than γ10,with taking g2==0.3γ10.In this case,both coherent population trapping(CPT)[24]in lambda-type sub-systemand EIT in ladder-type sub-systemcontribute to the formation of a dark state,and FWM signals can transmit in the medium almost without any absorption.The FWM lines are shown in Fig.2 for the different probe detuning values:?1=0.46,0.48,0.50,0.52,and 0.54(in units of ?),respectively,where the modulation index A=1.The peaks of these lines are at the resonant position of ν=?1,i.e.,if ω1is detuned away fromtransition with a value of ?1,a probe field with a modulation frequency ν=?1can introduce an enhanced FWM process at ω=ω1+?1. When the modulation frequency ν is tuned to a fixed value ?/2,the peak values of these signals exhibit a damped oscillation behavior(Fig.3(a)),which indicates that the FWM process can be optimized by appropriately choosing modulation frequency and indices. To verify this,FWM lines are plotted in Fig.3(b)for A=0.5,0.8,1,1.95,2.5,and 3,respectively.It is shown apparently that the FWM signals can be controlled by choosing different modulation parameters of the probe field.

Fig.2. Plots of FWM lines versus modulation frequency ν near ?/2 for different probe detuning values:?1/?=0.46,0.48,0.50,0.52,and 0.54,respectively.Other parameters are A=1,

Fig.3. (a)Modulation index-dependent peak amplitude of FWM lines at ν=?/2;(b)FWM lines varying with ν for A=0.5(square),0.8(solid circle),1(upward triangle),1.95(downward triangle),2.5(rhombus),and 3(leftward triangle),respectively.Other parameters are ?1/?=0.5,

Fig.4.Modulation-dependent FWM lines for relative larger inner-dressing strength:(a)and(b)for different dressing strengths (square),1(solid circle),1.5(upward triangle),2(downward triangle),and 3(rhombus),respectively;the probe detunings for panels(a)and(b)are ?1/?=0.5 and 0.48,respectively;(c)for different modulation frequencies ν/?=0.46(square),0.48(solid circle),0.5(upward triangle),0.52(downward triangle),and 0.54(rhombus),respectively;and(d)for different modulation amplitudes A=1(square),1.8(solid circle),and 3(upward triangle),respectively.Other parameters are taken as A=1 in panels(a),(b)and(c), in panel(c),and ν/?=0.5 in panel(d),respectively.

Next,we examine the modulation dependent FWM lines for relative larger inner-dressing strength(Figs.4(a)–4(d)).In this case,the EIT in ladder-type sub-systemdominantly contributes to the formation of a dark state,and FWM signals transmit in the EIT windows. Figures 4(a)and 4(b)show FWM lines for the inner-dressing strengths1,1.5,2,and 3(in γ10units),respectively,where the modulation index A=1,and the probe detuning for Figs.4(a)and 4(b)are ?1=0.5 and 0.48(in units of ?),respectively. It can be found that an increasing dressing intensity can suppress FWM signals at the resonant frequency of ν=?1.As the dressing strength becomes greater than γ10,a largely suppression of FWM signal happens at ν=?1,and several enhanced peaks can be observed at ν=?1±γ10p/2(p=1,2,3,...).As shown in Fig.4(c),this type of suppression and enhancement of FWM signals can persist for different probe detuning values:?1=0.46,0.48,0.50,0.52,and 0.54(in units of ?).One can find that the red detuning of the probe field can introduce a larger suppression of FWM signals when the resonant condition ν=?1is satisfied.The modulation index A can also dramatically modify FWM signals in a strong coupling regime(Fig.4(d)).The greater the peak amplitude,the larger the suppression at the resonant position will be.We believe that this suppression of FWM signals results dominantly from destructive interference between two channels induced by inner-dressing fields,[14]while the enhancement of FWM signals is induced by both dynamic parameters of the probe field and the strong inner-dressing effect.

The controllable FWM signals can be explained by analysing the evolution of atomic level population difference and two-photon coherences.As stated,this evolution of FWM signals is mainly influenced by population difference ?σ,twophoton coherencesandHowever,is of third order and less thanin our calculation,thus the modification of FWM process is influenced dominantly by ?σ andAn increasing coupling intensity will suppress the FWM signals at resonant position,while an enhanced contribution induced by the population change can counteract part of the suppression,e.g.,the peak amplitude for g2=0.6γ10is larger than that for g2=γ10.

As the dressing strength is greater than γ10,is dominantly determined by two-photon coherence,since g1?σ is far less thanIn this case,the signal features can be explained by analysing the evolution of. The real(imaginary)part ofis shown in Figs.5(a)(5(b))and 5(c)(5(d))for different coupling strengths and modulation indices,respectively.Where the parameters used in Figs.5(a)(5(b))and 5(c)(5(d))are corresponding to Figs.4(a)and 4(d),respectively.At ν=?1,the imaginary part ofis zero,and the FWM process is governed mainly by the real part ofwhich gives rise to a largely suppression of FWM signals for an increasing dressing strength.As the modulation frequency is detuned away from the resonant position,the real part of this coherence decreases fast to zero,and then changes to a gain region with a damped oscillation behaviour,both the real part and imaginary part contribute to the splitting of peaks and the oscillation fringes. A similar evolution process can also be observed in the change of modulation index A as shown in Figs.5(c)and 5(d).Thus,the control of FWM process can be achieved by tuning the dynamic parameters of the probe field and strengths of the inner-dressing fields.

Fig.5.Plots of real and imaginary part of versus ν for different values of((a),(b))g2 and((c),(d))A.Parameters in panels(a)–(d)are corresponding to those in Figs.4(a)–4(d)respectively.

Here we should point out that this dynamic and innerdressing controlling method suffers the competition between EIT and CPT induced by probe and coupling fields,and by the modulation of the probe field as well,respectively. It is different from the process in the out-dressing system investigated in Refs.[25]–[28]where the control process is achieved mainly by the modulation of electromagnetically induced gratings(EIG)formed by the dressing fields via switching between bright and dark states.

4.Conclusions

We theoretically investigate the FWM process in a periodically-driven atomic system.It is shown that an increasing dressing intensity can suppress FWM signal at the resonant position of ν=?1.As the dressing strength becomes greater than γ10,the almost totally suppression of FWM signals can happen at the resonant position,accompanied by several enhanced peaks at ν=?1±γ10p/2. This dynamic and innerdressing control of FWM process is influenced dominantly by the evolution of atomic population difference and two-photon coherence,and can be probably used in optical information processing.By comparing with the advantages of the closed lambda-type system,N-type system and ladder-type system,the advantage of a reverse Y-type system in our discussion can be used to accomplish the coexistence of FWM and SWM processes since the former can be suppressed and the latter can be enhanced.[8,14]