Hua-Nan Li(李化南),Zi-Wei Fan(笵紫薇),Jia-Xin Li(李佳欣),Yue Hu(胡月),and Hui-Lian Liu(劉惠蓮)

College of Physics,Jilin Normal University,National Demonstration Center for Experimental Physics Education,Jilin Normal University,Siping 136000,China

Keywords:magnetic vortex,spin-polarized current,point-contact,micromagnetic simulation

1.Introduction

Magnetic vortex(MV)often exists in nanodisks made of soft ferromagnetic materials,which can be characterized by an out-of-plane polarity and an in-plane chirality.[1,2]The MV has received much attention for its technological applications in spin-transfer-torque magnetic random access memories,logical devices,and nano-oscillators because of its unique dynamical behaviors.[3–10]In order to apply MV to new spintronic devices,the key point is to control the dynamic properties of MV such as the polarity reversal,chirality reversal,and gyration.[4,11–19]Recently,we investigated the polarity reversal mediated by a spin-polarized current in a confined geometry,finding that not only the MV can be easier triggered but also the polarity can be reversed with a lower current density and using less time if the point-contact is not designed in the nanodisk center.[20,21]Furthermore,our research found that the position and the size of point-contact can control the eigenfrequency of MV gyration.[15,22,23]Taking into account the previous studies and considering the better application of MV,[24]we particularly focus on the MV gyration in permalloy(Py)nanodisks with different sizes in this paper and investigate the effects of the point-contact position on MV gyration,including the critical current density of MV gyration,eigenfrequency,trajectory,velocity,and the time for a magnetic vortex to obtain the steady gyration.diameter 2R is set to range from 400 nm to 600 nm with its thickness L changing from 15 nm to 35 nm.The initial magnetic state of nanodisks with these sizes is MV denoted by(p,c)=(1,1),where p=1 indicates the+z direction of the polarity and c=1 refers to the counterclockwise direction of the chirality.The current is injected into Py nanodisks through point-contact,and the diameter of point contact is fixed at 100 nm.Moreover,the point-contact is not located at the disk center and the distance between its center and the center of the disk is d.In order to conveniently demonstrate the influence of the point-contact position on the MV gyration,we define Rd=d/R in this work.

Fig.1. Schematic diagram of a model system. Permalloy nanodisks of radius R and thickness L are used as model system and polarized current is applied via a point-contact represented by a white cylinder with radius Rc.Point-contact is located at y axis and its center distance from the disk center is d.Red arrow ip=1 and blue arrow Sp=?1 refer to+z and ?z directions of applied current and spin polarization,respectively.

2.Simulation details and results

In this work,we pay our attention to the MV gyration in Py nanodisks with different sizes as shown in Fig.1.The disk

Magnetization simulation calculation is performed by OOMMF based on Landau–Lifshitz–Gilbert(LLG)equation with spin-transfer-torque(STT)and Oersted field induced by the current,[18,19,25]

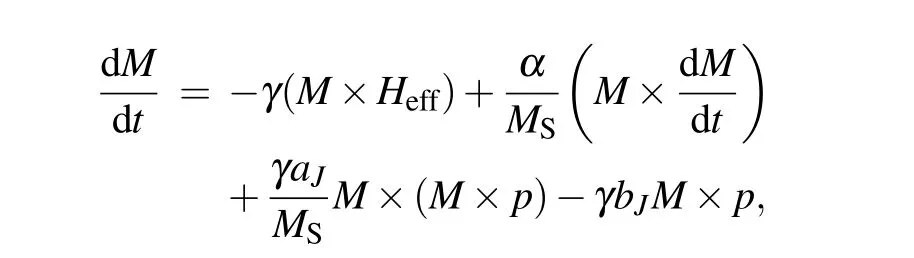
where M=mMsis the magnitude of magnetization vector of the MV,m is the magnitude of unit magnetization vector,Msis the saturation magnetization,Heffis the effective fields including the external magnetic field,anisotropy field,demagnetizing field,exchange field,dipolar field generated by the out-of-plane magnetic polarizer,and γ is the gyromagnetic ratio.The first term on the right-hand side of the LLG equation describes the Larmor precession of magnetization,the second term is the Gilbert damping term,α is the damping factor,the third and fourth term are the in-plane Slonczewiski’s spin torque[26]and field-like spin torque,[27–29]respectively.The simulation Py material parameters are as follows:the exchange constant A=1.3×10?11J/m,P is the spin polarization and set to be 0.4,Ms=8.6×105A/m,α=0.5 and the unit cell is 2.5×2.5×L nm3.[25,26]

Fig.2.Plots of critical current density of gyration jg versus Rd(a)for nanodisks with the same R and different values of L,and(b)for the nanodisks with the same L and different values of R.

Firstly,we should confirm the minimum value of the current density that can trigger the MV gyration in different nanodisks,and this value is defined as critical current density jg.Figure 2(a)shows the dependence of jgon Rdin the disks with the same radius and different thickness values.It is clear that jgin the thicker disks is much higher than that in the thinner disks,indicating that the MV in thinner disks can develop gyrotropic motion at a lower current density.We also observed that the differences among jgvalues gradually become larger when the Rdis further increased.For example,the value of jgis 12×1011A/m2in the disk of L=15 nm,whereas the jgvalue reaches to 28×1011A/m2in the disk of L=35 nm at Rd=0.75.However,their discrepancy is only 5×1011A/m2at Rd=0.025.Therefore it is concluded that the smaller Rdis more advantageous for the MV gyration,and the point-contact positions of Rd<0.4 can be considered as the appropriate positions for MV gyration because jgincreases drastically when Rdis over 0.4.Indeed,our previous researches demonstrated that the MV can be pinned when the point-contact is placed far enough at the smaller current density.[24]For the MV in the nanodisks with the same thickness and different radii,the situation is rather different as shown in Fig.2(b).It is found that the differences among jgare much smaller in these disks,implying that jgis more sensitive to the thickness.It is thereby derived that the MV in thinner and larger disks is more beneficial to MV gyration.

Fig.3.Plots of eigenfrequency versus current density j for(a)the same R and different values of L,for(b)the same L and different values of R,(c)plots of eigenfrequency versus point-contact position Rd for the same R and different values of L.

The eigenfrequency is a vital parameter of the MV application for nano-oscillators and modulators.We obtain the eigenfrequency of MV gyration from fast Fourier transform based on magnetizationThe dependence of eigenfrequency on the current density j and Rdis summarized in Fig.3.The eigenfrequency increases as the ratio of thickness to radius(L/R)increases as shown in Fig.3(a),which accords with the previous conclusion.[30]We also find that the dependence of eigenfrequency on the j is distinct in different disks.For the thin disk with L=15 nm,the eigenfrequency first increases with j increasing and it turns a constant with j further increasing,and the thinner disk has similar dependence of eigenfrequency on the j as demonstrated in our previous study.[22]However,the eigenfrequency first increases and then decreases with j further increasing,which is a peculiar dynamical phenomenon in thicker disks. Figure 3(b)illustrates the dependence of eigenfrequency on current density j in nanodisks with the same thickness. The eigenfrequency will increase with j increasing in these disks.By comparing the eigenfrequencies among different disks,we can also observe the prior confirmed relations between the L/R and the eigenfrequency.[30]To further explain how the point-contact position influences the eigenfrequency,we illustrate the eigenfrequency as a function of Rdin Fig.3(c),the MV eigenfrequency in thin disks decreases with Rdincreasing at a fixed j. However,for the MV in the thicker disks,it first increases with Rdincreasing and then decreases for the larger Rd.

The MV trajectory and velocity are other two important dynamic parameters of gyration.The trajectory is also different in thick and thin disk at Rd=0.1 as shown in Figs.4(a)and 4(b).The radius of MV steady orbit increases with j increasing in both the thicker disks and the thinner disks.However,it is obvious that the orbital radius in the thicker disks is much smaller.As shown in Figs.4(c)and 4(d),the MV velocity increases with j increasing.Moreover,there is another point worthy to be investigated.Namely,the velocity in thick disks is much lower than that in thin disks when the j values are the same. For example,when j is 10×1011A/m2,the average value of steady velocity is 210 m/s in the disk with 2R=400 nm and L=35 nm,while the average value can reach to 297 m/s in the disk with 2R=400 nm and L=15 nm.

Fig.4.Steady gyration orbits of magnetic vortex in(a)thick and(b)thin nanodisk.Steady gyration velocities of magnetic vortex in(c)thick and(d)thin nanodisk.

Besides the different orbit radii and steady velocities,another parameter should be paid more attention to,which is the excitation time and it is defined the time interval between the start of current injection and the MV reaching the steady gyration.We plot excitation time as a function of j and Rdin Fig.5.It is observed that the excitation time will decrease with j increasing in all nanodisks.Figure 5(a)shows that the excitation time of thicker nanodisks is greatly larger than that of thinner nanodisks.Furthermore,as observed.the point-contact position also has a great influence on the excitation time and the MV is the easiest to trigger when the point-contact Rdis between 0.2 and 0.4 as shown in Fig.5(b).Through the above analysis,we find that the MV has a larger eigenfrequency in the thicker and smaller nanodisk,but it needs the higher current density and longer time to trigger the MV to implement gyration.

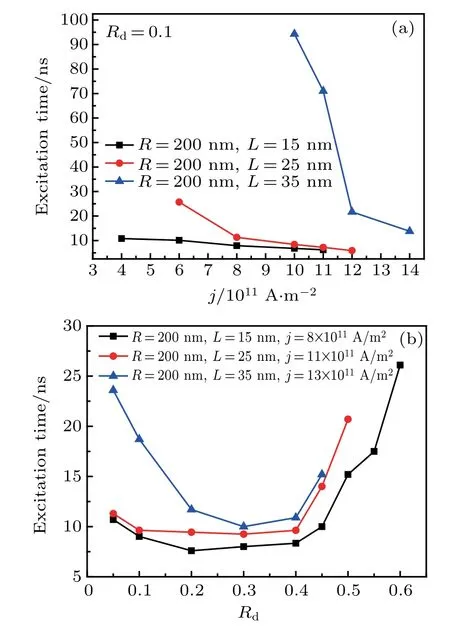
Fig.5.Plots of excitation time versus(a)j for Rd=0.1 and three different values of group of R and L,and(b)Rd for three different values of group of R,L,and j.

3.Conclusions

In this work,the gyration of the magnetic vortex in different permalloy nanodisks are analyzed,including the critical current density of triggering magnetic vortex gyration,eigenfrequency,trajectory,velocity,and excitation time. It is observed that the magnetic vortices in larger and thinner nanodisks can obtain gyration at a lower current density and shorter excitation time,whereas they have low eigenfrequencies. On the contrary,the magnetic vortices in thicker nanodisks need higher current density and longer time to attain steady gyration but have larger eigenfrequencies. Furthermore,the simulation results demonstrate that the point-contact position of spin-polarized current has great effects on these parameters and therefore,the magnetic vortex gyration can be controlled by the point-contact position.The calculation results and analyses in this work can open the way for designing magnetic vortex nano-oscillators and modulators.