Shan-Shan Yuwen(宇文珊珊),Lian-He Shao(邵連合),and Zheng-Jun Xi(席政軍),?College of Computer Science,Shaanxi Normal University,Xi’an 7006,China

2School of Computer Science,Xi’an Polytechnic University,Xi’an 710048,China

(Received May 5,2019;revised manuscript received June 18,2019)

AbstractWe find tight upper bound on the coherence of a superposition of two states in terms of the coherence of the two states constituting the superposition with l1-norm of coherence.Our upper bound is tighter than the one presented by Liu,et al.[Quantum Inf.Process.15(2016)4209.]We also generalize the results to the case that the superposition is constituted with more than two states in high dimension,and we give the corresponding upper bounds.

Key words:quantum coherence,superposition states,l1-norm of coherence

1 Introduction

Quantum coherence arises from quantum superposition,which plays a central role in applications of quantum physics and quantum information science,and also a common necessary condition for entanglement and other types of quantum correlations.Baumgratz,et al.proposed a theoretical framework for quantitative study of quantum coherence from the perspective of resource theory.[1]Based on this,various ways have been presented to develop the resource-theoretic framework for understanding quantum coherence,[2?11]we refer to two comprehensive reviews[12?13]for more discussions about resource theory of coherence.

Although there are many discussions on coherence measure for quantum states,there are few studies on superposition states that what is the relationship between the superposition state and the superimposed states.In the field of entanglement,Linden,et al. have firstly studied the relationship between the entanglement of a superposition state and its arbitrary decomposition in Ref.[14]. Shortly after,for the same question,Gour gave a tight upper bound and a new lower bound on the entanglement of a superposition of two bipartite states in terms of the entanglement of the two states constituting the superposition.[15]Thereafter,many interesting results have been obtained.[16?26]In quantum coherence theory,we are also interested in the relationship between the coherence of|?and that of|ψ1and|ψ2,where|?= α1|ψ1+ α2|ψ2with|α1|2+|α2|2=1.In particular,the states|ψ1and|ψ2are maximum coherent states on qubit system,the coherence of superposition|? is possible to zero.We can raise a problem:given a superposition state,what is the relation between the coherence of it and those of the components in the superposition? Liu,et al.discussed the bounds of coherence of superpositions with two components using l1-norm of coherence,where every component comes from the qubit system.[27]Using three different measures,Yue,et al.gave the upper and lower bounds for coherence of the superposition states of two states in terms of the coherence of the two states being superposed.[28]

In this paper we give a tight upper bound on the coherence of superposition states with two orthogonal states,which is tighter than the one presented in Ref.[27].We then generalize the ideas raised in Ref.[28]to the coherence of superpositions with more than two(n>2)components.We give the upper bounds using l1-norm of coherence.This paper is organized as follows.In Sec.2,we give the tight upper bound for the superposition of two states using l1-norm of coherence.We then give the upper bounds for the superposition of more than two states using l1-norm of coherence.We summarize our results and discuss further problems in Sec.3.

2 The Coherent Superposition of Pure

Coherent States

We introduce some concepts about coherence measure that can be used for our main results.[1,12]Given a ddimension Hilbert spacewith a fixed orthogonal basiswe denote the set of all density operators acting on H by D(H).The density operators which are diagonal in this fixed basis are called incoherent,we denote the set of all incoherent states byand.Any incoherent state δ is of the form

where δjare probability distribution.Any state which cannot be written as above form is defined as the coherent state,which means the coherence is basis-dependent.Baumgratz,et al.presented the axiomatic approach to quantify coherence in Ref.[1].Subsequently,several authors generalized this result to different measures of coherence,and many interesting results are given.In this paper,we focus on the l1-norm of coherence.For any quantum state ρ on H,the l1-norm of coherence[1]is defined as

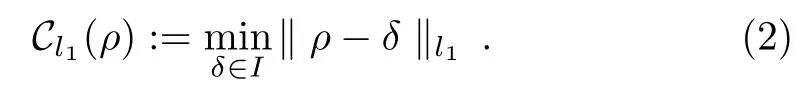
This quantifier has a more directly expression,[1]and

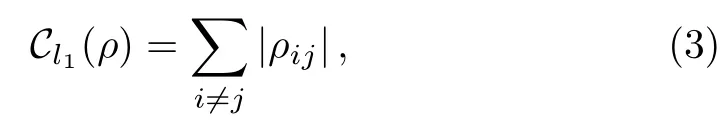
where ρijis the matrix elements of density operator ρ under the fixed basis{|j }.

We often say that a unit vectoris a pure state oris a pure state,and we use ψ to denote pure statein D(H).For any pure stateone can easily check[4,29?30]

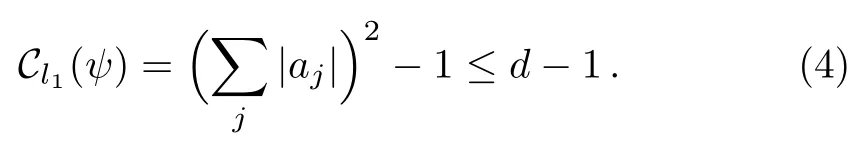
In this paper,we are interested in the relation between the coherence of a superposition state and the coherence of the individual states in the superposition.Without of loss generality,we suppose that

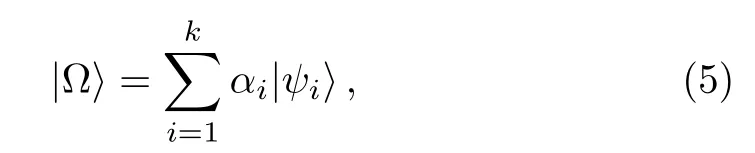
where 2≤k≤d,and∑i|αi|2=1.Here,the statesare coherence states with the fixed basis{|j },and

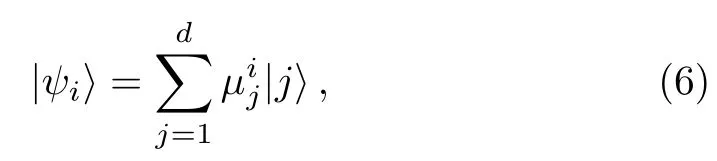
2.1 The Superposition with Qubit System

Firstly,we consider the superposition state constituted with two individual states in qubit system.

Proposition 1 Given a state

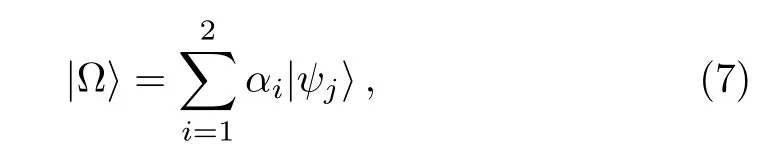
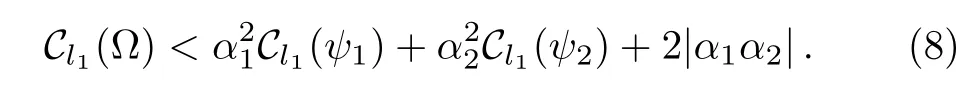
Proof Let us consider the states:

From Eq.(4),we have

Then we will have

Thus,we have

Since a1is a real number and can not be 0 and 1,we have|1?<1.Then we can get our upper bound

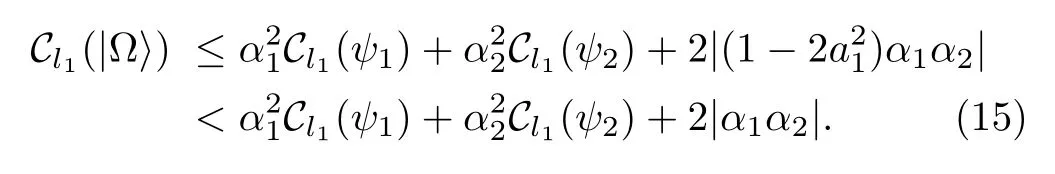
The coefficient|α1α2|can be considered as the relative coherence,because we find that the|α1α2|is only relative to the statesand,from Eq.(15)we can see that the coherence ofis also related to the internal coherence of the statesand.And for the same question in Ref.[27],the authors did not consider the nature of orthogonality,that is why our upper bound is tighter than the one they presented.Now we consider two examples.

Example 1 Consider the states

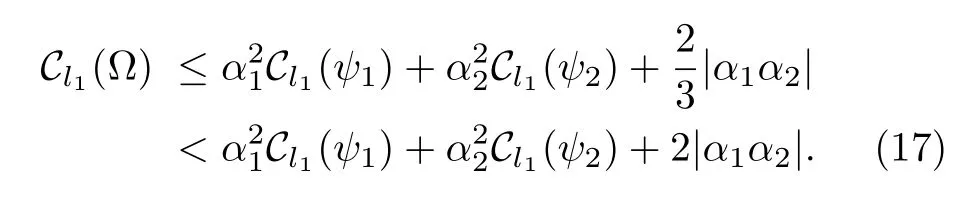
Example 2Consider the states

It is clearly that Cl1(ψ1)=Cl1(ψ2)=1.The coherence of the superposition|? satisfies

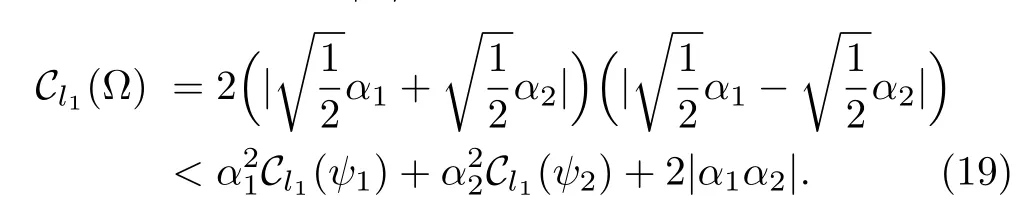
From Proposition 1,we can easily get the maximum increase of the coherence of superposition states.

Corollary 1Given states|ψ1and|ψ2orthogonal,the maximum increase of coherence satisfies

From the Example 1,we can see that the increase of the coherence ofis(2/3)|α1α2|.And this is for the superposition of orthogonal states.Now we consider the general case,which means the two superimposed states are non-orthogonal,we can also get an upper bound.We believe that the upper bound of the coherence of the superposition states with two non-orthogonal states is consistent with the upper bound of the coherence of the superposition states with two orthogonal states proposed by Liu,et al.[27]

Proposition 2Given a statewhereand bjare real numbers and satisfy.The coherence of the superpositionsatisfies

From Proposition 2,we can easily get the maximum increase of the coherence of superposition states.

Corollary 2Given arbitrary statesand,the maximum increase of coherence satisfies

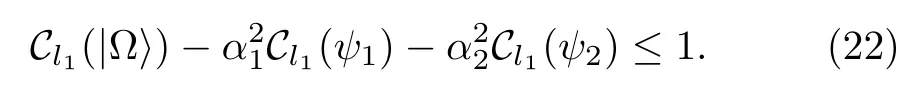
2.2 The Superposition with more than Two States

The above upper bounds are for the states with qubit system.Yue,et al.proposed upper and lower bounds for coherence of the superposition with two states in ddimensional system.We now present the upper bound for the superposition of more than two states using l1-norm of coherence.

Proposition 3Given a state,whereare orthogonal, αiare real numbers and satisfyThe coherence of the superpositionsatisfies

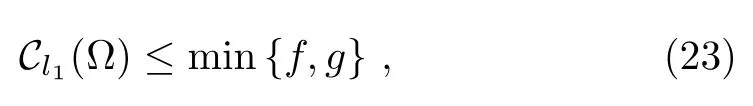
where

ProofWithout loss of generality,let

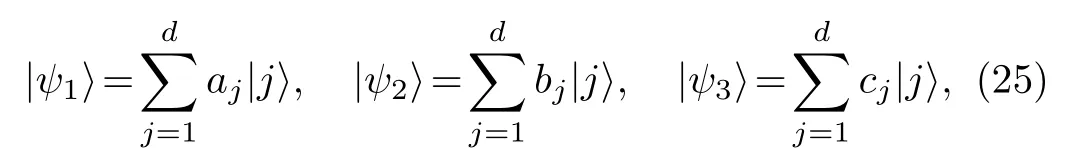
where aj,bj,and cjare complex numbers and satisfyFor superposition state,we have

where the first inequality comes from the absolute value inequality,the second inequality comes from successive appli-cation of the mean inequality.

Next we will prove the second upper bound in Eq.(23).Using the relation(4),we have

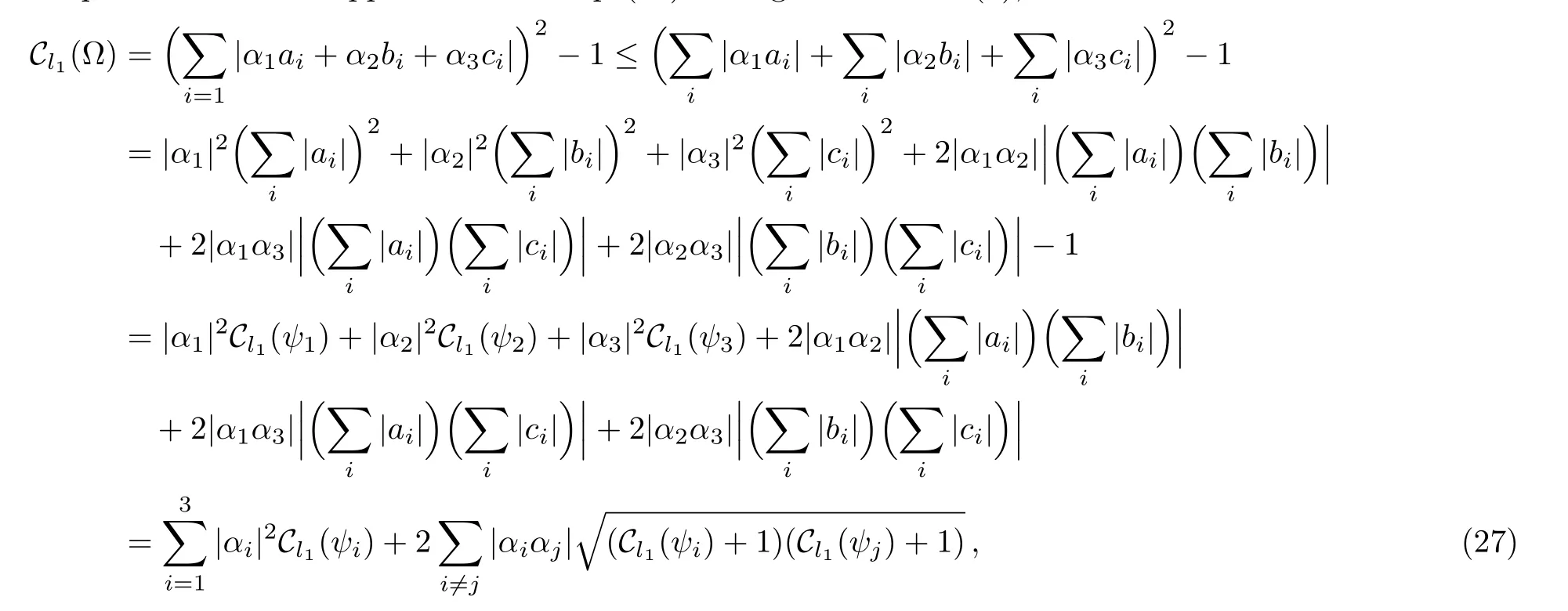
where the inequality is due to the absolute value inequality.

Note that the relationship between the coherence of two orthogonal states and the coherence of their combination using l1-norm of coherence is given in Ref.[28].Our result focuses on the coherence of superpositions with more than two components,and our result can also be generalized to the state which is superposed by n orthogonal states.

Corollary 3Given statesmutually orthogonal,the upper bound of coherence of the superposition state1 is given as

where

Remark 1

(i)It is obviously that our results can be reduced from n components to two components.

(ii)We find that for the general states,while satisfyingthe larger the value of α1,the smaller the values of α2and α3,the tighter the upper bound we get.For example,we suppose that α1=we have

where

(iii)For the maximum coherent state,this upper bound only makes sense in special cases.We suppose thatare maximum coherent states,with Proposition 3,we have

For the special case that α1→ 1,α2,α3→ 0,we can get a meaningful upper bound Cl1(?)≤ d?1,but for another√special case that α1= α2= α3=1/we get a meaningless upper bound Cl1(?)≤ {3(d?1),3d?1}.

We find that in Ref.[28],the same problem also exists.Whenare maximum coherent states,α1= α2=1/the upper bound we get is

The reason for this is the shrinking of in equations in Eqs.(26)and(27),and we do not have better solutions now.

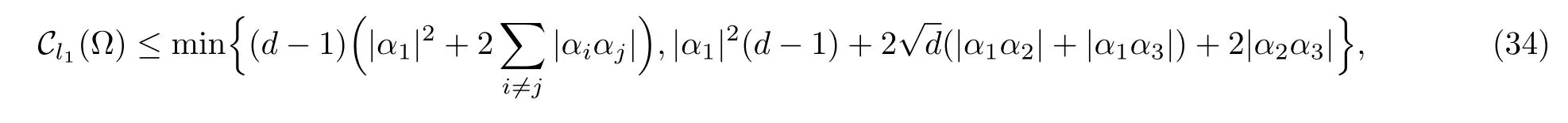
when α1→ 1,α2,α3→ 0,we have Cl1(?)≤ |α1|2(d? 1).

3 Conclusion

In this paper,we have presented a tighter upper bound on the coherence of a superposition of two states in terms of the coherence of the two states constituting the superposition with l1-norm of coherence.We have established the relationship between the coherence of the superposition of three states and the coherence of the three states constituting the superposition with l1-norm of coherence.We also generalized the result of the superposition of three states to the superposition of n states.In the calculation we found that it is more difficult for the superposition of more than two states.The bounds we get is not very tight in some cases.For the future work we hope to find new methods to make the upper bounds we get more tighter.