Analysis of radial stiffness of rubber bush used in dynamic vibration absorber
Li Lie Sun Beibei Hua Haitao
(School of Mechanical Engineering, Southeast University, Nanjing 210096, China)
Abstract:In order to study the influence of the structural parameters of the rubber bush on its radial stiffness, the constitutive relation of rubber materiel is used to obtain the calculation formula of the dimensionless radial stiffness coefficient. The obtained theoretical result is consistent with previous research results in both long rubber bushes and short rubber bushes. The simulation case was conducted by the finite element method to verify the correctness of the theory. The axial compression experiment was conducted to obtain the parameters needed in the simulation. The result shows that the percentage difference between the theoretical result and the simulation one is only 2.75%. A series of simulations were conducted to compare with previous work, and the largest magnitude of the percentage difference is only about 5%. Finally, the radial stiffness experiment was conducted by using a dynamic vibration absorber, and the influence of the structural parameters of the rubber bush on its radial stiffness is obtained. The result shows that the radial stiffness of the rubber bush increases with the increase in the length and the inner radius, but decreases with the increase in the outer radius.
Key words:radial stiffness; rubber bush; dynamic vibration absorber; boring bar
The rubber bush is widely used in many mechanical products working as a kind of spring for vibration isolation or comfort requirements[1]. Its main function is to join the rigid structures. In most cases, the axial stiffness of the rubber bush is the focus, but in some special cases, the radial stiffness needs to be considered[2-4]. Due to the increasing interest of multibody simulations, it is important to develop models to represent the static stiffness of these rubber products[5]. Many scholars have tried to study the radial stiffness of the rubber bush. However, due to the complicated rubber material, geometry and contact, this problem has not been effectively solved[6-8]. Stevenson[9]studied the boundary problem of two-dimensional elastic materials, established the boundary equation, and obtained the dimensionless calculation formula for radial stiffness. Adkins et al.[10]studied the radial stiffness of rubber bushes with different sizes based on the classical linear elastic theory. The reduced radial stiffness,βLandβS, of long and short bushes with inner and outer radiiAandBare given by
(1)
(2)
Horton et al.[11-12]obtained an exact expression of the radial stiffness of the rubber bush and derived a convenient approximation. The calculation results were compared with the experimental data in Ref.[10]. Hill[13]obtained an exact expression for small radial deformations of the bonded cylindrical rubber bush of finite length by using the truncated Fourier and Fourier-Bessel series. Qin et al.[14]established a finite element model and obtained the relationship between the radial stiffness and the parameters of the rubber bush. Li et al.[15]conducted a two-dimensional finite element simulation of the rubber bush and the axial compression of the rubber bush was studied to discover its effect on radial stiffness. The result shows that when the axial compression increases, the radial stiffness increases nonlinearly. In existing research, the rubber bush is usually considered to be of finite length, resulting in a certain limitation of the theoretical formula. In addition, the existing research lacks necessary simulations and experimental verification. In this paper, the constitutive relation of rubber materiel is used to conduct a theoretical analysis to obtain a more general reduced radial stiffnessβ. The theoretical result is consistent with previous research results in both long rubber bushes and short rubber bushes. Then, the simulation and experiment are conducted, and the results show that the errors between the theoretical result, the simulation result and the experiment result are very small, which provides a calculation approach to meet target radial stiffness.
1 Theoretical Method
Fig.1 shows the structure of the damping boring bar equipped with a passive dynamic vibration absorber(DVA) consisting of mass block damping oil and a rubber bush. The mandrel is fixed with the bar. When the bar vibrates, the vibration energy will transfer from the mandrel to the mass block through the rubber bush. Then, the vibration energy will be consumed due to the vibration absorbing effect of the damping oil.
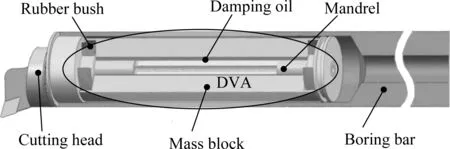
Fig.1 The structure of the DVA used in a damping boring bar
In order to obtain a better vibration absorption effect, the DVA needs to resonate when vibration occurs. Therefore, the natural frequency of the DVA needs to be designed to match the natural frequency of the bar. As the radial stiffness of the rubber bush has a direct influence on the natural frequency of the DVA, in order to resonate with the DVA, the radial stiffness of the rubber bush needs to be designed.
In order to study the radial stiffness, the rubber bushes used in DVA can be modeled as shown in Fig.2. The rubber bush is placed between the inner and outer metallic hollow cylinders.A,BandLare the inner radius, outer radius and the length of the rubber bush, respectively.

Fig.2 The structural model of the rubber bush
We create a coordinate system as shown in Fig.3. Let the coordinates of a point in the rubber bush in the Cartesian coordinate be (x,y,z), while in the polar coordinate be (r,θ,z). The relationship between the two coordinates is
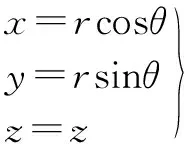
(3)
The radial, tangential and axial components of the displacement of the pointPare denoted byu,v,w, respectively. Then, the radial, tangential and axial normal strain components are, respectively, given by
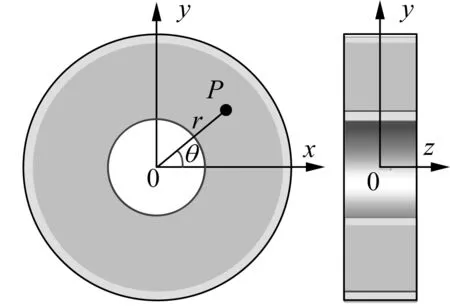
Fig.3 The calculation model of the rubber bush
(4)
and the shear strain components are
(5)
Assuming that the rubber material is isotropic, the constitutive equation of stress and strain are
(6)
and
(7)
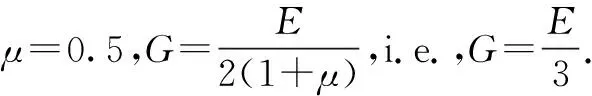
σrr=σzz+2G(2εrr+εθθ),σθθ=σzz+2G(εrr+2εθθ)
(8)
By considering the equilibrium in the direction of thez-axis, the following equation of equilibrium must be fulfilled:
(9)
Suppose that the inner cylinder is fixed and the outer cylinder is loaded by a forceFacting in the direction of the positivey-axis to create a displacementd. The main object is to find the expression of the stiffness,F/d. The displacementdcan be obtained by the superposition of the displacement created in two separate situations. In the first situation, the rubber bush is subjected not only to the loadFbut a specific axial stress inzdirection to prevent the plane ends from distorting. An expression can be found for the radial displacement,d1, of the outer cylinder. In the second situation, the plane ends are subjected to loads equal and opposite to those in the first situation. An expression can be found for the radial displacement,d2, of the outer cylinder. Then,d=d1+d2can be obtained.
In the first situation, suppose that the plane ends are subjected to an stressσzz=W(r), then the corresponding displacement components at pointPare
u=U(r)sinθ,v=V(r)cosθ,w=0
(10)
It follows from Eq.s (4) and (5) that the non-zero strain components are given by
(11)
For small strains, the assumption of incompressibility implies that
εrr+εθθ+εzz=0
(12)
Then
(13)
And Eqs. (7), (8) and (11) yield
(14)
For the first situation, Eq.(9) thus reduces to
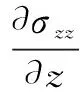
(15)
Considering a cylindrical surface of radiusralong thez-axis, we have
(16)
Evaluating this by substitutingσzz=Wsinθinto Eq. (14), then
(17)
Stevenson[9]once pointed out that
(18)
UandVcan be obtained by substituting Eq.(18) into Eq.(17).
(19)
The outer cylinder does not move in thexdirection, soU(B)=V(B)=d1. Then, we have
(20)
In the second situation, by using the same method as above, we have
(21)
(22)
The radial stiffness calculation formula of the rubber bush can be obtained.
(23)
This leads to a non-dimensional representation of the reduced radial stiffnessβin the form
(24)
Compared with the results of Adkins et al.[10]shown in Eqs.(1) and (2), it can be seen that
β→βL,L→∞
(25)
AsL→0,
(26)
Hence,
(27)
It means asL→0,βis extremely close toβs.
2 Simulation of the Radial Stiffness of Rubber Bush
2.1 Case study
A simulation case by using the finite element method is carried out to verify the correctness of the theory. The most important of the finite element method is to establish an accurate model and obtain the accurate parameters of the rubber bush. In order to obtain the parameters of the rubber bush required in the simulation, the axial compression experiment is conducted, as shown in Fig.4.

Fig.4 The axial compression experiment of the rubber bush
The axial stiffness for a rubber bush is
(28)
whereD,dandhare the outer diameter, inner diameter and length of the rubber bush.Eais apparent Young’s modulus.
Ea=iG
(29)
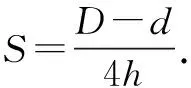
(30)
Fig.5 shows the force-displacement curve of the axial compression experiment. By deriving, the radial stiffness of the rubber bush can be obtained aska=120 N/mm. In this case,D=24.2 mm,d=11.5 mm,h=7.1 mm, and thenG=0.5 MPa,E=3G=1.5 MPa.
The three-dimensional simulation model is established in the finite element software Abaqus as shown in Fig.6. The inner and outer cylinders are set as a rigid body, while the rubber bush is set as an elastic body.
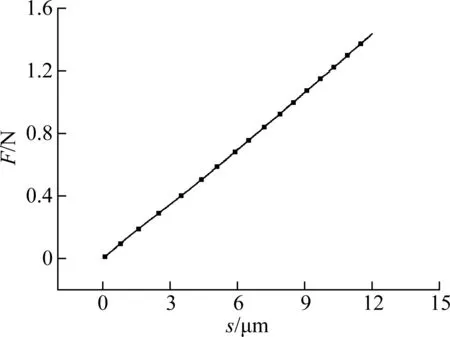
Fig.5 The force-displacement curve of the axial compression experiment
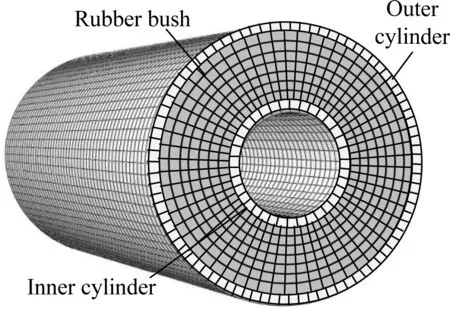
Fig.6 The finite element model of the rubber bush
As shown in Fig.7, the inner cylinder is fixed and the outer cylinder is loaded by forceF, which will lead to a displacementd. The main objective here is to find the value of the stiffnessK=F/d.
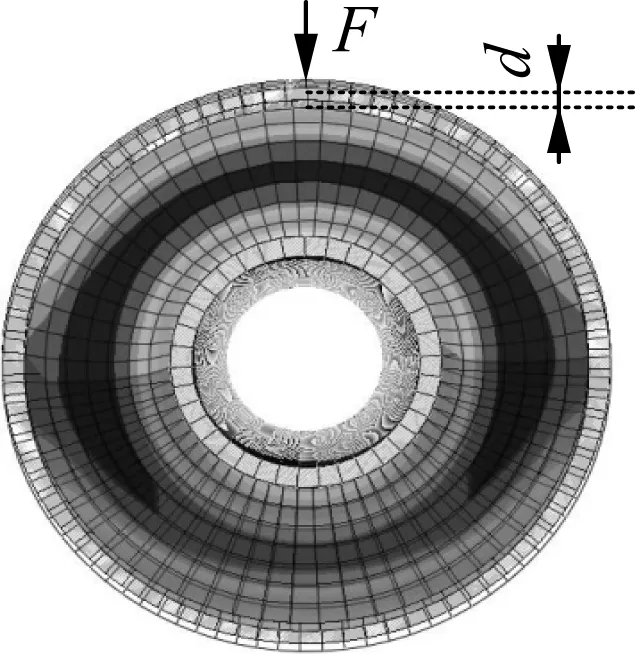
Fig.7 Calculation model
Define material properties as the calculated results above. Using reduced-integration hybridization elements, a total of 22 357 elements are obtained. By loading the out cylinder and fixing the inner cylinder, the radial displacement of the rubber bush can be obtained, and then the radial stiffness calculated through simulations can be obtained as 67.14 N/mm. Compared to the theoretical result 69.04 N/mm, the percentage difference is only 2.75%.
2.2 Contrast with previous work
A series of simulations were conducted to compare with previous work. The simulation parameters selected were the same as those in Ref.[10]. Tab.1 shows the results. The seventh column gives the experimental values obtained by Adkins et al.[10], and the simulation values are listed in the sixth column. It can be seen that the experimental values are very close to the simulation values, but slightly lower than them. This is because, in the simulation, the inner and outer cylinders were set as rigid bodies, which means that they will never be deformed. However, in the experiment, the cylinders were made of compressible metal. The metal cylinders and the rubber bushes were deformed at the same time. Larger deformation leads to lower radial stiffness in the simulation. However, it is interesting to note that the largest magnitude of the percentage difference, listed in the eighth column, is only about 5%.
Tab.1Radial stiffness of the rubber bush with different parameters
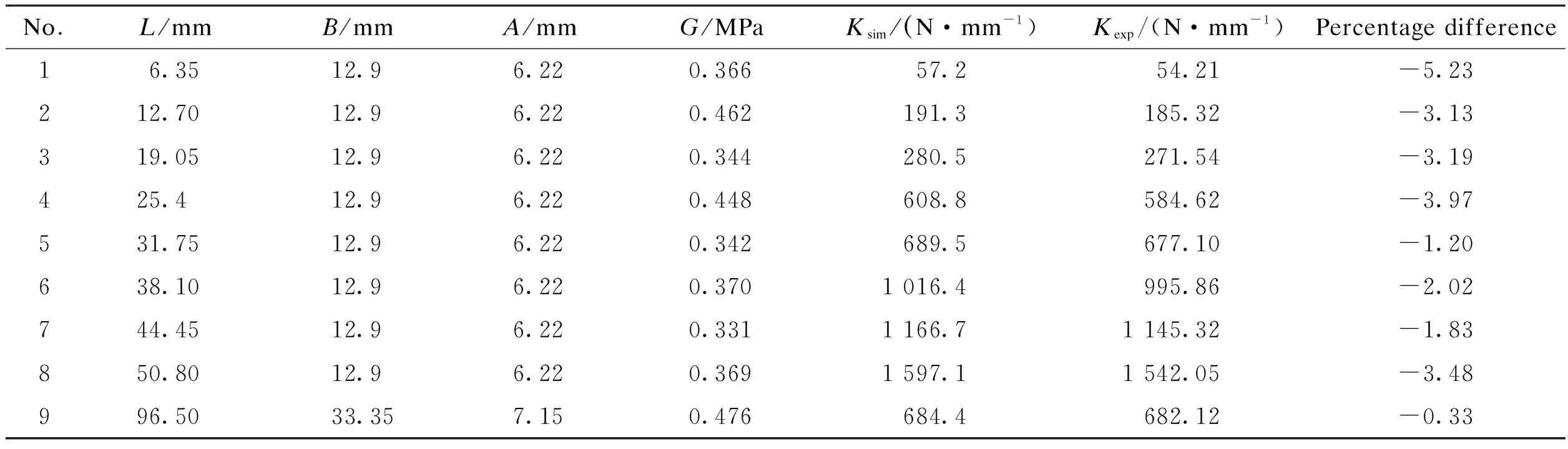
No L mmB mmA mmG MPaKsim N·mm-1)Kexp/(N·mm-1)Percentage difference16.3512.96.220.36657.254.21-5.23 212.7012.96.220.462191.3185.32-3.13 319.0512.96.220.344280.5271.54-3.19 425.412.96.220.448608.8584.62-3.97 531.7512.96.220.342689.5677.10-1.20 638.1012.96.220.3701 016.4995.86-2.02 744.4512.96.220.3311 166.71 145.32-1.83 850.8012.96.220.3691 597.11 542.05-3.48 996.5033.357.150.476684.4682.12-0.33
3 Experiment of the Radial Stiffness of Rubber Bush
The experiments of the radial stiffness with different sizes were carried out to study the effect of sizes on radial stiffness. The experiments were carried out on the pressure test platform as shown in Fig.8. The DVA is applied with a radial displacement. The cut-off force is set to be 120 N and the loading speed is controlled at 1 mm every 5 min. The low cut-off force and slow control speed ensure that the rubber bush can always work in a linear condition without hysteresis effects. The sensor can record the force and displacement data in real time. Then, the radial stiffness can be calculated through the force-displacement curve. It can be seen from Eq.(23) that when the shear modulus is constant, the radial stiffness is influenced only by the outer radius, inner radius and length of the rubber bush. The case withD=24.2mm,d=11.5mm,h=7.1 mm is set as a reference.
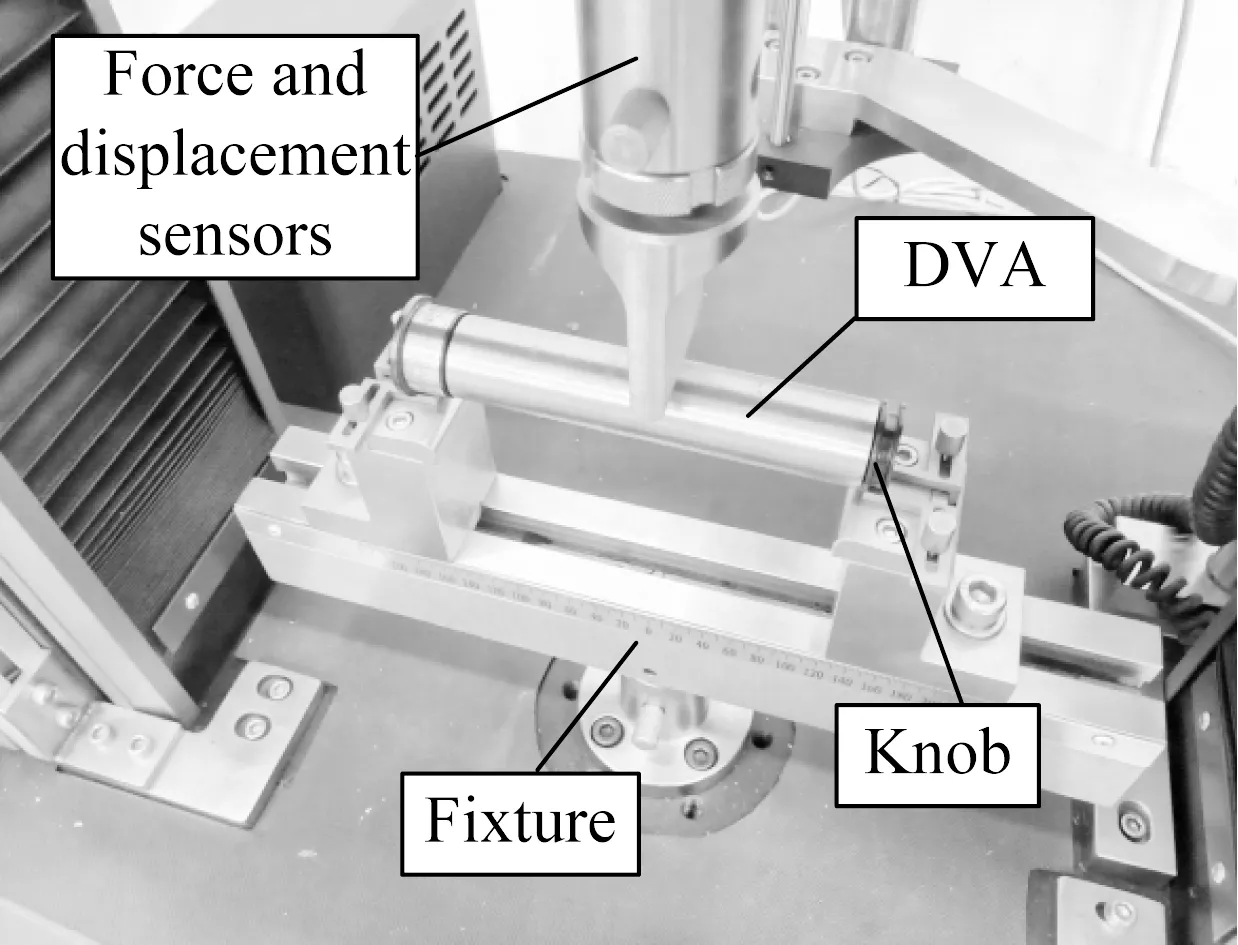
Fig.8 The experiment of radial stiffness under different sizes
It is worth noting that there are two rubber bushes placed parallel in a DVA(see Fig.1). The radial stiffness of each rubber bush can be calculated by
(31)
Fig.9 shows the effect of the length of the rubber bush on its radial stiffness. It can be seen that the radial stiffness increases linearly with the increase in length. This is because the radial stiffness per unit length is constant, so when the length of the rubber bush increases, it is equivalent to the parallel connection of a plurality of springs. Fig.10 shows the influence of the inner radius of the rubber bush on its radial stiffness. It can be seen that the radial stiffness increases nonlinearly with the increase in inner radius. That is because, with the increase in inner radius, the thickness of the rubber bush decreases. Therefore, under the same applied force, the displacement decreases, resulting in a greater radial stiffness. Fig.11 shows the effect of the outer radius of the rubber bush on its radial stiffness. It can be seen that the radial stiffness decreases nonlinearly with the increase in outer radius. This is because, with the increase in outer radius, the thickness increases, and it is equivalent to the series connection of a plurality of springs. It is worth noting that the errors between the theoretical curve, the simulation curve and the experimental curve are very small. This further validates the accuracy of the previous theory and simulation study.
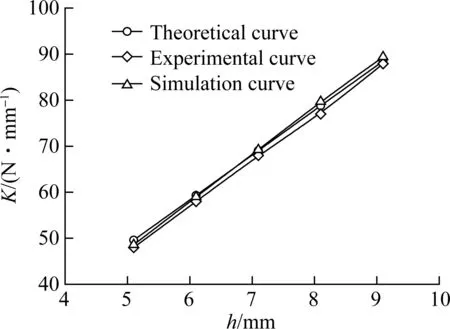
Fig.9 Effect of the length of the rubber bush on its radial stiffness
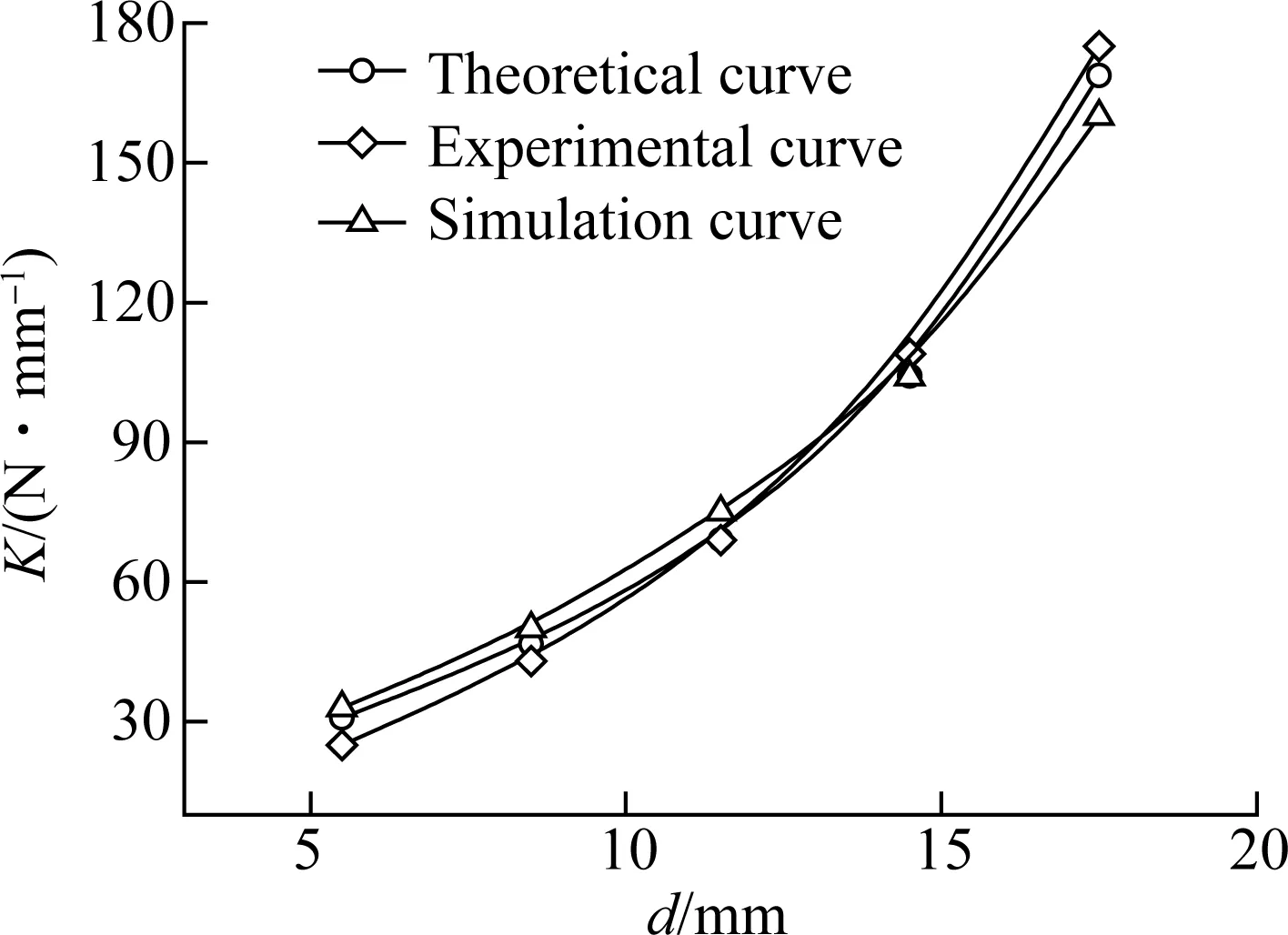
Fig.10 Effect of the inner radius of the rubber bush on its radial stiffness
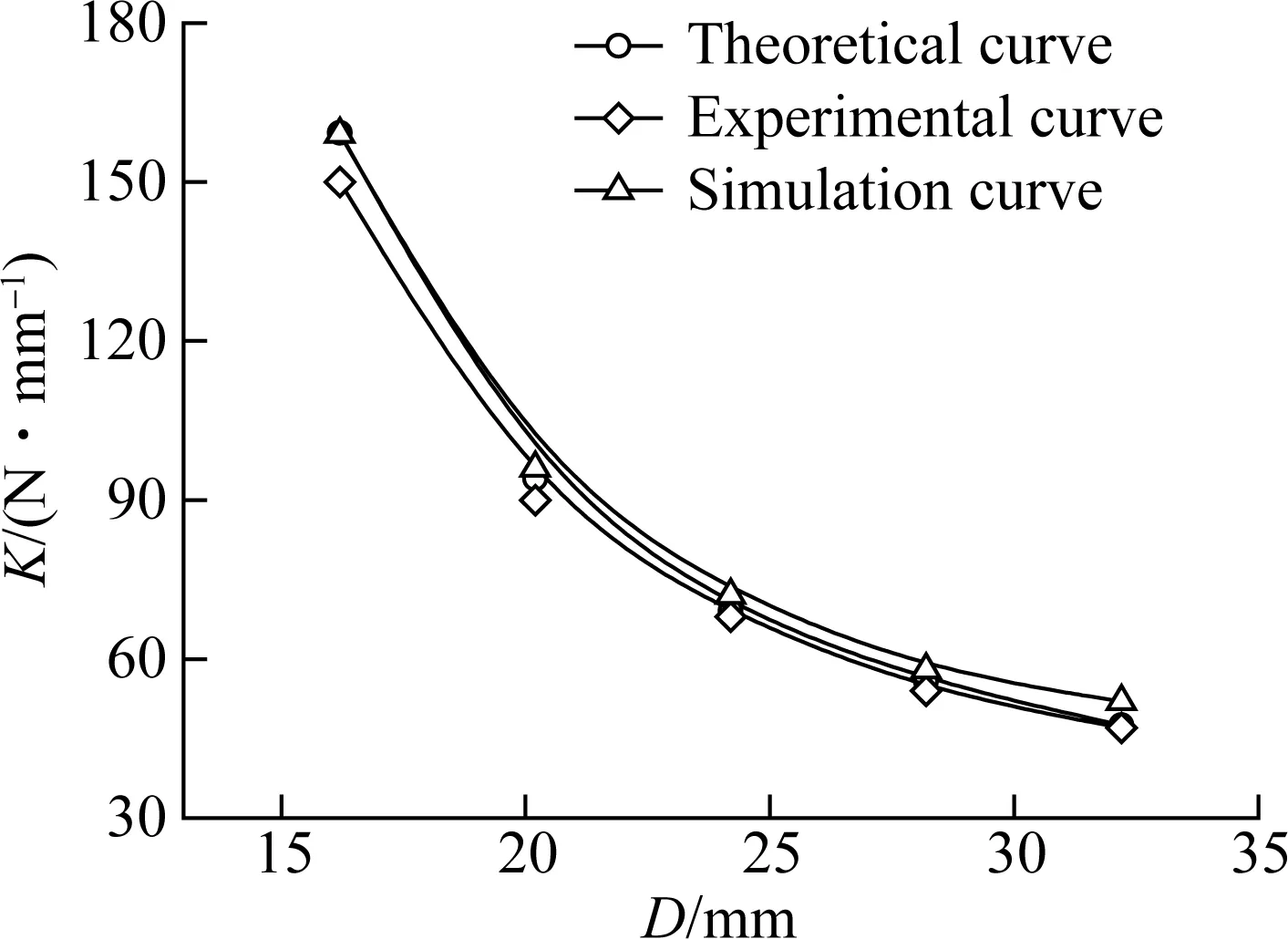
Fig.11 Effect of the outer radius of the rubber bush on its radial stiffness
4 Conclusions
1) The radial stiffness of a rubber bush has a significant effect on the natural frequency of DVA. The constitutive relation of rubber material is used to conduct a theoretical analysis, and reduced radial stiffnessβis obtained. The calculation formula obtained is consistent with previous research results in both long rubber bushes and short rubber bushes.
2) The simulation case by using the finite element method is used to verify the accuracy of the theory. In order to obtain the parameters required in simulations, the axial compression experiment is conducted. The result shows that the percentage difference between the theoretical result and the simulation result is only 2.75%.
3) A series of simulations were conducted to be compared with previous work. The results show that the simulation values are very close to the previous experiment values, but slightly lower than them. However, it is interesting to note that the largest magnitude of the percentage difference is only about 5%.
4) An experiment is conducted to verify the accuracy of the theory and simulation. The results show that the radial stiffness increases linearly with the increase in length, increases nonlinearly with the increase in inner radius and decreases nonlinearly with the increase in outer radius. In addition, the errors between the theoretical curve, the simulation curve and the experimental curve are very small. This further confirms the accuracy of the previous theory and simulation study.
 Journal of Southeast University(English Edition)2019年3期
Journal of Southeast University(English Edition)2019年3期
- Journal of Southeast University(English Edition)的其它文章
- Experimental investigation of oil particles filtration on carbon nanotubes composite filter
- Projection pursuit model of vehicle emission on air pollution at intersections based on the improved bat algorithm
- Effect of waste concrete with different strengthon mechanical properties of recycled fine aggregate mortar
- Tensile behaviors of ecological high ductility cementitious composites exposed to interactive freeze-thaw-carbonation and single carbonation
- Travel time prediction model of freewaybased on gradient boosting decision tree
- Image denoising method with tree-structured group sparse modeling of wavelet coefficients
