Nauman Raza and Asad Zubair

Department of Mathematics,University of the Punjab,Quaid-e-Azam Campus,Lahore,Pakistan

AbstractThe ultimate theme of this study is to develop dipole and combo optical solitons in birefringent fi bers(BF)along with the effect of four-wave mixing(4WM).Two types of rough mediums are used which are Kerr law and parabolic law.Ansatz method of Choudhuri is applied to obtain dark in the bright(dipole)soliton solutions providing bright background for the propagation of optical dark pulse.Ansatz method of Li is applied to obtain combo soliton solutions providing bright solitary wave and dark solitary wave solutions.These results also exist to hold in non-Kerr media with higher order dispersion.

Key words:dipole solitons,combo solitons,ansatz methods,four-wave mixing,birefringent fi bers

1 Introduction

For a long time,optical solitons,peculiar waves that can narrate for long intervals without distortion,were just contemplated as a hypothetical perception.In 1980,existence of solitary waves in optical fi bers were first experimentally manifested by Mollenauer et al.[1]They verified the hypothetical work,that optical soliton is the effect of an intricate balance between dispersion and nonlinearity,build by Hasegawa and Tappert.[2]After this,a number of articles and several exertions have been devoted to investigate optical solitons in many areas of optical waveguides such as birefringent fi bers,semiconductors,optical crystals,DWDM,photonic crystals,optical couplers and so on.[3?12]

Nowadays a great deal of interest have been given to the study of interaction between dispersive waves(DWs)and solitons in optical waveguides.These types of phenomena frequently arises in the,designing of broadband sources,process of supercontinuum generation[13]and optical switching.[14]The fact of birefringence in an optical waveguide is unavoidable.This phenomenon steers to differential group delay via breaking of pulses into two.The collective response of this delay signi fi es birefringence.

In optical modes,refractive indices induced by orthogonally polarized components are slightly different in the case of fi ber birefringence.Nonlinear phenomena a ffected considerably through this refractive index,which plays an important role in the field of fi ber optics.Its effects should be included if Bragg gratings are made inside the core of polarization-maintaining fi bers.In order to account for fi ber birefringence it is worthy to extend the coupled-mode theory.[15?17]In this extent the evolution of two orthogonally polarized components are described through a set of four coupled equations containing forward and backward propagating waves which makes the problem quite complicated.This rami fi cation provides a major class of nonlinear phenomena with practical application,such as optical logic gates.

From a physical standpoint,there is a slight difference between the mode indices induced by two orthogonally polarized components.Since the Bragg wavelength relies upon mode index,the widths of the stop bands is same for the two modes but altered by a small amount with respect to each other.As a result,one of the polarization component falls inside the stop band while the other polarization component remains outside the stop band,despite the fact that both polarization components have a similar wavelength.Moreover,as the two stop bands shift due to nonlinear index changes,the shift can be different for the two orthogonally polarized components because of the combination of the cross-phase modulation(XPM)and birefringence effects.It is this feature that leads to a variety of interesting nonlinear effects.

Interaction of solitons/DW can take place in two different ways:the first one is non-phase sensitive[18]and the second one is phase sensitive.[19]In non-phase sensitive,soliton itself provokes moving refractive index variation,which is capable of generating new spectral bands via XPM.In this type band frequencies are explicitly independent of soliton phase.In phase sensitive new spectral bands are generated by using the four-wave mixing(4WM)process between DW and soliton.[20?24]In this type band frequencies depend on the soliton phase.Many mathematical problems for birefringence are fetched out in the absence of 4WM effect.However,some results are expressed with 4WM effect.[22?32]

The aim of this work is to develop dipole and combo soliton solutions in BF along with the 4WM effect and spatio-temporal dispersion(STD)for Kerr law and parabolic law nonlinearities.We choose a complex ansatz introduced by Choudhuri in Ref.[33]to extract dark-inthe-bright(dipole)soliton solutions and for combo soliton solutions we choose complex ansatz given by Li in Ref.[34].

Next our target is to find the soliton solutions.In Sec.2 we will find soliton solutions for Kerr law.In Sec.3 soliton solutions are presented for parabolic law which will be followed by some concluding remarks in Sec.4.

2 Kerr Law

Kerr effect is the nonlinear response of the medium to counter the nonlinear polarization generated in the medium due to the propagation of intense beam of light through the medium.The propagation of solitons in BF with 4WM and STD for Kerr law is described by the following vector generalized nonlinear Schr?dinger equation(v-GNLSE)[32]

In Eqs.(1)and(2),independent variables z and ? are spatial and temporal components respectively.The complex valued functions ?(z,?)and ψ(z,?)represent the solitary wave profiles for birefringent fi bers.First term in Eqs.(1)and(2)is the time evolution of pulses.For i=1,2,the coefficients of ai,bi,αi,βiand σiare group velocity dispersion(GVD),STD,self-phase modulation(SPM),(XPM)and 4WM respectively.While λiand μiare proportional to inverse group velocity difference and difference between propagation constants respectively.

In order to find soliton solutions of Eqs.(1)and(2),we introduce following traveling wave assumptions.[35?36]

where U1and U2are complex Envelope functions and r(z,?)= ?κz+ ω? + θ,is the linear phase shift.Here θ, ω,and κ are phase constant,wave number and wave frequency,respectively.

Substituting above transformation in Eqs.(1)and(2),we get

2.1 Dark-in-the-Bright Soliton

In order to find dark-in-the-bright(dipole)soliton solution we will choose following solitary wave complex ansatz for Eq.(5)

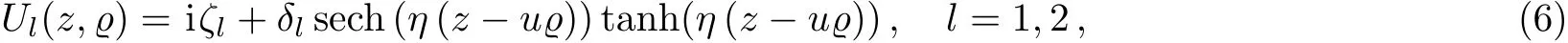
where u and η denote the shift of inverse group velocity and pulse width,respectively.[33]Moreover,the amplitude and the nonlinear phase shift rNLof complex envelop function in Eq.(6)is as follows

Substituting Eq.(6)into Eq.(5)and separating its imaginary and real components.Now collecting the coefficients of same powers of secmh×tannh,(m,n=0,1,2,3)and equating these coefficients equal to zero,provides a set of algebraic equations

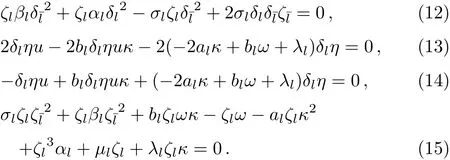
Now we have to impose some conditions on the above system(9)–(15)in order to find solitary wave solutions,there would be two cases ζl=0 and δl=0 or ζl=0 and δl=0.In case δl=0,we cannot reach to our desired results.The inclusion of the parameter ζlin Eq.(6)provides a non-zero background for the solitry wave when the time variable tends to infinity.For ζl=0,solving above system(9)–(15),we get

Under subsequent parametric conditions

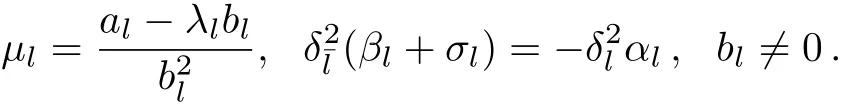
Equations(16)and(17)give the velocity and wave number of solitons respectively enforcing the following constraint conditions.

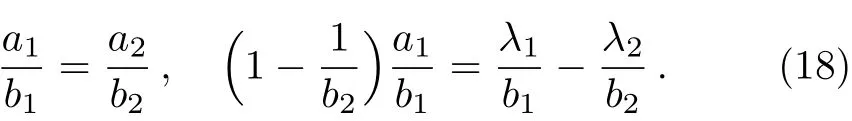
Now the exact dipole soliton solution in BF with Kerr law nonlinearity,depending upon above mentioned conditions is

The above solitary wave can be perceived as the coalition of bright and dark solitary wave.This solution shows the propagation of optical dark pulse with finite bright background width.This type of soliton is called dipole or dark in the bright soliton.[37]

Remark 1By taking some appropriate calculations,the obtained solution in this section will meet to the solution in Ref.[38]for αl=0.

2.2 Extraction of Combo Solitons

In order to extract bright-dark combo soliton solutions,we first present the subsequent ansatz

where ζl,for l=1,2 denote the grayness of solitons,while the coefficients ρland δl,for l=1,2,denote the amplitude of 1-bright and 1-dark solitons respectively.Ultimately,u and η are the velocity and width of solitons respectively.

The intensity of Eq.(21)is given as

and its corresponding nonlinear phase shift gives

Substituting Eq.(21)into Eq.(5)and splitting its real and imaginary components provides polynomials in linearly independent functions secmh×tannh,(m,n=0,1,2,3)whose coefficients equal to zero gives a set of algebraic equations. Again,there arise two cases δl=0 and ζl,ρl=0 or ζl=0 and δl,ρl=0.For the case δl=0,solving obtained set of algebraic equations gives Under subsequent parametric conditions

Equations(24)and(25)give the velocity and wave frequency of solitons respectively enforcing the following constraint conditions.

Now based on above parametric conditions bright soliton solution in BF with Kerr law nonlinearity can be written as

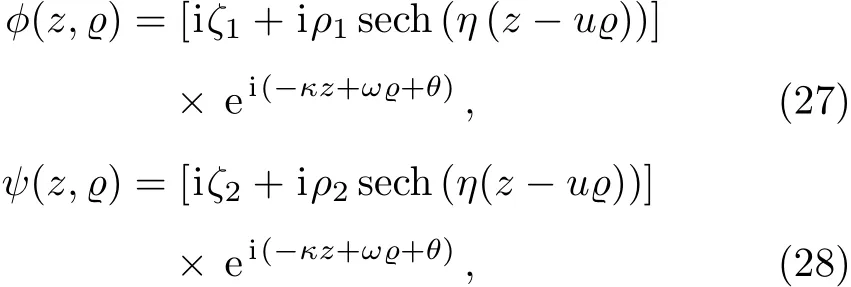
the band width of the solution given above is related to

Now for ζl=0 and again solving the obtained system of equations we obtain subsequent parametric values

In the above values u and ω give the velocity and wave number of solitons respectively enforcing the following constraint conditions

Now based on above parametric conditions we obtain subsequent combo soliton solution in BF with Kerr law nonlinearity

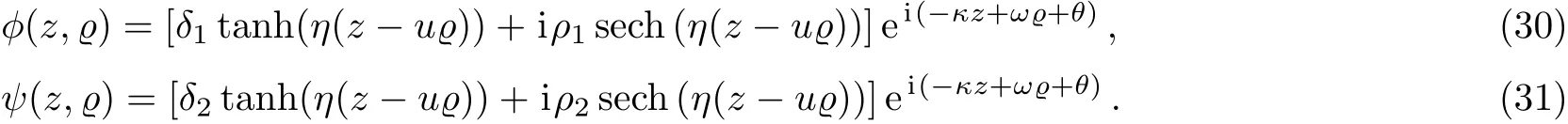
The solitary wave solution obtained above is the combination of 1-bright and 1-dark solitons with their corresponding amplitudes.If δl=0 and ρl=0 our above solution tends to bright solitary wave solution and if δl=0 and ρl=0 our above solution tends to dark solitary wave solution.When δl=0 and ρl=0 the above mentioned solution is called combo soliton solution.[37]

Remark 2In the case ζl=0,by taking some appropriate calculations,the obtained solution in this section will meet to the solution in Ref.[39]for σl=0 and for the case δl=0 the obtained solution in this section are new and reported for the first time.

3 Parabolic Law

The parabolic law nonlinearity effect is encountered when intense femtosecond pulses at 620 nm are projected in transparent glasses.This fact was experimentally tested in Ref.[32].The parabolic nonlinearity can also be referred as cubic-quintic nonlinearity.The propagation of solitons in BF with 4WM and STD for parabolic law is described by the following v-GNLSE[32]

where ?l, σl,and νl,for l=1,2,are the coefficients of quintic nonlinearity.

Now using the wave transformation given in Eq.(3)to Eqs.(32)and(33),we get

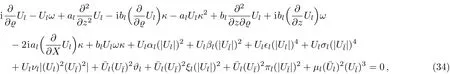
3.1 Dark-in-the-Bright Soliton

In order to extract dipole soliton solution of Eq.(34)we will again suppose the complex ansatz given in Eq.(6)and repeat the same process as in above section provides a system of algebraic equations whose solution yields subsequent parametric values for ζl=0

Under parametric conditions

Equations(35)adn(36)give the velocity and wave number of solitons respectively enforcing the following constraint conditions.

Now the exact dipole soliton solution in BF with parabolic law nonlinearity,depending upon above conditions is given as

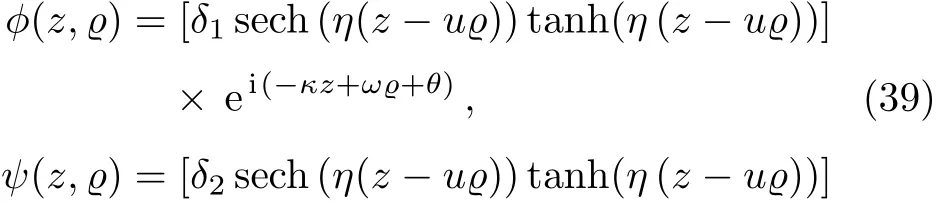
In case δl=0,we cannot reach to our desired results.

Remark 3By taking some appropriate calculations,the obtained solution in this section will meet to the solution in Ref.[38]for αl=0 and ?l=0.

3.2 Extraction of Combo Solitons

In order to get combo soliton solutions in BF with 4WM and parabolic law we will use the complex ansatz given in Eq.(21)into Eq.(34)and taking same mathematical operations as in the above section this will take us to a system of algebraic equations.Here arise again two cases,one is δl=0 and second one is ζl=0.For δl=0 solving obtained system of equations we get

In the above values u and κ give the velocity and wave frequency of solitons respectively enforcing the following constraint conditions

Now based on above parametric conditions we obtain subsequent combo soliton solution in BF with parabolic law of nonlinearity

Cinderella went immediately to gather the finest she could get, and brought it to her godmother, not being able to imagine how this pumpkin could make her go to the ball. Her godmother scooped24 out all the inside of it, having left nothing but the rind; which done, she struck it with her wand,30 and the pumpkin was instantly turned into a fine coach,31 gilded25 all over with gold.32

Now solving the system for ζl=0,we get

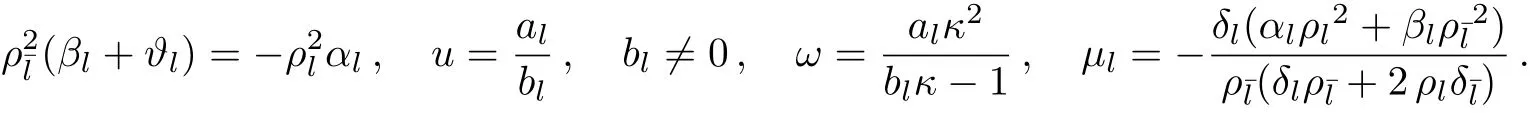
Here u and ω give the velocity and wave number of solitons respectively enforcing the following constraint conditions

Now based on above parametric conditions we obtain subsequent combo soliton solution in BF with parabolic law of nonlinearity

The intensity and the nonlinear phase shift of the above solutions are defined through Eqs.(22)and(23)respectively.It is reported that there are some difference between combo solitons and continuous waves.The first one is combo soliton have nonlinear phase shift and the second one is that obtained combo solitons should exist only in nonlinear media whereas continuous waves can exist for both linear and nonlinear media.[39]

Remark 4As far as we know that the solutions obtained in this section are all new and reported for the time.

4 Results and Discussion

This section is account for detailed discussion of the obtained results in Secs.2 and 3 along with their graphical representations.In above sections we have used two different types of complex ansatz to extract dipole,bright and combo soliton solutions of v-GNLSE with Kerr law and parabolic law nonlinearities along with STD,detuning and 4WM effects.The complex valued functions ?(z,?)and ψ(z,?)are used to represent the solitary wave profile for BF.

Equations(19)and(20)represent the dipole soliton solutions for Kerr law nonlinearity with arbitrary parameters al,bl,δl,η,κ,λl,and θ for l=1,2 respectively.Figure 1(a)demonstrates the solitary profile for the modulus of Eq.(19)(|?(z,?)|)with the choice of arbitrary parameters a1=0.8,b1=1.6,δ1=0.2,η =1,κ =1,λ1=0.6,θ=1,and Fig.1(b)depicts the 2D profile for|?(z,?)|at the instant ?=1 with the same choice of parameters as in Fig.1(a).According to the conditions given in Eq.(18)the solitary profile of Eq.(20)(|ψ(z,?)|)is like similar to Eq.(19)for the same choice of parameters.In order to avoid repetition,the graph for Eq.(20)is not presented.

Bright-dark combo soliton solutions for Kerr law is presented through Eqs.(30)and(31)with arbitrary parameters al,bl,ρl,η,ω,λl,δland θ for l=1,2 respectively.Figure 3 represents the 1-bright and 1-dark soliton solution for the modulus of Eq.(30)(|?(z,?)|)explicitly at the instant ?=1.The blue solid line is for 1-bright soliton and red dash line is for 1-dark soliton.The graph for Eq.(31)is not presented due to same physical appearance incorporating with the conditions given in Eq.(29).

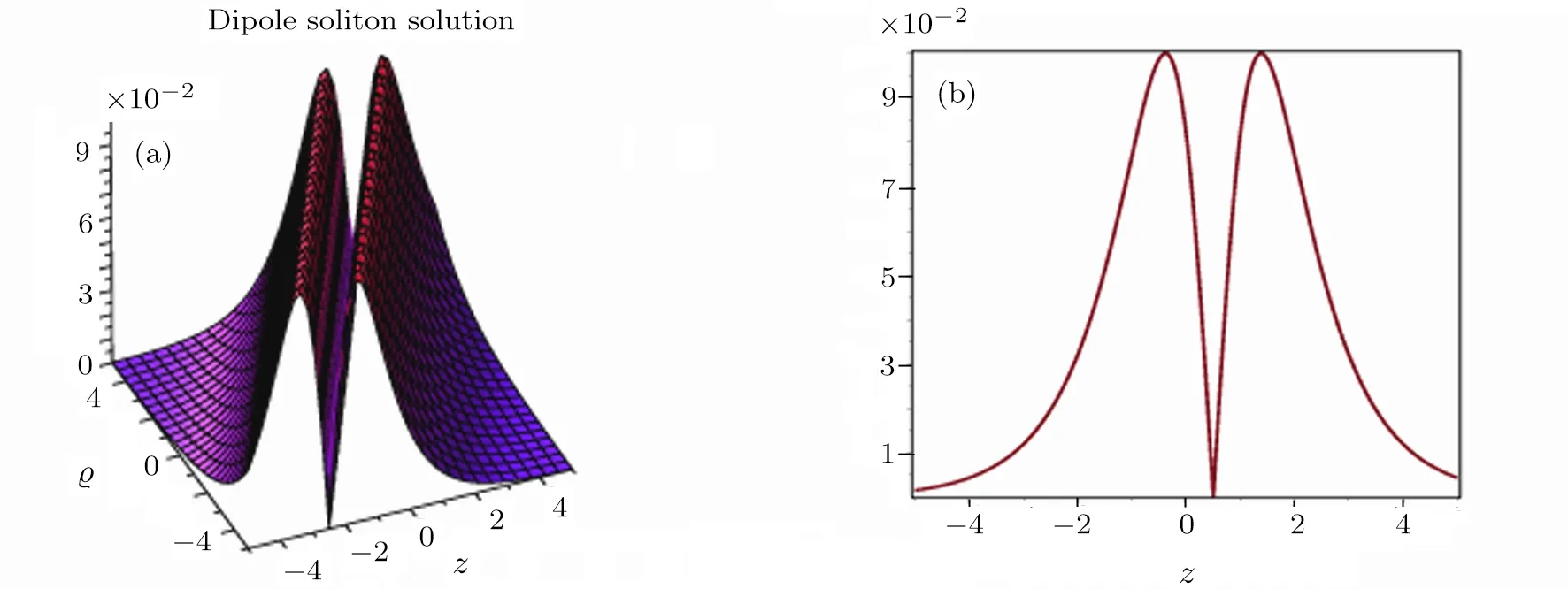
Fig.1 3D and 2D graphical representation of dipole soliton solution given in Eq.(19).(a)|?(z,?)|,a1=0.8,b1=1.6,δ1=0.2,η =1,κ =1,λ1=0.6,θ=1.(b)|?(z,1)|,a1=0.8,b1=1.6,δ1=0.2,η =1,κ =1,λ1=0.6,θ=1,?=1.

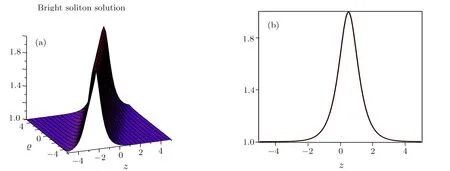
Fig.2 3D and 2D graphical depiction of bright soliton solution given in Eq.(27).(a)|?(z,?)|,a1=0.8,b1=1.6,ρ1=0.2,η =1,ω =1,λ1=0.6,θ=1,ζ1=1.(b)|?(z,1)|,a1=0.8,b1=1.6,ρ1=0.2,η =1,ω =1,λ1=0.6,θ=1,ζ1=1,? =1.

Fig.3 2D representation of bright-dark combo soliton solution given in Eq.(30).|?(z,1)|,a1=0.8,b1=1.6,ρ1=1.5,η =3,κ =1,λ1=0.6,θ=1,δ1=1.5,μ =1,?=1.

A comparative discussion can also made for parabolic law as made for Kerr law.Figures 4,5,and 6 depict the graphical representation to the intensity relations of solutions obtained for parabolic law.Equations(6)and(21)are the two complex ansatz used to obtain solitary wave solutions.The complex part in Eq.(6)provides a non-zero background for the solitary wave when the time variable tends to infinity while the real part of Eq.(6)provides the propagation of dark pulse with finite bright background width also known as dark-in-the bright soliton.[37]On the other hand imaginary part of Eq.(21)represents the bright solitary wave along with the grayness term and real part provides the dark solitary wave.[39]The amplitude and nonlinear phase shift of the solitry wave is defined through the modulus and the argument of the complex ansatz respectively.[37,39]

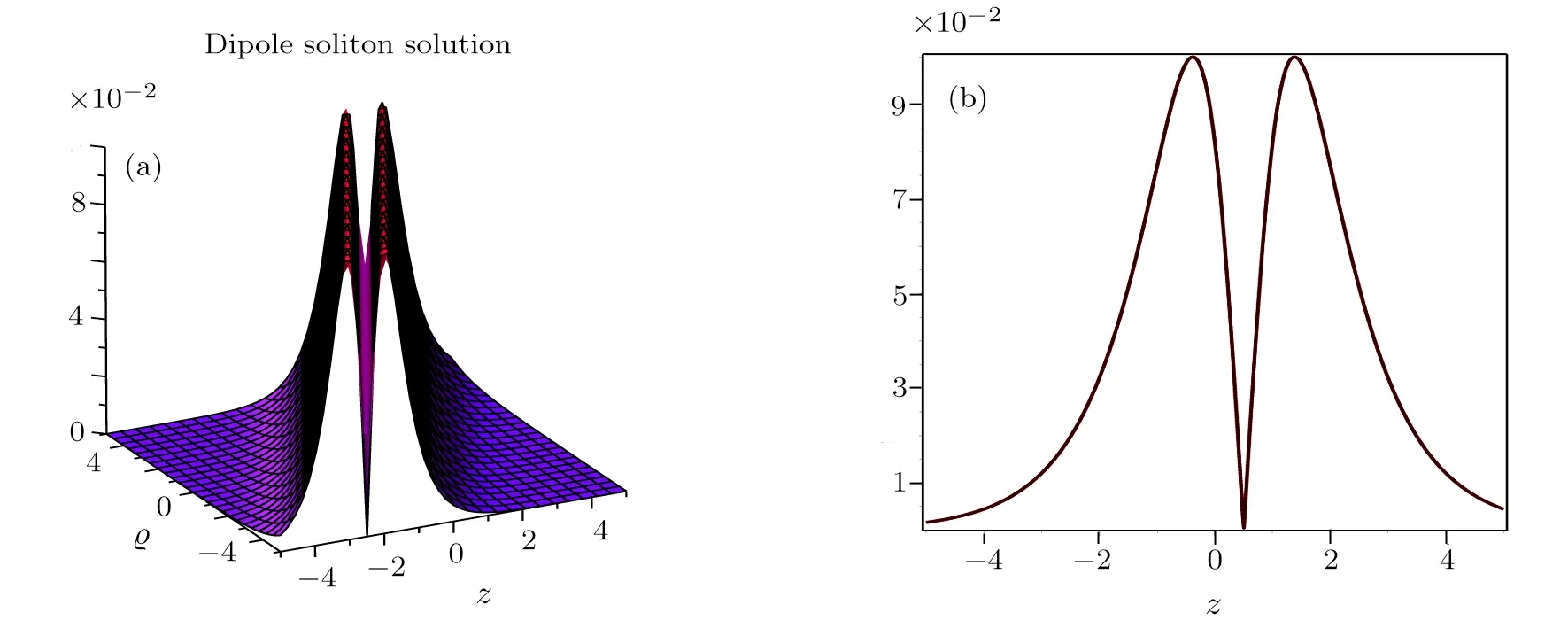
Fig.4 3D and 2D graphical representation of dipole soliton solution given in Eq.(39).(a)|?(z,?)|,a1=0.5,b1=1,δ1=0.2,η =1.7,κ =1,λ1=0.6,θ =1.(b)|?(z,1)|,a1=0.5,b1=1,δ1=0.2,η =1.7,κ =1,λ1=0.6,θ=1,?=1.

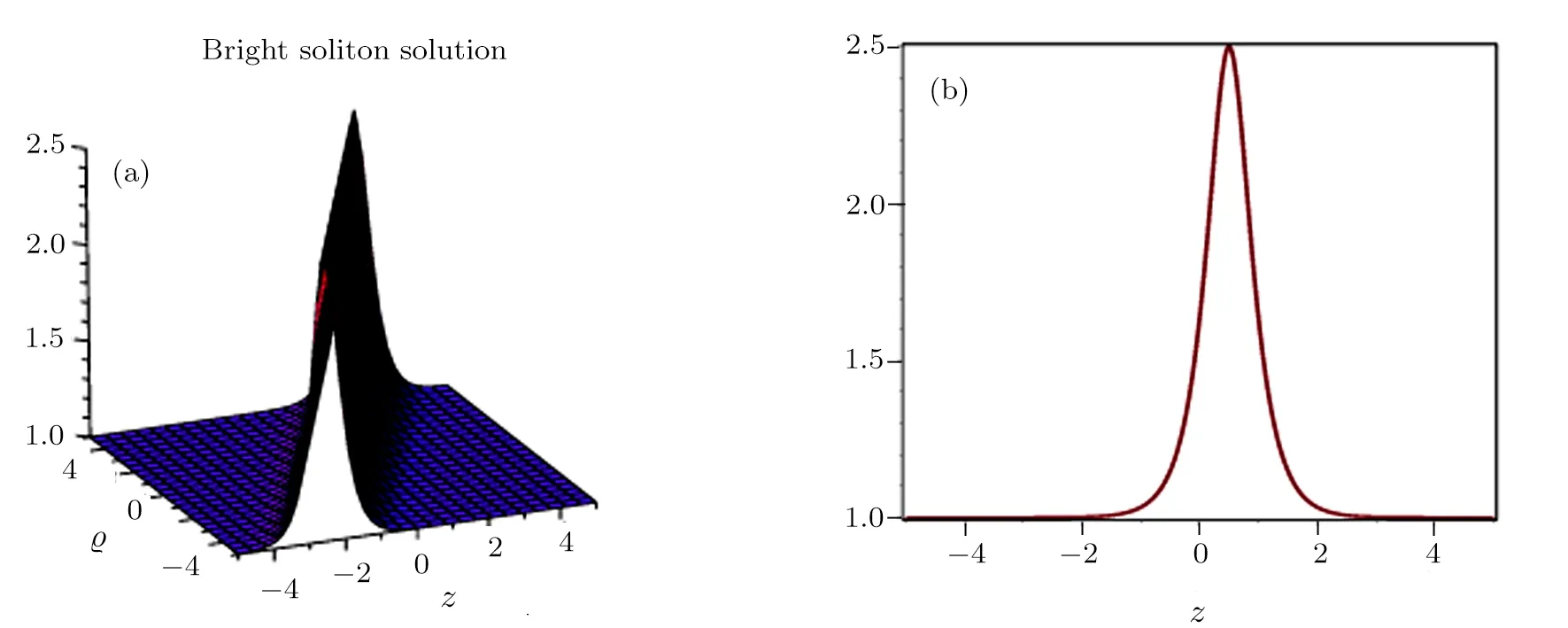
Fig.5 3D and 2D graphical representation of bright soliton solution given in Eq.(42).(a)|?(z,?)|,a1=0.8,b1=1.6,ρ1=1.2,η =3,ω =1,λ1=0.6,θ =1,ζ1=1.(b)|?(z,1)|,a1=0.8,b1=1.6,ρ1=1.2,η =3,ω =1,λ1=0.6,θ=1,ζ1=1,? =1.

Fig.6 2D representation of bright-dark combo soliton solution given in Eq.(45).|?(z,1)|,a1=1,b1=1.6,ρ1=1,η =3,κ =1,λ1=0.6,θ =1,δ1=1,μ =1,?=1.

5 Conclusion

In this article dipole and combo soliton solution in BF with the effect of 4WM have been retrieved successfully.These solutions have been extracted in the presence of Kerr and parabolic law nonlinearities. Ansztz methods of Choudhuri and Li have been implemented to extract dark-in-the-bright and bright-dark combo soliton solutions.The intensity relation and phase shift of extracted solutions have also been discussed.Further this study is useful to understand the dynamics of soliton interaction with continuous or pulsed waves occurring in highly complex and nonlinear phenomena such as rough wave formation or supercontinuum generation.