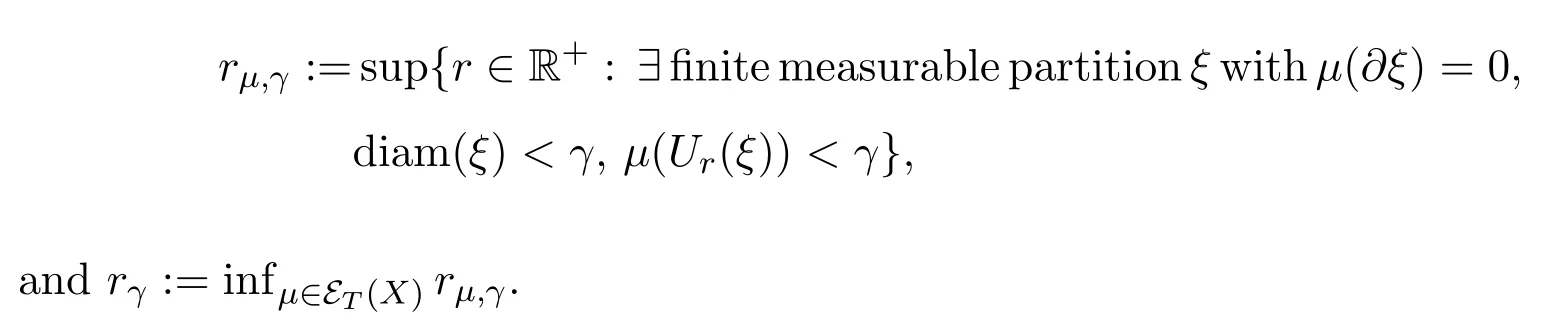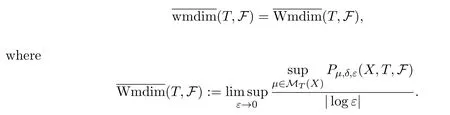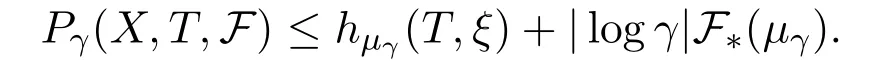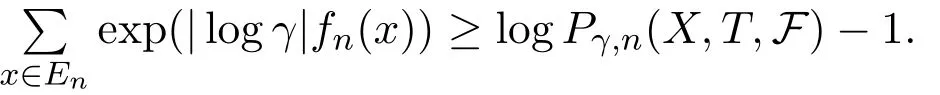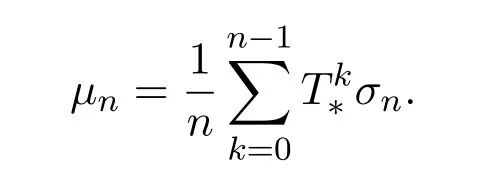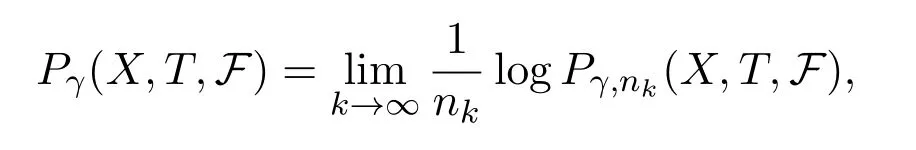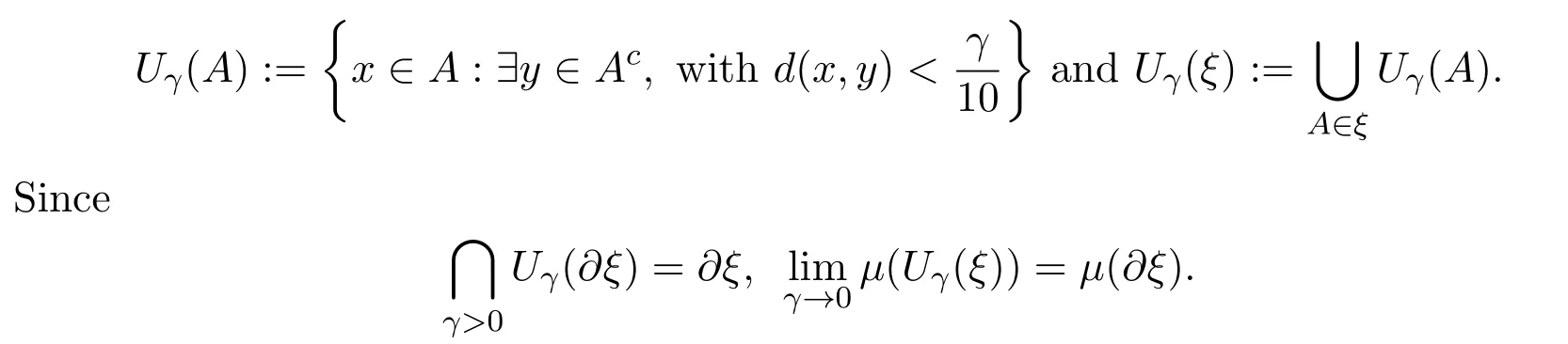Ding Zhihui,Li Zhiming

(School of Mathematics,Northwest University,Xi′an 710127,China)

Abstract：In this paper we introduce the notion of subadditive weighted upper metric mean dimension and weighted upper measure-theoretic mean dimension which are analogs of pressures.A variational principle of subadditive weighted upper mean dimensions is presented.

Keywords：subadditive potentials,weighted upper mean dimensions,variational principle

1 Introduction

Entropies and pressures are important invariants in the study of dynamical systems and ergodic theory.They are all the measurements of the complexity of the orbit structure of the system.It is then natural to consider a dynamical quantity that distinguishes systems with infinite topological entropy.The mean dimension is a meaningful quantity when the topological entropy is infinite reference[1].This invariant was introduced by Gromov in reference[2],and further studied by E.Lindenstrauss and B.Weiss in reference[3-4].This invariant has found many applications to embedding problems,in other words to the problem of when a dynamical system can be embedded into another or not,see for instance reference[1,5-6]and references therein.In this paper we introduce the notions of subadditive weighted upper metric mean dimension and subadditive weighted upper measure-theoretic mean dimension which are analogs of pressures.Weighted upper metric mean dimensionof a sequence of functionsF={fn}n≥1are extensions of the weighted upper metric mean dimension wmdimZ(f)of a single functionf.A variational principle of subadditive weighted upper mean dimensions is presented.

More precisely,suppose thatT:X→Xis a continuous map on a compact metric space(X,d)andF={fn}n≥1is a subadditive sequence of continuous functions,whereFsatisfies the subadditive condition:fn+m(x)≤fn(x)+fm(Tnx),?m,n∈N.We denote the cardinal number of a setSby card(S).For eachn∈N,set

Let B be theσ-algebra of Borel subsets ofXandMT(X)the set ofT-invariant Borel probability measures.LetET(X)?MT(X)be the set of ergodic measures.

Definition 1.1For anym,n∈N andε>0,letE,F,K?X,if for anyx∈Kthere existsy∈Fsuch thatdn(x,y)≤ε,then we callFan(n,ε)spanning set ofK.LetE?K,if for anyx,y∈Ewe havedn(x,y)>ε,then we callEan(n,ε)separated set ofK.

Ifsε,n(X,T)is the maximal cardinality of an(n,ε)separated subset ofXandrε,n(X,T)is the smallest cardinality of an(n,ε)spanning subset ofX,

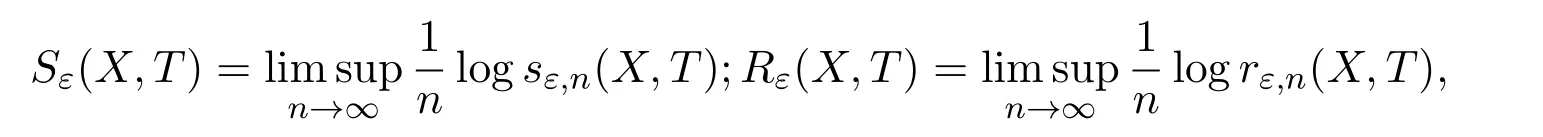
then topological entropy is defined as

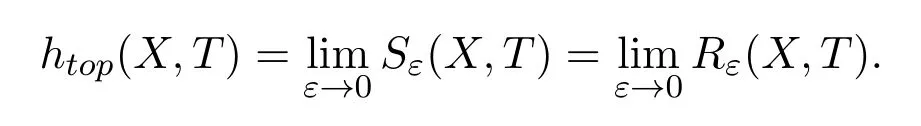
The topological entropy is known to be independent of the compatible metricdsinceXis compact.The upper metric mean dimension is defined as

Recently Reference[5]established a variational principle for upper metric mean dimension under some conditions on the space.

Condition IA compact metric space(X,d)is said to have tame growth of covering numbers if for everyδ>0,we havelogcard(X,d,ε)=0,where card(X,d,ε)is the minimum cardinality of an open cover with diameter smaller thanε.

Variational principle I[5]LetT:X→Xbe a continuous map on a compact metric space(X,d).Supposedsatisfies Condition I.Then

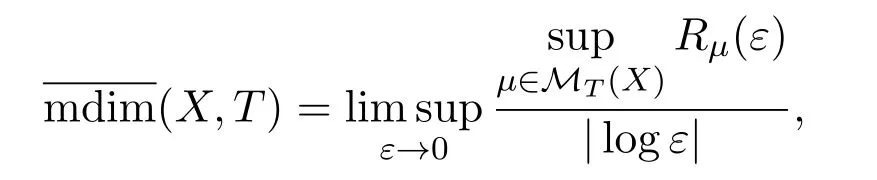
whereRμ(ε)is rate distortion function,we refer reference[5]for the precise definitions.

Forμ∈MT(X)defineNμ,δ,ε,n(X,T)as the minimum number of(n,ε)-dynamical balls needed to cover a set of measure strictly bigger than 1?δ.Then define

It was proven in reference[2]thatfor everyμ∈ET(X)and anyδ∈(0,1),wherehμ(T)is the measure theoretic entropy ofμ(For precise definition see Definition in reference[7]).They proved the following result.

Variational principle II[4]Let(X,d)be a compact metric space andT:X→Xcontinuous.Then

2 Subadditive weighted upper mean dimension

Next we introduce the notion of subadditive weighted upper metric mean dimension and subadditive weighted upper measure-theoretic mean dimension which are analogs of pressures.For anyε>0,letF={fn}n≥1be a subadditive sequence of continuous functions.

Remark 2.1(1)0≤Qε,n(X,T,F)≤‖exp(|logε|fn)‖rε,n(X,T),

0≤Pε,n(X,T,F)≤‖exp(|logε|fn)‖sε,n(X,T).

(2)Ifε1≤ε2thenPε2,n(X,T,F)≤Pε1,n(X,T,F),Qε2,n(X,T,F)≤Qε1,n(X,T,F).

(3)Pε,n(X,T,0)=sε,n(X,T),Qε,n(X,T,0)=rε,n(X,T).

(4)Qε,n(X,T,F)≤Pε,n(X,T,F).

For subadditive sequence of continuous functionsF,ε>0,put

Then we let

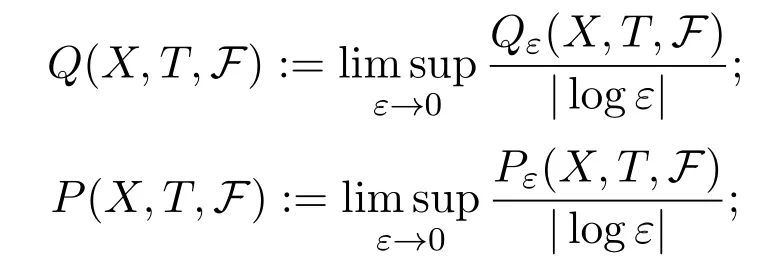
Definition 2.1For subadditive potentialF,is called weighted upper metric mean dimension ofTwith respect toF.

In this paper,we assume that the familyFsatisfies the following bounded distortion assumption:

andBn(x,ε)={y∈X:dn(x,y)<ε}.

Lemma 2.1LetFis a subadditive potential,if Standing hypothesis is satisfied,thenP(X,T,F)≤Q(X,T,F).

ProofLetEbe an(n,ε)separated set andFanspanning set.Define?:E→Fby choosing for eachx∈E,some point?(x)∈Fwith.Then?is injective and

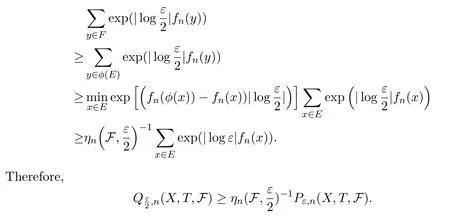
Together with the Standing hypothesis,impliesP(X,T,F)≤Q(X,T,F).This,we complete the proof.

Proposition 2.1For subadditive sequence of continuous functionsFwhich satisfies the standing hypthesis,Q(X,T,F)=P(X,T,F).

ProofBy Remark 2.1(4),Q(X,T,F)≤P(X,T,F).One the other hand,by Lemma 2.1,P(X,T,F)≤Q(X,T,F).This,we finish the proof.

For any invariant measureμ∈MT(X),ε>0,0<δ<1,we put

For subadditive potentialF,ε>0 and 0<δ<1,put

For any finite measurable partitionξof(X,B)and anyμ∈MT(X),write

Definition 2.2AssumeT:X→Xis a measure preserving transformation,μ∈MT(X),we call

the measure-theoretic entropy ofTwith respect toμ.

Proposition 2.2For subadditive potentialFsatisfies Standing hypothesis,

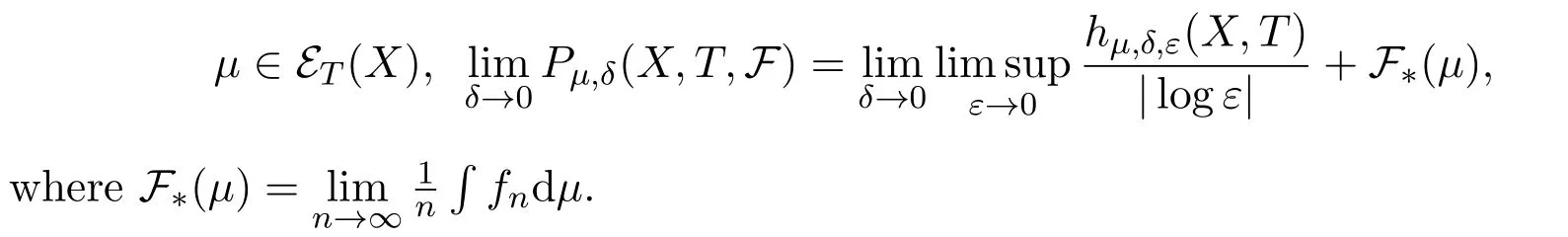
ProofThe proof is further divided into two steps.

Step 1:First,we show

Sinceμis ergodic,by subadditive ergodic theorem and Egorov theorem,there is a measurable setB∈B withsatisfies the following:For everyi∈N there existsNi∈N such that for anyn≥Ni,x∈B,.

We choose a sequence of positive integer{ni}i∈Nsatisfies:

(I)ni≥Ni,for anyi∈N;

(III)LetCnibe a set withandDnian(ni,ε)spanning set ofCniwith.

PutEni=B∩Cni,thenμ(Eni)>1?δ.LetFni?Dnibe an(ni,ε)spanning set ofEniwith smallest cardinality.Thus for anyx∈Fni,there is Φ(x)∈Enisuch thatdni(x,Φ(x))<ε.Therefore,

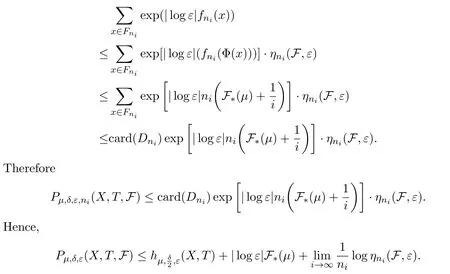
Dividing by|logε|and letε→0,by Standing hypothesis,we have(1).

Step 2:Next,we show

Again by subadditive ergodic theorem and Egorov theorem,similar to Step 1 we can find a measurable setB∈B withμ(B)>1?δand a sequence of positive integer{ni}i∈Nsatisfies the following:For everyi∈N there existsNi∈N such that for anyi∈N,x∈B,

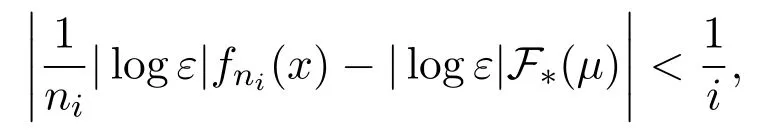
and

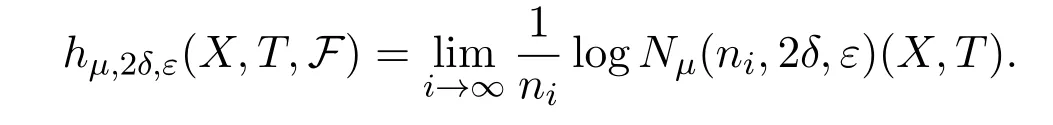
LetCnibe a set withμ(Cni)>1?δandDnian(ni,ε)spanning set ofCni.PutEni=B∩Cni,thenμ(Eni)>1?2δ.LetFni?Dnibe an(ni,ε)spanning set ofEniwith smallest cardinality.Thus for anyx∈Fni,there is Φ(x)∈Enisuch thatdni(x,Φ(x))<ε.Therefore,

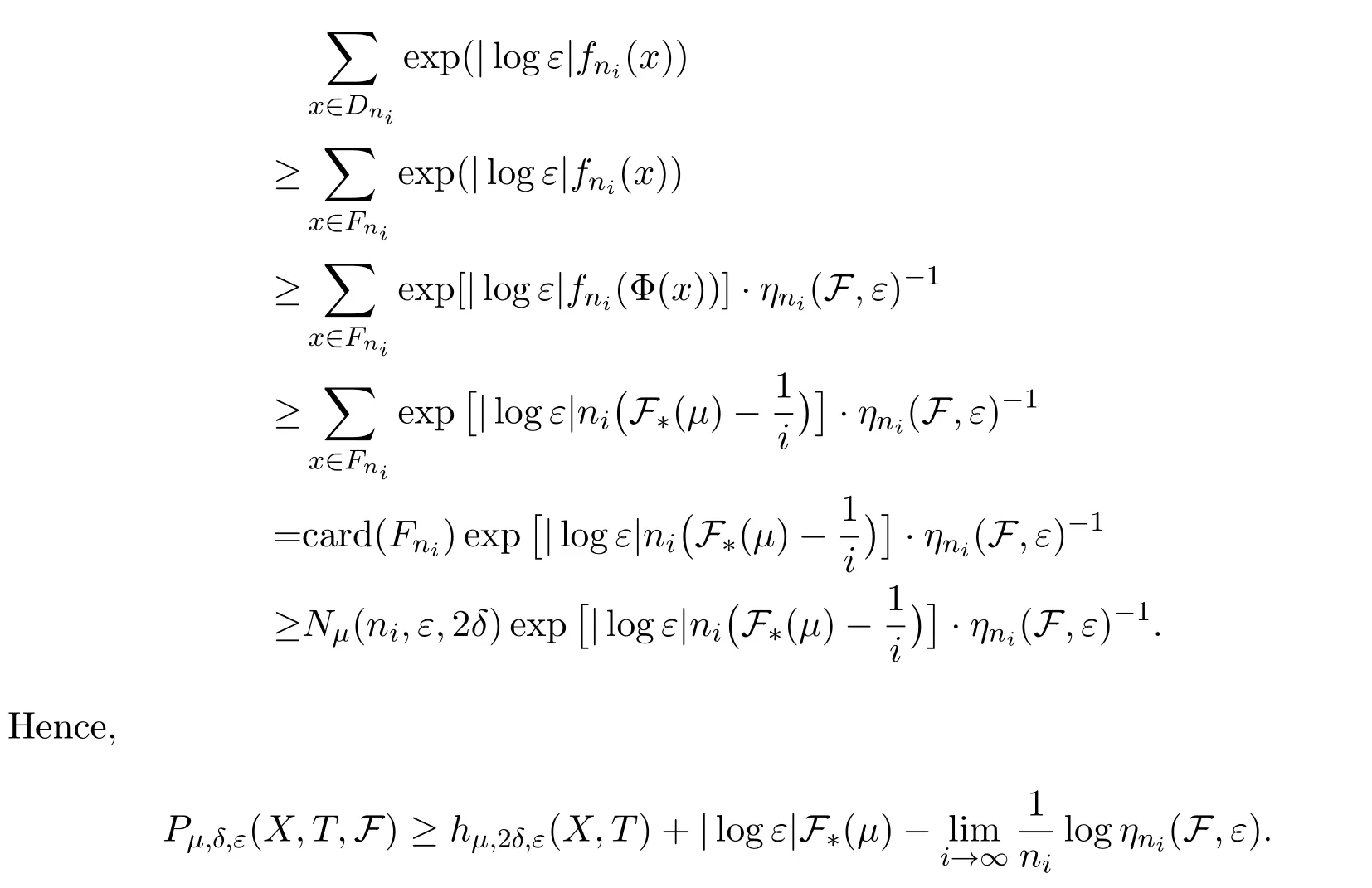
Dividing by|logε|and lettingε→0,and by Standing hypothesis,we have(2).Thus we finish the proof.

3 Variational principle

For any finite measurable partitionξandr>0,let

If a finite measurable partitionξsatisfiesμ(?ξ)=0 for someμ∈ET(X),then for anyγ>0,we can find 0

Condition IIFor anyγ>0,rγ>0 and

Theorem 3.1Let(X,d)be a compact metric space,T:X→Xcontinuous.For subadditive potentialFand 0<δ<1,if(X,T)satisfies Condition II,then

Before prove the theorem 3.1,we need the following lemma.

Lemma 3.1For anyγ>0,there existsμγ∈ET(X)such that for all finite measurable partitionξwith diam(ξ)<γandμγ(?ξ)=0,we have

whereδxis the probability measure supported atx.Then define

Consider a subsequence{nk}k∈Nsuch that

and{μnk}k∈Nconverges to someμ∈MT(X).Letξbe a finite measurable partition with diam(ξ)<γandμ(?ξ)=0.Since each element ofξncontains at most one element ofEn,by the definition ofσnand Lemma 9.9 in reference[8],we have

The rest of the lemma follows by ergodic decomposition theorem in reference[8],we can chooseμγ∈ET(X)satisfies the desired properties.

Proof of Theorem 3.1The inequalityfollows directly from definitions.

Letξbe a finite measurable partition and?A,where?Ais the boundary ofA.Forγ>0,let

We choose a finite measurable partitionξwithμ(?ξ)=0.We can assume,and find 0<γ<εsuch that.By the proof of Theorem 1.1 in reference[7],there isN1∈N such that for anyn>N1,

Again by subadditive ergodic theorem and Egorov theorem,similarly we can find a measurable setB∈B withand a sequence of positive integer{ni}i∈Nsatisfies the following:

For everyi∈N there existsNi∈N such that for anyi∈N,x∈B,

LetCnibe a set withandDnian(ni,γ)spanning set ofCni.PutEni=B∩Cni,thenμ(Eni)>1?δ.LetFni?Dnibe an(ni,γ)spanning set ofEniwith smallest cardinality.Thus for anyx∈Fni,there is?(x)∈Enisuch thatdni(x,?(x))<γ.Therefore,

By Lemma 3.1,we have

Divided by|logγ|and letε→0.Sinceε>γ>0 and by Condition II and Standing hypothesis,we have