Zi-Yang Qiu(邱子陽),Zhi-Yu Liao(廖知裕),and Xiang-Gang Qiu(邱祥岡),3,?

1Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

3Collaborative Innovation Center of Quantum Matter,Beijing 100084,China

1.Introduction

In the past few years,a great deal of interest has been aroused in topological materials with magnetic systems that can break their time-reversal symmetry,resulting in the realization of type-II Weyl fermions.[1,2]Even though many materials are theoretically predicted as type-II Weyl semimetals,only a few have been experimentally confirmed.[3,4]Recently,AMnBi2and AMnSb2(A=Ca,Sr,Ba,Eu,and Yb)compounds have attracted much attention due to the antiferromagnetic order on Mn atoms.[5–18]Among these materials,SrMnBi2,CaMnSb2,and SrMnSb2share the same crystal symmetry and stacking type.Additionally,the band structures of these three materials have been calculated in detail,[8,17,19]and their electronic bands near the Fermi level are roughly identical. However,unlike the two-Drude model,which well describes the real part of optical conductivity σ1(ω)of CaMnSb2and SrMnBi2at low frequency,[17,20]a single-band Drude model introduced in Ref.[21]lacks detailed fitting σ1(ω)of SrMnSb2.Therefore,more optical studies in the low frequency range are required for SrMnSb2.

We successfully synthesize the single crystal of SrMnSb2and investigate its topological properties through infrared spectroscopy.Because of the unusual linearly dispersed band structures in topological materials,the optical conductivity of the interband transitions near the Fermi level are supposed to follow a characteristic power-law frequency dependence,

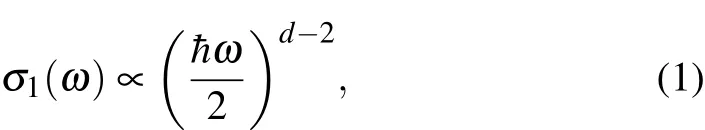
where d is the dimension of the system.[1,22–24]Thus,when d=2,σ1(ω)is particularly frequency-independent,while for d=3,σ1(ω)should have a linearly increased range and extrapolates through the origin.In this paper,we observed a shift of the plasma minimum with varying temperature.A linearly increased component in σ1(ω)has been identified with extrapolating to zero conductivity at finite frequency,which agrees well with theoretical calculations.In the low frequency range,we introduce a two-Drude model to describe σ1(ω)excellently.Therefore,the shift of the plasma minimum can be the result of a narrow Drude term which varies with temperature.The contributions of two Drude in dc conductivity have been separated,and the transport properties of SrMnSb2are mainly affected by the narrow-Drude quasiparticles.Since the two-Drude model can reasonably explain the optical and transport properties,we can infer that the two-Drude model is an appropriate approach to investigate the multiband materials in AMnSb2and AMnBi2families.

2.Experiment

The self- flux method was used to synthesize high-quality single crystals of SrMnSb2.[25]The ab-plane reflectivity[R(ω)]has been measured at a near-normal angle of incidence on a Bruker IFS80v spectrometer using an in situ gold over filling technique.[26]Data from 50 cm?1to 15000 cm?1were collected at 14 different temperatures from 7 K to 295 K.R(ω)up to 30000 cm?1was measured at room temperature with an Avaspec 2048×14 optical fiber spectrometer.Optical conductivity was calculated through Kramers–Kronig transformation of R(ω).For the low-frequency extrapolation,we used a set of Lorentz oscillators instead of the Hagen–Rubens form because of the very narrow scattering rate of the Drude component.[16,27]Above 30000 cm?1,R(ω)is assumed to be constant up to 12.4 eV,above which a free-electron response(ω?4)is used.

3.Results

3.1.Reflectivity

Figure 1 shows R(ω)of SrMnSb2up to 4000 cm?1at all measured temperatures.The obvious peakat around 200 cm?1is a response of infrared active phonon.The typical metal behavior is detected when R(ω)rapidly approaches unity,and a low-frequency sharp plasma edge shifts to higher frequency upon cooling.In addition,the minimum measured reflectance,defined as the plasma minimum,exhibits a strong temperature dependence in R(ω):as temperature is increased,the plasma minimum initially keeps constant and then red shifts,as denoted in the upper inset of Fig.1.This change of the plasma minimum is usually associated with the temperature evolution of the carrier density.

Fig.1.Reflectivity of SrMnSb2below 4000 cm?1at all measured temperatures.The upper inset denotes the evolution of plasma minima.The bottom inset shows the reflectivity up to 30000 cm?1at 295 K.The red-dashed curve is the low frequency extrapolation.

3.2.Optical conductivity

Figure 2 displays σ1(ω)of SrMnSb2at four represented temperatures.In the low-frequency range,σ1(ω)shows obvious Drude-like response,which becomes broad when the temperature is increased.σ1(ω)up to 30000 cm?1is shown in the inset of bottom panel.We can infer the low carrier density from the small Drude weight compared with conventional metals.[28]Additionally,an important clue of Dirac dispersed electronic bands is that one linearly-increased optical conductivity(3000 cm?1–4500 cm?1)can be clearly recognized in the spectrum,alongside a sharp absorption edge from 2500 cm?1to 3000 cm?1.The linearly increased optical conductivity is denoted by a black dashed line in the upper inset of Fig.2(a).The extrapolation to zero conductivity at finite frequency indicates the gapped Dirac band structure,which is consistent with the theoretical calculation in Ref.[21].

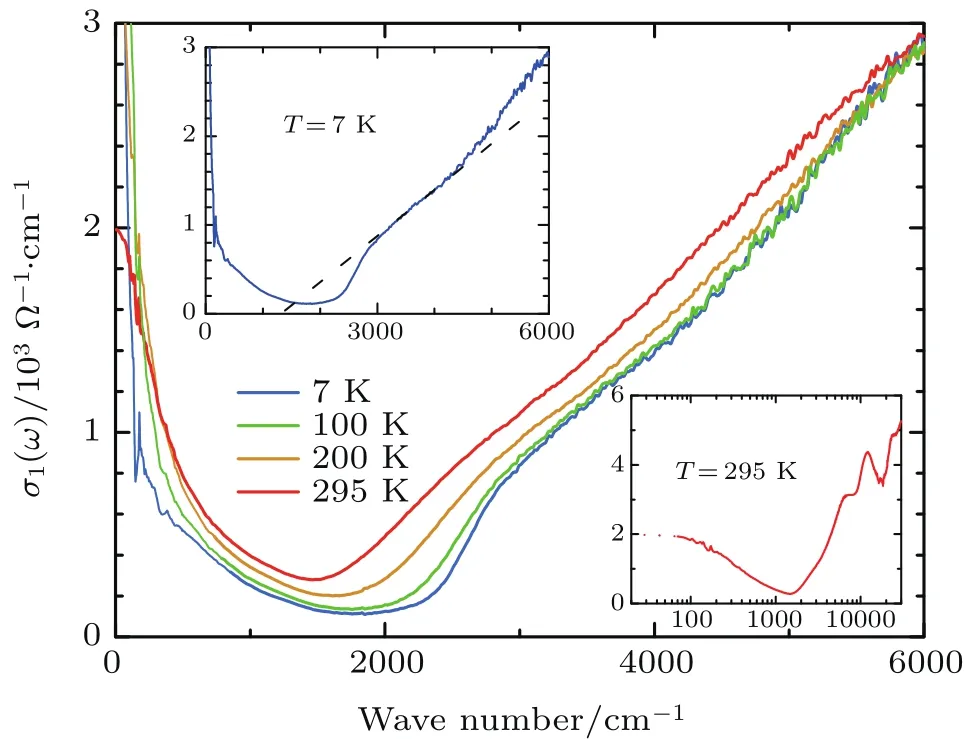
Fig.2.The real part of optical conductivity σ1(ω)of SrMnSb2at four represented temperatures.The upper inset of the panel displays the linear σ1(ω)denoted with the black-dashed line.The bottom inset shows σ1(ω)up to 30000 cm?1at 295 K.

3.3.Low frequency fit

To quantitatively analyze the electrodynamic response,the typical Drude–Lorentz model[29]is employed to fit the low-frequency σ1(ω):

where Z=377 ? is the vacuum impedance. The first term is a sum of free-carrier Drude responses,whereis the plasma frequency(n is a carrier density and m?is an effective mass),and 1/τ is the scattering rate of carriers.The second term describes a sum of Lorentz oscillators,with ωj,γj,and ?jbeing the resonance frequency,line width and oscillator strength.

In Ref.[21],Park et al.suggests a single-band Drude model at low frequency.Once we have attempted to fit the measured σ1(ω)with one Drude model at various temperatures,the Drude-like response narrows upon cooling,which results in the fitting at the tail of Drude response being far from satisfactory.We should know that more parameters can produce different fitting results,which would make our analysis unreliable.So in our fitting,the number of parameters is used as little as possible to fit σ1(ω)at low frequency.Therefore,a two-Drude-component model with four parameters is introduced to describe σ1(ω)well at all measured temperatures,as displayed in Fig.3(a).This two-Drude-component model coincides with the multiple Fermi surface near EFin SrMnSb2,which has been theoretically demonstrated in Ref.[19].The interpret conductivity of the model extrapolated to zero-frequency is plotted in the inset of Fig.3(a).The good agreement when compared to the measured dc resistivity(black solid curve)implies the fitting is reliable.

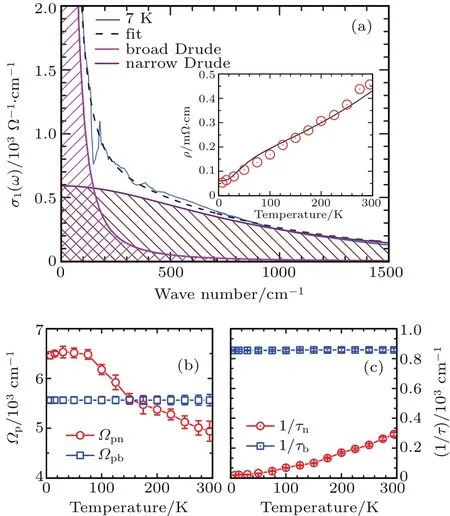
Fig.3.(a)The blue-solid curve is the optical conductivity of SrMnSb2 at7K in the 0cm?1–1500cm?1range.The black-dashed curve through the data is the fit which is decomposed into a narrow(magenta)and a broad(purple)Drude terms.The inset is the comparison of the measured dc resistivity(solid curve)with the inverse of the zero-frequency conductivity by fittingσ1(ω)(redcircles).Panels(b)and(c)portray the plasma frequency ?pand scattering rate 1/τ for the two Drude components as a function of temperature.

The plasma frequency ?pand the scattering rate 1/τ as a function of temperature for the two Drude components can be extracted by modeling the optical data.The temperature evolution of ?p,which is related to the carrier density,is traced out in Fig.3(b).Within error bars,?p’s of broad Drude component(?pb)is roughly constant,suggesting that the carrier density does not change at various temperatures,while the?p’s of narrow Drude component(?pn)initially keeps constant and then increases slowly with the increasing temperature.Since ?pnchanges with temperature,the spectral weight of Drude response is not constant but rather transfers to higher frequency as T is raised.Moreover,for the resembling temperature dependence of ?pn,we can infer that the T-dependent shifts in plasma minimum is solely triggered by the narrow Drude component.Figure 3(c)portrays 1/τ as a function of the temperature.For narrow Drudecomponent,1/τndecreases from 300 cm?1to 20 cm?1upon cooling,but for broad Drude,1/τbstill exhibits no temperature dependence.The different temperature evolution of ?pand 1/τ for the two Drude components evinces the two types of carriers in this material,which have different contributions to the transport properties of SrMnSb2.

To obtain further confirmation,we extract σ1(ω)at zero frequency to separate the two Drude terms’contributions to the dc conductivity in Fig.4(a).We observed σ1n(0)decreases with increased temperature,while σ1b(0)remains constant.Since the two Drude terms affect dc conductivity through σtotal(T)= σn(T)+ σb(T),the fact that σ1n(0)> σ1b(0)across all the measured temperature range indicates the quasiparticles of narrow Drude has more effect on the transport properties.Figure 4(b)portrays the two Drude corresponding resistivity yielded from the inverse of σ1(0).Even though ρb(T)exhibits no temperature dependence,ρn(T)shows a roughly identical temperature evolution to the dc resistivity in the inset of Fig.3(a).These results demonstrate that the quasiparticles of the narrow Drude plays a major role in the transport properties.

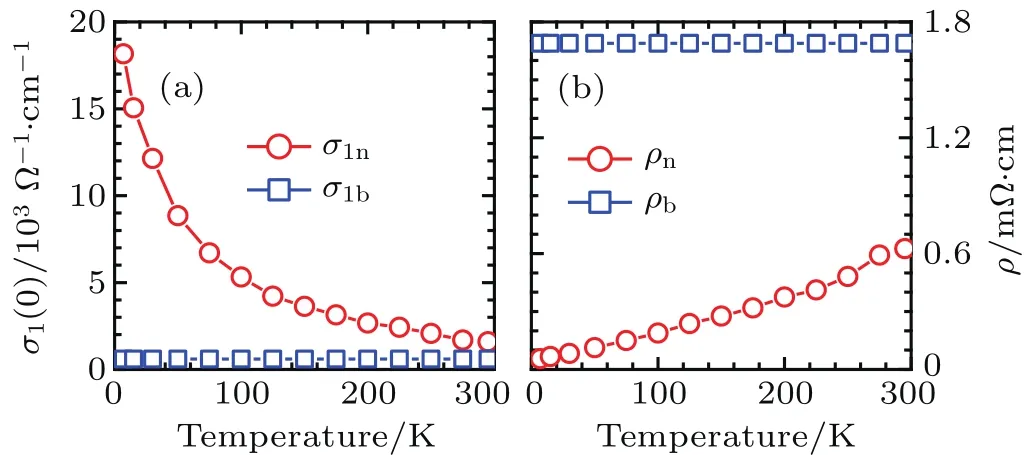
Fig.4.(a)The contribution to dc conductivity σ1(ω → 0)at varied temperatures.(b)The corresponding resistivity through ρ =1/σ1(ω → 0)for the narrow and broad Drude components.

Since in Ref.[30]Ling et al.points out that the carrier types of SrMnSb2is sensitive to the composition and growth details,it is reasonable for us to only consider the carriers’different contributions to the conductivity,and separate them into two Drude quasi-particles with different temperature dependence instead of hole or electron carriers. The carriers of broad Drude with constant scattering rate and plasma frequency at all measured temperature can produces an incoherent contribution to the conductivity,while the carriers of narrow Drude component plays a major role in dc conductivity and can explain the optical data well in our measurement.Therefore,the two different types of carriers belong to the different contributions to the conductivity.

4.Conclusion

To summarize,the detailed optical properties of SrMnSb2have been measured from 7 K to 295 K.We observe the plasma minimum initially keeps constant and then red shifts with the increasing temperature in reflectivity,which infers that the carrier density varies with temperature.One linearly-increased component in optical spectrum has been recognized as the characteristic hallmark of a three-dimensional Dirac dispersed band structure.The finite intercept obtained through extrapolating the linear component to zero frequency indicates the gapped nature in Dirac bands,which coincides with theoretical calculations.The low-frequency optical conductivity is well-described by the superposition of two Drude components,suggesting the multiple Fermi surfaces in this material.We extract the plasma frequency and scattering rate for the two Drude terms as a function of temperature by fitting the optical data.Since the similar temperature evolution of plasma frequency observed for narrow Drude term,the T-dependent shifts of plasma minimum can be explained-well by the narrow Drude component.In addition,the contribution of the two group carriers to the dc conductivity has been traced out,and the narrow Drude subsystem plays a major role in the transport properties.Compared with the similar response detected in CaMnSb2and SrMnBi2,all of these reasonable conclusions and results indicate that the two-Drude model is an appropriate approach to investigate the multiband material in AMnSb2and AMnBi2families.

Acknowledgments

We thank Wei Zhang for our useful discussions.

[1]Armitage N P,Mele E J and Vishwanath A 2018 Rev.Mod.Phys.90 015001

[2]Bansil A,Lin H and Das T 2016 Rev.Mod.Phys.88 021004

[3]Coulter J,Sundararaman R and Narang P 2018 Phys.Rev.B 98 115130

[4]Xu N,Wang ZW,Magrez A,Bugnon P,Berger H,Matt C E,Strocov V N,Plumb N C,Radovic M and Pomjakushina E 2018 Phys.Rev.Lett.121 136401

[5]Guo Y F,Princep A J,Zhang X,Manuel P,Khalyavin D,Mazin I I,Shi Y G,Boothroyd and A T 2014 Phys.Rev.B 90 075120

[6]Wan X,Turner A M,Vishwanath A and Savrasov S Y 2011 Phys.Rev.B 83 205101

[7]LeeG,FarhanMA,KimJSandShimJH2013Phys.Rev.B87245104

[8]Park J,Lee G,Wolff-Fabris F,Koh Y Y,Eom M J,Kim Y K,Farhan M A,Jo Y J,Kim C and Shim J H 2011 Phys.Rev.Lett.107 126402

[9]Wang K,Graf D,Wang L,Lei H,Tozer S W and Petrovic C 2012 Phys.Rev.B 85 041101

[10]Li L,Wang K,Graf D,Wang L,Wang A and Petrovic C 2016 Phys.Rev.B 93 115141

[11]Wang A,Zaliznyak I,Ren W,Wu L,Graf D,Garlea V O,Warren J B,Bozin E,Zhu Y and Petrovic C 2016 Phys.Rev.B 94 165161

[12]Wang K,Graf D,Lei H,Tozer S W and Petrovic C 2011 Phys.Rev.B 84 220401

[13]May A F,McGuire M A,Sales and B C 2014 Phys.Rev.B 90 075109

[14]Chinotti M,Pal A,Ren W J,Petrovic C and Degiorgi L 2016 Phys.Rev.B 94 245101

[15]Liu J,Hu J,Cao H,et al.2016 Sci.Rep.6 30525

[16]Chaudhuri D,Cheng B,Yaresko A,Gibson Q D,Cava R J and Armitage N P 2017 Phys.Rev.B 96 075151

[17]Qiu Z Y,Le C C,Dai Y M,Xu B,He J B,Yang R,Chen G F,Hu J P and Qiu X G 2018 Phys.Rev.B 98 115151

[18]Wang Y Y,Xu S,Sun L L and Xia T L 2018 Phys.Rev.Materials 2 021201

[19]Farhan M A,Lee G and Shim J H 2014 J.Phys.:Condens.Matter 26 042201

[20]Park H J,Park B C,Lee M C,Jeong D W,Park J,Kim J S,Ji H S,Shim J H,Kim K W,Moon S J 2017 Phys.Rev.B 96 155139

[21]Park H J,Sandilands L J,You J S,Ji H S,Sohn C H,Han J W,Moon S J,Kim K W,Shim J H and Kim J S 2016 Phys.Rev.B 93 205122

[22]Carbotte J P 2017 J.Phys.:Condens.Matter 29 045301

[23]Hosur P,Parameswaran S A and Vishwanath A 2012 Phys.Rev.Lett.108 046602

[24]Ashby P E C and Carbotte J P 2014 Phys.Rev.B 89 245121

[25]He J B,Fu Y,Zhao L X,Liang H,Chen D,Leng Y M,Wang X M,Li J,Zhang S and Xue M Q 2017 Phys.Rev.B 95 045128

[26]Homes C C,Reedyk M,Cradles D A and Timusk T 1993 Appl.Opt.32 2976

[27]Schilling M B,L?hle A,Neubauer D,Shekhar C,Felser C,Dressel M and Pronin A V 2017 Phys.Rev.B 95 155201

[28]Beach R T and Christy R W 1997 Phys.Rev.B 16 5277

[29]Dai Y M,Akrap A,Schneeloch J,Zhong R D,Liu T S,Gu G D,Li Q and Homes C C 2014 Phys.Rev.B 90 121114

[30]Ling J W,Liu Y W,Jin Z,Huang S,Wang W Y,Zhang C,Yuan X,Liu S S,Zhang E Z,Huang C,Sankar R,Chou F C,Xia Z C and Xiu F X 2018 Chin.Phys.B 27 017504