GENG Tianzhen(耿天真),MA Xiaobin(馬曉玢)

(School of Mathematics and Big Data,Anhui University of Science and Technology,Huainan 232000,China)

Abstract: Let Fnq be the n-dimensional row vector space over a finite field Fq of odd characteristic,and let Sn be a non-singular n×n symmetric matrix over Fq.The total orthogonal graph O(Sn,q) with respect to Sn is defined to be the graph with vertices of all 1-dimensional subspace of Fnq ,two vertices [α] and [β] are adjacent if and only if αSnβT≠ 0.The three types of isotropic orthogonal graphs studied in [3] are induced subgraphs of O(Sn;q) with vertices of all isotropic lines.In this paper,the automorphism group of O(Sn,q) is determined.Not like the case of isotopic orthogonal graph studied in[3] (where the graph is vertex transitive),it turns out that the vertex set of O(Sn,q) has three orbits if n is odd,and it has only two orbits if n is even.

Key words: Orthogonal graph;Graph automorphism;Transitivity

1.Introduction

Recently,some graphs based on geometry of classical groups have attracted more attention.We now list some papers concerning with such graphs.TANG and WAN[9]studied the symplectic graph over an arbitrary finite field and determined the full automorphism group.LI and WANG[6]further showed that the subconstituents of the symplectic graph are strictly Deza graphs except the trivial case whenυ= 2.Meemark and Prinyasart[8]introduced the symplectic graphSp(2υ,Zpn) and showed that it is strongly regular whenυ= 1 and it is arc transitive whenpis an odd prime.LI et al.[5]continued the research onSp(2υ,Zpn),showing thatSp(2υ,Zpn) is arc transitive for any primep,and it is a strictly Deza graph ifυ ≥2 andn ≥2.GU and WAN[2]studied the subconstituents of the symplectic graphs modulopn.WAN and ZHOU[11?12]studied the(isotropic)unitary graphs and the(isotropic)orthogonal graphs of Characteristic 2.We here particularly mention [3] due to GU,which seems much related to our topic.Forn=2υor 2υ+1 or 2υ+2,GU[3]defined the(isotropic)orthogonal graphO(n,q) with respect to a symmetric matrixoverFq,where ?=?or ?=1 or ?=diag{1,?z},in such a way: the vertex set of the graph is all isotropic lines ofFnq,two isotropic lines[α]and[β]are adjacent if and only ifαHβT≠0.GU[3]showed thatO(n,q) is strongly regular forυ ≥2,and determined the group of automorphisms ofO(n,q).By the automorphism group of the graph it is easy to see thatO(n,q) is vertex transitive and edge transitive.For more results about the graphs based on geometry of classical groups the reader may refer to [4,7,13].

One might find that the vertex set of the graphs introduced in [2-9,11-13] are taken to be isotropic lines,or sometimes totally isotropic subspaces of the space in question.In this paper,we shall use all 1-dimensional subspace (isotropic or not) of a orthogonal space to define a new graph,which includes the isotropic orthogonal graph as an induced subgraph.The vertex set of the graph chosen in such a way seems much natural.Indeed,the vertex set of the earliest graph studied by TANG and WAN,i.e.,the symplectic graph,is taken to be all 1-dimensional subspace (although,it can be also viewed consisting of all isotropic lines).

LetFqbe a finite field withqelements,whereqis a power of an odd primepandn ≥2 be an integer.LetFnq={(a1,a2,...,an) :ai ∈Fq}be then-dimensional row vector space overFq.Denote byei(1≤i ≤n)the row vector inFnqwhoseith coordinate is 1 and all others are 0.For a nonzero vectorα=(a1,...,an)∈Fnq,let [α] denote the 1-dimensional subspace ofFnqspanned byα.Sometimes,[α] = [(a1,...,an)] is directly written as [a1,...,an] for simplicity.Since,[α] = [kα] for anyk ∈F?q=Fq {0},the representation of a vertex in the form [α] is not unique.However if we write the vertex in the form [a1,a2,...,an] such that the first (from left) nonzero coordinate is 1,then the representation is unique.A vertex[a1,a2,...,an] written in such way is said with standard form.

For ann×nmatrixM,we denote byMTand|M|the transpose and the determinant ofM,respectively.LetGbe the subgroup ofF?qof all square elements.The index ofGinF?qis 2.ThusF?qis exactly a disjoint union ofGandzG,wherezis an arbitrarily given non-square element inFq.Let (α,β)=αSnβTbe a non-degenerate symmetric bilinear form defined onFnqwith respect to a non-singularn×nsymmetric matrixSnoverFq.A vectorαis called isotropic if (α,α) = 0,otherwise,it is called non-isotropic.If a subspace ofFnqconsists of isotopic vectors,it is said to be total isotropic.

We now define the so-called total orthogonal graphO(Sn,q),with respect to a nonsingularn×nsymmetric matrixSnoverFqin such a way: the vertex set is taken to be all 1-dimensional subspaces (or lines) ofFnq,two lines [α] and [β] are adjacent if and only if (α,β)≠0.Obviously,O(Sn,q) is not a simple graph since for a non-isotropic line [α],[α]～[α].By Theorem 1.23 in[10]we know that ann×nnonsingular symmetric matrix overFqis congruent to diag(In?1,θ),whereIn?1refers to the identity matrix of ordern ?1,andθ= 1 orθ=z.If two non-singular symmetric matricesSnandHnare congruent,that is,Sn=PHnPTfor an invertible matrixP,thenO(Sn,q) is isomorphic toO(Hn,q) under the mapping [α][αP],?[α]∈V(O(Sn,q)).In view of this point,we will directly assume thatSn=InorSn=diag(In?1,z),withza fixed non-square element ofFq.

A similar discussion as Theorem 2.1 in [9] shows thatO(Sn,q) is also a strongly regular graph with parameters

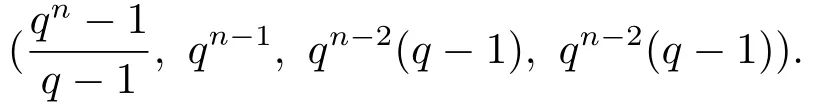
In this paper,the automorphism group ofO(Sn,q) is determined,and the partition ofV(O(Sn,q)) as the union of different orbits is done.

Remark 1.1(i)The three types of isotropic orthogonal graphs studied in[3]are induced subgraphs ofO(Sn,q) with vertices of all isotropic lines.

(ii) For certain unknown reasons,the case when ?is a non-square element ofFqis left by [3] without consideration.However,the orthogonal graphs studied in this paper cover all cases,especially the case whenSnis congruent towhich is left without consideration in [3].

2.Automorphisms of O(Sn,q)

In this section,we determine the automorphism group,denoted by Aut(O(Sn,q)),ofO(Sn,q).Some standard automorphisms are constructed firstly.Based on them every automorphism ofO(Sn,q) is described explicitly.Alln×ninvertible matrices overFqforms a group with respect to matrix multiplication,which is called the general linear group of degreenoverFqand is denoted by GLn(Fq).

LetP ∈GLn(Fq).We defineσP:V(O(Sn,q))→V(O(Sn,q)) by [α][αP].Then using a similar proof as that of Proposition 3.1 in [3] we obtain:

Lemma 2.11) LetP ∈GLn(Fq).ThenσPis an automorphism ofO(Sn,q) if and only if PSPT=kSfor somek ∈F?q.

2) ForP1,P2∈GLn(Fq),σP1=σP2if and only ifP1=kP2for somek ∈F?q.

IfP ∈GLn(Fq) satisfiesPSnPT=kSnfor somek ∈F?qwe callPa generalized orthogonal matrix.All generalized orthogonal matrices of ordernwith respect toSnforms a subgroup of GLn(Fq),called the generalized orthogonal group of degreenoverFqand denoted by GOn(Fq).The center of GOn(Fq) consists of allkEnwithk ∈F?q.The factor group of GOn(Fq) with respect to its center is called the projective generalized orthogonal group of degreenoverFqand is denoted by PGOn(Fq).According to Lemma 2.1,PGOn(Fq) can be viewed as a subgroup of Aut(O(Sn,q)).

Letn= 2,and supposeπis a bijective mapping onFqsatisfyingπ(?x?1θ?1) =?θ?1π(x)?1for anyx ∈F?qandπ(0) = 0.DefineσπfromV(O(S2,q)) to itself by sending each vertex [a1,a2],with the standard form,to [a1,π(a2)].

Lemma 2.2σπis an automorphism ofO(S2,q).

ProofEach vertex [α] is written in the standard form.Obviously,σπis a bijective mapping onV(O(S2,q)).Suppose that [α] = [a1,a2][b1,b2] = [β].Equivalently,a1b1+θa2b2= 0.Ifa1= 0,thena2=b1= 1 andb2= 0.Clearly,σπ([α])σπ([β]).Ifb1= 0,the result is similar.Now suppose that botha1andb1are 1.Thusb2=?θ?1a?12.By the hypothesis forπ,we haveπ(b2) =π(?θ?1a?12) =?θ?1π(a2)?1,which follows that 1+π(a2)π(b2)θ= 0,showing thatσπ([α])σπ([β]).Consequently,[α][β]?σπ([α])σπ([β]).It follows thatd(σπ([α]))≤d([α])for any vertex[α],whered([α])denotes the degree of [α].By

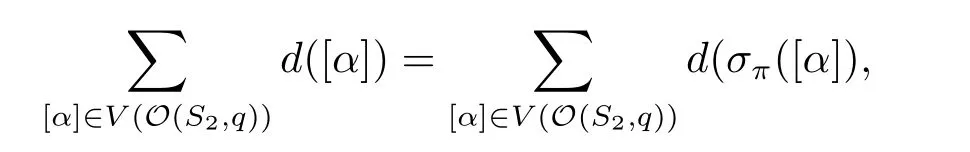
we haved(σπ([α]))=d([α]) for any vertex [α].Then we conclude that [α]～[β]?σπ([α])～σπ([β]).Thus,σπis an automorphism.

Remark 2.1The bijective mappingπonFq,for whichπ(?x?1θ?1)=?θ?1π(x)?1andπ(0)=0,needs not to be an automorphism ofFq.For example,letFqbe the field Z/3Z,and letθ=.Defineπon Z/3Z by fixing,permutingand.Thenπ(?x?1) =?π(x)?1forx=1 and 2.But clearly,πis not an automorphism of Z/3Z.

Forn ≥3,letπbe an automorphism of the fieldFqand letSn= diag(In?1,θ) withθ= 1 orz.Ifθ=z,thenπ(z)/∈F2qandz?1π(z)∈F2q.Supposer ∈F?qsuch thatπ(z) =zr2.Lety=rifθ=z,and lety= 1 ifθ= 1.Then,π(θ) =θy2.Defineσπ,y:V(O(Sn,q))→V(O(Sn,q)) by

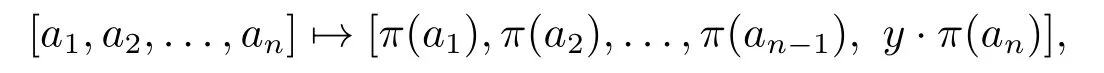
where [a1,a2,...,an] is written in the standard form.

Lemma 2.3σπ,yis an automorphism ofO(Sn,q).

ProofObviously,σπ,yis a bijective mapping onV(O(Sn,q)).The following derivation shows thatσπ,ypreserves adjacency relation of vertices in both directions.

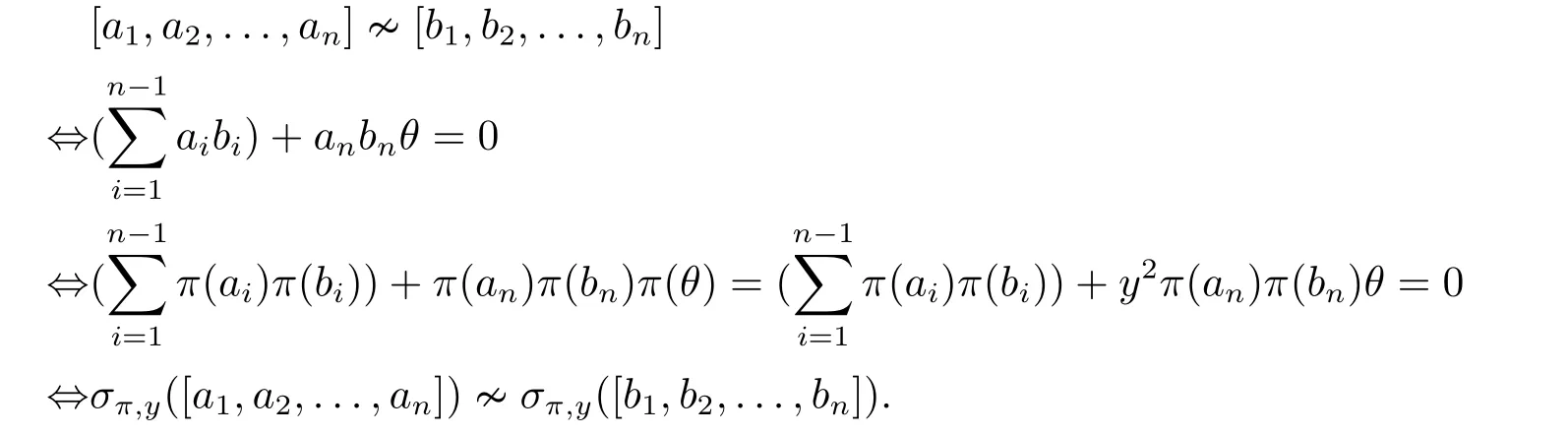
Hence,σπ,yis an automorphism ofO(Sn,q).

Letω= (w1,w2,...,wn)∈ Fnq,wherew2i= 1 for eachiandw1= 1.We defineσωfromV(O(Sn,q)) to itself by sending any [a1,a2,...,an],with standard form,to[w1a1,w2a2,...,wnan].

Lemma 2.4σωis an automorphism ofO(Sn,q).

ProofObviously,σωis a bijective mapping onV(O(Sn,q)).The procedure

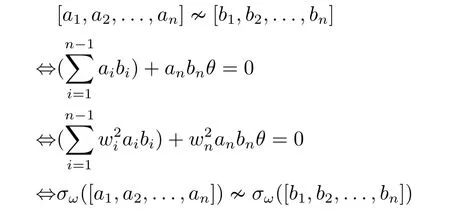
shows thatσωpreserves adjacency relation of vertices in both directions.Thus the result follows.

With the known automorphisms in hands,we now describe every automorphism ofO(Sn,q).Letn ≥3 and let a ={α1,α2,...,αn}be a non-isotropic orthogonal basis ofFnq,and suppose that (αi,αi) =a≠ 0 fori= 1,2,...,n ?1 and (αn,αn) =b≠ 0.Letσbe an automorphism ofO(Sn,q).Assumeσ([αi]) = [βi],and assume (βi,βi) =ci.Thenci≠0 fori= 1,2,...,nand (βi,βj) = 0 fori≠j.Namely,{β1,β2,...,βn}also forms a non-isotropic orthogonal basis ofFnq.For a nonzero vectorsuppose thatIt is easy to see thatbi≠0 if and only ifai≠0.Indeed,ifai≠0,then [α]～[αi].Applyingσ,we havewhich leads tobici≠0.Thusbi≠0.Similarly,bi≠0 impliesai≠0.Sinceσis a bijection fromV(O(Sn,q)) to itself,we define permutationsπi,i=2,3,...,nonFqsuch that

It seems more accurate if one likes to use the symbolπi,σ,ainstead ofπi,as the definition ofπidepends onσand a.

Next,we useπito characterizeσand give some properties forπiandci.

Lemma 2.5(i){β1,β2,...,βn}forms a non-isotropic orthogonal basis ofFnq;

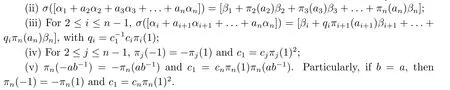
Proof(i) was proved just before this lemma.Assume thatσ([α1+n i=2aiαi]) =Denotebyα,andTo complete the proof of (ii) we need to show thatbi=πi(ai) for eachi ≥2.The case whenai= 0 is trivial.Assume thatai≠0.For the case when 2≤i ≤n ?1,bywe havewhich follows thatThus

On the other hand,by applyingσtowe havewhich leads to

Comparing (2.1) and (2.2),we havebi=πi(ai).Next,we consider the case wheni=n.Applyingσto [α][α1?ab?1a?1n αn],we obtain [β][β1+πn(?ab?1a?1n)βn],which follows thatc1+bnπn(?ab?1a?1n)cn=0.Thus

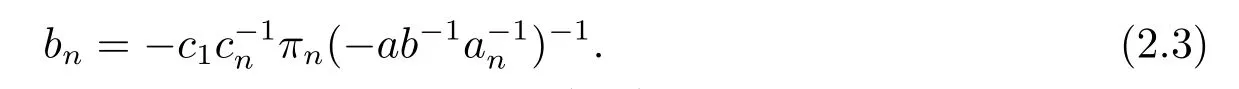
On the other hand,by applyingσto[α1+anαn][α1?ab?1a?1n αn]we have[β1+πn(an)βn][β1+πn(?ab?1a?1n)βn],which follows that

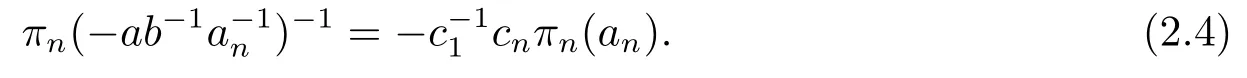
Comparing (2.3) and (2.4),we also havebn=πn(an).The discussions above say that for anya2,a3,...,an ∈Fq,

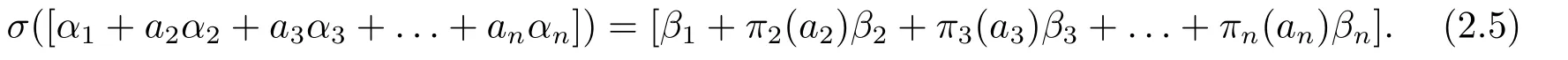
This completes the proof of (ii).

Let 2≤i ≤n ?1 and denoteαi+ai+1αi+1+...+anαnalso byα.Assume that

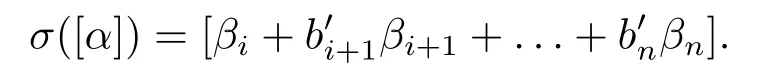
To complete the proof of (iii) we need to show thatb′j=c?11ciπi(1)πj(aj) fori+1≤j ≤n.Denoteβi+b′i+1βi+1+...+b′nβnalso byβ.For the case wheni+1≤j ≤n ?1,applyingσto [α][α1+αi ?a?1j αj] we have

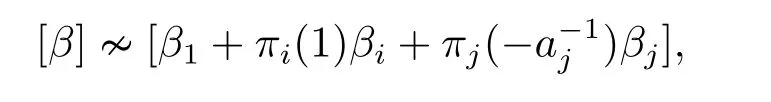
which leads to

Following from (2.2) and (2.6),we obtainb′j=c?11ciπi(1)πj(aj).For the case whenj=n,applyingσto [α][α1+αi ?ab?1a?1n αj] we have

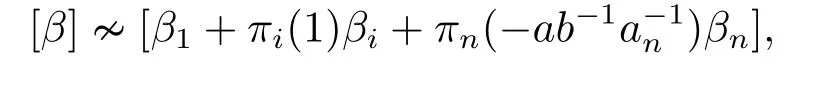
which leads to

From (2.4) and (2.7) we obtainb′n=c?11ciπi(1)πn(an).Thus,

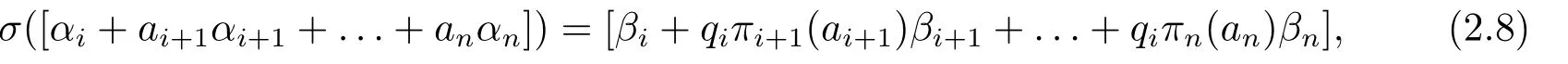
withqi=c?11ciπi(1),which completes the proof of (iii).

Now we are in a position to complete the proof of (iv).Considering the action ofσon[α2+αn][α2?ab?1αn],we have

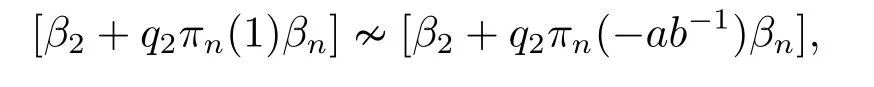
which follows that

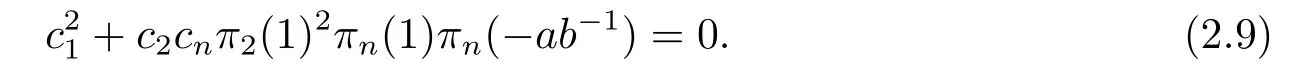
Applyingσto [α1+α2+αn][α2?ab?1αn] we have

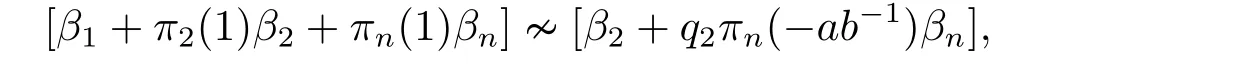
leading to

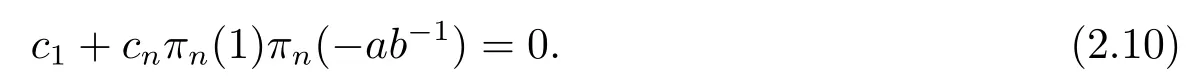
Comparing (2.9) and (2.10),we have that

Applyingσto [α1+α2][α1?α2] we have

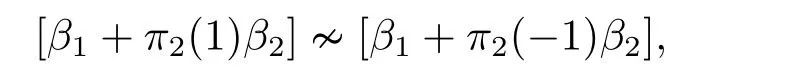
which implies that

From (2.11) and (2.12) we have

Ifn=3,then the proof of(iv)is completed.Ifn ≥4,applyingσto[α1?α2+αj][α2+αj]for 3≤j ≤n ?1,we have

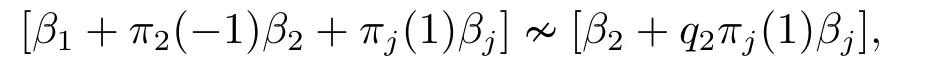
which shows that

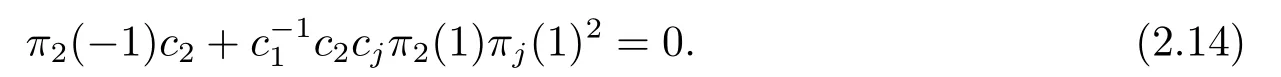
Recalling thatπ2(?1)=?π2(1),we obtain

On the other hand,the action ofσon [α1+α2+αj][α2?αj] leads to

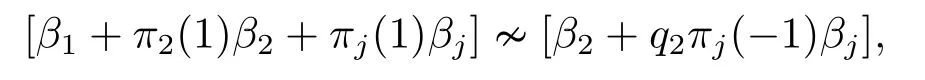
showing that

(2.15) and (2.16) imply that

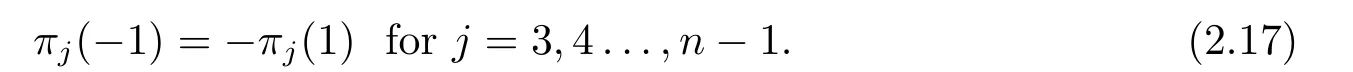
The first assertion of (iv) is confirmed by (2.13) together with (2.17),and the second one is confirmed by (2.11) together with (2.15).

For the proof of (v),considering the action ofσon [α1?α2+αn][α2+ab?1αn],we have

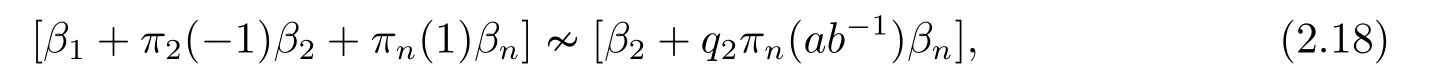
which implies that

Comparing (2.10) with (2.19),we have

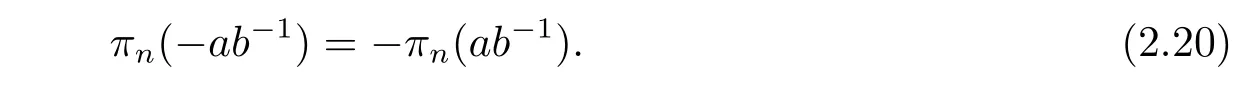
The proof of (v) is completed.

Lemma 2.6Letσ,a,b,πibe defined as in Lemma 2.3.Ifσ([αi])=[αi] for all values ofi,then the following assertions hold.

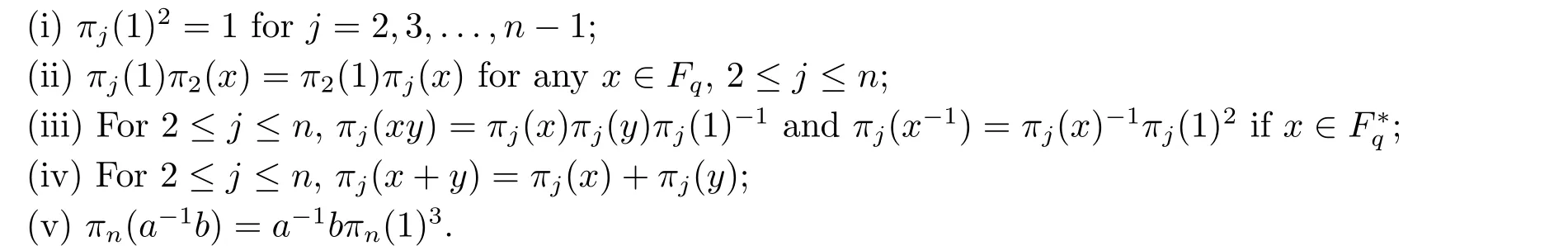
ProofBy (iv) of Lemma 2.3,assertion (i) of this lemma is obvious.

Forx ∈Fqand 2≤j ≤n ?1,applyingσto [α1+xα2+xαj][α2?αj],we have[α1+π2(x)α2+πj(x)αj][α2+π2(1)πj(?1)αj],which leads toπ2(x) =π2(1)πj(1)πj(x).Sinceπj(1)2=1,we have

For the case whenj=n,applyingσto [α1+xα2+xαn][α2?ab?1αn],we have [α1+π2(x)α2+πn(x)αn][α2+π2(1)πn(?ab?1)αn],which leads to

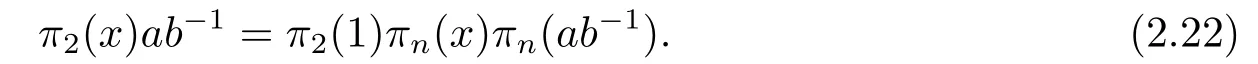
By takingx=1,(2.22) becomes

Substituting this equation into (2.22),we have that

(2.21) and (2.24) together confirm (ii).

Now we prove (iii).Ifxy=0,the result is obvious.Suppose thatxy≠0.By [α1+α2+ab?1xαn][α2?x?1αn] we have [α1+π2(1)α2+πn(ab?1x)αn][α2+π2(1)πn(?x?1)αn],which follows that

Applyingσto [α1+xyα2+yαn][α2?ab?1xαn] we have that

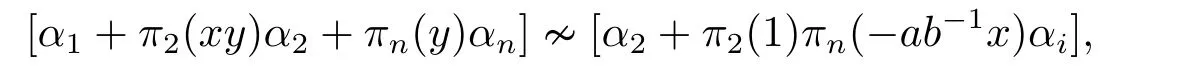
which implies that

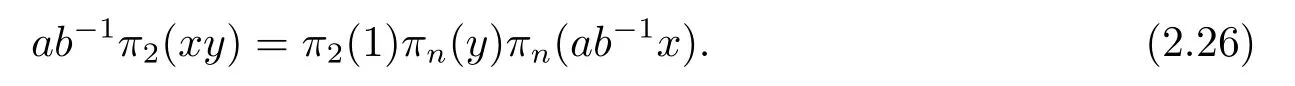
Substituting (2.25) into (2.26),we obtain

Multiplying two sides of (2.27) byπ2(1) and using the result of (ii),we have

Replacingywithxy,andxwithx?1,then we have

Multiplying two sides of (2.29) byπj(1)2and using the result of (ii),we have

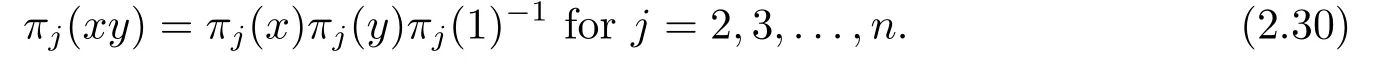
By (2.30),we easily obtain

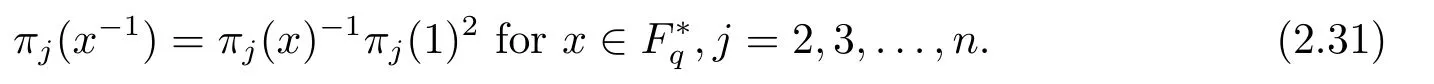
The proof of (iii) is completed.

For the proof of (iv),the case wheny=0 is trivial.Suppose thaty≠0.Applyingσto[α1?(x+y)α2+xαn][α1+y?1α2+ab?1y?1αn] we have

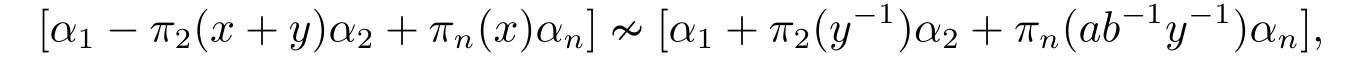
which leads toa ?π2(x+y)π2(y?1)a+πn(x)πn(ab?1y?1)b=0.Or equivalently,

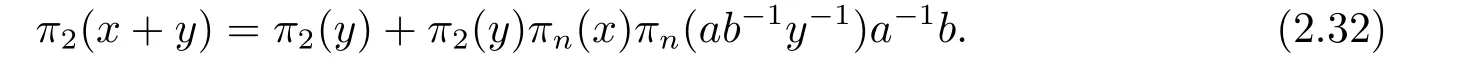
Multiplying two sides of (2.32) byπn(1),we have

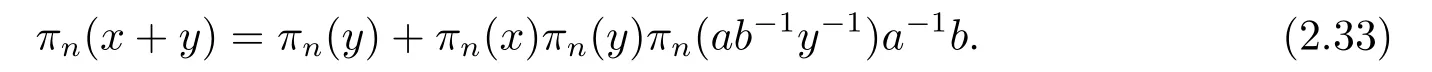
By(iii)of this lemma and(v)of Lemma 2.5,πn(y)πn(ab?1y?1)a?1b=πn(ab?1)πn(1)a?1b=1.Thus (2.33) becomes

By multiplying two sides of (2.34) byπ2(1),it follows that

Finally,multiplying two sides of (2.35) byπj(1),we have

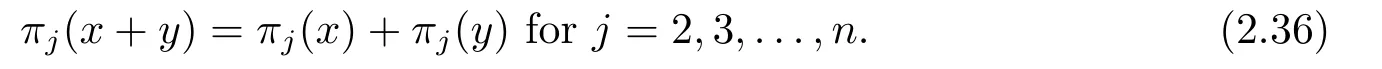
The proof of (iv) is completed.

It follows from (v) of Lemma 2.5 thatab?1=πn(1)πn(ab?1).(iii) of this lemma shows thatπn(ab?1)=πn(a?1b)?1πn(1)2.Consequently,πn(a?1b)=a?1b·πn(1)3.

Now,we are in position to announce the main result of this paper.

Theorem 2.1(i) Ifn= 2,thenσis an automorphism ofO(S2,q) if and only if there exists someK ∈GOn(Fq) and a bijective mappingπonFq,fixing 0 and satisfyingπ(?x?1θ?1)=?θ?1π(x)?1,such thatσ=σK ·σπ.

(ii) Ifn ≥3,thenσis an automorphism ofO(Sn,q) if and only ifσ=σK ·σω ·σπ,y,whereπis an automorphism of the fieldFqsuch thatπ(θ)=y2θ,ω=(w1,w2,...,wn)∈Fnqwithw2i=1,K ∈GOn(Fq).

ProofLetn= 2.Lemma 2.1 and 2.2 together confirm the sufficiency of (i).For necessity,letσbe an automorphism ofO(S2,q),and assumeσ([ei])=[fi] fori=1,2.Let

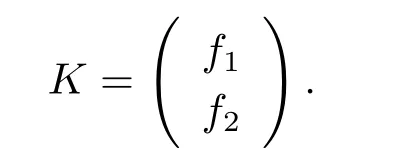
ThenKS2KT= diag(c1,c2),whereci= (fi,fi) =fiS2fTi.Ifθ=z,we havez|K|2=c1c2.Thus only one ofciis a square element,sayc1.By replacingfiwith suitable multiple we may assume thatc1=1 andc2=z.Thus,KS2KT=S2,showing thatK,K?1∈GOn(Fq).ThusσKandσK?1are automorphisms ofO(S2,q).FromKK?1=I2,it follows thatfiK?1=ei.Thus,(σK?1·σ)([ei]) =σK?1([fi]) = [fiK?1] = [ei] fori= 1,2.Ifc2is a square element,similarly,by replacingfiwith suitable multiple we may assume thatc1=zandc2=z2.ByKS2KT=zS2,we also haveK,K?1∈GO2(Fq).Similarly,we know thatσK?1·σfixes [e1]and [e2].Ifθ= 1,by similar discussions as above,we can choose someK ∈GOn(Fq) such that (σK?1·σ)([ei])=[ei] fori=1,2.The procedure is omitted.

Now,letσ1=σK?1·σ.For [α] = [1,x]∈V(O(S2,q)),the first coordinate ofσ1([α])cannot be zero sinceσ1fixes[e1].Thus,we can define a mappingπonFqsuch thatσ1([1,x])=[1,π(x)].Obviously,πis bijective andπ(0) = 0.Forx≠ 0,by applyingσ1to [1,x][1,?x?1θ?1],we have [1,π(x)][1,π(?x?1θ?1)],which leads to 1+θπ(x)π(?x?1θ?1) = 0,showing thatπ(?x?1θ?1) =?θ?1π(x)?1.Thusπcan be used to define the automorphismσπofO(S2,q).Clearly,σ1([α])=σπ([α]) for each [α]∈V(O(S2,q)),with the standard form.Finally,we haveσ1=σπandσ=σK ·σπ.

For the proof of (ii),sufficiency is obvious.Now we consider necessity.Letσbe an automorphism ofO(Sn,q).Obviously,(ei,ei) =eiSeTi= 1 fori= 1,2,...,n ?1,(en,en) =enSeTn=θand (ei,ej) = 0 fori≠j.Thus,a ={e1,e2,...,en}forms a non-isotropic orthogonal basis ofFnq.Assume thatσ([ei])=[fi] and (fi,fi)=ci.Let

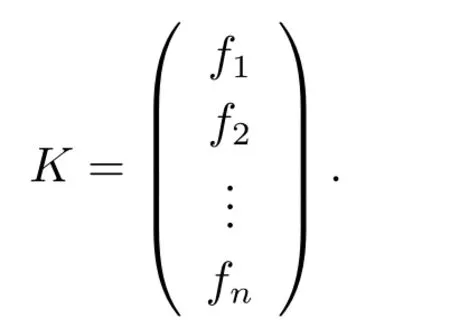
ThenKSKT= diag(c1,c2,...,cn).As what we did just before Lemma 2.3,we define the permutationsπi(i=2,3,...,n),with respect toσand a,onFqsuch that

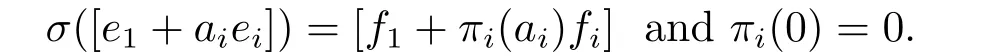
By Lemma 2.3,we havecj=c1πj(1)?2forj=2,3,...,n ?1,andcn=c1πn(1)?1πn(θ?1)?1.

Setπ1(1)=1 andπ1(0)=0.Letfi′=πi(1)fifori=1,2,...,n,and let

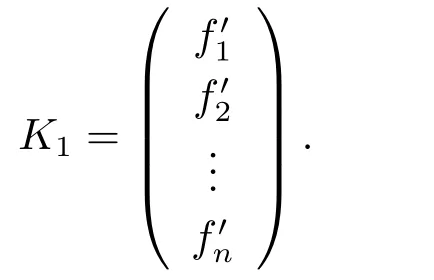
Then we also haveσ([ei])=[f′i],however

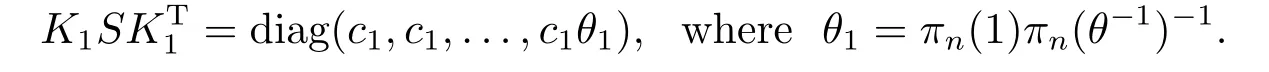
For simplity,f′iis also written asfiandK1is also written asK.

Now we consider the case whenθ= 1.ThenS=InandKKT=c1In.ThusK,K?1∈GOn(Fq),andσK,σK?1∈Aut(O(Sn,q)).It follows fromKK?1=InthatfiK?1=eifori=1,2,...,n.Thus,(σK?1·σ)([ei])=σK?1([fi])=[fiK?1]=[ei]for eachi.DenoteσK?1·σbyσ1.Thenσ1fixes each [ei].Define permutationsπi,with respect toσ1and a,onFqsuch that

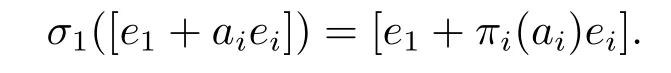
Let 0≠α ∈Fnq.We write [α] in the standard form [α]=[a1,a2,...,an].Then by using (ii)and (iii) of Lemma 2.3 and recalling thatπi(1)2=1 for 1≤i ≤n,we have

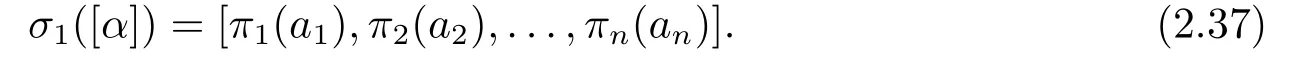
DefineπonFqbyπ(x) =π2(1)?1π2(x) forx ∈Fq.Sinceπi(1)?1πi(x) =π2(1)?1π2(x) fori= 3,4,...,n,we knowπ=πi(1)?1πifor eachi(≥2).By (iii) and (iv) of Lemma 2.6,it is easy to see thatπ(xy)=π(x)π(y) andπ(x+y)=π(x)+π(y) for allx,y ∈Fq,showing thatπis an automorphism ofFq.Now,(2.37) becomes

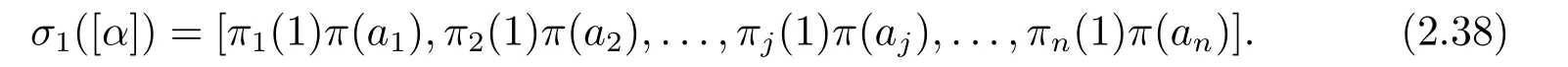
Letω=(π1(1),π2(1),...,πn(1)).Sinceπi(1)2=1 for eachi(thanks to(iv)and(v)of Lemma 2.3),we can useωto define the automorphismσωofO(Sn,q).Now,

This equation shows thatσω·σ1=σπ,1.Finally,we haveσ=σK ·σω·σπ,1.

For the left caseθ=z(a fixed non-square element inFq),KSKT=diag(c1,c1,...,c1θ1)withθ1=πn(1)πn(z?1)?1.We claim thatθ1cannot be a square element.Otherwise,sayθ1=r2.By replacingfnwithr?1fn,we haveKSKT=diag(c1,c1,...,c1).Thus(fi,fi)=c1for alli.Sinceσ?1([fi])=[ei] for eachi,applying (v) of Lemma 2.3 toσ?1(viewingfiasαiand viewingeiasβi),we have that 1=(e1,e1)=(en,en)πn(1)2=zπn(1)2,absurd.So we may assume thatθ1=zs2.Replacingfnbys?1fn,we have thatKSKT=diag(c1,c1,...,c1z)=c1S.ThusK?1is a generalized orthogonal matrix.UsingK?1we define the automorphismσK?1onO(Sn,q) and denoteσK?1· σbyσ1.Similar as the case whenθ= 1,we haveσ1([ei])=σK?1([fi])=[fiK?1]=[ei] for eachi.

Define permutationsπi,with respect toσ1and a,onFqsuch that

Then by (ii) and (iii) of Lemma 2.3,

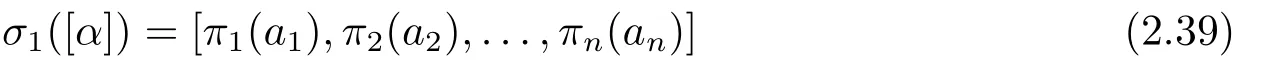
for [α]∈V(O(Sn,q)) with standard form,whereπ1fixes 1 and 0.DefineπonFqbyπ(x)=π2(1)?1π2(x)forx ∈Fq.Also,πis an automorphism ofFq,andπ=πi(1)?1πifor eachi(≥2).Now,(2.39) becomes

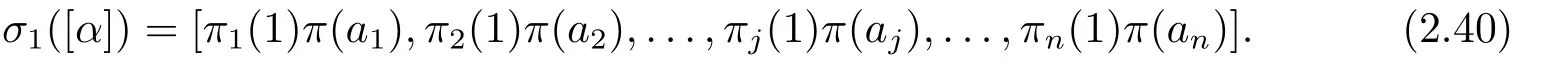
Letω=(π1(1),π2(1),...,πn?1(1),1).By(i)of Lemma 2.4,πi(1)2=1 for each 1≤i ≤n?1.So we can useωto construct the automorphismσωofO(Sn,q).Then

Lety=πn(1).(v) of Lemma 2.4 shows thatπ(z) =πn(1)?1πn(z) =y2z.Thus we can useπandyto define the automorphismσπ,yofO(Sn,q).It is easy to see thatσω ·σ1=σπ,y.Finally,σ=σK ·σω·σπ,y,as desired.

3.Orbits Partition of V(O(Sn,q)) Under the Automorphisms

The study of orbits partition ofV(O(Sn,q)) needs an elementary lemma on GOn(Fq).

Lemma 3.1LetSn= diag(In?1,θ) withθ= 1 orz.Ifnis odd,then for eachK ∈GOn(Fq) withKSnKT=kSn,kmust be a square element.Ifnis even,then there existsK ∈GOn(Fq) such thatKSnKT=zSn.

ProofLetnbe odd,and supposeK ∈GOn(Fq) such thatKSnKT=kSn.Thenθ|K|2=knθ,showing thatkn=|K|2,andkis a square element.Now,assume thatnis even.A well known result about finite fields is that the equationX2+Y2=zhas solutions inFq.Suppose thata,b ∈Fqsuch thata2+b2=z.Ifθ=1,for 1≤2k+1<2k+2≤n,set

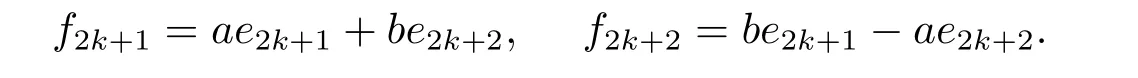
Ifθ=z,we set

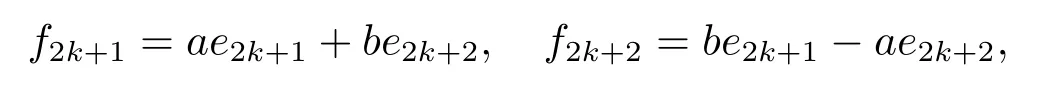
for 1≤2k+1<2k+2≤n ?2,and setfn?1=en,fn=zen?1.Let

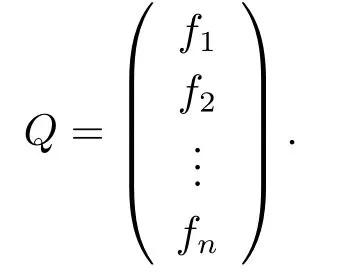
Then,we haveQSnQT=zSn.LetV0be the subset ofV(O(Sn,q)) of all isotropic lines and let

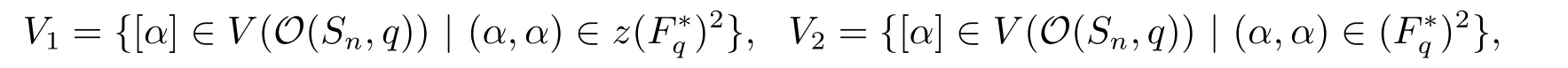
where (F?q)2refers the set of all non-zero square element ofFq.

Theorem 3.1Ifnis odd,thenV(O(Sn,q)) has three orbits,they areV0,V1andV2.Ifnis even,thenV(O(Sn,q)) has only two orbits,they areV0andV1∪V2.

ProofFor [α],[β]∈V(O(Sn,q)),if they belong to the sameVi,then by replacingαwith its suitable multiple we may assume that (α,α) = (β,β).Using Lemma 6.8 in [10],we can find an orthogonal matrixQsuch thatαQ=β.ThusσQ([α]) = [β],showing that all elements lying in the sameVibelong to one orbit.If [α]∈V0,clearly,σ([α])∈V0for allσ ∈Aut(O(Sn,q)).It implies thatV0forms an orbit.

Ifnis odd,we want to prove thatV2is stable under the action of Aut(O(Sn,q)).Let[α]=[a1,a2,...,an]∈V2(with the standard form),and letσbe an automorphism ofO(Sn,q).We consider the action ofσon[α].By Theorem 2.1,σcan be decomposed asσ=σK·σω·σπ,y,whereK ∈GOn(Fq) withKSnKT=kSn,ω= (w1,w2,...,wn)∈Fnqwithw1= 1 andw2i= 1,andπis an automorphism ofFqsatisfyingπ(θ) =θy2fory ∈Fq.Assume thatσ([α])=[β].Then,

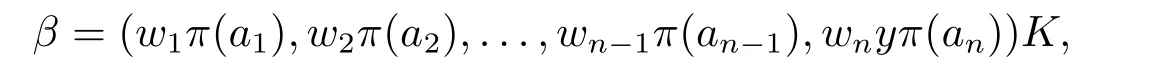
and

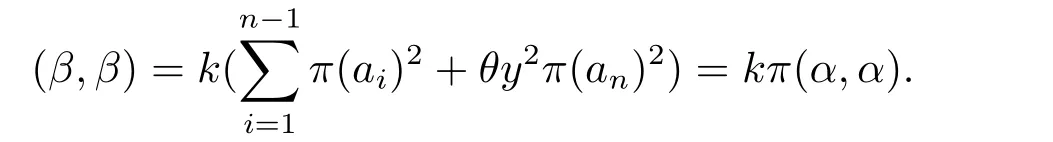
Since (α,α)∈(F?q)2,it follows thatπ(α,α)∈(F?q)2.By Lemma 3.1,k ∈(F?q)2,thusσ([α])=[β]∈V2.It implies thatV2forms an orbit,which immediately follows thatV1forms an orbit.

Ifnis even,by Lemma 3.1,we can chooseQ ∈GOn(Fq) such thatQSnQT=zSn.Then for [α]∈V2,we have [αQ]∈V1sinceαQSnQTαT=z(α,α)∈z(F?q)2.Consequently,σQ([α])=[αQ]∈V1.It follows thatV1∪V2forms an orbit.