(山東師范大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,250358, 濟(jì)南)

1 引 言

本文考慮一個(gè)重要的半?yún)?shù)模型—變系數(shù)部分非線性模型, 其模型形式為:

Y=ZTα(U)+g(X;β)+ε,

(1)

其中α(·)=(α1(·),...,αp(·))T是未知系數(shù)函數(shù)的p維向量,g(·;·)是預(yù)先指定的函數(shù),β是未知參數(shù)函數(shù)的d維向量,ε是獨(dú)立于(ZT,U,XT)T的隨機(jī)誤差并且E(ε)=0.

近年來(lái), 關(guān)于變系數(shù)部分非線性模型的統(tǒng)計(jì)推斷得到廣泛關(guān)注. 例如, 文獻(xiàn)[1]提出了一種輪廓非線性最小二乘估計(jì), 并進(jìn)一步引入了廣義似然比檢驗(yàn), 去檢驗(yàn)?zāi)Ｐ椭械淖兿禂?shù)是否為常數(shù). 文獻(xiàn)[2]提出了兩階段估計(jì)程序, 他們首先基于正交投影方法去估計(jì)參數(shù)系數(shù), 然后用B樣條基函數(shù)逼近每一個(gè)變系數(shù)函數(shù). 文獻(xiàn)[3]應(yīng)用似然方法去推斷參數(shù)和非參數(shù)部分. 但是這些方法都是基于最小二乘方法提出的, 對(duì)異常值非常敏感. 最近, 文獻(xiàn)[4]基于指數(shù)平方損失對(duì)一般線性模型進(jìn)行一系列的穩(wěn)健估計(jì), 證明了所提出的估計(jì)方法不僅能保持高穩(wěn)健性, 而且在正態(tài)誤差條件下, 與無(wú)異常值的最小二乘方法一樣, 得到很好的估計(jì)結(jié)果. 文獻(xiàn)[5]對(duì)變系數(shù)部分非線性模型應(yīng)用指數(shù)平方損失方法進(jìn)行估計(jì), 它們對(duì)變系數(shù)部分進(jìn)行局部多項(xiàng)式展開(kāi), 分兩步進(jìn)行估計(jì), 并提出新的MM算法去計(jì)算非參數(shù)和參數(shù)部分的估計(jì), 得到不錯(cuò)的結(jié)果. 但是分兩步估計(jì), 計(jì)算量很大.

在本文中, 受文獻(xiàn)[4]和文獻(xiàn)[5]的啟發(fā), 我們對(duì)模型(1)也使用指數(shù)平方損失方法, 對(duì)未知參數(shù)進(jìn)行穩(wěn)健估計(jì), 但是我們對(duì)變系數(shù)部分采取B樣條基函數(shù)逼近的方式展開(kāi), 這樣變系數(shù)部分可以寫(xiě)成線性組合表示的形式, 便于計(jì)算和估計(jì). 并在一定正則條件下, 建立了估計(jì)量的漸近性質(zhì).

2 估計(jì)方法

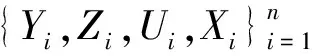
(2)

其中h是調(diào)節(jié)參數(shù), 它控制著估計(jì)的穩(wěn)健性和有效性.

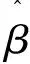
(3)

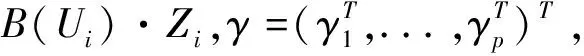
3 估計(jì)的漸近性質(zhì)

為了建立所提估計(jì)的漸近性質(zhì), 本文提出以下正則條件, 其中C表示正常數(shù), ‖·‖代表2-范數(shù).

條件1 指示變量U有有界支撐Ω并且它的密度函數(shù)fU(·)是正的, 還有連續(xù)的二階導(dǎo)數(shù), 不失一般性, 我們假設(shè)Ω是單位間隔[0,1].

條件2 變系數(shù)函數(shù)α1(u),...,αp(u)在[0,1]上是r次連續(xù)可微的, 并且r>2.

條件3 令Σ1(u)=E{ZZT|U=u},Σ2(u)=E{g′(X;β)g′(X;β)T|U=u}關(guān)于u是連續(xù)的, 此外, 對(duì)于給定的u, Σ1(u)和Σ2(u) 是正定矩陣, 并且他們的特征值是有界的, 除此之外, 假設(shè)

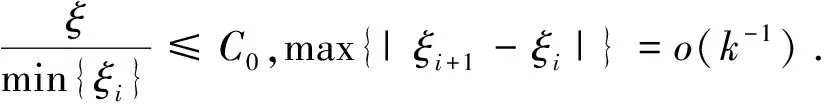
條件5F(z,x,u,h)和G(z,x,u,h)關(guān)于(z,x,u)是連續(xù)的.

條件6 對(duì)任意的h>0, 都有F(z,x,u,h)<0.

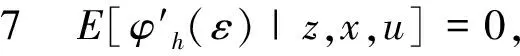
條件8g(·;β)是關(guān)于β的連續(xù)函數(shù),g(·;β)關(guān)于β的二階導(dǎo)存在并且連續(xù).

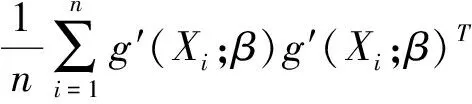
記α0(·)和β0分別是α(·)和β的真實(shí)值, 有下面的定理1和定理2成立.

定理1 假設(shè)正則條件1至條件6成立, 并且k=O(n1/(2r+1)), 那么我們有

定理2 假設(shè)正則條件1至條件8成立, 并且k=O(n1/(2r+1)), 那么我們有

其中定理和定理證明中所使用的符號(hào)表示如下：

4 估計(jì)性質(zhì)的證明

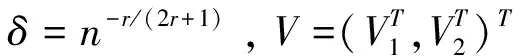
我們首先證明, 對(duì)于任意給定的η>0, 存在C使得

(4)

通過(guò)泰勒展開(kāi), 我們有

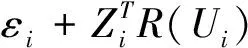
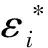
類(lèi)似的我們能得到I3=Op(nδ3k-1‖V‖3), 因?yàn)棣?n-r/(2r+1)→0, 當(dāng)‖V‖=C時(shí),δ‖V‖→0.因此,I3也被I2控制住.

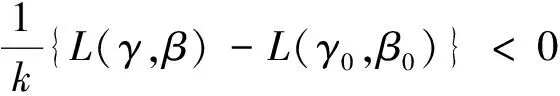
(5)

定理1的結(jié)論(1)證明完成, 下面證明定理1的結(jié)論(2).

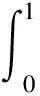
4.2定理2的證明在定理1的證明中可以看到, 當(dāng)n→時(shí), 概率趨于1. (3)式中的l(γ,β)在和處獲得最大值, 通過(guò)計(jì)算, 我們有

通過(guò)簡(jiǎn)單的計(jì)算及泰勒展開(kāi), 有

(6)

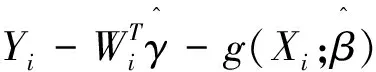
類(lèi)似地,有

(7)

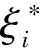
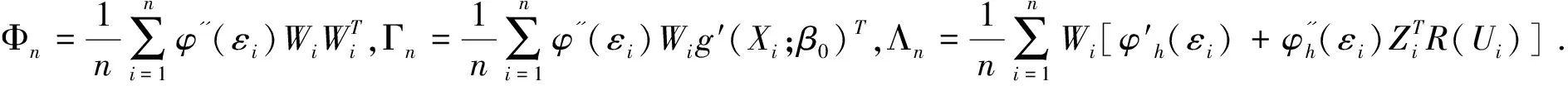
那么, 根據(jù)正則條件3和條件7, 基于等式(7), 經(jīng)過(guò)計(jì)算有

(8)

將式(8)代入式(6)中, 我們得到

注意到

通過(guò)(8)很容易得到

(9)

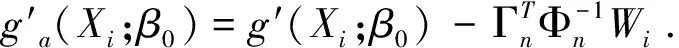
利用大數(shù)定律, 有

(10)

利用中心極限定理, 有

(11)

聯(lián)合(10)和(11), 應(yīng)用Slutsky定理, 有

定理2證明完成.