QIAN Guangming,SU Shen

(College of Information Science and Engineering,Hunan Normal University,Changsha 410081,China)

【Abstract】 In a periodic real-time system scheduled with the Earliest Deadline First (EDF) algorithm,it is necessary to compress some current tasks to avoid overloading if new task requests to run.Compressing a task means that its period is prolonged while its computation time keeps unchanged.An interesting problem is to find the earliest time to release new tasks without any deadline missing,that is,the earliest smooth insertion time.In this paper,a general frame to calculate the earliest time with multiple rounds of deadline checking is given,which shows that the checking can be done from the request time of the new tasks.A smart way is provided and proved,which takes the value of the Δ checking of the current round as the time step to the next.These techniques potentially reduce the amount of the calculation and the number of the rounds of the checking to get the earliest time.Simulation results are also given to support the conclusion.

【Key words】 total utilization;new tasks insertion;simple way;smart way;Δ checking

0 Summary

Many real-time systems often schedule tasks adaptively with the load[1-2].In this paper,the load refers to the sum of the utilizations (or bandwidths) of all the tasks in the system,that is,the total utilization.

A light load system may operate at low frequency to save energy,or even sleep[3-4].As the load becomes heavier,the operating frequency should probably be increased to meet the timing constraints of the tasks in the system.Consider a heavy load system scheduled with the Earliest Deadline First (EDF) algorithm[5].If some new bandwidth requirements arrive,then the total utilization may be greater than one and the system will become overloaded and unschedulable even if the working frequency is increased.A possible way to avoid overloading is to compress some current tasks,that is,to decrease their utilizations[1].

The new bandwidth requirements may be some current tasks’ acceleration and/or new tasks’ insertion into the current task set[6].Some application scenarios are described in References [1,7],such as the scheduling for robot target approaching.A task’s acceleration means that its period is decreased while the computation time keeps unchanged.It is proved that the acceleration of a current task can be treated as the insertion of an equivalent new task[6].Therefore,as for as new bandwidth requirements,new tasks’ insertion (or insertion for short) is discussed only.

The problem of the insertion belongs to a kind of mode-change problem[8-10].It has three stages:the old mode starting fromtoldb,the transition process fromtrand the new mode fromtnewb.tris the time point at which the request of the insertion occurs and some current tasks may be compressed.

If new tasks are inserted attrimmediately,it is known that deadline missing may occur even though the total utilization does not exceed one[1,11].In Reference [12],the transition process is reasonably defined,and it is proved that deadline missing is only possible during the transition process [tr,tnewb) if the total utilization is not greater than one.

?t≥tr,tis called a smooth insertion timeδif new tasks are released attwithout any deadline missing afterwards.Obviously,finding the earliest smooth insertion time (denoted byδearliest) is a significant problem.

A simple way to evaluateδearliestis to do multiple rounds of deadline checking,named “Simple way” in the following sections.In this way,first this paper assumesδearliest=trand checks every deadline fromδearliesttotnewb.If deadline missing is not found then it concludes thatδearliestis really equal totrand no more checking is required,otherwise,the next round of checking is needed with

δearliest=δearliest+tstep

(1)

Thetstepin Equation (1) takes one time unit.Similarly,the third round of checking is needed if a missed deadline is asserted from the second round.And so on.Finally,the number of the required rounds to find the realδearliestdepends on the length of the transition process and the number of the deadlines during the transition.

The major contribution of this paper is that a more efficient way to calculateδearliestis provided and proved,named “Smart way” or “Smart try”.Instead of one time unit in the Simple way,thetstepin the Smart way takes the difference of the total processor demand minus the length of the discussed time interval,which is greater than or equal to one time unit.

1 Processor demands after compression

In this section,first the model of tasks’ compression provided in References [12-13] is recalled and improved,then several expressions for evaluating the associated processor demands after compression are presented,which are used to judge whether the deadlines in the transition process are satisfied.

1.1 System model

As in Reference [12],the task modelτx(Cx,Tx) is used in this paper,whereTxis the period andCxrepresents the computation time in each period.

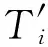
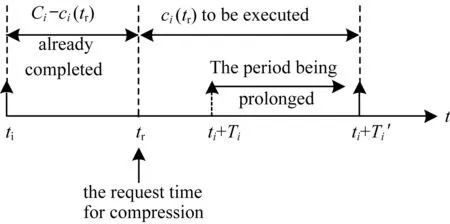
Fig.1 Compression of the task τi

The task setMis compressed for new tasks’ insertion.In the following descriptions,it is supposed that all the new tasks form a subsetJand they are inserted into the system at the same time,the sum of the utilizations of these tasks isUJandrJis introduced to represent the release time of their first instances.Obviously,rJ≥tr.In order to keep the system schedulable in the new mode,UJis not greater than the freed utilization fromM,that is,

(2)

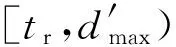
The release pointrJof the first instances of the new tasks may be any time fromtr.The earliestrJthat does not cause any deadline missing isδearliest.The insertion is called an immediate smooth insertion ifδearliest=tr.

1.2 Processor demand calculation

The proof of the theorems below requires the processor demand criterion[14-15].Firstly,some associated symbols and notations are given.

In [t1,t2],the processor demand of the taskτx(Cx,Tx) is labeled withDx(t1,t2).The sum of the processor demands of all the tasks inJandMare indicated withDJ(t1,t2) andDM(t1,t2),respectively.The sum ofDJ(t1,t2) andDM(t1,t2) is called the total processor demandDtotal(t1,t2).

Then,Δ(t1,t2)=Dtotal(t1,t2)-(t2-t1) is introduced.According to the criterion in Reference [14],the deadlines att2are met if and only ifΔ(t1,t2) is less than or equal to zero.Checking whetherΔ(t1,t2) is greater than zero is called “Δchecking” in the following descriptions.

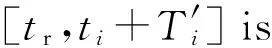
(3)

(4)

The new tasks in the subsetJare released atrJ.?τj(Cj,Tj)∈J,fromrJto any timet,it getsDj(tr,t)=?(t-rJ)/Tj」Cj.Therefore,

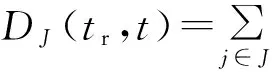
(5)

Based on these expressions,Theorem 1 is given to check whether the deadlines are satisfied (thus calculating the earliest smooth insertion time).

Theorem1With compressing the task setM,supposedxis a deadline during the transition process.Then deadline missing will not occur att=dxif and only if

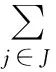
(6)

Di(tr,dx)=

(7)

Proof: In [tr,dx] it gets

Dtotal(tr,dx)=DJ(tr,dx)+DM(tr,dx)=

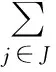
ThenΔchecking is calculated

Δ(tr,dx)=Dtotal(tr,dx)-(dx-tr)

The deadline att=dxis satisfied if and only ifΔ(tr,dx)≤0.Replacingtwithdxin Equation (3)～Equation (5),it is easy to see that Equation (6) and Equation (7) are correct.

Theorem 1 is proved.

2 The Smart way

In order to clearly demonstrate the advantages of the Smart way,it is necessary to pay special attention to the time sequence:

(8)

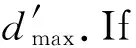
Two features with the Simple way should be noticed:1)Δchecking should be done with every deadline and 2) thetstepis equal to one.

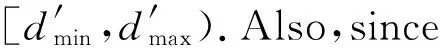
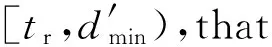
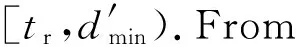
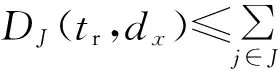
(dx-tr)

Dtotal(tr,dx)=DM(tr,dx)+DJ(tr,dx)≤(dx-tr)

Therefore,

Δ(tr,dx)=Dtotal(tr,dx)-(dx-tr)≤0

This means thatdxmust be met.

Theorem 2 is proved.

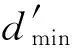
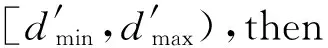
δearliest≥rJ+Δ(tr,tx)

(9)

That is,the delayed insertion becomes possibly smooth only when the release time is delayed by not less than the value of theΔchecking.

Proof: WhenΔchecking is done attx,A1,B1,andC1are caculated as

A1=Dtotal(tr,tx)

B1=DM(tr,tx)

C1=DJ(rJ,tx)

Obviously,A1=B1+C1andΔ(tr,tx)=A1-(tx-tr).

If the value of theΔchecking with this round isΔ(tr,tx)>0,then the release time of the new tasks should be delayed torJ+tstepand the next round of checking is started.It is guessed that thiststepshould be greater than or equal toΔ(tr,tx).

This paper continues the discussion with Case 1 and Case 2.

Case1If there is at least one deadline from the new tasks attx,as shown in Figure 2.

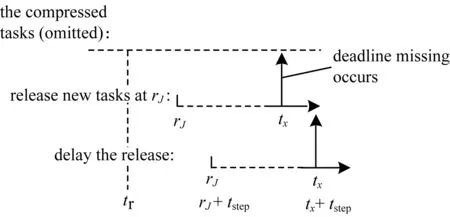
Fig.2 New tasks have at least one deadline at tx

Then,this deadline will shift totx+tstepwith the delaying.Notice that after the delaying,not only the deadlines (if any) attxshould be met,but also the deadlines attx+tstepmust be satisfied.

Let us introduceA2,B2,andC2for this new round of checking after the delaying:

A2=Dtotal(tr,tx+tstep)

B2=DM(tr,tx+tstep)

C2=DJ(rJ+tstep,tx+tstep)

A2=B2+C2

High attention should be paid to the new tasks that haveC2=C1,that is,the processor demand of every new task does not increase tilltx+tstep.However,the old tasks haveB2≥B1,since their processor demands may increase.Thus,the total processor demand of the system is

Dtotal(tr,tx+tstep)=A2=B2+C2≥B1+C1=A1

With this new round of checking,the deadlines attx+tstepare satisfied if and only if theΔchecking value is not greater than zero,that is,

Dtotal(tr,tx+tstep)-(tx+tstep-tr)=

Δ(tr,tx+tstep)≤0

Then,

tstep≥Dtotal(tr,tx+tstep)-(tx-tr)≥A1-(tx-tr)

Here,it should be noticed thatA1-(tx-tr) is theΔchecking value of the previous round.This shows that the minimal value of thiststepis equal to theΔchecking value of the previous round,hence Equation (9) is true.

Case2If no deadline from the new tasks exists attx,as shown in Figure 3.

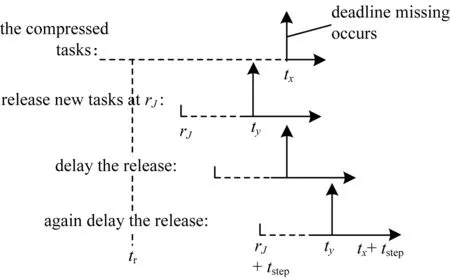
Fig.3 No deadline from new tasks exists at tx

That is to say,the missed deadline attxmust be from some compressed tasks.Suppose that the deadline from the new tasks closest to the left oftxis atty.The release of the new tasks is delayed if theΔchecking value isΔ(tr,tx)>0.The first step delay taken is so that the deadline from the new tasks attymoves totx.However,because the processor demands of the compressed tasks as well as the new tasks remain unchanged in [tr,tx],Δ(tr,tx) keeps the same value as before the delay,and hence further delay has to be done.

Note that it is an exact Case 1 after the first step delay.This implies that with Case 2,the minimal value of itststepis greater than theΔchecking value of the previous round,thus Equation (9) is correct.

Taking Case 1 and Case 2 together,Equation (9) is got.

Theorem 3 is proved.

Theorem 3 indicates that if the release of the new tasks based on this round is unsuccessful,then there must be aΔchecking value greater than zero (at least one time unit).This value can be taken as thetstepto the next round,andtstep≥1.

The Smart way has the advantage that thetstepmay be greater than one.Let us call it “advantage of step”.This paper discusses how many times of theΔchecking can be saved by this advantage in two cases.1) Suppose that the unsatisfied deadlinedxbeing checked is from the compressed tasks.Using the Simple way,dxwill be rechecked after the delay ofrJby one time unit,that is,rJ=rJ+1.However,the Smart way rechecksdxafterrJ=rJ+tstepso that the times of the checks that can be omitted is “tstep-1”.2) Suppose that the unsatisfieddxis from the new tasks.In this case,the next deadlines to be checked after delay with the Simple way and the Smart way aredx+1 anddx+tstep,respectively.Then,the times of the checks saved by the Smart way is also “tstep-1”.

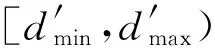
3 Simulations

The Theorems described above are verified by simulation.An illustrative example is shown in Figure 4.The compressed task setMis composed ofτ0(8,16) andτ1(8,16),while the subsetJof the new tasks contains only one taskτ2(2,8).

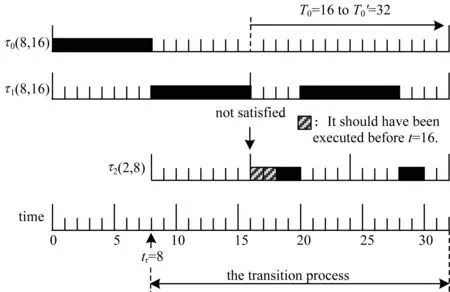
Fig.4 Example of deadline missing after insertion

First lettr=8,then different values oftrare discussed.Here,τ0is compressed while the period ofτ1remains unchanged,and

The remaining computationc0(tr)=0,c1(tr)=8.

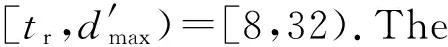
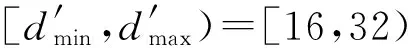
Round 1:

LetrJ=tr=8.The deadlines of the compressed tasks inMis checked.As shown in Figure 4,τ0has no deadline in [16,32),thus the deadline ofτ1att=16 is checked first.

Δ(8,16)=Dtotal(8,16)-(16-8)=

D0(8,16)+D1(8,16)+

D2(8,16)-8=0+8+2-8=2>0

This positive value of theΔchecking means that there is deadline missing att=16.One deadline ofτ2is not satisfied as in Figure 4.

Round 2:

Taking the positive value from Round 1 as thetstep,the release time of the new task is increased torJ=rJ+tstep=8+2=10.Again the deadline ofτ1is checked att=16:

Δ(8,16)=Dtotal(8,16)-(16-8)=

D0(8,16)+D1(8,16)+D2(8,16)-8=

0+8+0-8=0

This indicates that no deadline will be missed att=16.Now the inspection ofMis completed and the check ofJis started.τ2has two deadlines att=18 andt=26,theΔchecking values of them are 0 and -6,respectively.Both are satisfied.

Therefore,the second round of checking draws the conclusion that the system is schedulable.Then the earliest smooth insertion time is

δearliest=10

In this way,δearliestis obtained through 4 times ofΔchecking with 2 rounds.Comparatively,if the Simple way (tstep=1) is used,it is not difficult to find that 3 rounds and 5 times ofΔchecking are necessary:The first round is done withrJ=8,the second round withrJ=9,and the third withrJ=10.

LetNOsmartandNOsimplerepresent the required times ofΔchecking with the Smart way and the Simple way,respectively.Also,the “percentage of reduction”,labeled withPis introduced that

P=(NOsimple-NOsmart)/NOsimple

The greater theP,the greater the advantage of the Smart way has.With the above example,

P=(5-4)/5=20%

In Figure 4,iftr=9 is assumed instead oftr=8,the new task can not be inserted immediately either,and the Smart way or the Simple way is required to getδearliest.The value of the correspondingPis

tr=9,P=(4-4)/4=0%

4 Conclusions

This paper discusses the problem of when new tasks can be inserted smoothly after compressing the task setM,that is,to evaluate the earliest smooth insertion timeδearliest.The main features of the proposed Smart way are as follows:

1) Rather than fromtoldb,Theorem 1 gives the expressions to calculate the processor demands of the tasks fromtrthat is the start of the transition process and is usually later thantoldb.This helps to reduce the amount of calculation.

3) In some cases,δearliestcan be calculated byΔchecking with thetstepgreater than one,thus the number of the rounds and the times of theΔchecking are reduced to reachδearliest.