SONG Jin,XUE Hi-Lend DA Cho-Jiu

aCollege of Sciences,Inner Mongolia University of Technology,Hohhot,China;bState Key Laboratory of Severe Weather,Chinese Academy of Meteorological Sciences,Beijing,China;cSchool of Mathematics and Computer Science Institute,Northwest University for Nationalities,Lanzhou,China

ABSTRACT The propagation of Rossby waves on the Earth’s δ-surface is discussed in a reference frame propagation with the zonal phase speed of the wave.In this reference frame,trajectories and streamlines coincide;the propagation of Rossby waves has a different interpretation than in a reference frame fixed on the ground;and the mechanism for the propagation of Rossby waves depends not only on the different positions of the wave relative to the basic current,but also the variation of β with latitude(called the δ-effect).

KEYWORDS Trajectory;Rossby waves;β-plane;δ-effect

1.Introduction

Rossby waves are a fundamental wave motion in largescale atmospheric and oceanic dynamics,affecting weather and climate.The propagation of Rossby waves is related to the variation in the Coriolis force with latitude,the so-called β-effect.There have been many studies on the subject of Rossby waves.Plazman(1968)and Hoskings,McIntyre,and Robertson(1985)explained the Rossby wave propagation mechanism.Holton and Hakim(2012)showed the mechanism of Rossby wave propagation in a barotropic atmosphere.Cai and Huang(2013)used the mechanical-Coriolis oscillation mechanism to show how the β-effect and topographic-effect induce Rossby waves.Song and Yang(2009,2010)and Song et al.(2009,2017)have studied solitary Rossby waves in barotropic fluids and stratified fluids using the Wentzel-Kramers-Brillouin theory.In the barotropic and baroclinic model,Schneider(2015)analyzed the mechanism for the westward propagation of Rossby waves on the β-plane.Yang(1987,1988)introduced the δ-surface approximation of the Earth’s surface by considering the second derivative of the Coriolis parameter with respect to latitude(the variation of β with the latitudinal δ-effect),revealing Rossby wave packet structural vacillation to exist in some basic currents or topographies on the Earth’s δsurface.

The object of this paper is,depending on potential vorticity conservation to describe Rossby wave propagation when modeling on the Earth’s δ-surface,a reference frame propagation with the zonal phase speed of the wave is used to analyze the physical mechanism of Rossby wave propagation.The results show that the variation in β with the latitudinal δ-effect has an important influence on the propagation of Rossby waves.

2.Barotropic Rossby waves on the Earth’s δ-surface

Following the shallow-water formulation of Holton(1979),Pedlosky(1979),and Gill(1982),the barotropic vorticity equation is

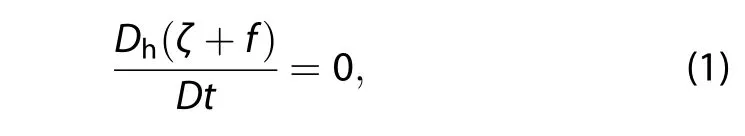
The Earth’s δ-surface approximation is the same as employed in Yang(1987,1988):

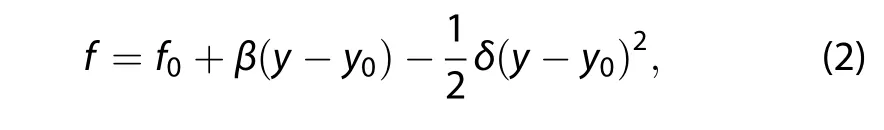
where the second derivative of the Coriolis parameter with respect to latitude has been included;f0is a constant midlatitude(at y0)Coriolis parameter;and β and δ are constants,defined as follows:

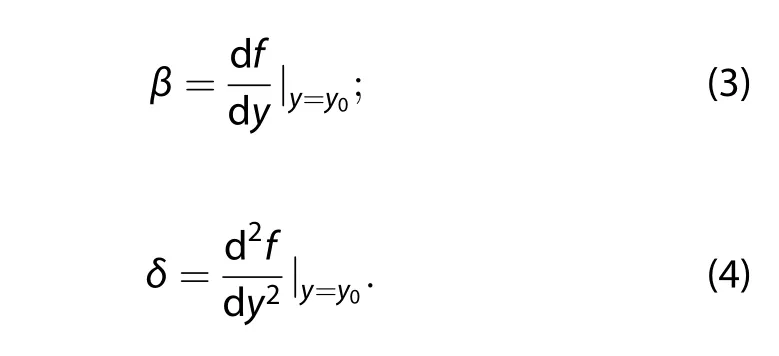
Here,f0,β,and δ can be taken as positive at the midlatitudes.Yang(1987,1988)showed the main difference between the Earth’s δ-surface approximation and the Earth’s β-plane approximation.The main difference is:on the β-plane the surface of the Earth is considered to be a plane whereas on the δ-surface;the surface of the Earth is considered to be a quadratic surface.

The δ-surface approximation is more realistic than the β-plane approximation,especially at higher latitudes(Liu and Tan 1992;Luo 1995).With d representing the change along a trajectory,Equation(1)can be reduced to

Then,Equation(2)gives

and it follows that

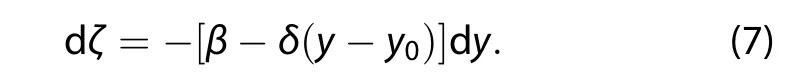
Using Equation(7),we draw the following main conclusions:

(1)For a northward displacement,dy＞0:if β - δ（y-y0）＞0,from Equation(7)the relative vorticity change is anticyclonic,dζ＜0;if β - δ（y-y0）＜0,the relative change vorticity change is cyclonic,dζ＞0.

(2)Fora southward displacement,dy＜0:if β - δ（y-y0）＞0,from Equation(7)the relative vorticity change is cyclonic,dζ＞0;if β - δ（y-y0）＜0,the relative change vorticity change is anticyclonic,dζ＜0.

(3)If the δ-effect is neglected,the conclusion of the relative vorticity coincides with the literature(Schneider 2015).

The material derivative of Equation(1)can be obtained as

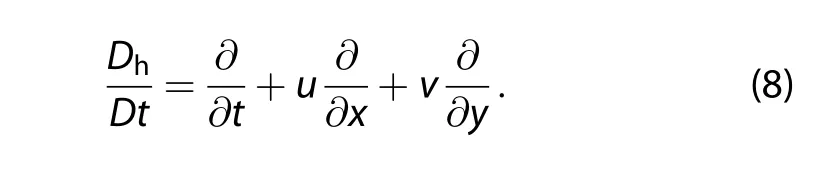
For a barotropic atmospheric model,the horizontal velocity(u,v)is nondivergent and given in terms of the streamfunction ψ,as

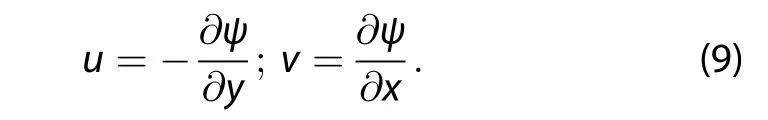
The relative vorticity is

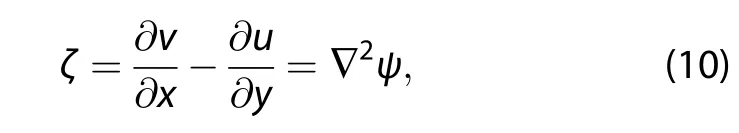
and the streamfunction is(Holton and Hakim 2012)

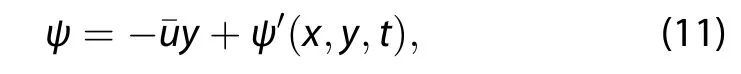
The solutions of Equation(12)are the same as employed in Holton and Hakim(2012):

where k and l are the local wave numbers in the zonal and meridional direction,respectively,and c is the phase speed of the barotropic Rossby waves.

Substituting Equation(13)into Equation(12),the dispersion relation can be obtained by

where K2=k2+l2is the full wavenumber.From

theRossbywavespropagatewestward,buttheδ-surface effect prevents the Rossby waves from propagating westward.Thus,the Rossby waves propagate westward relative to the basic state flow.Furthermore,the Rossby wave phase speed depends on the zonal,the horizontal,and the δ-effect.

(4)In the spherical coordinate system,the β-plane approximation is the same as employed in Liu and Liu(2011),Pedlosky(1979),and Grimshaw(1975):

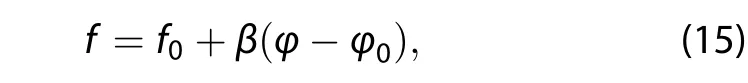
where f0=2Ωsinφ0and β =2Ωcosφ0are the Coriolis parameter and the Rossby parameter at the central latitude φ0,respectively,and Ω is the angular speed of rotationtotheEarth.Inthedispersionrelationofthespherical coordinate,the Rossby parameter β only plays the role of the spherical effect(Deng et al.2004;Li and Li 2012;Gu 2016).In the spherical coordinate and local Cartesian coordinate system,the classical β-plane approximation shows that the Coriolis parameter f is a linear function of latitude.It is convenient to use the Cartesian coordinate;on the δ-surface,the surface of the Earth is the Coriolis parameter as a quadratic function of latitude.Equation(14)shows that theEarth δ-surfaceapproximationismore realisticthantheδ-planeapproximation,andtheresulting equation,Equation(14),expresses the Earth’s curvature is not neglected in the Cartesian coordinate.

Transforming to the wave reference frame on the Earth’s δ-surface,the coordinates in the wave frame are the same as employed in Schneider(2015):

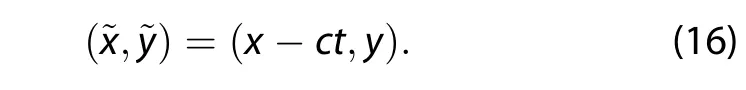
The streamfunction~ψ is

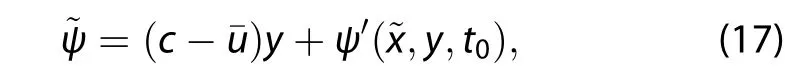
where t0is a constant,and the streamfunction~ψ differs from the streamfunction in the ground reference frame,Equation(11),such as in Schneider(2015).Equation(12)is given by in the wave frame

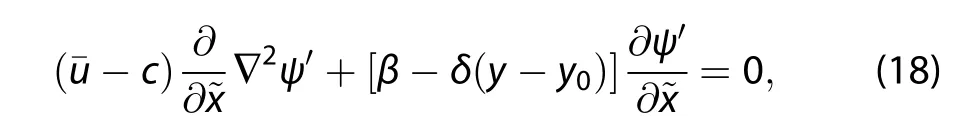
where

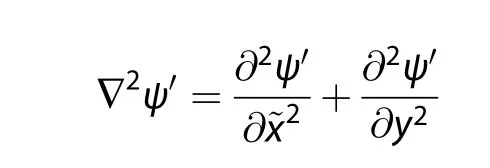
is the Laplace operator in the wave frame.The description of the conservation of absolute vorticity along trajectories parallels that of Schneider(2015)on the Earth’s δ-surface:

In the wave reference frame,d~ψ=0·along a trajectory and,following Equation(17),we obtain

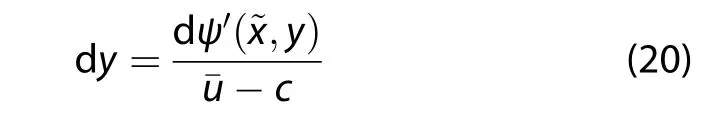
Here,ˉu-c≠0 and,using Equations(14)and(20)in the wave frame,the relative vorticity is

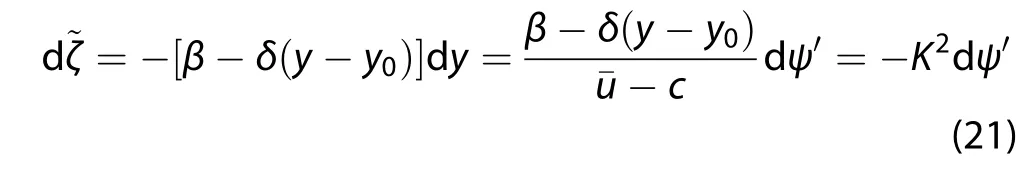
Equation(21)can be written as

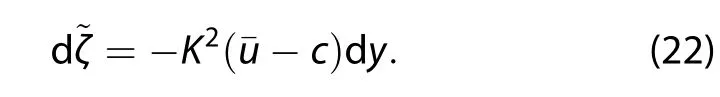
Equation(21)or Equation(22)shows the kinematic relationship:Under dy＞0(northward displacement)conditions,if β - δ（y-y0）is positive,and thus d~ζ is negative the parcels approach from the west,but the δeffect slows the parcels’westward movement,and this may be of great importance near the Earth’s poles.Where β =0,the relative vorticity d~ζ= δ（y-y0）dy,and thus d~ζ is positive.the parcels approach from the east.If β - δ（y-y0）is negative,in this case,from the kinematic relationship,Equation(22),the parcels approach from the east,and the δ-effect strengthens its eastward movement.Analysis of southward displacement(dy＜0)gives a similar result.

3.Baroclinic Rossby waves on the Earth’s δ-surface

The baroclinic quasigeostrophic potentialvorticity equation(Holton and Hakim 2012)is

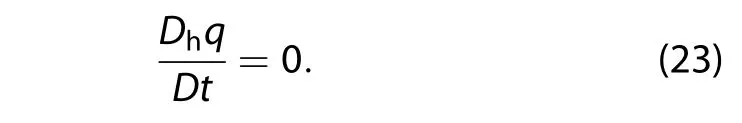
Here,

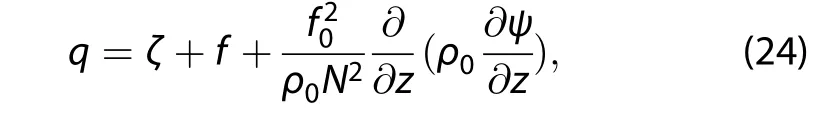
where the streamfunction ψ satisfies Equation(9);the definitions of z=-Hln（p/ps）,H=RTs/g,ps,Ts,R,ρ0,and N2parallel those in Holton and Hakim(2012);and theplanetary vorticity fsatisfies Equation(2).Assuming a small-amplitude disturbance on a constant zonal-meanflow,the streamfunction for a wave mode takes the form(Schneider 2015)

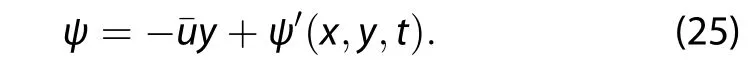
Substituting Equation(25)into Equation(23),the linearized version of Equation(23)is

The baroclinic Rossby wave solution to Equation(26)is the same as employed in Holton and Hakim(2012)and Schneider(2015):

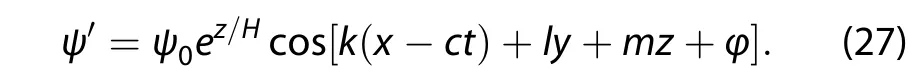
Here,the factor ez/H(which is proportional to ρ0-1/2)is included to simplify the equation for the vertical dependence,and m is the vertical wavenumber.With the substitution of Equation(27),the baroclinic Rossby wave dispersion relation on the Earth’s δ-surface can be obtained:

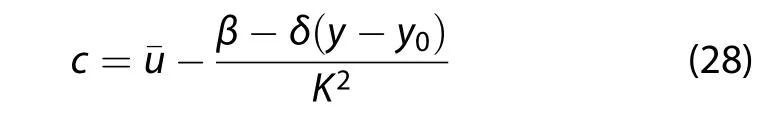
where the full wavenumber K2=k2+l2+ˉm2+λ-2,

From the dispersion relation,Equation(28),if

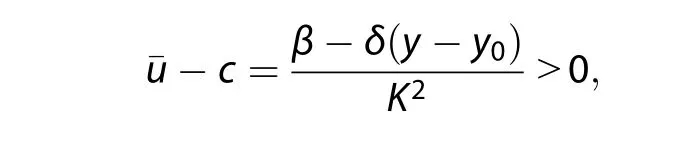
the baroclinic Rossby waves propagate westward with respect to the basic state flow,but the δ-effect suppress the Rossby waves propagating westward.Ifthe δ-effect promotes the eastward propagation of the baroclinic Rossby waves.

Analogous to the barotropic Rossby waves in the wave frame,

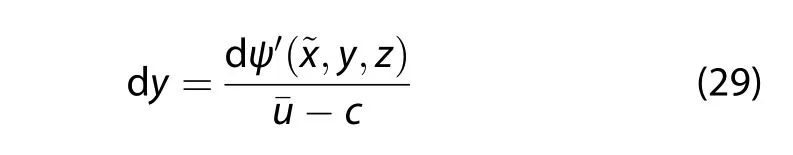
The relative vorticity is proportional to the streamfunction

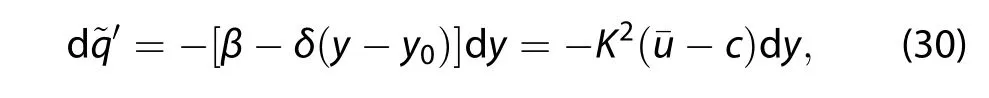
In the wave frame,from Equation(30),under dy＞0(northwarddisplacement):if(with β - δ（y-y0）＞0),parcels must approach from the west,but the δ-effect slows the parcels’westward movement;and ifˉu-c＜0(with β-δ（y-y0）＜0),parcels must approach from the east,and the δ-effect promotes the parcels’eastward movement.Analysis under southward displacement(dy＞0)gives a similar result.

4.Conclusions

From the above discussion,we can draw the following main conclusions:The conservation equation of potential vorticity based on the δ-effect of Yang(1987,1988)and Liu and Tan(1992)of Rossby waves cannot be ignored,especially in high-latitude regions,showing that the curvature of Earth is of great importance in the study of geophysical fluid dynamics.The propagation trajectory of barotropic and baroclinic Rossby waves is studied in a reference frame.Consequently,the δ-effect plays an important role in the propagation of barotropic and baroclinic Rossby waves.This effect increases the speed of the Rossby wave moving eastward,which weakens the westward propagation of the Rossby wave.

Disclosure statement

No potential conflict of interest was reported by the authors.

Funding

This study was supported by the National Natural Science Foundation of China[grant numbers 11362012,11562014,41465002,and 41765004]and the High School Science Research Project of the Inner Mongolia Autonomous Region[grant number NJZY16096],the Natural Science Foundation of Inner Mongolia[grant number 2018LH04005].