STRONG COMPARISON PRINCIPLES FOR SOME NONLINEAR DEGENERATE ELLIPTIC EQUATIONS?
Yanyan LI(李巖巖)
School of Mathematical Sciences,Beijing Normal University,Beijing 100875,China;
Department of Mathematics,Rutgers University,110 Frelinghuysen Rd,Piscataway,NJ 08854,USA
E-mail:yyli@math.rutgers.edu
Bo WANG(王博)
Corresponding author.School of Mathematics and Statistics,Beijing Institute of Technology,Beijing 100081,China
E-mail:wangbo89630@bit.edu.cn
Abstract In this paper,we obtain the strong comparison principle and Hopf Lemma for locally Lipschitz viscosity solutions to a class of nonlinear degenerate elliptic operators of the form ?2ψ+L(x,?ψ),including the conformal hessian operator.
Key words Hopf lemma;strong comparison principle;degenerate ellipticity;conformal invariance.
1 Introduction
In this paper,we establish the strong comparison principle and Hopf Lemma for locally Lipschitz viscosity solutions to a class of nonlinear degenerate elliptic operators.
For a positive integer n ≥ 2,let ? be an open connected bounded subset of Rn,the ndimensional euclidean space.For any C2function u in ?,we consider a symmetric matrix function

One such matrix operator is the conformal hessian operator(see e.g.[21,27]and the references therein),that is,

where I denotes the n×n identity matrix,and for p,q∈Rn,p?q denotes the n×n matrix with entries(p ? q)ij=piqj,i,j=1,···,n.Some comparison principles for this matrix operator have been studied in[22–25].Comparison principles for other classes of(degenerate)elliptic operators are available in the literature.See[1–5,7–20,26]and the references therein.
Let U be an open subset of Sn×n,satisfying

where P is the set of all non-negative matrices.Furthermore,in order to conclude that the strong comparison principle holds,we assume Condition Uν,as introduced in[25],for some unit vector ν in Rn:there exists μ = μ(ν)>0 such that

Here Cμ(ν):={t(ν ? ν +A):A ∈ Sn×n,kAk< μ,t>0}.Some counter examples for the strong maximum principle were given in[25]to show that the condition(1.3)cannot be simply dropped.
Remark 1.1If U satis fies(1.2),

where O(n)denotes the set of n×n orthogonal matrices,then it is easy to see that U satis fies(1.3).

in the viscosity sense,if for any x0∈ ?,? ∈ C2(?),(? ?u)(x0)=0((? ?v)(x0)=0)and
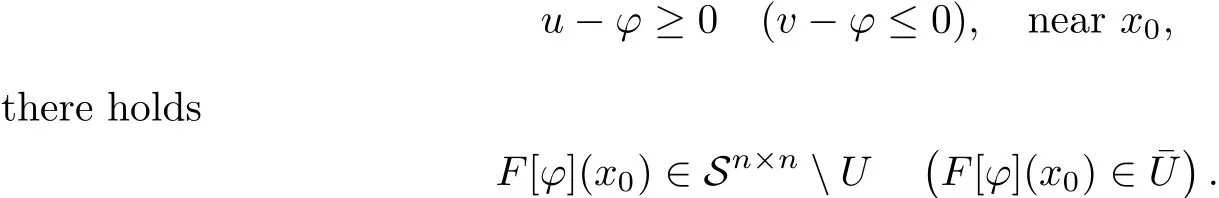
We have the following strong comparison principle and Hopf Lemma.
Theorem 1.2(strong comparison principle) Let ? be an open connected subset of Rn,n ≥ 2,U be an open subset of Sn×n,satisfying(1.2)and Condition Uνfor every unit vector ν in Rn,and F be of the form(1.1)with(1.4)in the viscosity sense,u ≥ v in ?.Then either u>v in ? or u ≡ v in ?.
Theorem 1.3(Hopf lemma) Let ? be an open connected subset of Rn,n ≥ 2,?? be C2near a pointand U be an open subset of Sn×n,satisfying(1.2)and Condition Uνforthe interior unit normal of?? at?x,and F be of the form(1.1)withAssume that u,vsatisfy(1.4)in the viscosity sense,u>v in ? andThen we have

Remark 1.4If u and v∈C2,then Theorems 1.2 and 1.3 were proved in[25].
2 Proof of Theorem 1.2
Proof of Theorem 1.2We argue by contradiction.Suppose the conclusion is false.Sinceis non-negative,the set{x ∈ ? :u=v}is closed.Then there exists an open ball B(x0,R)??? centered at x0∈? with radius R>0 such that

Indeed,the first part of(2.6)follows from the de finitions of u?and v?,and the fact that.Now we prove the second part of(2.6).By theorem 5.1(a)in[6],we have that
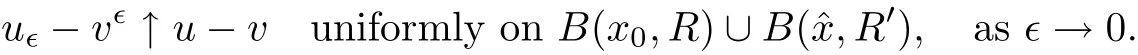
It follows that for any M>0,there exists ?0(M)>0 such that
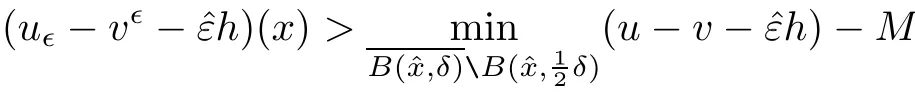
for any 0
It follows from(2.6)that there existssuch that for any η∈(0,ˉη),there existssuch that


And by lemma 3.5 in[6],we have
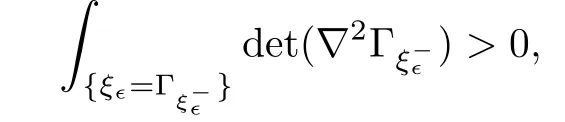
which implies that the Lebesgue measure ofis positive.Then there exists x?,η∈such that both of v?and u?are punctually second order di ff erentiable at
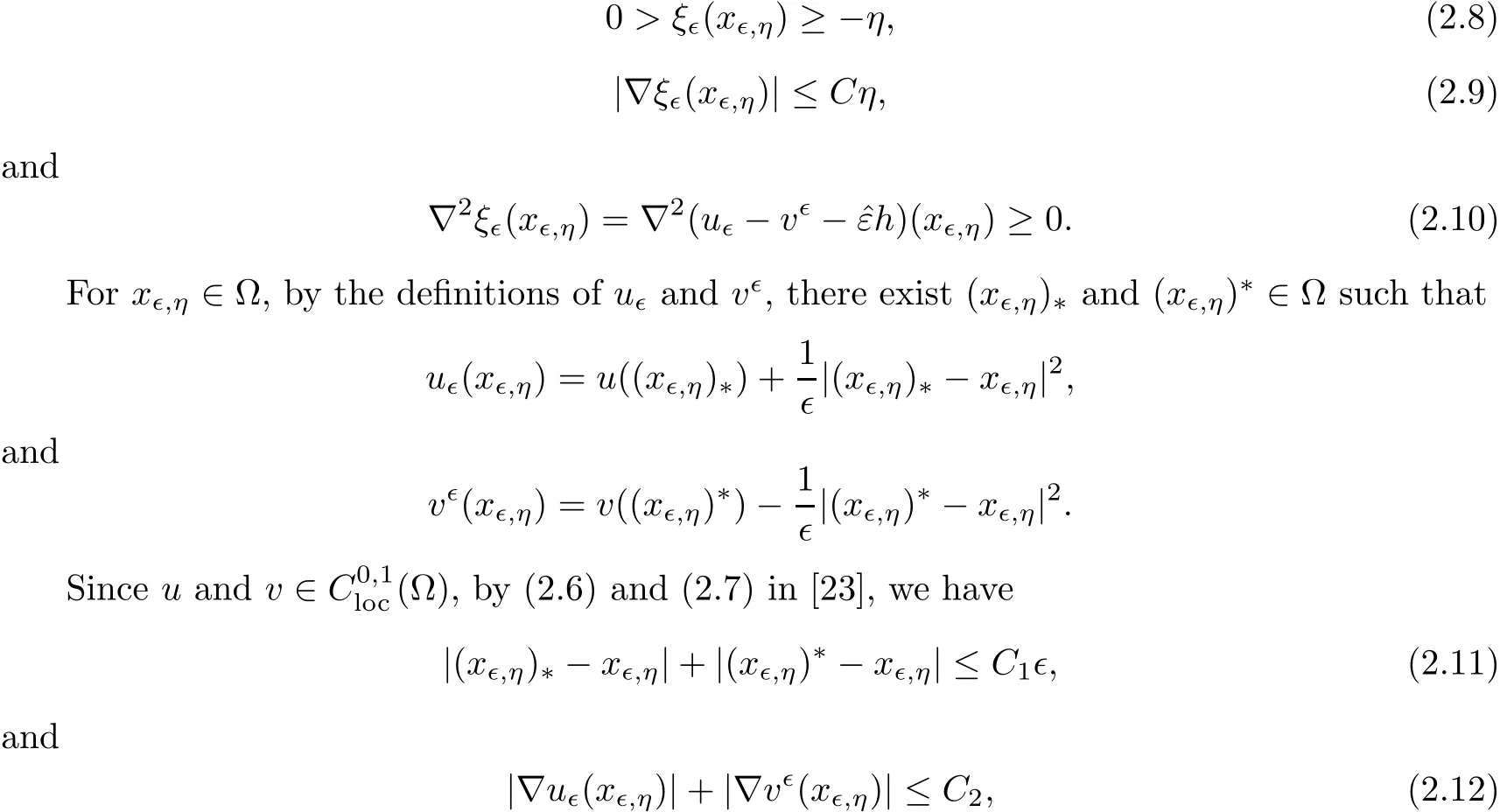
where C1and C2are two universal positive constant independent of ? and η.
Since u?is punctually second order di ff erentiable at x?,η,we have
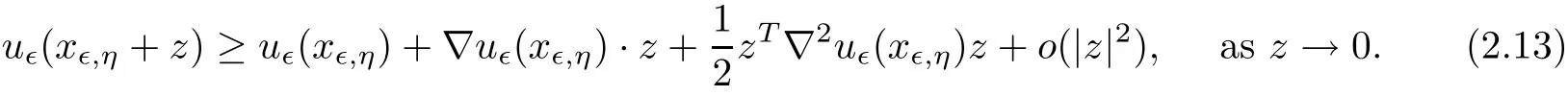
By the de finition of u?,we have
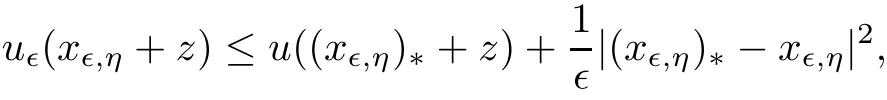
and therefore,in view of(2.13),


We can firstly fix the value of small δ>0 and a large α >1,then fix the value of small0,and lastly fix the value of small ? and η>0 such that
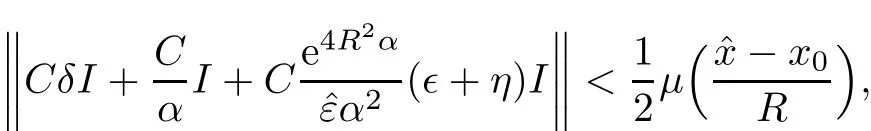
whereμis obtained from condition(1.3).
Therefore,by(1.3)and(2.21),we have that

which is a contradiction with(2.16).Theorem 1.2 is proved.
3 Proof of Theorem 1.3
Proof of Theorem 1.3Since?? is C2near,there exists an open ball B(x0,R)??such that

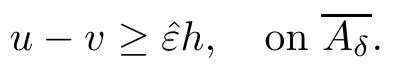
Once the claim is proved,then we have that
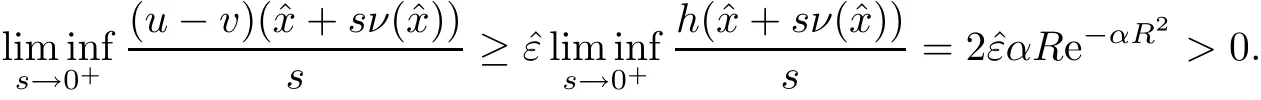
Therefore,in order to finish the proof of Theorem 1.3,we only need to prove the above claim.Suppose the contrary,that is,
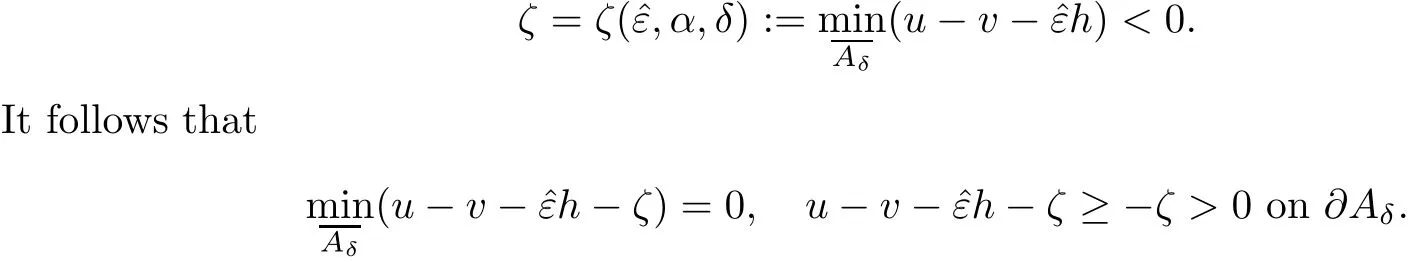
Now we can follow the argument as in the proof of Theorem 1.2 to get a contradiction.Theorem 1.3 is proved.
 Acta Mathematica Scientia(English Series)2018年5期
Acta Mathematica Scientia(English Series)2018年5期
- Acta Mathematica Scientia(English Series)的其它文章
- REVIEW ON MATHEMATICAL ANALYSIS OF SOME TWO-PHASE FLOW MODELS?
- H¨OLDER CONTINUOUS SOLUTIONS OF BOUSSINESQ EQUATIONS?
- RADIAL SYMMETRY FOR SYSTEMS OF FRACTIONAL LAPLACIAN?
- MACROSCOPIC REGULARITY FOR THE BOLTZMANN EQUATION?
- ONE-DIMENSIONAL VISCOUS RADIATIVE GAS WITH TEMPERATURE DEPENDENT VISCOSITY?
- STABILITY OF STEADY MULTI-WAVE CONFIGURATIONS FOR THE FULL EULER EQUATIONS OF COMPRESSIBLE FLUID FLOW?
