THE OSCILLATION OF THE POISSON SEMIGROUP ASSOCIATED TO PARABOLIC HERMITE OPERATOR?
Ping LI(李平)
School of Information and Mathematics,Yangze University,Jingzhou 434023,China
E-mail:liping@whu.edu.cn
Youliang HOU(候友良)
School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China E-mail:ylhou323@whu.edu.cn
AbstractLet O)be the oscillation of the Possion semigroup associated with the parabolic Hermite operator L=?t??+|x|2.We show that O(PτL)is bounded from Lp(Rn+1)into itself for 1 Key words oscillation operator;Possion semigroup;parabolic Hermite operator Given a family of operators T={Tt}t>0between spaces of some kind of functions,the oscillation operator associated with T is defined by where{tj}is a sequence of real numbers tending to 0 as j→?∞ and∞ as j→∞.Many recent research papers were devoted to oscillation inequalities(or variation inequalities)in harmonic analysis and probability theory,see for instance[1–3,5,6,8,11].One important feature of these inequalities is the fact that they immediately imply the pointwise convergence of the underlying family of operators without using the Banach principle via the corresponding maximal inequality.Moreover,these inequalities can be used to measure the speed of convergence of the family. The purpose of this paper is to study oscillation inequalities for the Poisson semigroup of the parabolic operator L= ?t? ?+|x|2,which in PDE,is directly associated with the space-time nonlocal heat equation To obtain the solutions of this equation,the authors considered the negative powers L?1by using a absolutely convergent complex valued integral(see[10]). Let hk(r)(r∈R)be the collection of Hermite functions on the real line where Hk(r)denotes the classical Hermite polynomial of degree k.The multidimensional Hermite functions are hα(x)=hα1(x1)···hαn(xn)for α =(α1,···,αn) ∈x ∈ Rn.Let H=??+|x|2be the harmonic oscillator operator,which is a positive and symmetric operator in L2(Rn)with domain Cc∞(Rn).It is well known that the Hermite functions give the spectral decomposition of H in L2(Rn)with Hhα=(2|α|+n)hα,where|α|= α1+···+ αn.The heat semigroup{e?τH}τ>0is given by integration against a kernel,see[16].Indeed,for smooth function ? with rapid decay at infinity, It is easy to check that where the complex integral is absolutely convergent,see for example[15].By using formula above the authors in[10]defined where e?τ(?t+H)is given by the composition Observe that the operators?tand H commute,then Hence,the parabolic heat semigroup associated with the parabolic Hermite operator L=?t? ?+|x|2= ?t+H has a kernel,that is for smooth function ?(x,t)with rapid decay at infinity,where Parallel to the classical case(cf.[14]),by using Bochner’s subordination formula,the parabolic Poisson semigroupassociated with Hermite operator is given by Our intention in this paper is to obtain the oscillation estimates for the family T={Tτ}τ>0when the family is the parabolic Poisson semigroup.Notice that the subordinated formula(1.3)implies that the Poisson semigroup is represented by a type of integral mean of the heat semigroup.Then the boundedness of the oscillation of the Poisson semigroup could be previously obtained by the corresponding one of the heat semigroup.Consequently,the authors in[2]proved the Lp(1 In this paper,we consider the boundedness for a kind of special oscillation O(defined as following.Let{aj}j∈Zbe an increasing sequence of positive numbers such that 1 ≤ aj+1/aj Typical examples of the sequence{aj}j∈Zare provided by exponential sequences such as aj=qj(j∈Z)for some constant q≥1. Now,we present the main results of this paper. Theorem 1.1 Let T={Pτ}τ>0be the Poisson semigroup associated with the parabolic Hermite operator L=?t??+|x|2.Then the oscillation operator Odefined in(1.4)is bounded on Lp(Rn+1)for 1 The behavior of the operator O(T)in L∞constitutes of the other interesting result of this paper.Wang[17] first found that there exists a function f∈L∞(Rn)such that the classical g-function g(f)=∞ almost everywhere although the g-function is bounded from(Rn)to BMO(Rn).The author also proved that if f∈BMO(Rn)and g(f)<∞a.e.,then kg(f)kBMO≤CkfkBMO.Betancora,Crescimbenia and Torrea[1]discussed systematically the behavior of the ρ-variation of the heat semigroup associated the harmonic oscillator H= ??+|x|2in L∞. We now present our L∞r(nóng)esults of the oscillation associated with the parabolic Poisson semigroup for Hermite operator.By the vector-valued Calderón-Zygmund theorem,we prove that Ois bounded from(Rn+1)to BMO(Rn+1),as stated in Theorem 1.1.In the case p=∞we characterize the local growth of the operator O(in L∞,see Theorem 1.2. Remark 1.3 The result of Theorem 1.2 shows that in some sense the oscillation operator O()is smaller than a standard singular integral operator. Throughout this paper,by C we always denote a positive constant that can change form line to line.We will make frequent use,sometimes without explicitly mentioning it,of the fact that,for every positive constant C and non-negative constant c, The organization of the paper is as follows.In Section 2,we deduce the L2boundedness of the oscillation operator O(PτL)by using Fourier transform and Plancherel’s identity.In Section 3,we prove that the vector-valued kernel of the operator O()satisfies the size condition and smoothness condition which allows us to get the proof of Theorem 1.1 by vector-valued Calderón-Zygmund theory.Finally,In Section 4 we devote to the proof of Theorem 1.2. We recall first the Calderón-Zygmund theory in spaces of homogeneous type that we will use in the particular case of the parabolic metric space. Let X be a set.A function ρ :X × X → [0,∞)is called a quasidistance in X if for any x,y,z ∈ X we have(1)ρ(x,y)= ρ(y,x),(2)ρ(x,y)=0 if and only if x=y,and(3)ρ(x,z) ≤ k(ρ(x,y)+ ρ(y,z))for some constant k ≥ 1.We assume that X has the topology induced by the open balls B(x,r)with center at x∈X and radius r>0 defined as B(x,r):={y ∈ X:ρ(x,y) Given a Banach space E,we denote by(X)=Lp(X,E)(1≤p<∞)the space of E-valued functions of defined on X such that kfkEbelongs to Lp(X,μ). Definition 2.1(vector-valued Calderón-Zygmund operator on(X,ρ,μ)) Let E,F be Banach spaces.We say that a linear operator T on a space of homogeneous type(X,ρ,μ)is a Calderón-Zygmund operator if it is satisfies the following conditions: (I)There exists 1≤p0≤∞such that T is bounded fromX)into(X). (II)For bounded E-valued function f with compact support,Tf can be represented as where K(x,y)∈L(E,F),the space of bounded linear operator from E to F,satisfies that for some constant C>0, whenever ρ(x,y0)>2ρ(y,y0). The Calderón-Zygmund theorem says that if T is a Calderón-Zygmund operator on(X,ρ,μ)as above then T is bounded from(X)into(X)for any 1 and dxdt is the Lebesgue measure on Rn+1.Observe that in this case,B((x,t),r)={(y,s)∈Rn+1:|x?y|+|t?s|1/2 so dxdt is doubling on parabolic balls as required. In order to prove the boundedness of the operatorby using the Calderón-Zygmund theorem,we need to show thatis a Calderón-Zygmund operator.We prove first thatis L2bounded.We first give a lemma as following,see[9]. Since the square root of complex number z=reiθhas two opposite valuesambiguity,here and in the following we takeconvention. Lemma 2.1 Let ξ∈ Rnand ρ ∈ R.Then there exists a constant such that Proof Let z0=(iρ +|ξ|2)and θ=argz0.We havehenceMoreover,we have This proves the lemma. If a function f(x,t)is defined on E=R×(0,∞),we shall imagine it to be extended to a function defined on Rn+1,identically zero for t≤0.Then we define the Fourier transform Lemma 2.2 Consider the collection of function The proof is completed. Proof Since A in Lemma 2.2 is dense in L2,it suffices to prove that the conclusion holdsBy using the Plancherel’s identity,Fubini’s theorem and Lemma 2.2,we have the last inequality follows from H?lder’s inequality.Notice that(C+1)ajsincethe computation above,we have the last inequality comes from Lemma 2.1.Therefore,by using Plancherel’s identity again and(2.2),we get The proof is completed. In Section 2,we have proved that the operatoris bounded on L2.In order to prove that the operatoris of(p,p)type(1 Observe that thus Therefore the Lpboundedness of the operatoris equivalent to the Lpboundedness of the operator T.It is know that if the operator T can be expressed as a singular integral operator and the kernel satisfies the so called size condition and smoothness condition,then T is a Calderón-Zygmund operator.Thus,the L2boundedness of T implies T is of(p,p)type(1 Theorem 2.1 and(3.2)give that the operatorT is bounded from L2(Rn+1)into(Rn+1).Now we prove that the operator T can be expressed as a singular integral and the kernel satisfies the required conditions.By using Fubini’s theorem,from(1.3)we get that Although gj(x,y,s)is defined only onwe can extend it to the whole space Rn+1by defining gj(x,y,s)=0 for s<0.The kernel is obviously smooth with respect to the variables s and y.Hence,we get the singular integral with variable kernel We introduce the following notations In particular,from(3.3),we can write In order to get size and smoothness conditions of the kernel gj(x,y,s)it is enough to get them for s>0.On this way we need some easy estimates that we present here for future reference. Remark 3.1 Let s>0. (ii)If s>1,then sinh2s~es,coth2s~es,coth2s~C,tanh2s~C,sinhs~es,coshs~es,coths~C,tanhs~C. Theorem 3.1 Let gj(x,y,s)be the function defined in(3.3).Then Before beginning proof of Theorem 3.1,we present a lemma that will be used in this section,see[9]. Lemma 3.1 For any integer N≥1 and constant C>0,define Proof of Theorem 3.1 (i)From(3.4)we get moreover,from(3.5),we get Case 1 If s<1.By using(3.6)and Remark 3.1 and Lemma 3.1,we obtain that Case 2 If s>1.From(3.6)and Remark 3.1,we get that The second inequality in(3.7)comes as follows.thenThus The proof of Theorem 3.1(i)is completed. (ii)It suffices to show Indeed,from(3.4)we have It is to check that By a parallel argument to the one in the proof of(3.6),we obtain that We start to estimate the first term I.If s<1.Then,from Remark 3.1 and Lemma 3.1 we have On the other hand,when s>1.By using the same argument in the proof of(3.7),we get that I is controlled byAnalogously,It is easy check that II is controlled byThus,we get (iii)The rest of the proof is exactly similar as the corresponding part above.But in this part,the computation is more complicated.We leave to the reader to complete the rest of the proof. ? Proof of Theorem 1.1 It is easy to get that the operator T in(3.1)satisfies conditions(II.1)and(II.2)in Definition 2.1 by using Theorem 3.1.Hence,the operator T is a Calderón-Zygmund operator by using Theorem 2.3.Then we immediately get that Theorem 1.1 holds by identity(3.2). ? In this section,we shall discuss the growth of the oscillation operatorIt turns out that O()is smaller than general Calderón-Zygmund operators in some sense,according to Theorem 1.2,we now give the proof of Theorem 1.2. Proof of Theorem 1.2 Recall that in Section 3,we proved that We can extended gj(x,y,s)to the whole space Rn+1just by setting gj(x,y,s)=0 for s≤0.It is clear that gjand its all derivatives are continuous.By using the H?lder’s inequality,we have From Remark 3.1,we have If s<1.Then where C is a constant which is independent of j.If s>1,analogously,we have By using Fubini’s theorem,we have By the same argument with the proof of Theorem 3.1,we obtain that Combining(4.1)and(4.2),we have Given Br=B(x0,r)? B0=B(0,1),we write f=f1+f2,where f1=fχB(x0,4r).Since O)f is bounded on Lp(Rn+1)for 1 On the other hand,it follows that from(4.4), Combining(4.4)and(4.5),we obtain that This proof is completed. AcknowledgementsThe first author would like to thank Prof.José Luis Torrea for inspiring this paper.1 Introduction
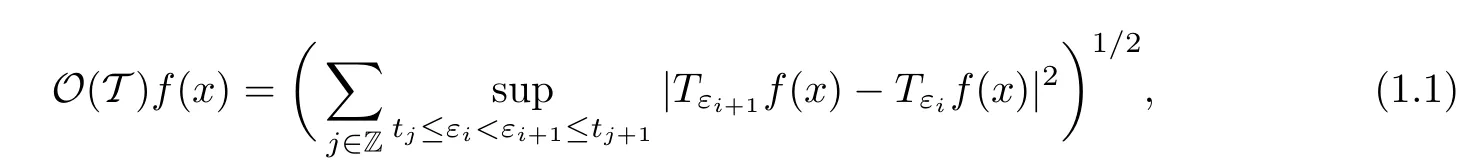
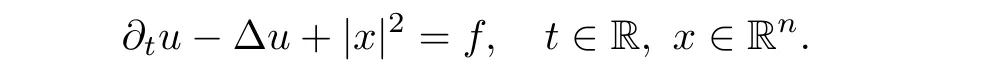



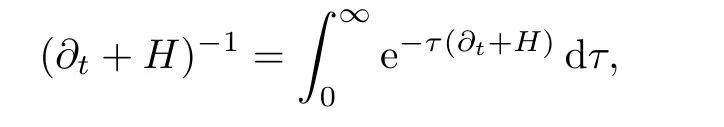


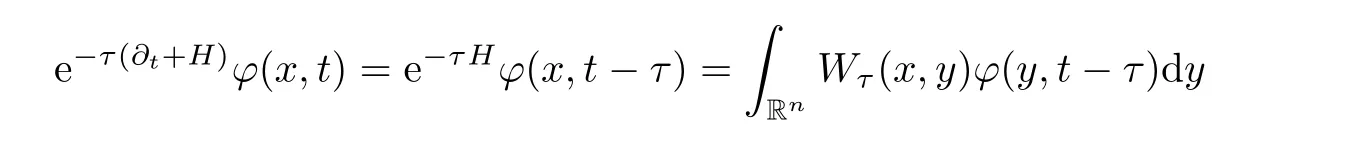
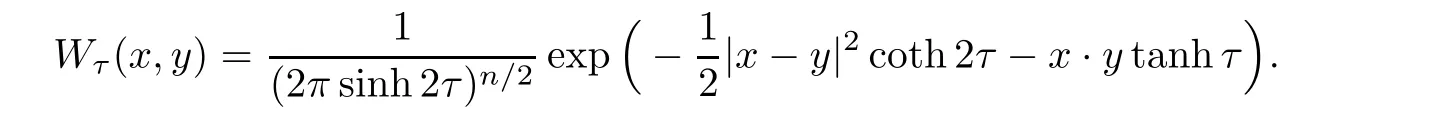
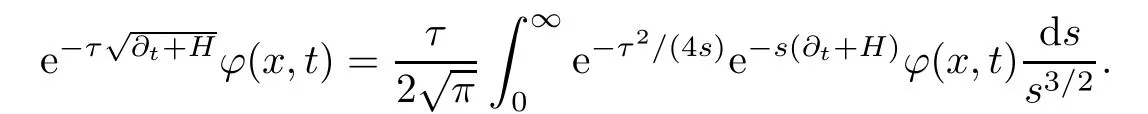


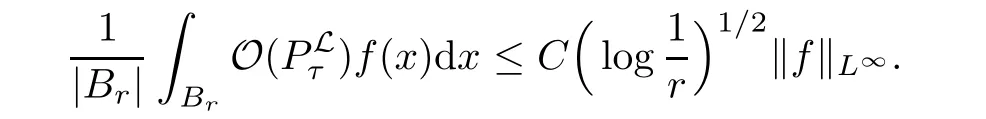
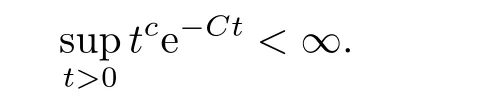
2 L2Estimate
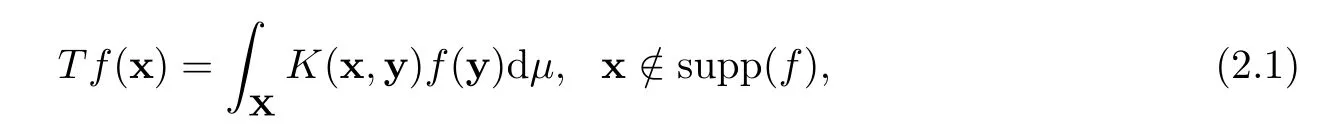

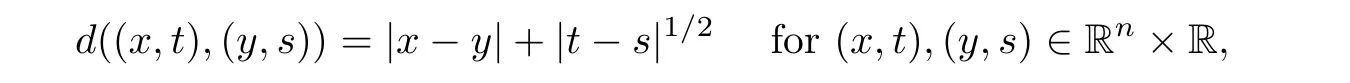
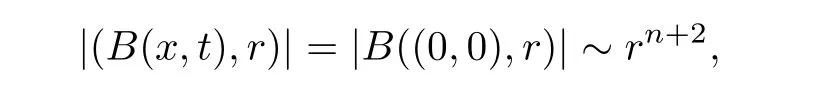
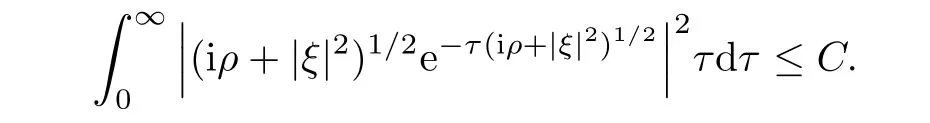
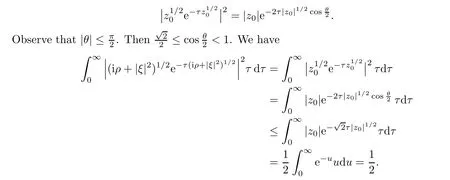
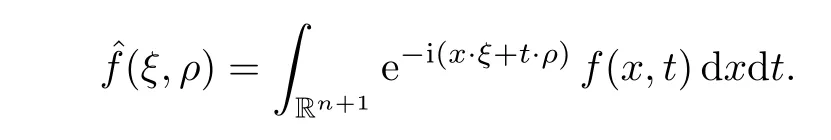

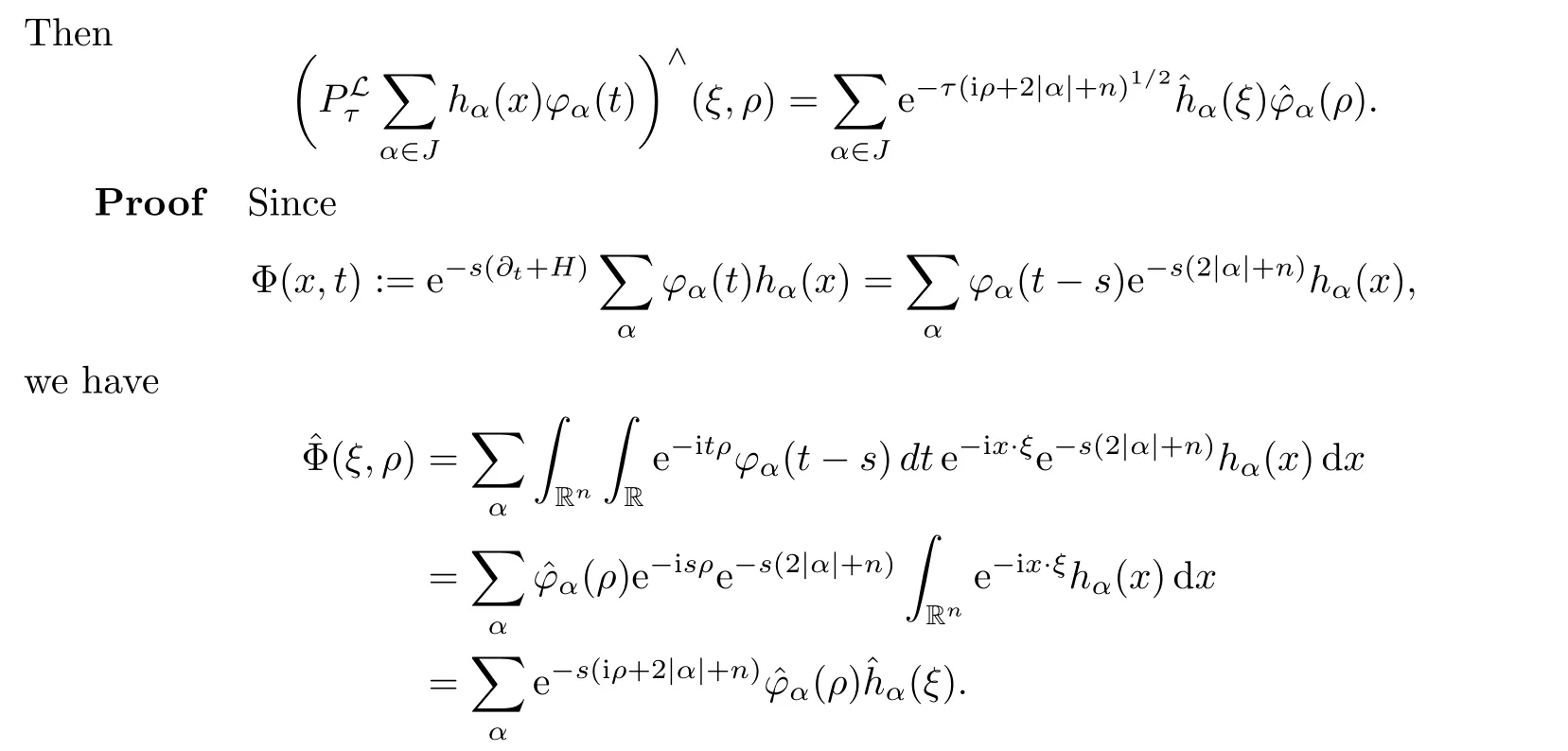
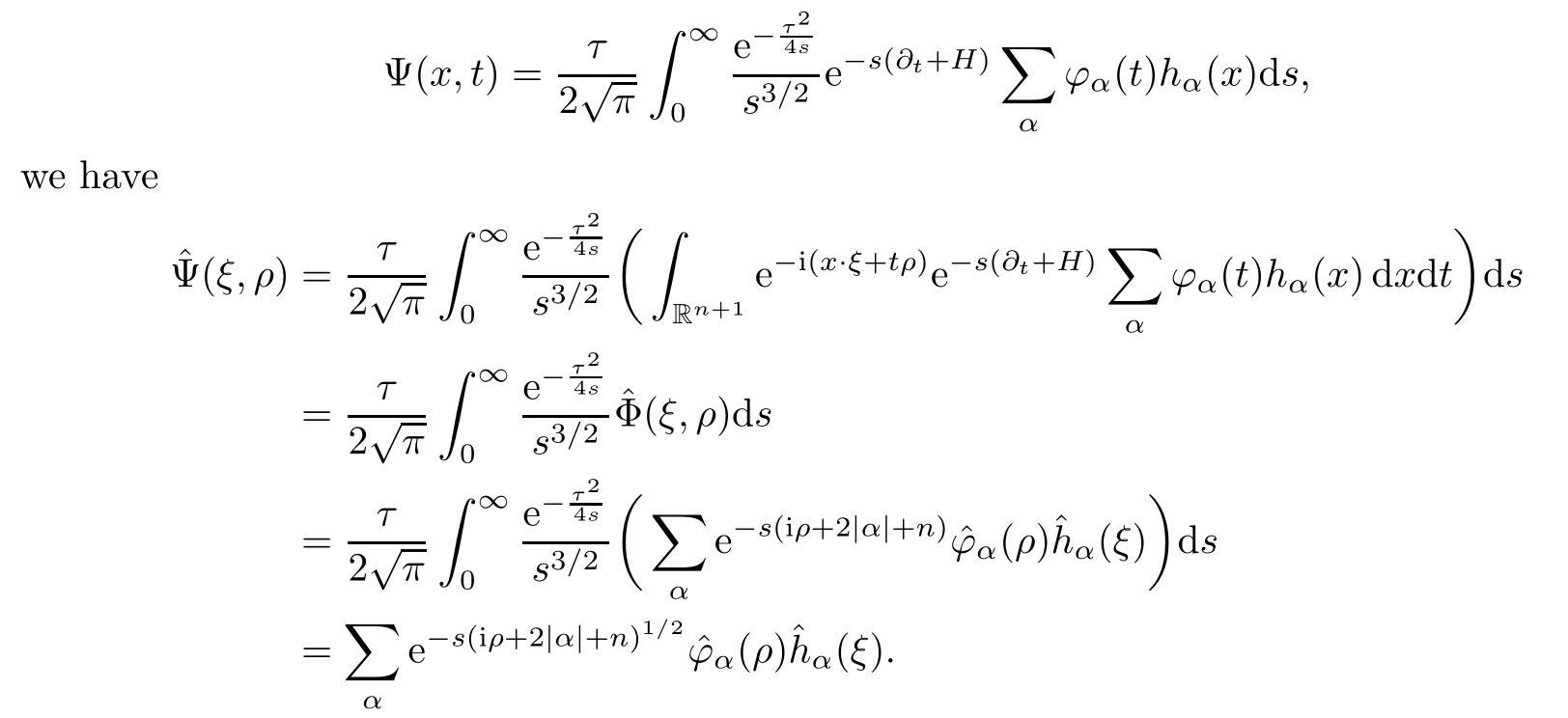



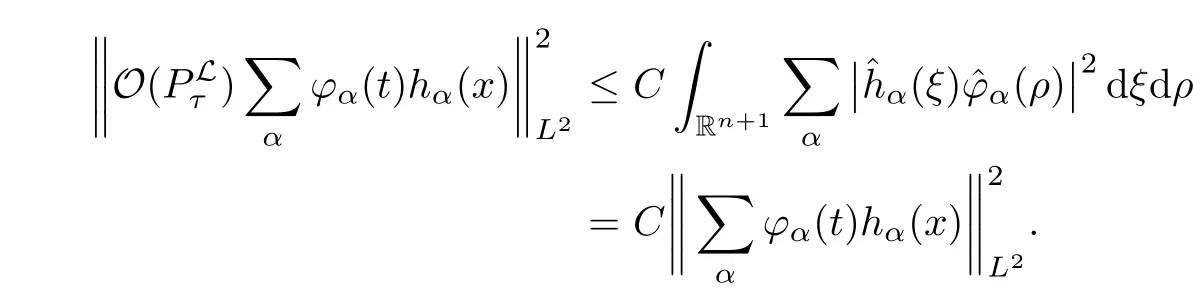
3 The Standard Estimates for the Kernel

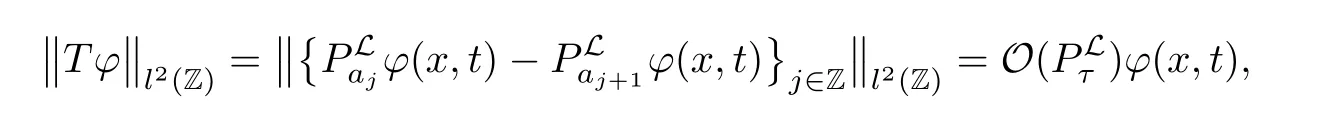
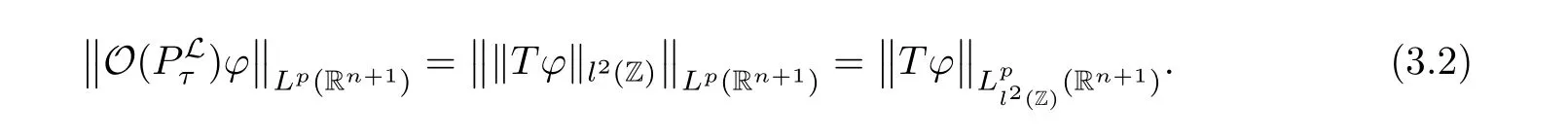
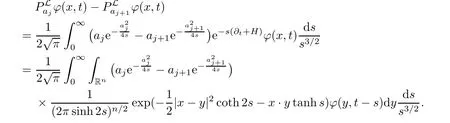
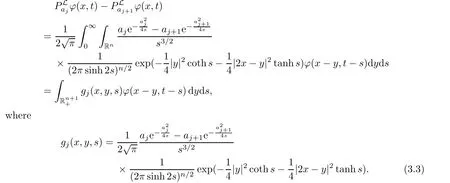



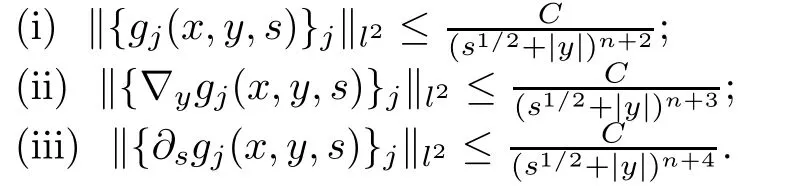

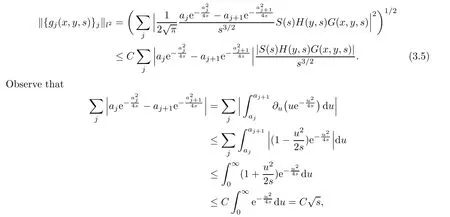
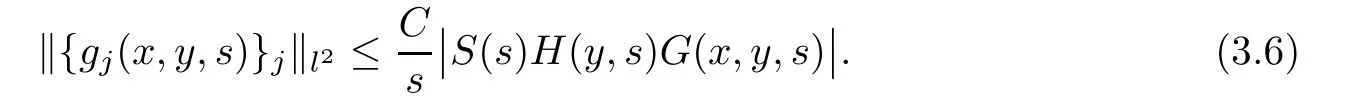
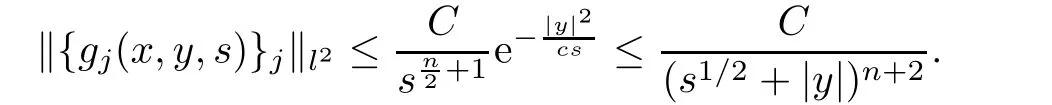
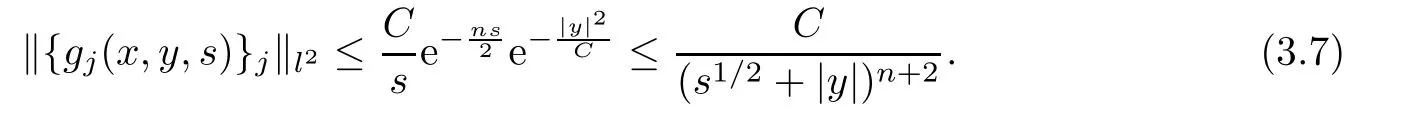

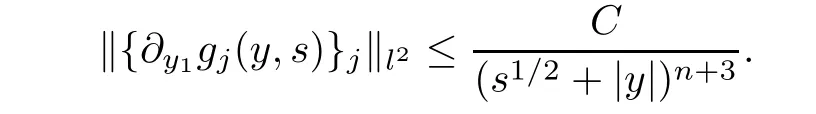
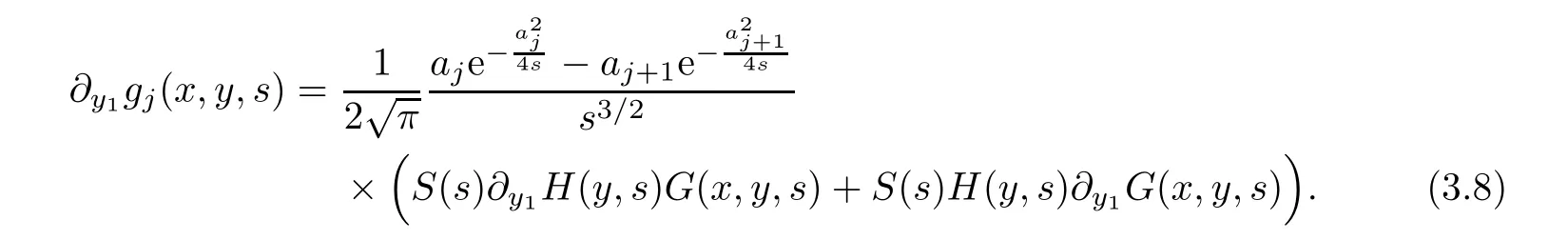
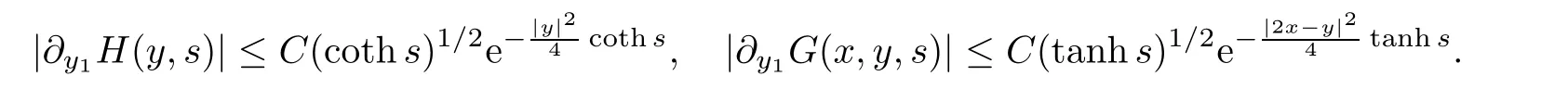
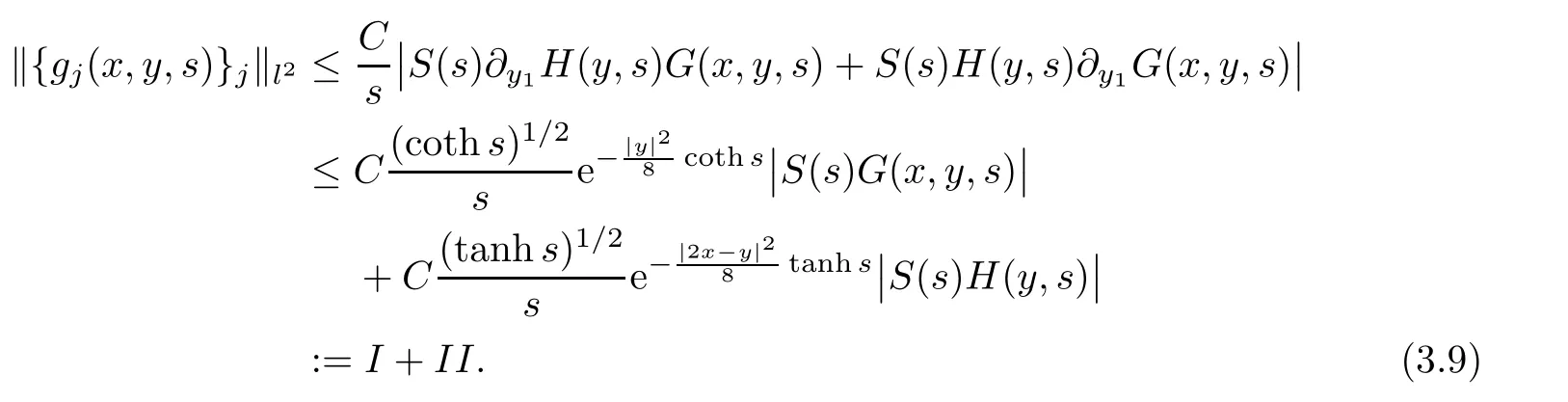


4 Growth of the Oscillation Operator O(PL τ)
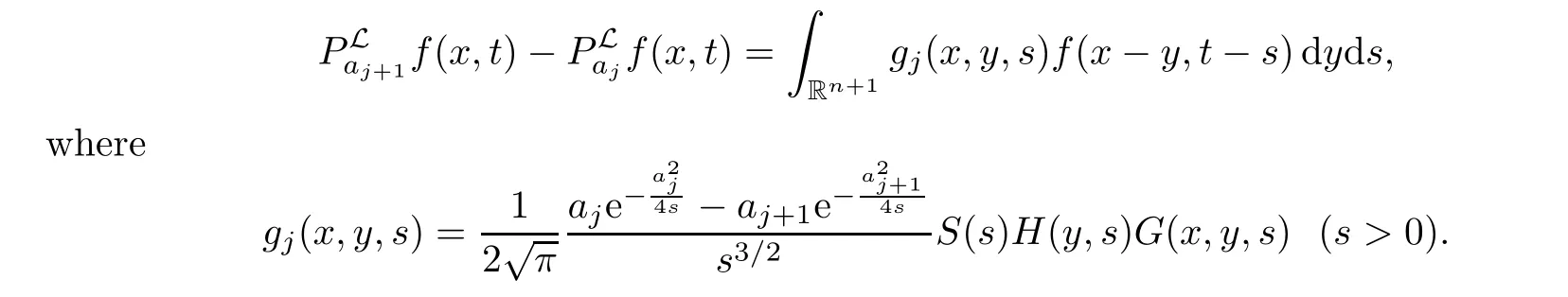
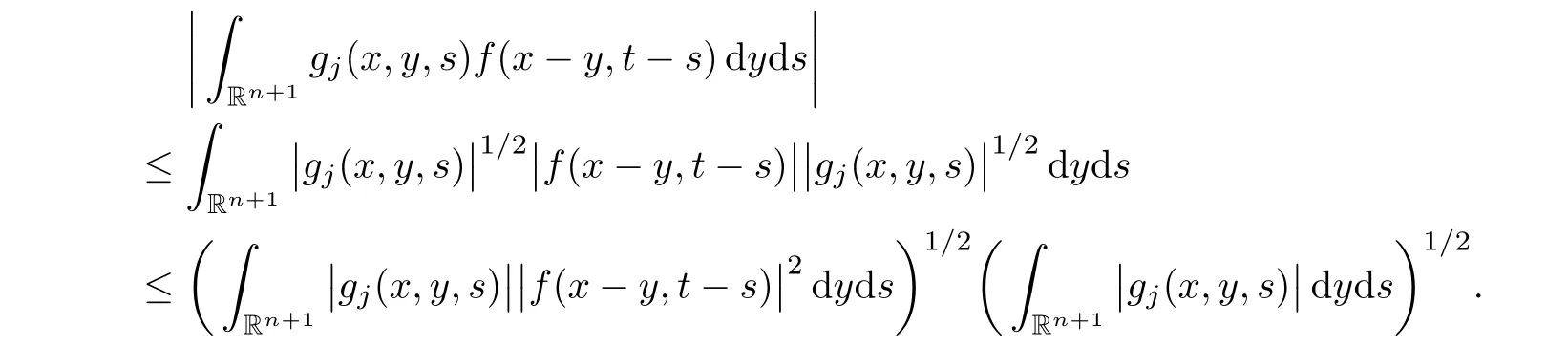
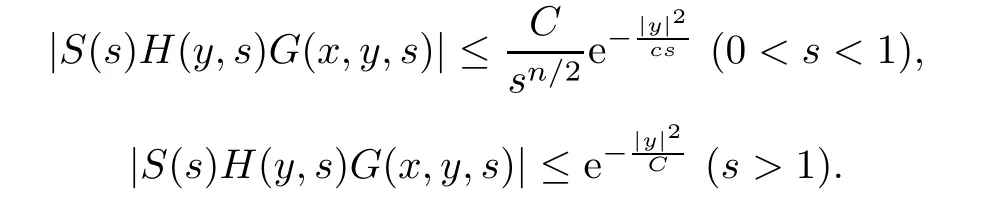
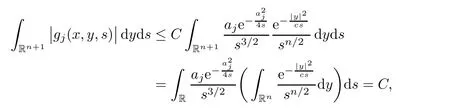
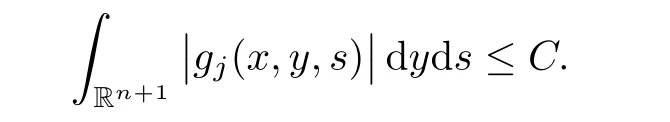
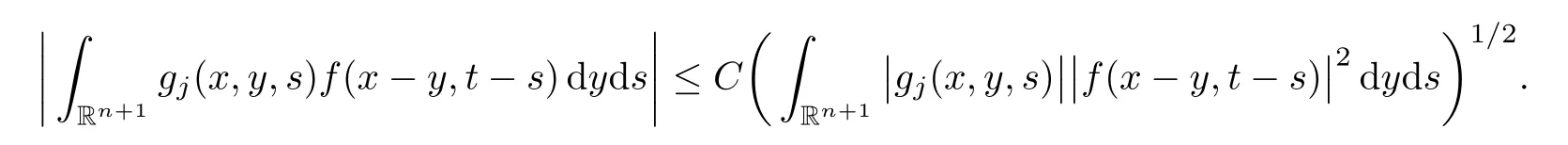
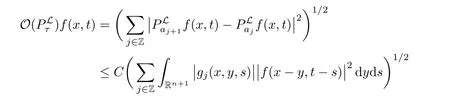
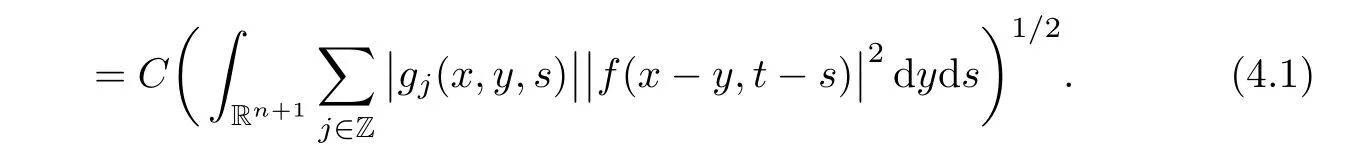
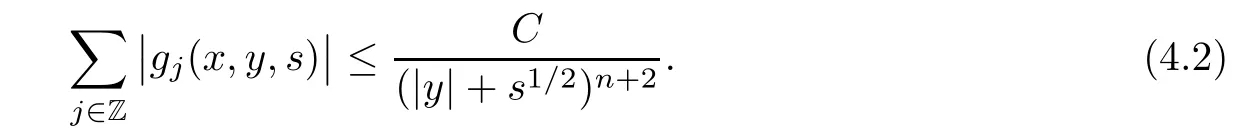
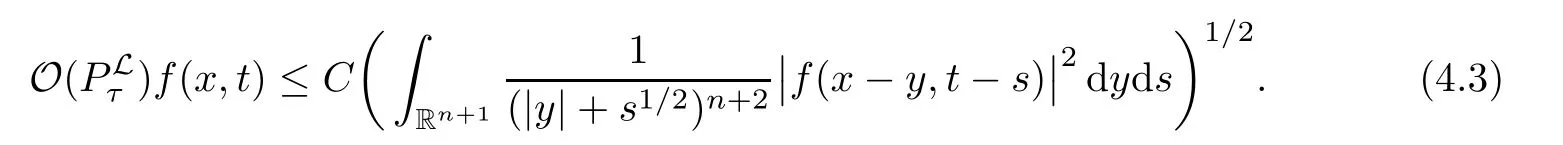
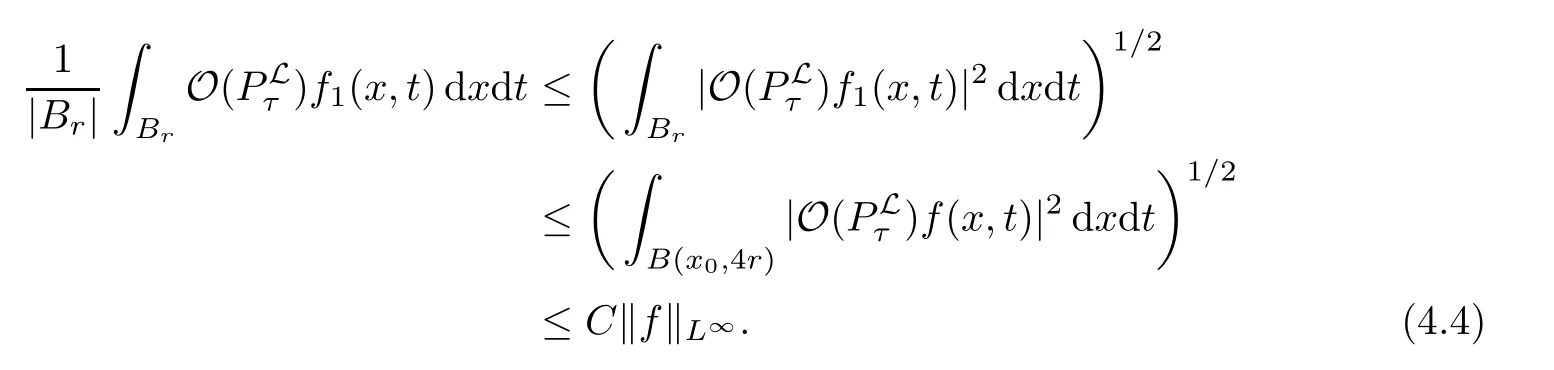
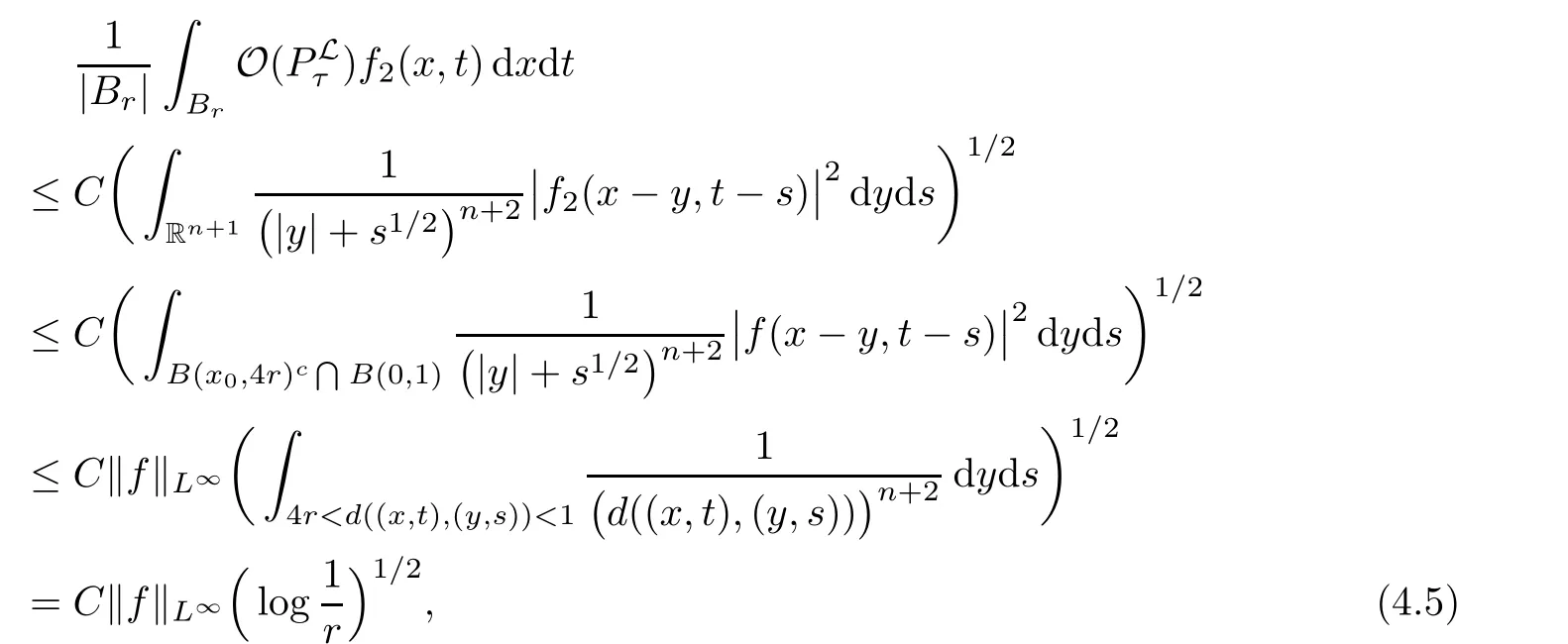
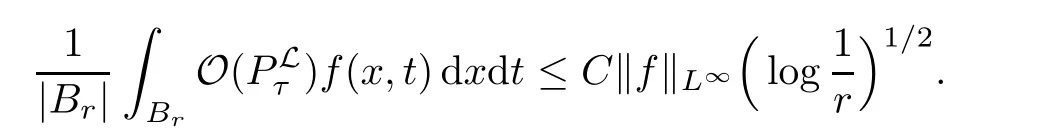
 Acta Mathematica Scientia(English Series)2018年4期
Acta Mathematica Scientia(English Series)2018年4期
