Ying Wang(王穎) and Shu-Yu Zhou(周蜀渝)

1School of Science,Jiangsu University of Science and Technology,Zhenjiang 212003,China

2Key Laboratory for Quantum Optics,Shanghai Institute of Optics and Fine Mechanics,Chinese Academy of Sciences,Shanghai 201800,China

AbstractWe investigate solitary vortex evolution in two-dimensional Bose-Einstein condensates based on the Gross-Pitaevskii equation model.Through the variational method,together with the novel Gaussian ansatz incorporating asymmetric perturbation effects,we arrive at the analytical solitary vortex solution with two typical forms:a symmetric quasi-stable solution under certain parametric settings and a diverging propagation case arising from an initial asymmetric perturbation.The derived pictorial evolutionary patterns of the solitary vortices are compared with those from a pure numerical analysis,and by identifying the key qualitative features,we show the applicability of the theoretical treatment presented here.

Key words:solitary vortex,Gross-Pitaevskii equation,Bose-Einstein condensate

1 Introduction

Nonlinear phenomena that occur in ultracold atomic systems,such as optical media involve many intriguing problems for experimental,as well as theoretical studies.Solitons and vortex are among the most appealing nonlinear features that have been extensively studied during the past two decades.One particular concern for the occurrence of the soliton/vortex is the stability issue that has been predicted in competing nonlinear media.[1]Nowadays,the inter-particle’s nonlinear interaction strength can be tuned continuously from ?∞ to+∞ (with“+”and “?”representing the repulsive and attractive interactions,respectively)via the Feshbach resonance experimental technique.[2?3]It has been proven both experimentally and theoretically that stable solitons can exist in a one-dimensional system.It has also been shown that the nonlocality influence of the nonlinearity[4]can prevent the collapse,and modulational instability[5]can be avoided if the nonlinearity is confined within a certain threshold value.White-solitons are a nonlinear phenomenon that can perform periodic motions and have been shown to be stable.[6]In a two-dimensional system,vortex phenomena commonly occur.It was shown that in self-focus media,the propagating vortices are relatively stable because of the modulated nonlinearity,[7]and the instability of the vortexes can be suppressed significantly resulting in the possible formation of quasi-stable rotating or breathing states.[8]

In this study,we theoretically derive the evolutionary pattern for the vortex in the two-dimensional Bose-Einstein condensates(BEC)system.Based on the twodimensional Gross-Pitaevskii equation(GPE)[9?17]and the variational methodology,[18?19]we derive the analytical solitary vortex solution describing the evolutionary behavior of the vortex.We identify that under different initial conditions,the vortex can either evolve into the quasi-stable pattern under appropriate parametric settings or diverge and propagate away into a twin pair pattern from an initial slight asymmetric perturbation.The key features of the two evolution scenarios are found to match those of prior numerical studies.[20?21]Moreover,our analysis can be extended to the vortices with higher vorticity,demonstrating the applicability of the theoretical treatment presented here.

This paper is organized as follows:Section 2 provides a description of the two-dimensional GPE model and procedural details of the variational approach used in the derivation of the analytical vortex solution.Two categories of results are discussed and pictorially demonstrated here.Section 3 presents a brief discussion of the possible extension of the current theoretical methodologies regarding vortices with higher vorticity.We present the conclusive remarks in Sec.4.

2 Two-Dimensional GPE Model and the Solitary Vortex Solution

We consider the two-dimensional situation where the Bose-Einstein condensate is tightly confined in the axial direction,and loosely confined in the transverse direction with harmonic potentialThe 2D Gross-Pitaevskii equation that governs the meanfield dynamics of the Bose-Einstein condensate is,

Eq.(1)is derived from the variation of the following action,

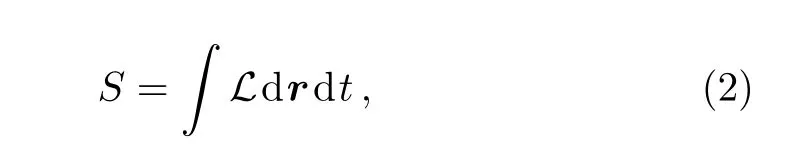
where the Lagrangian density takes the following form,

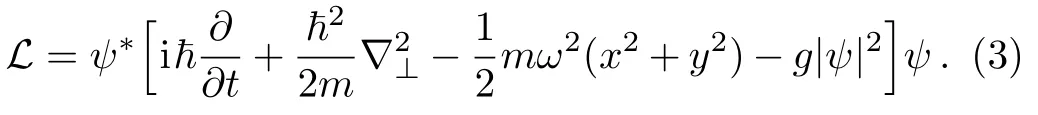
To obtain the analytical expression for ψ(x,y,t),we assume the following variational ansatz,

which corresponds to the solitary vortex with vorticity S=1[In exp(iS?)].We rede fined σx(t),σy(t),and k(t)as follows

where we assume that the system starts to evolve at time t=0 from the cylindrically symmetric stateThe dynamic evolution features of the system are determined by the evolutionary behavior of the parametric functions σ(t), θ(t)and φ(t).The three parametric functions are not independent.In fact,we determine two constraint formulae and assume that θ(t),and φ(t)are functions of σ(t).The two constraint formulae are obtained by substituting the ansatz of Eq.(4)into Eq.(1)and consider the imaginary part[18](proportional to iψ or i(x+iy)E,E is de fined as follows)of Eq.(1),which corresponds to the system’s continuity equation

Also the asymmetric terms(proportional to(x?iy)E)should not be present,which together with the imaginary part of Eq.(1)consist a polynomial of x and y.This requires that all the coefficients of these terms are set to zero as

where

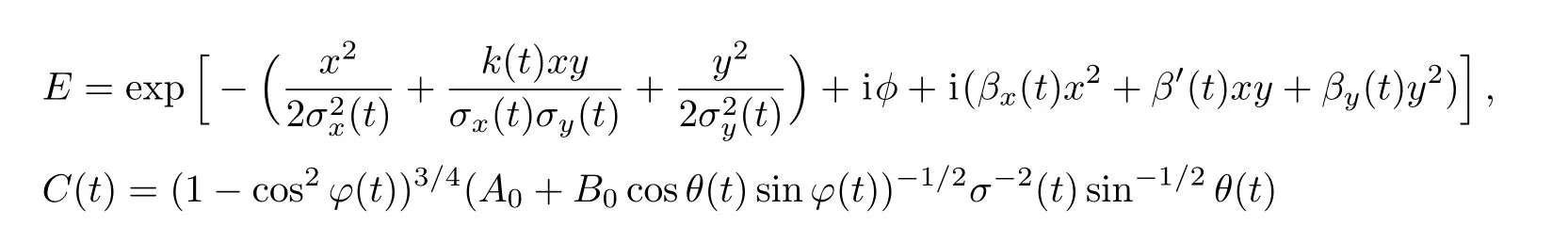
is the normalization factor with A0=4Γ(1/2)Γ(2),and B0=4Γ2(3/2).

and substituting Eq.(6c)into σxσy×Eq.(7),

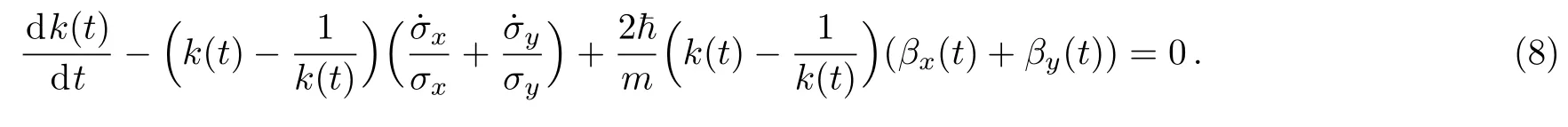
The requirement of the equation’s imaginary part being zero also puts the coefficient formula of the second asymmetric term of Eq.(6d)and Eq.(6e)to zero,which gives

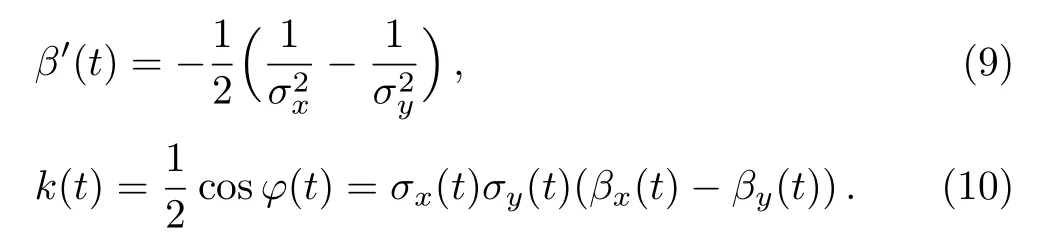
Combining Eqs.(6d)and(8)gives the first constraint formula

Using Eqs.(9)and(10),and by combining Eqs.(6a)and(6b)gives the second constraint formula

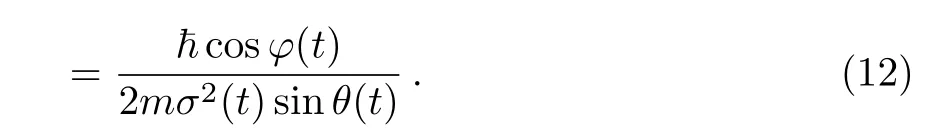
The two constraint Eqs.(11)and(12)establish θ(t)and φ(t)as functions of σ(t)

From Eq.(6),we obtain the following

After substituting Eqs.(13)and(14)into the ansatz Eq.(4),then using the Lagrangian density Eq.(3),and integrating over the spatial variables,we get

Considering the action

the Euler-Lagrangian equation

gives

The explicit form and derivation of V(σ)will be discussed in the following steps.We investigate two typical principal cases based on Eqs.(11),(12),and(16)as follows:

Case 1Equations(11)and(12)have the trivial solution cosθ(t)=cosφ(t)≡ 0.The solitary vortex solution takes the simpler form

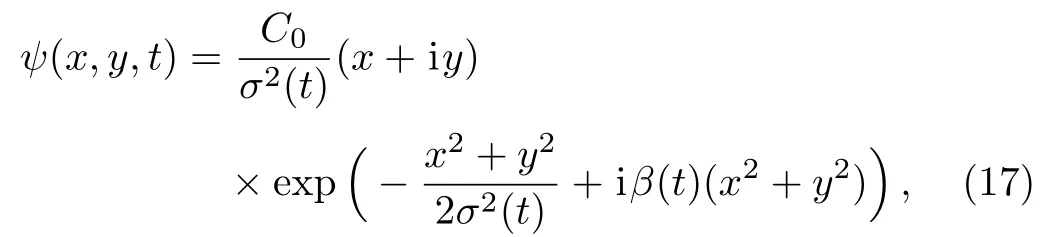
where C0is the normalization constant,and Eq.(14)with Eq.(15)give

The V(σ)in the resultant Euler-Lagrangian of Eq.(16)takes the following form

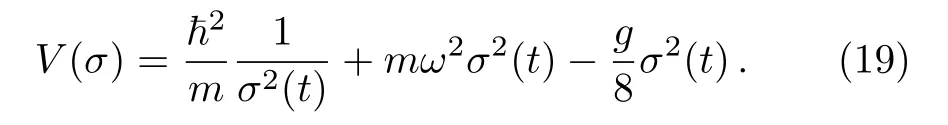
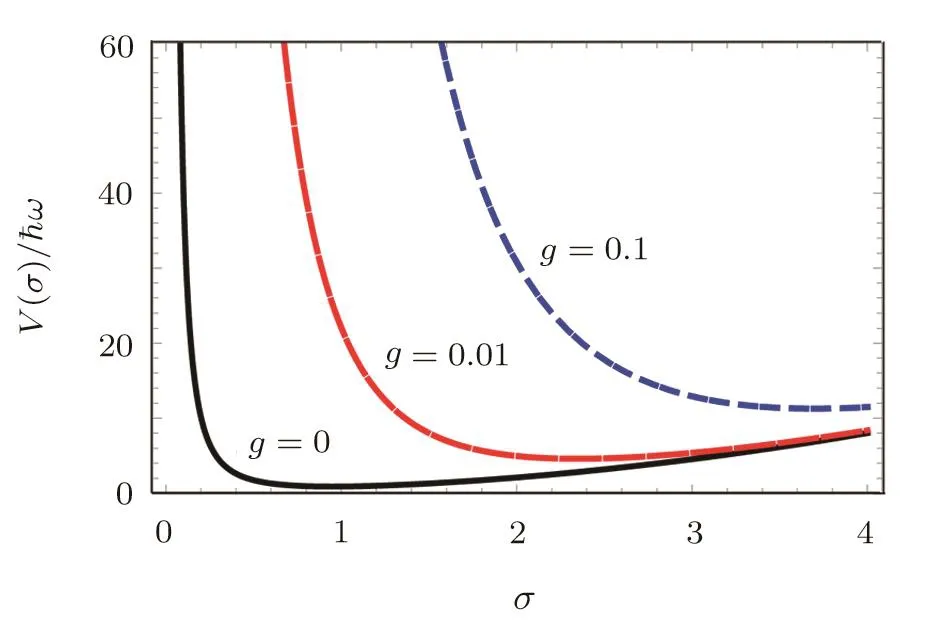
Fig.1 V(σ)vs. σ (in units offor three different nonlinear interaction constants:g=0,0.01,0.1 in units of 4πh2a0/m,and a0is the initial s-wave scattering length.

Figure 1 shows the pictorial plot of V(σ)vs. σ for three different nonlinear interaction constants g=0,0.01,0.1(in units of 4πh2a0/m,and a0is the initial s-wave scattering length).V(σ)has a minimum point σmfor the weak nonlinear interaction constant g.If the initial value of σ(t)is σ(t=0)= σ0,it is not far from the minimum location σmof V(σ),and σ(t)will oscillate around σ = σm.Whensubstituting Eq.(19)into Eq.(16),which is solvable with the following solution

where

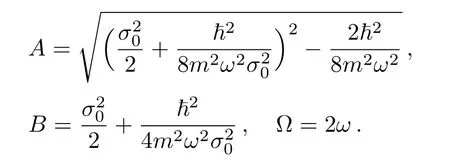
Fig.2 The two-dimensional snapshots of the solitary vortices at eight timing positions during one oscillation cycle with(a)t=0,(b)t= π/4?,(c)t= π/2?,(d)t=3π/4?,(e)t= π/?,(f)t=5π/4?,(g)t=3π/2?,and(h)t=7π/4?.

Case 2In this situation,the initial cosθ and cosφ slightly deviated from zero,and we assume σ(t)? σ0(the amplitude of oscillation for σ is close to zero,so˙σ(t)?0).The evolutions of θ(t)and φ(t)are then investigated based on the coupled Eqs.(11)and(12)(the term with˙σ vanishes),and we numerically evaluate θ(t)and φ(t)(since cos(θ(t))and cos(φ(t))can not be expressed in simple analytical forms).The solitary vortex wave function Eq.(4)is then calculate and the evolutionary patterns for the modulus of the solitary vortex wave function at four timing positions are displayed in Fig.3(based on the numerical evaluation of θ(t)and φ(t)).

The evolutionary patterns obtained for cases 1 and 2 are compared with those reported in a prior numerical study.[20?21]Comparing Fig.2 with Figs.3(b)–3(e)of Ref.[20]where the near-zero quintic nonlinearity is almost nonexistent,we identify similar cylindrical symmetric evolution pattern for the solitary vortex.Comparing Fig.3 with Fig.4(a)of Ref.[21],we observe qualitative agreements in the evolutionary features.Beyond the simple situation stipulated in case 2,a nonzero˙σ in Eq.(12)makes the detailed analytical study complex,but θ(t),φ(t),and σ(t)can be evaluated numerically,and we anticipate the evolutionary pattern that is similar to Fig.6 in prior numerical study,[22]with the combination of the periodic feature of case 1 and asymmetric feature of case 2,can be generated under appropriate setting.

Fig.3 Two-dimensional plots of the Modulus of the solitary vortex at four timing positions(at t=0,(a)t=0,(b)and(d)(the horizontal and vertical scales are in units of σ0/2).

3 Solitary Vortex with Higher Vorticity

The analytical study of a solitary vortex with vorticity S=1 can be easily generalized to an arbitrary integer vorticity S(S≥2)as follows:

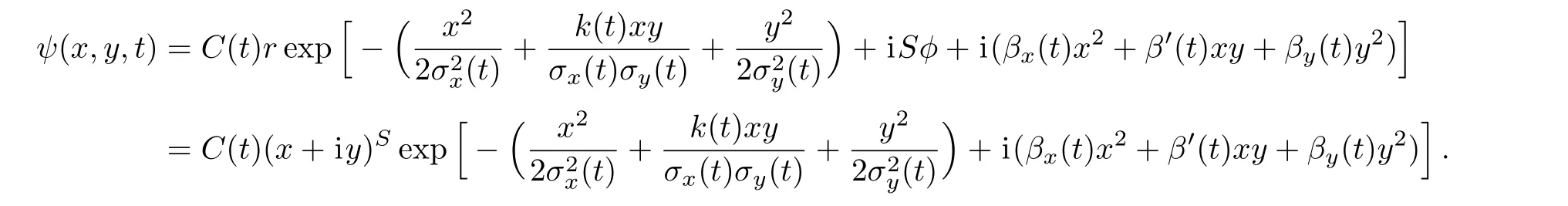
Using similar parametric functions σ(t), θ(t)and φ(t)as those for the case S=1,we anticipate a more complex analytical relationship between these three parametric functions.The evolution pattern analysis will rely more on the numerical assessment of σ(t),θ(t)and φ(t).The relatively simple S=1(or lower integer S value)case demonstrate the key features of our theoretical treatment.The derived analytical results can be used to guide the corresponding experimental investigations of vortex dynamics in two dimensional BEC systems.

4 Conclusion

In this study,for a two-dimensional Bose-Einstein condensate system in a harmonic trapping potential,we have theoretically investigated the solitary vortex evolution based on the two-dimensional GPE model and variational method.We took into account the possible inherent initial perturbations and adopted a general asymmetric variational wave function ansatz in Gaussian form.For the case with vorticity S=1,we attained the solitary vortex solution and discussed two categorical cases:the axially symmetric case that evolved into the quasi-stable pattern under certain parametric settings,and the asymmetric case arising from an initial perturbation where the solitary vortex diverged and propagated away.We pictorially demonstrated the evolutionary pattern for the two typical cases and compared these with the evolutionary pictures based on a pure numerical study and identified similar features,which demonstrated the applicability of our theoretical treatment.The analytical results presented here can be used to furnish corresponding experimental investigations of vortex dynamics in two-dimensional BEC systems.