Zheng-Yi Ma(馬正義), Jin-Xi Fei(費金喜),and Jun-Chao Chen(陳俊超)Department of Mathematics,Zhejiang Lishui University,Lishui 33000,China

2Department of Photoelectric Engineering,Zhejiang Lishui University,Lishui 323000,China

3Department of Mathematics,Zhejiang Sci-Tech University,Hangzhou 310018,China

1 Introduction

The nonlocal symmetry has two functions:(i)it can magnify the classes of symmetry.(ii)it can construct the explicit analytic solutions.Of course,there exists the intimated relation with an integral model.This model exists the nonlocal symmetry,but its explicit solution cannot be constructed easily.An ideal technical route is that we need transform the nonlocal symmetry into the related Lie point symmetry,which the similarity reduction can be calculated.So,the study of the nonlocal symmetry is significant.

Starting from the conformal invariance(Schwartz form)of an integrable model,Lou obtained infinitely many nonlocal symmetries.[1?2]Through the localization procedure of the nonlocal symmetry,which has a closed contact with the Darboux transformation(DT),Lou obtained the explicit analytic interaction solutions between the cnoidal waves and a solitary wave for some integrable nonlinear models including the well-known Korteweg-de Vries(KdV)equation.Xin devised another method to seek the nonlocal symmetries of some nonlinear evolution equations.[3?4]Its validity and advantages of the proposed method were illustrated by the applications to the Boussinesq equation,the coupled Korteweg-de Vries system,the Kadomtsev-Petviashvili equation,the Ablowitz-Kaup-Newel-Segur equation,and the potential Korteweg-de Vries equation.The conclusions showed that this method can obtain not only the nonlocal symmetries but also the general Lie point symmetries of the given equations.By means of the standard truncated Painlevé expansion,we derived the residual symmetry of several integrable models,including the(2+1)-dimensional coupled Burgers equation,(2+1)-dimensional Boiti-Leon-Pempinelli system and the Whitham-Broer-Kaup equation.[5?7]These residual symmetries were localized in the properly prolonged system with the Lie point symmetry vector.Based on the obtained symmetries,some different transformation invariances were derived.Furthermore,the reduction solutions(especially the interactive solutions)were obtained with different nonlinear excitations which closely related to some practical applications.

In order to describe two-place physical problems,Lou proposed many possible models named Alice-Bob(AB)systems.[8]The considering objects include the KdV equation,the nonlinear Schr?dinger(NLS)equation,the modified KdV equation(MKdV),the sine-Gordon(sG)equation,the(2+1)-dimensional KP equation,the Toda lattice and the difference-difference systems such as the H1,H2,H3,Q1,Q2,Q3,and Q4.[9]To solve these related AB systems,the Ps-Td-C(parity with a shift,time reversal with a delay,charge conjugation)combination technic is mainly taken.As a result,some special types of Ps-Td-C group invariant multi-soliton solutions for these AB systems are explicitly constructed.

In this paper,we have the following arrangements.In Sec.2,the nonlocal symmetry of the AB-mKdV equation is obtained with the help of its Lax pair and the assumption of the related symmetry.In Sec.3,by introducing one auxiliary variable and some reduction technics,the nonlocal symmetry is localized through the Lie point symmetry.Further more,with the aid of the prolonged system,the symmetry reduction is extended.In Sec.4,the reduction solution of the AB-mKdV system is obtained and two interaction solutions are depicted through the particular functions with numerical simulation.Section 5 proposes a simple conclusion.

2 Nonlocal Symmetry of the AB-mKdV Equation

Traditionally,the third order Ablowitz-Kaup-Newell-Segur(AKNS)system

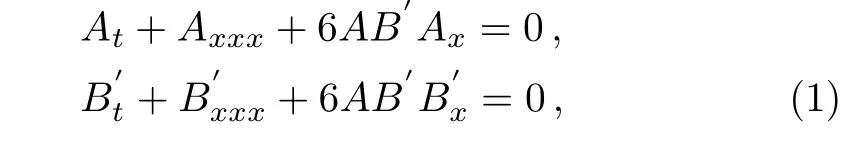
has a natural reduction

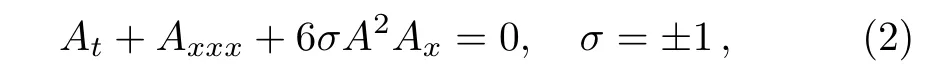
if B′= σA,which is just the well known modified Korteweg-de Vries(mKdV)equation.

For the case of B′=Bf,the above one-place coupled system(1)possesses an equivalent two-place form

As a result,an intrinsic two-place AB-mKdV equation can be derived from the two-place form(3)

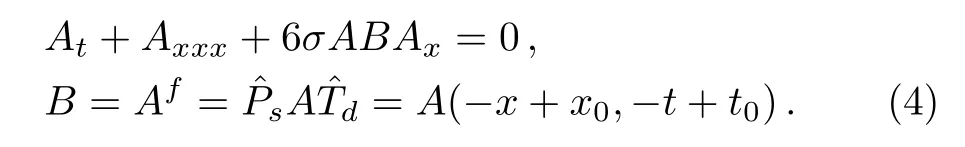
When taking x0=0 and t0=0,Ji and Zhu have investigated its Darboux transformation of this integrable nonlocal model,and obtained its different kinds of exact solutions,including soliton,kink,antikink,complexiton,rogue-wave solutions and nonlocalized solution with singularity.[10]For the AB-mKdV equation(4),Li,Lou,and Jia have constructed the Nth Darboux transformation and given its one-soliton and two-soliton solutions through this Darboux transformation,which possess some new properties that are different from the ones of the mKdV equation.[11]

In order to derive the nonlocal symmetry of the AB-mKdV equation(4),the needed Lax pair of this equation can be taken as the following explicit form,which is just the circumstance of σ =1 and λ =0 in Ref.[8]

where ψ =,and the compatibility condition of these equations is

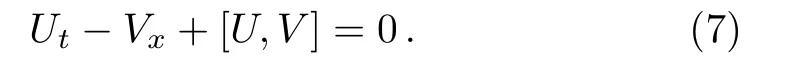
Here,a direct way that can derive the nonlocal symmetry is devised and both the classical Lie point symmetry and the nonlocal symmetry of the given equation can be acquired by this approach.

Firstly,the symmetries σ1and σ2of the AB-mKdV equation(4)can be expressed as a solution of their linear equations

which means that Eq.(4)is form invariant under the infinitesimal transformations A → A+εσ1and B → B+εσ2with the infinitesimal parameter ε.

Secondly,we suppose the symmetries σ1and σ2with the auxiliary variables ψ1and ψ2as

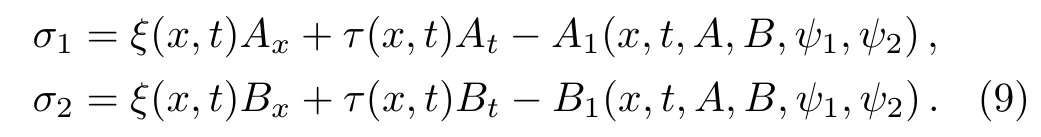
Then substituting Eq.(9)into Eq.(8),making use of the equations of the AB-mKdV equation(4)and its Lax pair(3)–(6)and eliminating At,Bt,Uψ,and V ψ,we can get the determining equations for the functions ξ,τ,A1,and B1,which can be solved by virtue of Maple software

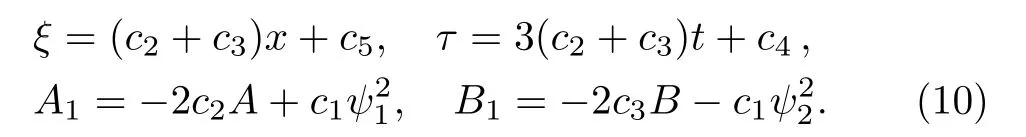
Finally,the symmetry of Eq.(4)can be rewritten as follows

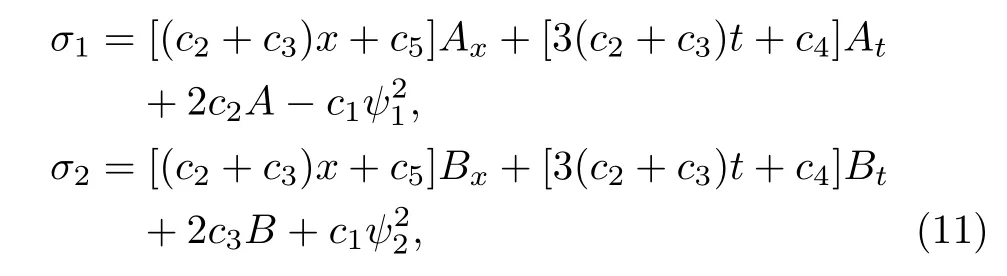
where ci(i=1,2,3,4,5)are five arbitrary constants.Here,the symmetry of Eq.(11)consists of two parts,namely,the classical symmetry

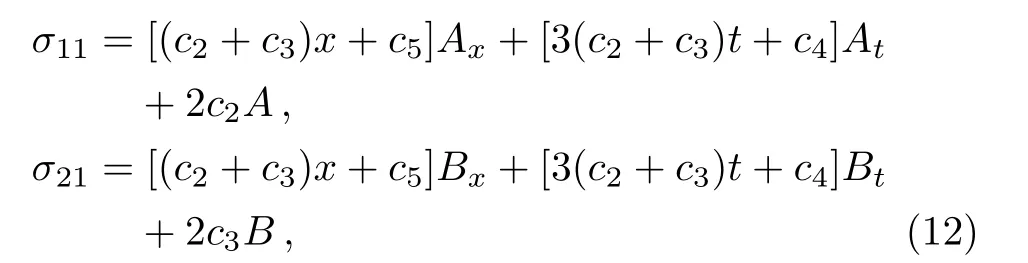
and the nonlocal symmetry

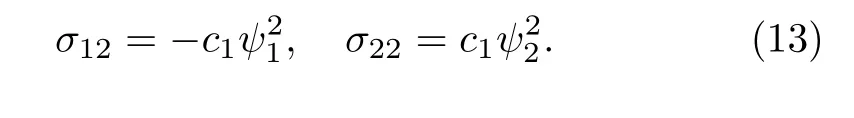
3 Localization of the Nonlocal Symmetry

Since the nonlocal symmetry cannot be used to construct the explicit solution of a partial differential equation directly,we need to transform this component to local one.In this section,we will seek for a related system which possesses a Lie point symmetry for the nonlocal symmetry.For simplicity,letting c2=c3=c4=c5=0 and c1=1,then Eq.(11)has

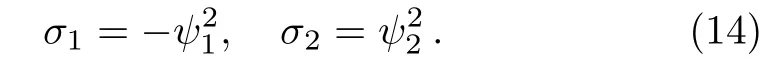
At the same time,we can obtain the linear form of Eqs.(5)and(6)respectively,under the infinitesimal transformations

That is to say,the symmetries of the Lax pair are

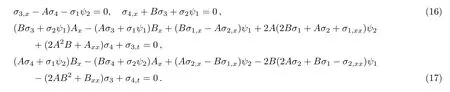
To make the nonlocal symmetry into local one,we introduce an auxiliary variable p≡p(x,t),which should satisfy

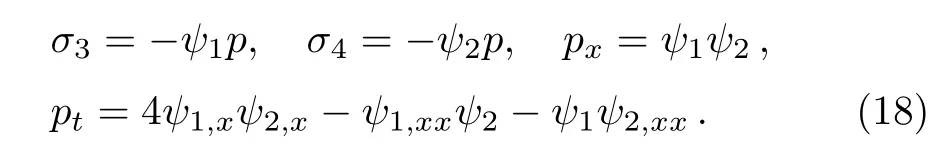
When taking the infinitesimal transformation p→ p+εσ5,we receive the symmetry from Eq.(18)

From Eqs.(14),(16)–(19),we obtain a set of symmetry solution

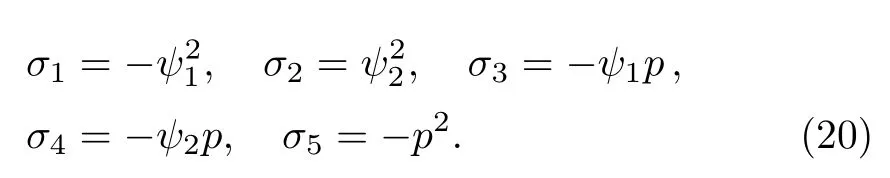
The above solution indicates that σ1= ?and σ2=have been localized in the properly prolonged system with the Lie point symmetry vector of Eq.(12),that is

Now,we have successfully obtained the localizing result.It is nature that we should construct the explicit solution through Lie group theory with the related prolonged system(21).

With the aid of the following initial condition

through the Lie point symmetry vector(21),the finite transformation is

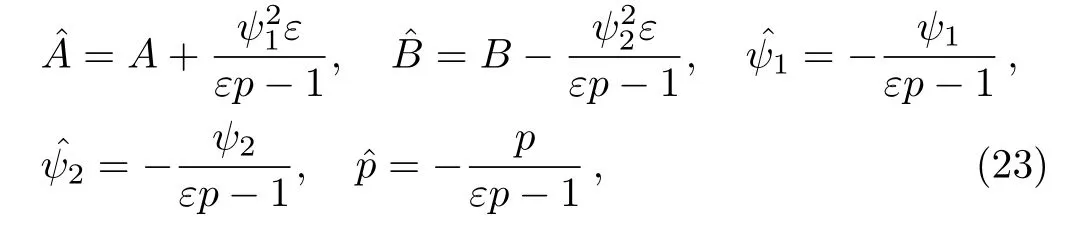
the related functions A,B,ψ1,ψ2and p are the solutions of the prolonged system(4)–(6)and(18).

To seek for more similarity reductions of Eq.(4),the whole prolonged system of Lie point symmetry instead of a single one should be researched.We suppose that the symmetry has the vector form

and the version in Eq.(24)can be written as follows

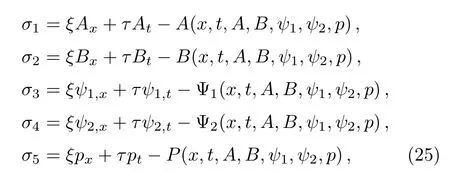
with the transformation

Substituting the prolonged system(25)into the linear equations(14),(16)–(19)and making use of Maple,we get

In this way,Eq.(25)can be rewritten as

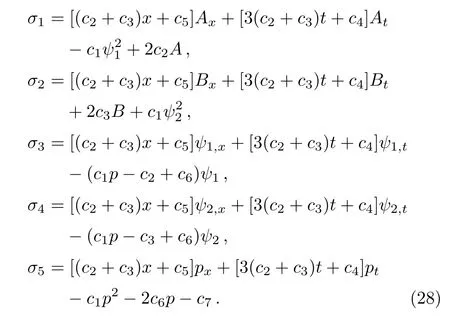
this is just the circumstance of Eq.(20)when taking the coefficients ci=0,i=2,3,...,7 and c1=1.

4 Reduction Solution of the AB-mKdV Equation

In this section,for the purpose of more invariant solutions of the AB-mKdV equation(4),we need to solve the following characteristic equation

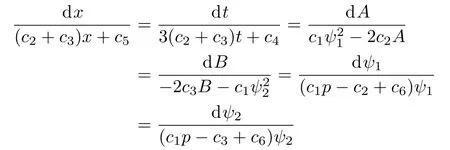
For convenience,we let c2=c3=0,c4=1 and c5=k in Eq.(29).Then,we can derive

with?=and A1(X)represent the group invariant solutions respectively.Substituting Eq.(30)into the linear equations(14),(16)–(19),we find that they are mutual compositions and yield

While the function P(X)satisfies the following condition

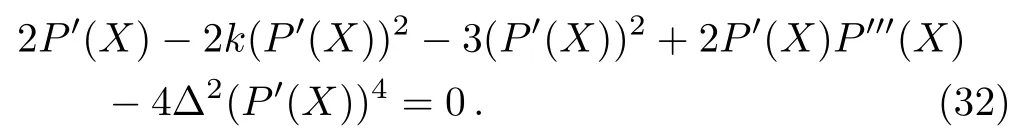
When letting P0(X)=P′(X),P0(X)is restrained by the following elliptic equation

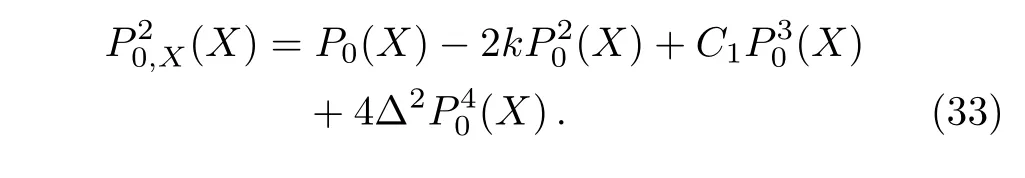
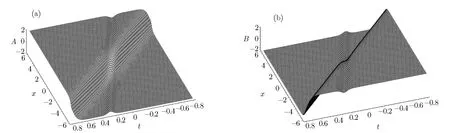
Fig.1 (a)An interaction solution between a bell soliton and a kink soliton described by A of Eq.(35)with the parameter conditions(34)when taking n=0.5,(b)the structure of solution B which is a reversal structure of(a).

To illustrate the solution A and B of Eq.(30),when taking P(X)=a0X+a1arctanh[ntanh(X)]as a direct solution of Eq.(32),the relations of the parameters are

The corresponding solution of A,B from Eqs.(30)and(31)is

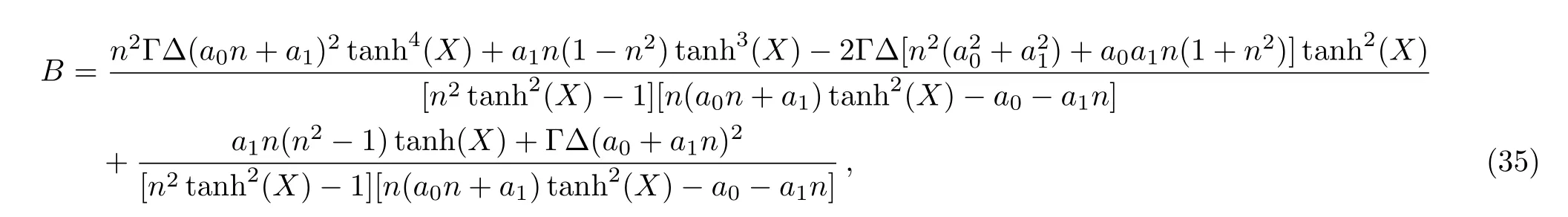
with

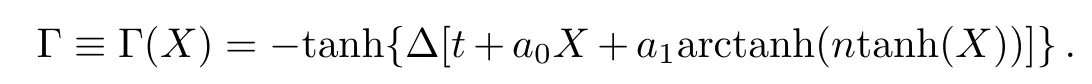
Figure 1 shows the solution A and B of Eq.(35)when taking n=0.5,the numbers a0=?0.083 333 333 32,a1=0.041 666 666 68,k=?20,and? =24 from Eq.(34).From Fig.1(a),one can find that we have a dark(gray)bell soliton and a kink soliton before the interaction.However,after the interaction,the soliton becomes a bright soliton while the kink soliton remains its shape.This kind of transition comes from the nonlocal interaction of the model for the solution A.Figure 1(b)is a reversal structure of Fig.1(a)for the solution B.

Of course,one can derive the solutions,which is different from Eq.(35). For example,when letting P(X)=a0X+a1arctanh[msn(X,m)]as a direct solution of Eq.(32),the relations of the parameters are

The corresponding solution of A,B from Eqs.(30)and(31)is

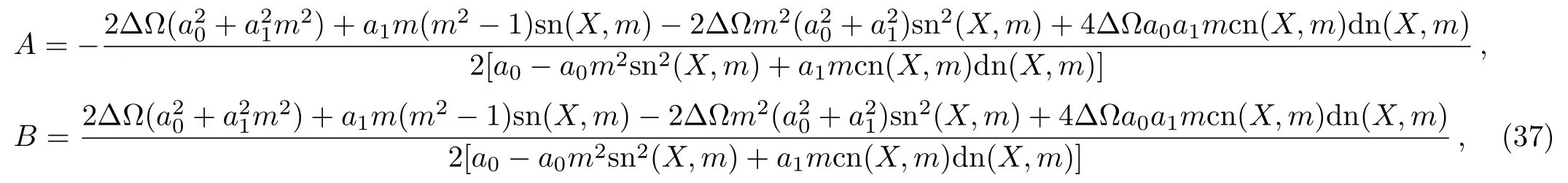
with ? ≡ ?(X)= ?tanh{?[t+a0X+a1arctanh(msn(X,m))]}.

Fig.2 (a)Profile of the solution A in Eq.(39)at the region x ∈ [?5,5],t∈ [?5,5],(b)the time t of kink-periodic section with the variable x=0,(c)the periodic section with routing display at time t=0.

In the following discussion,we let P(X)=a1EllipticPi[sn(X,m),n,m]as a direct solution of Eq.(32).The relations of the parameters are

Thus,the derived solution structure of A,B from Eqs.(30)and(31)is

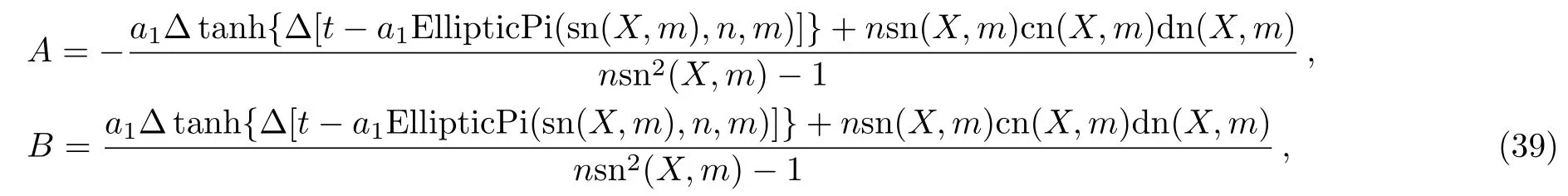
and EllipticPi expresses the incomplete elliptic integral of the third kind,three terms(sn,cn,and dn)are usual Jacobian elliptic functions with modulus m while a1and m are independent constants but the needed solution is well defined.

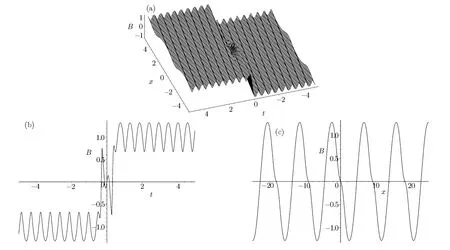
Fig.3 (a)Profile of the solution B in Eq.(39)at the region x ∈ [?5,5],t ∈ [?5,5],(b)the time t of kink-periodic section with the variable x=0,(c)the periodic section with routing display at time t=0.

When taking a1=?1/8,m=0.9,the numbers are n=0.405,k=?8.38 and? =6.170 899 448 from Eq.(38).The solution expressed by Eq.(39)is just the explicit interaction between a kink and the cnoidal periodic waves which has practical application in coastal engineering.[12?13]In Fig.2,the interaction graphs between a kink soliton and the cnoidal waves expressed by the solution A of Eq.(39)are plotted.(a)shows the whole profile at the region x ∈ [?5,5],t∈ [?5,5].We can see from this progress that a kink soliton propagating on the cnoidal waves background.(b)and(c)are the time t of kink-periodic section with the variable x=0 and the periodic section with routing display at time t=0,respectively.Figure 3 is just a reversal structure of Fig.2 for the solution B.This is just the nonlocal phenomenon,that is,“the shifted parity and delayed time reversal to describe two-place events”.

It is noted that the exact solutions(35),(37),and(39)also satisfy the relation A=?B.Recalling that the condition A=?B makes the nonlocal mKdV equation reduce to the classical mKdV equation.That is to say,although such three groups of solutions are Ps-Td-C invariant ones and satisfy the nonlocal AB-mKdV system which is used to describe two-place physical events,they are solutions of the classical mKdV equation.This fact suggests that some solutions of integrable AB systems with Ps-Td-C symmetry invariance can be directly obtained from ones of traditional integrable systems.

5 Conclusion

In this article,on the basis of the assumption of the symmetry,we gained the nonlocal symmetry of the AB-mKdV system.One auxiliary variable described asrespectively,was introduced in the process of localization.Using this method,we obtained the explicit solution of the AB-mKdV system and increased the adaptation of this system.

It is noteworthy that the finding of the suitable auxiliary variable has certain difficulty and it is key to obtain the similarity solution.Besides,not all the nonlocal symmetries have the closed prolongation and there is not a unified method to estimate what kinds of nonlocal symmetries can be spread to the Lie point symmetries of a related prolonged system.So,the above two questions are still opened.

[1]S.Y.Lou,J.Phys.A:Math.Phys.30(1997)4803.

[2]S.Y.Lou and X.B.Hu,J.Phys.A:Math.Gen.30(1997)L95.

[3]X.P.Xin and Y.Chen,Chin.Phys.Lett.30(2013)100202.

[4]X.P.Xin,J.C.Chen,and Y.Chen,Chin.Ann.Math.B 35(2014)841.

[5]Z.Y.Ma,J.X.Fei,and Y.M.Chen,Appl.Math.Lett.37(2014)54.

[6]Z.Y.Ma,J.X.Fei,and X.Y.Du,Commun.Theor.Phys.64(2015)127.

[7]J.X.Fei,Z.Y.Ma,and W.P.Cao,Nonlinear Dyn.88(2017)395.

[8]S.Y.Lou,arXiv:math-ph/1603.03975(2016).

[9]V.E.Adler,A.I.Bobenko,and Y.B.Suris,Commun.Math.Phys.233(2003)513.

[10]J.L.Ji and Z.N.Zhu,Commun.Nonlinear Sci.Numer.Simulat.42(2017)699.

[11]C.C.Li,S.Y.Lou,and M.Jia,arXiv:mathph/1706.08178(2017).

[12]Y.H.Wang,Appl.Math.Lett.38(2014)100.

[13]Y.H.Wang and H.Wang,Phys.Scr.89(2014)125203.