Meng-Yao Zhang(張夢瑤),Chao-Yun Long(龍超云), and Zheng-Wen Long(隆正文)

College of Physics,Guizhou University,Guiyang 550025,China

1 Introduction

The study of exactly solvable potentials has attracted much interest since the early development of quantum mechanics because the explicit expressions for the eigenvalues and eigenfunctions give a better insight into the detailed properties of a dynamical system.[1]Apart from time-independent quantum system,the time-dependent quantum problems raised considerable interest since the work of Lewis and Riesenfeld.[2?9]The analytical solutions of the time-dependent Schr?dinger equation are not only of physical importance but also of theoretical interest because their quantum correspondence provides fundamental structure of basic physics and interpretation of new physics in different areas of physics,such as,gravitation,[10]quantum optic,[11?12]the Paul trap[13?15]and spintronics.[16]In the past few decades,an extensive effort has been made to obtain the exact solution of the time-dependent Schr?dinger equation and Dirac equation[17?21]making use of different methods,for example path integral,[22?24]invariant theory,[25?27]unitary transformation approach,[28?29]and Lie-algebraic.[30?31]On the other hand,the modification of the standard Heisenberg algebra has obtained a growing attention recently.[32?40]Such interest was motivated by the investigations in various approaches to Quantum Gravity[41?43]and black hole physics.[44]Within the GUP framework,almost all physical system with a well-defined quantum Hamiltonian is modified,near the Planck scale.In the past few years,a large amount of research work has been devoted to the study of quantum gravitational corrections to various quantum phenomena such as the Landau levels,[45]the Lamb shift,[46]phase shifts,[47]black hole entropy,[48]Hawking temperature,[49]the tunneling current in a scanning tunneling microscope,[50]and quantum phase transitions.[51]

In spite of a large variety of papers that have been published concerning time-dependent quantum systems and modification quantum systems separately,to the best of our knowledge,few works have been done on the timedependent quantum problems under the GUP.In this paper,we are interested in the time-dependent Dirac equation under the GUP which implies the existence of a minimum measurable length and a maximum measurable momentum.[52?58]It is possible to construct the exact solutions of Dirac equation for some special conditions satis fied by time-dependent potential in(1+1)dimensions.The paper is organized as follows:In Sec.2,the timedependent Dirac equation under the GUP is studied.In Sec.3,we obtain the analytical wave functions for the two kinds special time-dependent potentials in(1+1)dimension.Section 4 is our conclusions.

2 Time-Dependent Dirac Equation under the GUP

In the minimal length and maximal momentum formalism,the generalizations of the uncertainty principle is given by[53?58]

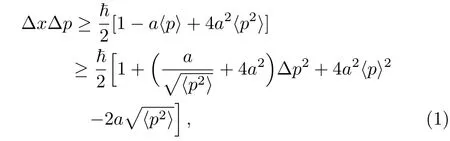
where a is the GUP parameter.According to the standard methods,the above inequality follows from the modified Heisenberg algebra

It is notice that if the parameter a is taken to be equal to zero,we obtain Heisenberg algebra of usual quantum mechanics.However,the above algebra does not admit of a simple representation in position space.So if we define

it can be shown that Eq.(2)is satis fied to order a.Here,p0ican be interpreted as the momentum at low energies,and pias that at higher energies.

Now let us begin with the(1+1)-dimensional Dirac equation with time-dependent potential in the presence of generalized uncertainty principle

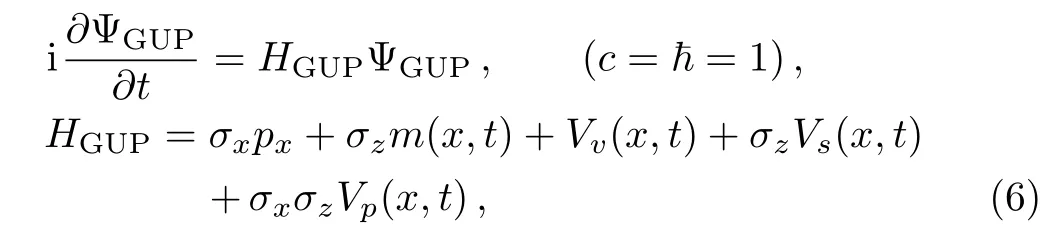
where σxand σzare two 2 × 2 standard Pauli matrices and the subscripts for the terms of potential denote their properties under a Lorentz transformation:V for the time component of the two-vector potential,S and P for the scalar and pseudoscalar terms,respectively.[20]In this way ΨGUPis a two-component spinor.

Incorporating the GUP corrections,the modified Hamiltonian in Eq.(6)becomes

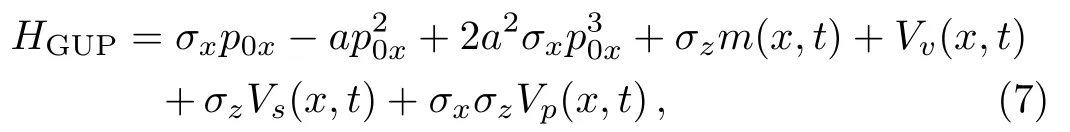
where we have used the relation(σxp0x)2=.It is easy to find that the second term and third term will disappear when the GUP is not considered(a=0).The equation(6)will be reduced to the equation considered in literature.[20]We make the more general Ansatz

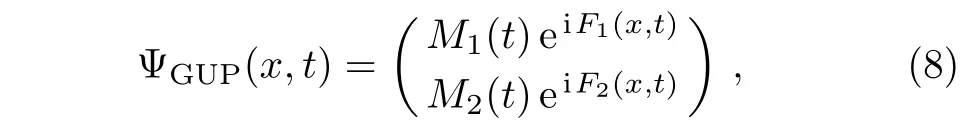
where M1(t),M2(t),F1(x,t),and F2(x,t)are four undetermined functions.Substituting Eqs.(7)and(8)into Eq.(6),we have

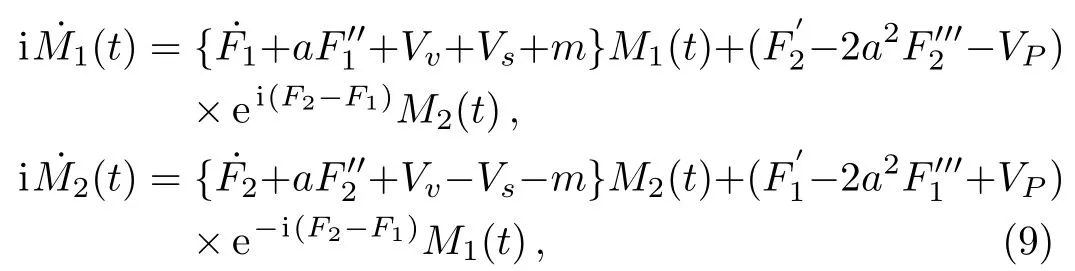
where the prime denotes differentiation with respect to x and dot with respect to t.It is worth mentioning that it is also difficult to obtain the analytic solutions of Eq.(9)because of the existence of exponential factor.In order to get rid of exponential factor in the above equations and to get the corresponding exact solutions,we impose that F1=F2,+aF′′+Vv=0,F′?2a2F′′′=0,VS+m=0.Then Eq.(9)becomes

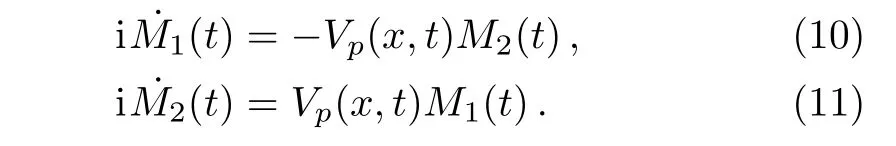
It is worth noting that due to the M1(t)and M2(t)being independent of x,in order to make Eqs.(10)and(11)hold,the factor Vp(x,t)must be independent of x.From now on,let us suppose that Vp(x,t)is just a function of time Vp(x,t)=Vp(t).Then from above decoupled equations(10)and(11)it is easy to get the following secondorder equations:

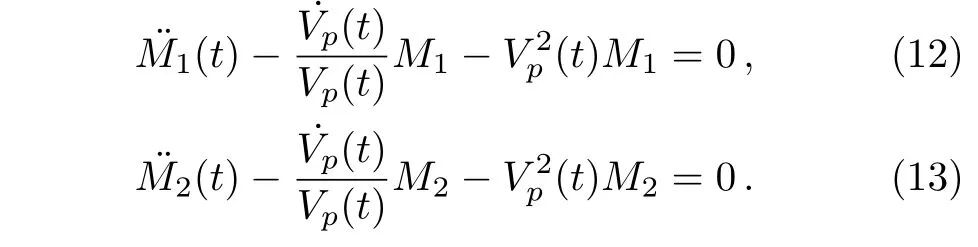
In this work,our main task is to solve Eqs.(12)and(13)for different potential Vp(t).Taking account of Eqs.(12)and(13)having same form,only one equation is considered in this article.It is worth mentioning that in general,it is also difficult to obtain analytic solutions for the Eqs.(12)and(13).In the following section of the article,we will obtain the exact solution for the two special different potential functions Vp(t).

3 Solution of Time-Dependent Dirac Equation under the GUP

Case 1

Now let us take the potential Vp(t)in form

where θ is a constant.Substituting the expression(14)into Eq.(12)yields following equation

Introducing new variable s=e?θt,we have

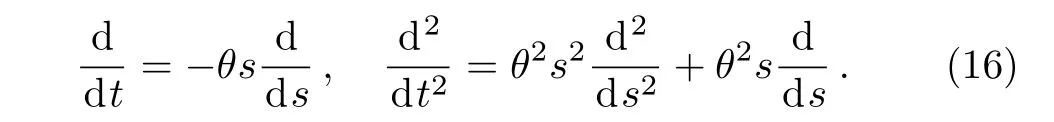
In new variable,Eq.(15)can be written as

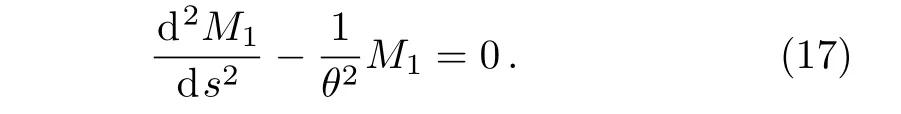
Above equation is nothing but second order linear differential equation with constant coefficient and the corresponding solution is

where α =1/θ,A1and A2are two constants.With the help of Eq.(10)we can obtain

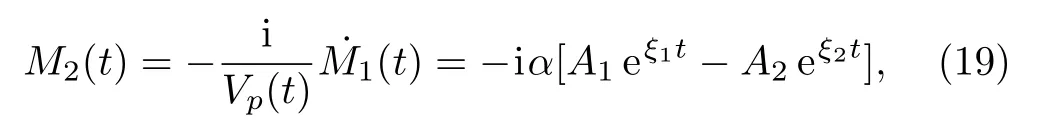
where

Finally the total wave function can be written as

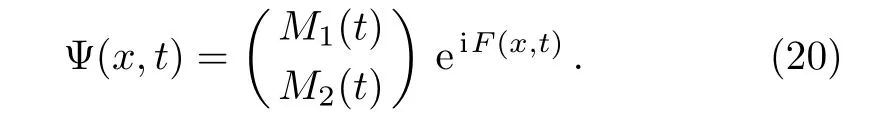
It is worth pointing out that so far F(x,t)in solution Ψ(x,t)is an undetermined function of time and position.Now letting F(x,t)=f(t)g(x)and using the precedent assumption condition F′? 2a2F′′′=0,it is straightforward to obtain the expression of function F(x,t)

Furthermore,from the assumption condition˙F+aF′′+Vv=0,it is also not difficult to find the expression of potential function Vv(x,t):

In Eq.(22),the divergence of potential function Vv(x,t)can be avoided for a=0 if the undetermined function f(t)is taken as an appropriate function.

Case 2

We make the potential Vp(t)being of the following form

Putting Eq.(23)into Eq.(12),we have the following second-order equation

The solution of Eq.(24)can be given by the asymptotic iteration method(AIM),which is a powerful method to obtain energy eigenvalues and wave functions.[59?61]AIM is proposed and applied to solve the second-order differential equations of the form

where the λ0(t)and s0(t)are sufficiently differentiable with respect to t. Based on the asymptotic iteration method,if for sufficiently large n we can obtain

where

which are called recurrence relations,the general solution of differential Eq.(24)can be written as

where C1and C2are two constants.

Making use of the recurrence relations(27)and(28),it is immediate to find θ(t)= ?1/t for Eq.(24).In consideration of taking proper integral constant,from expression(29)we can get the solution of differential equation(24):

where c is a constant.It is very easy to prove that result given in Eq.(30)satis fies Eq.(24).With the help of Eq.(10)we can obtain

Similar to the case 1,for the potential Vp(t)=λ/t,the expression of potential function Vv(x,t)can be written as

4 Conclusions

In this work the time-dependent Dirac equation is investigated under generalized uncertainty principle(GUP)framework.It is worth noting that in general,it is difficult to obtain analytic solutions for the time-dependent Dirac equation under the GUP because of the existence of exponential factor in the wave equation.However,it is possible to get rid of the exponential factor and to construct the exact solutions for proper condition satis fied by time-dependent potential.In this work,the analytical wave functions have been obtained for the two special different potential functions Vp(t).In addition the low energy excitations of charge carriers in grapheme are similar to massless relativistic Dirac particles.The grapheme provides a new and unexpected bridge between condensed matter and high-energy physics.[62]So it is also interesting to study the time-dependent Dirac particles in grapheme.

[1]Y.Bouguerra,A.Bounames,M.Maamache,and Y.Saadi,J.Math.Phys.49(2008)4859.

[2]G.Fiore and L.Gouba,J.Math.Phys.52(2011)1976.[3]H.R.Lewis,J.Math.Phys.9(1968)1976.

[4]N.J.Gunther and P.G.L.Leach,J.Math.Phys.18(1977)572.

[5]M.Kleber,Phys.Rep.236(1994)331.

[6]C.I.Um,K.H.Yeon,and T.F.George,Phys.Rep.362(2002)63.

[7]M.Maamache,J.Phys.A 31(1998)6849.

[8]M.Maamache and H.Bekkar,J.Phys.A 36(2003)L359.

[9]D.X.Macedo and I.Guedes,J.Math.Phys.53(2012)6224.

[10]S.A.Fulling,Aspects of Quantum Fields in Curved Space,Cambridge University Press,Cambridge(1982).

[11]G.S.Agarwal and S.A.Kumar,Phys.Rev.Lett.67(1991)3665.

[12]H.P.Yuen,Phys.Rev.A 13(1976)2226.

[13]L.S.Brown,Phys.Rev.Lett.66(1991)527.

[14]W.Paul,Rev.Mod.Phys.62(1998)531.

[15]M.Feng,K.Wang,J.Wu,and L.Shi,Phys.Lett.A 230(1997)51.

[16]X.F.Wang,P.Vasilopoulos,and F.M.Peeters,Phys.Rev.B 65(2002)165217.

[17]J.Q.Shen,Phys.Rev.A 63(2003)034102.

[18]M.Maamache and H.Choutri,J.Phys.A 33(2000)6203.

[19]H.G.Oh,H.R.Lee,T.F.George,and C.I.Um,Phys.Rev.A 39(1989)5515

[20]A.S.D.Castro and A.D.S.Dutra,Phys.Rev.A 67(2003)785.

[21]I.Guedes,Phys.Rev.A 68(2003)016102.

[22]I.Sokmen,Phys.Lett.A 115(1986)249.

[23]S.N.Storchak,Phys.Lett.A 161(1992)397.

[24]K.Kaneko,Phys.Rev.C 30(1984)723.

[25]H.R.Lewis and W.B.Riesenfeld,J.Math.Phys.10(1969)1458.

[26]X.C.Gao,J.Fu,J.Xu,and X.Zou,Phys.Rev.A 59(1999)55.

[27]J.Q.Shen,H.Y.Zhu,and P.Chen,Eur.Phys.J.D 23(2003)305.

[28]M.Maamache,J.Math.Phys.39(1998)161.

[29]M.A.Lohe,J.Phys.A:Math.Theor.42(2008)035307.[30]C.F.Lo,Eur.Phys.J.B 84(2011)131.

[31]C.F.Lo,Europhys.Lett.39(1997)263.

[32]M.I.Samar and V.M.Tkachuk,J.Math.Phys.57(2016)407.

[33]H.Hassanabadi,S.Zarrinkamar,and E.Maghsoodi,Phys.Lett.B 718(2012)678.

[34]P.Pedram,K.Nozari,and S.H.Taheri,J.High Energy Phys.1103(2011)093.

[35]A.F.Ali,M.Faizal,and M.M.Khalil,J.High Energy Phys.1412(2014)159.

[36]A.F.Ali,M.Faizal,and M.M.Khalil,Nucl.Phys.B 894(2015)341.

[37]M.Faizal and B.Pourhassan,Phys.Lett.B 751(2015)487.

[38]J.P.Bruneton and J.Larena,Gen.Relat.Gravit.49(2017)56.

[39]S.Das,E.C.Vagenas,and A.F.Ali,Phys.Lett.B 690(2010)407.

[40]S.Das and R.B.Mann,Phys.Lett.B 704(2011)596.

[41]K.Konishi,G.Paffuti,and P.Provero,Phys.Lett.B 234(1990)276.

[42]M.Maggiore,Phys.Lett.B 304(1993)65.

[43]A.Kempf,Phys.Rev.D 54(1996)5174.

[44]P.Meade and L.Randall,J.High Energy Phys.05(2012)2008.

[45]A.F.Ali,S.Das,and E.C.Vagenas,Phys.Rev.D 84(2011)741.

[46]C.H.T.Wang,R.Bingham,and J.T.Mendonca,Am.Inst.Phys.Conf.Ser.1412(2010)203.

[47]K.C.Littrell,B.E.Allman,and S.A.Werner,Phys.B 241(1997)1219.

[48]L.Susskind and J.Uglum,Phys.Rev.D 50(1994)2700.

[49]R.Banerjee,C.Kiefer,and B.R.Majhi,Phys.Rev.D 82(2010)2105.

[50]S.Das and E.C.Vagenas,Phys.Rev.Lett.101(2008)221301.

[51]E.Elizalde and S.D.Odintsov,Mod.Phys.Lett.A 8(1992)3325.

[52]S.Masood,M.Faizal,Z.Zaz,et al.,Phys.Lett.B 763(2009)218.

[53]S.Deb,S.Das,and E.C.Vagenas,Phys.Lett.B 755(2016)17.

[54]A.F.Ali,S.Das,and E.C.Vagenas,Phys.Lett.B 678(2009)497.

[55]H.Hassanabadi,S.Zarrinkamar,and A.A.Rajabi,Phys.Lett.B 718(2013)1111.

[56]S.Haouat,Phys.Lett.B 729(2014)33.

[57]A.F.Ali,J.High Energy Phys.2012(2012)1.

[58]P.Pedram,Phys.Lett.B 702(2011)295.

[59]H.Ciftci,R.L.Hall,and N.Saad,J.Phys.A 36(2003)11807.

[60]A.Soylu,O.Bayrak,and I.Boztosun,J.Math.Phys.51(2010)4789.

[61]H.Ciftci,R.L.Hall,and N.Saad,J.Phys.A 38(2005)1147.

[62]M.A.H.Vozmediano,M.I.Katsnelson,and F.Guinea,Phys.Rep.496(2010)109.