Constructions for almost perfect binary sequence pairs with even length
PENG Xiuping,LIN Hongbin,REN Jiadong,and CHEN Xiaoyu
1.School of Information Science and Engineering,Yanshan University,Qinhuangdao 066004,China;2.School of Electrical Engineering,Yanshan University,Qinhuangdao 066004,China;3.Hebei Key Laboratory of Information Transmission and Signal Processing,Yanshan University,Qinhuangdao 066004,China
1.Introduction
The perfect sequence is the optimal signal for communication system,telemetry,synchronization,fast start-up equalization,or stream-cipher system[1].However,perfect binary sequences with length T>4 and perfect quadriphase sequences with length T>16 have been not known until now[2,3].Therefore,almost perfect sequences have attracted more and more attention and have been applied successfully to the extremely low power over the-horizon(OTH)radar[4].Wolfmann in[5] firstly studied almost perfect binary autocorrelation sequences and got some almost perfect binary sequences with period T≤100 searching by the computer.Pott established the relationship between almost perfect binary sequences and some certain divisible difference sets(DDSs)and verified the existence of almost perfect binary sequences by applying known theorems on DDSs in[6].The numbers of almost perfect sequences have greatly increased when compared to the perfect sequences,but there are still some shortcomings,such as the length of the almost perfect binary sequence must be a multiple of 4.And there are six types of length within 100 that still do not exist[7].
To overcome this obstacle,a new type of discrete signal was studied as a binary sequence pair in[8].The new signal is a special type of mismatched filtering.All the filter coefficients are integers that can simplify the implementation and may have a good balance property.
Given a binary sequence u=(u(t)with length T,where u(t)∈{1,-1}.The set D is the characteristic set of u when D={0≤t<T:u(t)=1}.The sequence u is a balanced binary sequence in condition of|D|=T/2 for even T or|D|=(T±1)/2 for odd T,where|D|denotes the cardinality of D or the weight of sequence u.
Given a binary sequence pair(u,v)with length T,the two valued periodic correlation function of(u,v)is defined as
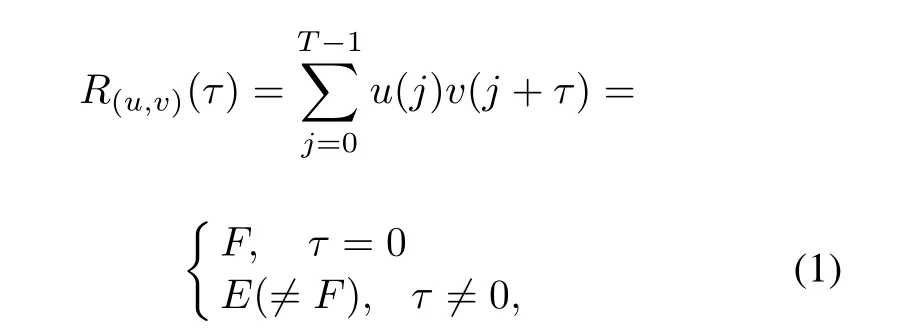
where F and E are the in-phase and out-of-phase correlation values of(u,v)respectively.When E=0,(u,v)is considered to be a perfect binary sequence pair.The concept of the perfect binary sequence pair was first proposed in[8]and some constructions were presented in[9].Subsequently,in[10],it was conjectured that the perfect binary sequence pair was limited to the length of T≡0(mod4)and in-phase correlation value|F|=4.Therefore,the almost perfect binary sequence pair was discussed in[7].
Given a binary sequence pair(u,v)with length T,the almost perfect binary sequence of(u,v)is defined as
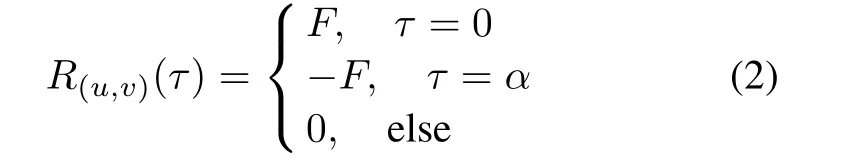

Table 1 Summary of known binary sequence pairs with optimal out-of-phase correlation values
In this paper,some new types of almost perfect binary sequence pairs of length T=2q are presented,where q is any odd number.Thus several new kinds of DDSPs are derived.
2.Preliminaries
2.1DDSP
Definition 1[7] Let D = {di|1≤i≤ m}and D′={|1 ≤ i≤ m′}be two subsets of ZTwith m and m′elements respectively.Given a nonzero subset H with n elements of ZT.Then(D,D′)is considered as a(T/n,n,m,m′,λ1,λ2)-DDSP for the condition of{di-:di∈ D,∈ D′,di/=}containing each nonzero element of H exactly λ1times and each element of ZT?/H exactly λ2times,where the set Z?/H is formed by the elements that are present in Z?but not in H.If D=D′,the DDSP is called a DDS.
Lemma 1[7]Given a DDSP(D,D′)whose parameters are(T/n,n,m,m′,λ1,λ2)of ZT,then it holds that
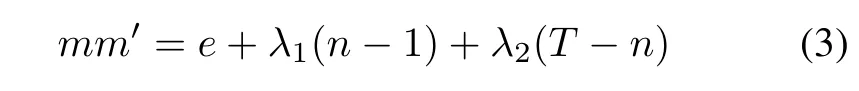
where e=|D∩D′|.
Lemma 2[7] Given a DDSP(D,D′)with parameters(T/n,n,m,m′,λ1,λ2)ofZT.andbe two characteristic sequences of sets D and D′respectively.Then
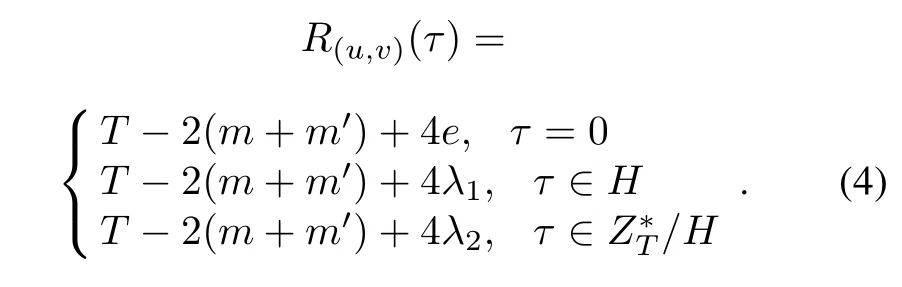
2.2 Binary ideal sequences
A binary sequence is called the ideal binary sequence when all the out-of-phase correlation values are-1.The known four classes of binary ideal sequences are listed as follows[16].
(i)T=2n-1,n positive integers(The detailed information about this type of sequence can be referred to[16]);
(ii)T=q(q+2):twin-prime sequences,both q and q+2 are primes;
(iii)T=q:Legendre sequences,q is a prime;
(iv)T=4s2+27:Hall sequences,T is a prime.
2.3 Legendre sequences
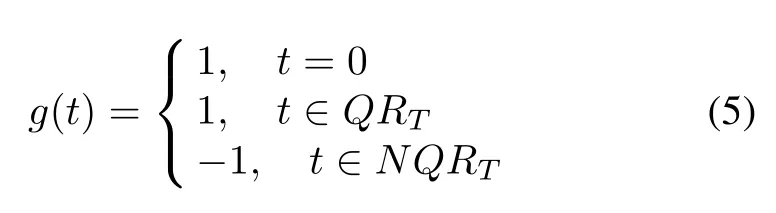
where QRTand NQRT=QRTare the sets of quadratic residues and quadratic nonresidues modulo N respectively.And the other type of Legendre sequencewith length T is defined by
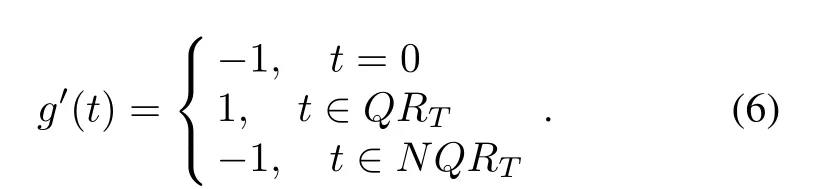
The cross-correlation properties of the two types of Legendre sequences g and g′(or g′and g)are listed in the following Lemma 3.
Lemma 3[16]When T≡1(mod4)is an odd prime and for 0≤τ≤T-1,we have
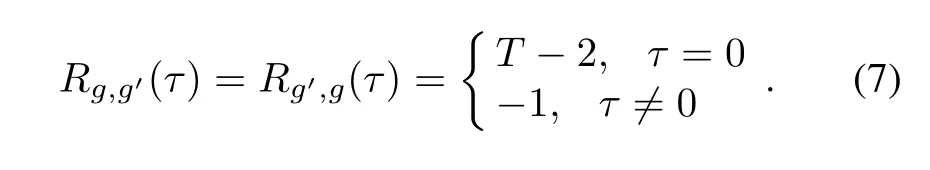
3.Main results
Two new classes of almost perfect binary sequence pairs of length T=2q,where q is an odd number,will be presented in this section.
Construction 1Give a binary sequence
with length q.Two matricesA=(aj,k)andB=(bj,k),where j=0,1 and 0≤k≤q-1,are defined as
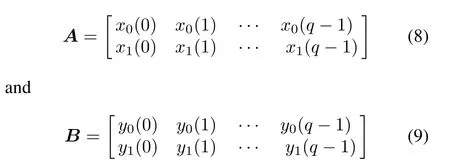
where xj(t)and yj(t)are determined by the sequence s=or other sequence by some rule which will soon follow.The sequencesandare defined by

and

where
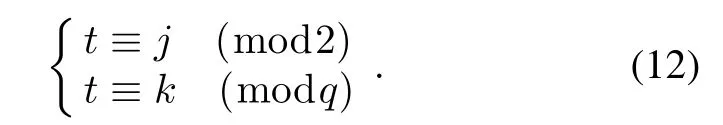
The constructions of almost perfect binary sequence pairs(u,v)with period N=2q are described in the following theorems and corollary.
In this paper,we assume that(-1)qis the sequence with all the elements being–1 and length q.
3.1 Based on binary ideal sequence
Theorem 1Given an ideal binary sequence s with length q≡3(mod4)and weight(q+1)/2.The line sequences xj(t)ofAand yj(t)ofBare defined as
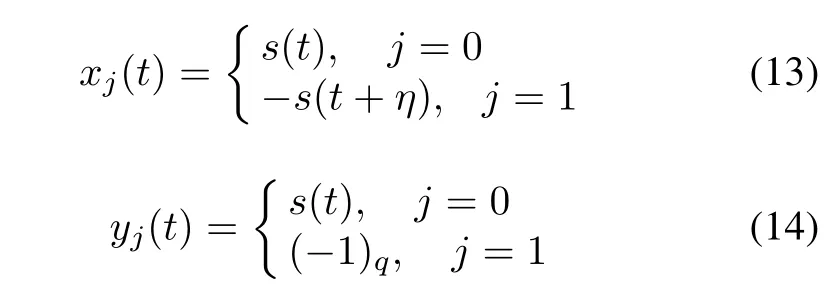
for 0≤t≤q-1,where j=0,1 and 0≤η≤q-1 is any fixed integer.Then the sequence pair(u,v)obtained in Construction 1 is an almost perfect binary sequence pair of length 2q.The correlation is given as
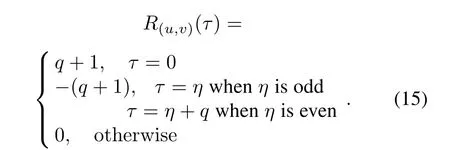
ProofSince gcd(2,q)=1,we get Z2q~=Z2×Zq.For any τ=(τ1,τ2),
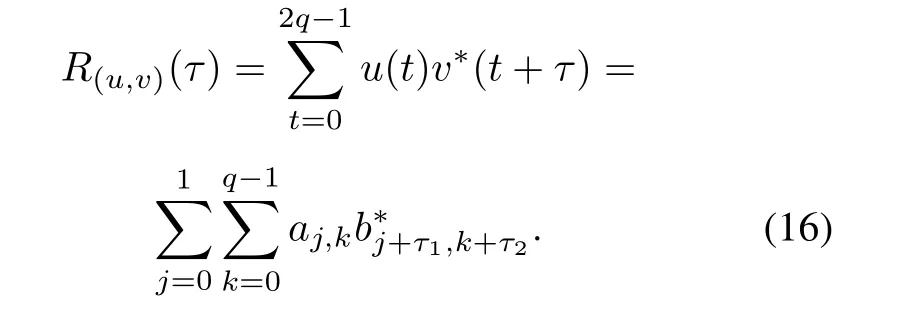
Thus we calculate the value of R(u,v)(τ)in the following two cases.
(i)For τ1=0 and τ2≡ 0(modq)
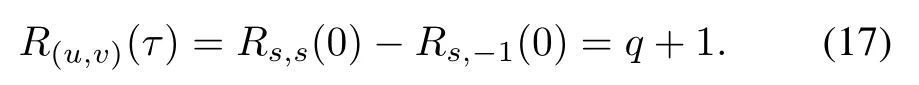
(ii)For τ1=1,R(u,v)(τ)is calculated by

When τ2- η ≡ 0(modq),we can get τ2≡ η (modq)and τ=(1,τ2)=(1,η).For η being an odd integer,it is known that τ= η;for η being an even integer,we get that τ=η+q,and obtain
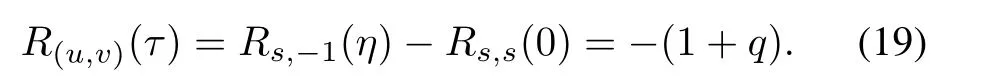
When τ2- η/=0(mod q),R(u,v)(τ)is calculated as

Theorem 1 is proved by summarizing the above two cases. □
Theorem 2Give two characteristic sets D and D′of the constructed sequences u and v in Theorem 1 respectively.Let C be the characteristic set of the underlying sequence s.Then(D,D′)is a DDSP with parameters of?
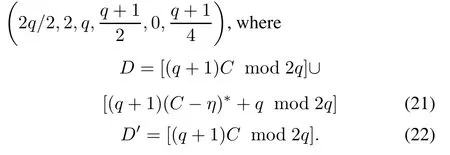
Furthermore,
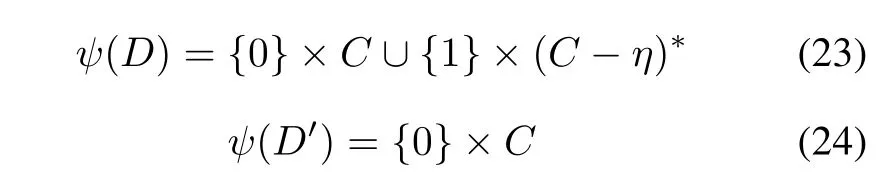
where(C-η)?denotes the complement of(C-η)in Zqand ψ(t)=(t mod 2,t mod q)is the isomorphism from Z2qto Z2×Zq.
ProofSince s is a binary ideal sequence with weight(q+1)/2,it is easy to obtain that the period of s must be q≡3(mod 4).We can get 4p+(-1)q=1 assuming that q=4p-1 for any integer p.By the Chinese remainder theorem described in[17],(12)holds if and only if
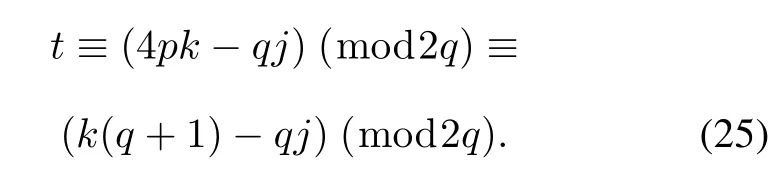
According to the sequences u and v constructed in Theorem 1 and matricesAandBdefined in Construction1,the conclusion in(21)–(24)can be obtained.
It is easily obtained that
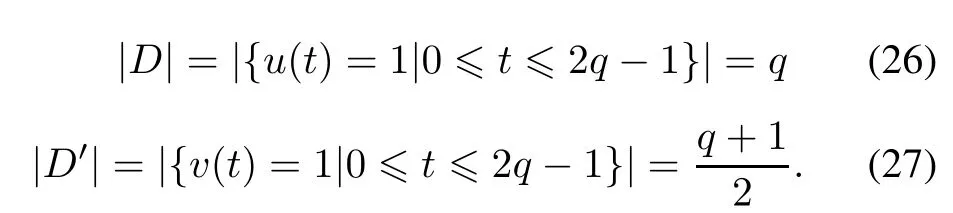
From Lemma 1 and Lemma 2,we obtain that(D,D′)is a DDSP with parameters of
Example 1Give an ideal binary sequence s =(-1,-1,1,-1,1,1,1).Let η=3.Then an almost perfect binary sequence pair(u,v)constructed in Theorem 1 with length 14 is expressed as
u=(-1,-1,1,-1,1,1,1,1,-1,-1,-1,1,1,-1),v=(-1,-1,1,-1,1,-1,1,-1,-1,-1,-1,-1,1,-1).
Their correlation values are expressed as

The characteristic sets(D,D′)obtained in Theorem 2 is listed as
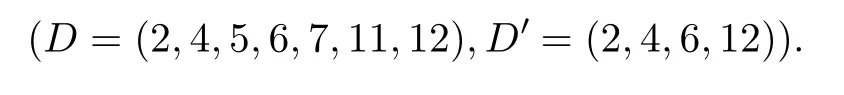
The sets are a(14/2,2,7,4,0,2)-DDSP since
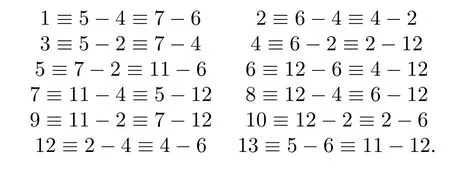
The element{11}is presented 0 time and each nonzero element of Z14/{0,11}has exactly two representations,and|D|=7,|D′|=4.
The construction of almost perfect binary sequence pairs with length 2q in Theorem 1 and that of DDSPs of Z2qin Theorem 2 are quite general and flexible.New underlying sequences will introduce new types of almost perfect binary sequence pairs and DDSPs.
Theorem 3Theorem 1 provides four types of almost perfect binary sequence pairs of length T as the following four cases.
(i)T=2(2n-1),n≥2 is any integer;
(ii)T=2q(q+2),q and q+2 are any twin primes;
(iii)T=2q,q≡3(mod4)is any prime;
(iv)T=2q,q=4s2+27 is any prime.
Theorem 4The almost perfect binary sequence pairs obtained in Theorem 3 can induce four types of DDSPs with the parameters as follows:
(i)(2(2n-1)/2,2,2n-1,2n-1,0,2n-2)-DDSP,n≥2 is any integer;
ProofIt is easy to obtain from Theorem 2 and Theorem 3.
3.2 Based on ideal two-level correlation binary sequence pair
Theorem 5Give an ideal two-level correlation binary sequence pair(s,s′)whose length is an odd number q and the in-phase correlation value is F.The weight of s is(q+1)/2.The line sequences xj(t)ofAand yj(t)ofBare defined as
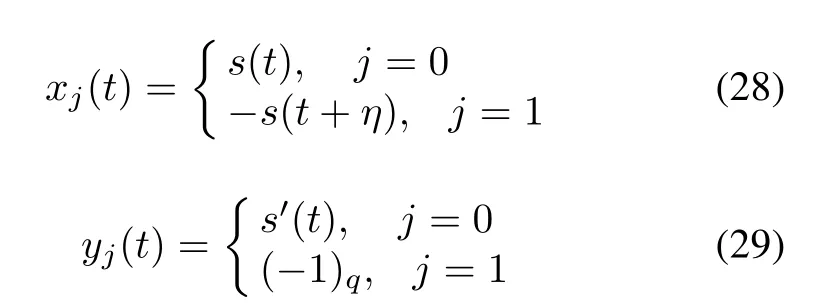
for 0≤t≤q-1,where j=0,1 and 0≤η≤q-1 is any fixed integer. By Construction 1, the obtained sequence pair(u,v)is an almost perfect binary sequence pair and the correlation value is presented as
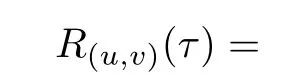
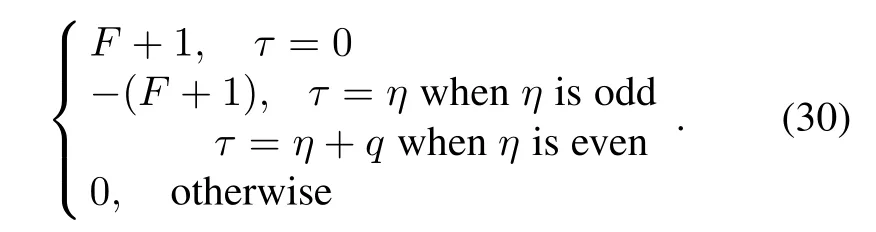
ProofSimilar to Theorem 1,we compute the values of R(u,v)(τ)as the following two cases.
(i)For τ1=0 and τ2≡ 0(modq),it is clear that
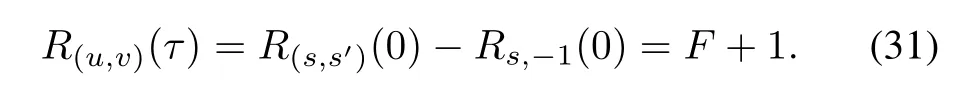
(ii)For τ1=1,R(u,v)(τ)is calculated as
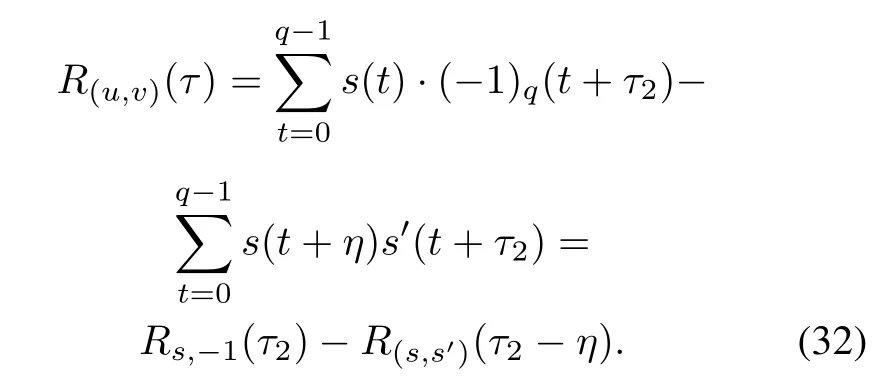
When τ2- η≡ 0(modq),we get τ= η for η is an odd integer and τ= η +q for η is an even integer.In this case,(32)is rewritten as
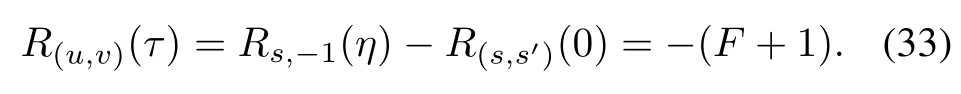
When τ2- η /=0(modq),(32)is represented as
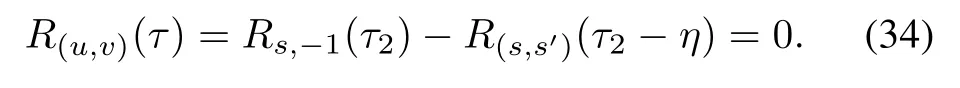
Corollary1Give two Legendre sequences g and g′defined as before whose length are q≡1(mod4).The line sequences xj(t)and yj(t)are defined as

for 0≤t≤q-1,where j=0,1 and 0≤η≤q-1 is any fixed integer. By Construction 1, the obtained sequence pair(u,v)is an almost perfect binary sequence pair with the correlation values presenting as
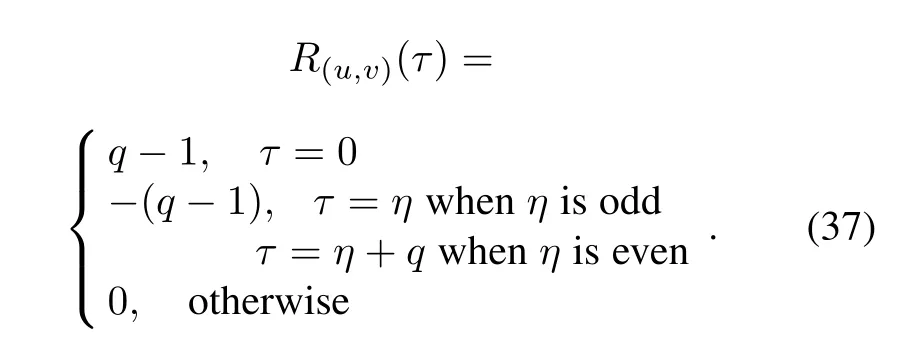
ProofBy the cross-correlation property of Legendre sequences described in Lemma 3 and similar to Theorem 5,the constructed sequence pair is an almost perfect binary sequence pair. □
Many types of ideal two-level correlation binary sequence pairs used in Theorem 5 can be found in[11],so many different types of almost perfect binary sequence pairs and DDSP can be obtained in our paper.However,the detailed parameters of DDSP are determined by the used binary sequence pair.Similar to Theorem 2,the DDSP(D,D′)based on Theorem 5 is presented as follows.
Theorem 6Give two characteristic sets U and V of the sequences s and s′respectively.Let the sets D and D′be the characteristic sets of the constructed sequences u and v in Theorem 5 respectively.Apparently,
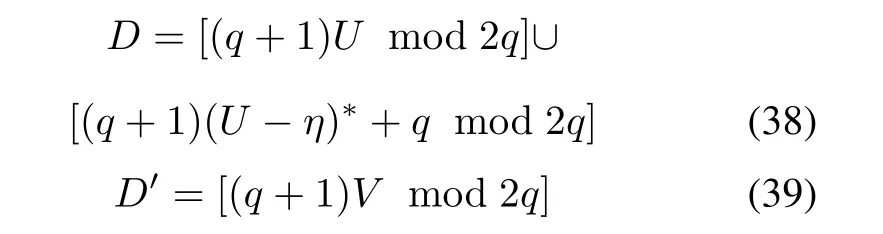
where(U- η)?represents the complement of(U- η)in Zq.In addition,

where ψ(t)=(t mod 2,t mod q)is the isomorphism from Z2qto Z2×Zq.
ProofThe proof is deleted as similar to Theorem 2.
Example 2Let g and g′be the two Legendre sequences of period 13 expressed as l=(1,1,-1,1,1,-1,-1,-1,-1,1,1,-1,1)and l′=(-1,1,-1,1,1,1-1,-1,-1,-1,1,1,-1,1)and let η=2.By Corollary 1,an almost perfect binary sequence pair(u,v)with length 26 is constructed as
And the correlation values R(u,v)(τ)for 0≤ τ≤ 25 are expressed as

By Theorem 6, the characteristic sets(D,D′)of the almost perfect binary sequence pair(u,v)derived in Theorem5 is listed as
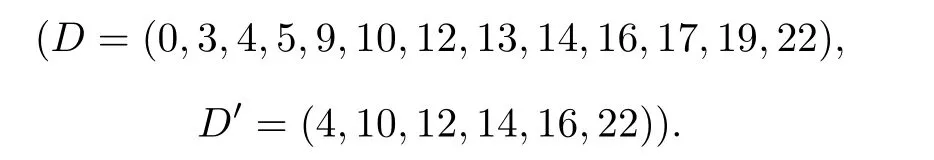
Similar to Example 1,we can confirm(D,D′)is a DDSP with parameters of(26/2,2,13,6,0,3).
4.Conclusions
In this work, two new methods by using Chinese remainder theorem for the almost perfect binary sequence pairs with period 2q are revealed,where q is an odd number.One method is from the binary ideal sequences and the other is from the ideal two-level correlation binary sequence pair.The obtained new signals can greatly extend the number of almost perfect sequences.In the engineering,any one of the two sequences can be used as the sending sequence.Assume that the number of“+1”element in any one of the binary sequence pair is p,which means that the almost perfect binary sequence pair(u,v)constructed in this paper has balance property.And we recommend using this sequence as the sending one.Furthermore,many new kinds of DDSPs can be got in this paper.
[1]JUNGNICKEL D,POTT A.Perfect and almost perfect sequences.IEEE Trans.on Information Theory,2001,47(6):2607–2608.
[2]TANG X H,GONG G.New constructions of binary sequences with optimal autocorrelation value/magnitude.IEEE Trans.on Information Theory,2010,56(3):1278–1286.
[3]BOZTAS S,PARAMPALLIU.Nonbinary sequences with perfect and nearly perfect autocorrelations.Proc.of the IEEE International Symposium on Information Theory Proceedings,2010:1300–1304.
[4]CHEN G,ZHAO Z Y.Almost perfect sequences based on cyclic difference sets.Journal of Systems Engineering and Electronics,2007,18(1):155–159.
[5]WOLFMANN J.Almost perfect autocorrelation sequences.IEEE Trans.on Information Theory,1992,38(4):1214–1418.
[6]POTT A,BRADLEY S P.Existence and nonexistence of almost-perfect autocorrelation sequences.IEEE Trans.on Information Theory,1995,41(1):301–304.
[7]WANG Y Z,XU C Q.Divisible difference set pair and approach for the study of almost perfect binary sequence pair.Acta Electronica Sinica,2009,37(4):692–695.(in Chinese)
[8]ZHAO XQ,HE W C,WANGZ W,et al.The theory of the perfect binary array pairs.Acta Electronica Sinica,1999,27(1):34–37.(in Chinese)
[9]JIN S Y,SONG H Y.Note on a pair of binary sequences with ideal two-level cross correlation.Proc.of the IEEE International Symposium on Information Theory,2008:2603–2607.
[10]JIN S Y,SONG H Y.Binary sequence pairs with two-level correlation and cyclic difference pairs.IEICE Trans.on Fundamentals of Electronics,Communications and Computer Science,2010,E93-A(11):2266–2271.
[11]PENG X P,XU C Q,ARASU K T.New families of binary sequence pairs with two-level and three-level correlation.IEEE Trans.on Information Theory,2012,58(11):6968–6978.
[12]PENG X P,XU C Q,LI G,et al.The constructions of almost binary sequence pairs and binary sequence pairs with three level autocorrelation.IEICE Trans.on Fundamentals of Electronics,Communications and Computer Science,2011,E94-A(9):1886–1891.
[13]SHEN X M,JIA Y G,SONG X F.Constructions of binary sequence pairs of period 3p with optimal three-level correlation.IEEE Communications Letters,2017,21(10):2150–2153.
[14]PENG X P,REN J D,XU C Q,et al.New families of binary sequence pairs with three-level correlation and odd composite length.IEICE Trans.on Fundamentals of Electronics,Communications and Computer Science,2016,E99-A(4):874–879.
[15]LIU X H,WANG J H,WU D H.Two new classes of binary sequence pairs with three-level cross-correlation.Advance in Mathematics of Communications,2015,9(1):117–128.
[16]TANG X H,GONG G.New constructions of binary sequences with optimal autocorrelation value/magnitude.IEEE Trans.on Information Theory,2010,6(3):1278–1286.
[17]DING C S,PEI D,SALOMAA A.Chinese remainder theorem:applications in computing,coding,cryptography.Signapore:World Scientific,1996.
 Journal of Systems Engineering and Electronics2018年2期
Journal of Systems Engineering and Electronics2018年2期
- Journal of Systems Engineering and Electronics的其它文章
- Health evaluation method for degrading systems subject to dependent competing risks
- Remaining useful life prediction for a nonlinear multi-degradation system with public noise
- Multi-focus image fusion based on block matching in 3D transform domain
- Hybrid artificial bee colony algorithm with variable neighborhood search and memory mechanism
- An optimization method:hummingbirds optimization algorithm
- Direction navigability analysis of geomagnetic field based on Gabor filter
