安徽省無為縣牛埠中學(xué)(238351) 朱小扣

圓錐曲線的考察一直是高考考察的重點,特別是對過焦點弦長問題的考察,但有時用常規(guī)的方法費(fèi)時費(fèi)力,筆者發(fā)現(xiàn)可以通過極坐標(biāo)方法可以秒殺此類問題.為此,先介紹如下兩個定理.

定理1已知橢圓的左右焦點分別為F1,F2.

(1)若以左焦點F1為極點,射線F1x為極軸建立極坐標(biāo)系,則橢圓C的極坐標(biāo)方程是:其中P 是左焦點到左準(zhǔn)線的距離,e為離心率.

(2)若以右焦點F2為極點,射線F2x為極軸建立極坐標(biāo)系,則橢圓C的極坐標(biāo)方程是:,其中P 是右焦點到右準(zhǔn)線的距離,e為離心率.

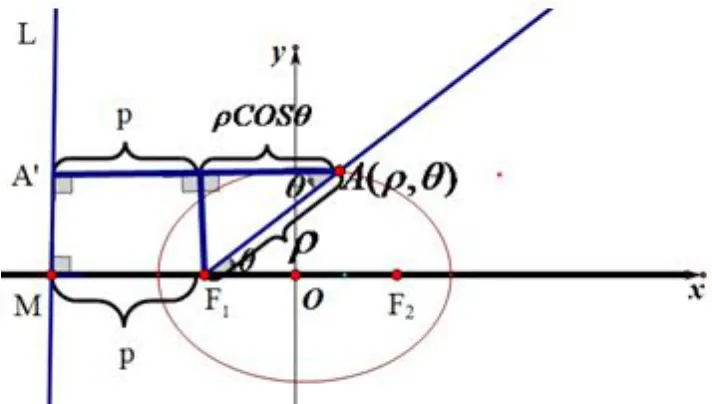
圖1

證明(1)設(shè)A(ρ,θ)是橢圓C上任意一點,如圖1可得,,由橢圓的第二定義得:,即所以所以橢圓C的極坐標(biāo)方程是:同理可證(2)此時橢圓C的極坐標(biāo)方程是:

定理2若曲線C為橢圓,其左右焦點分別為F1,F2.過F1的直線l交橢圓C于A,B兩點,以左焦點F1為極點,射線F1x為極軸建立極坐標(biāo)系,若A(ρ1,θ),B(ρ2,π + θ),則 |AB|= ρ1+ ρ2.若以右焦點建立極坐標(biāo)系,亦然.若曲線C是拋物線,|AB|=ρ1+ρ2,但若曲線C是雙曲線,|AB|=|ρ1+ρ2|.

1.1定理1的直接運(yùn)用

例1過左焦點F1且傾斜角為60°的直線與橢圓交與A,B兩點,若,則橢圓的離心率等于___.

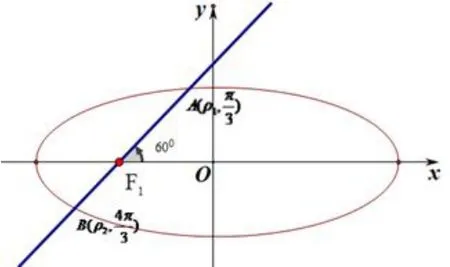
圖2

解 如圖2,以左焦點F1為極點,射線F1x為極軸建立極坐標(biāo)系,設(shè).由知,即

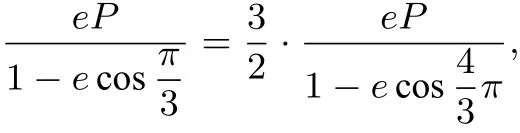
上述例題的解法,方法過程都很簡單,適合學(xué)生的一種新的解法,在高考和競賽中,像例一這類題變式很多,基本上都可以用極坐標(biāo)的方法解決,如例2.

例2(2016年遼寧省預(yù)賽)已知點F為橢圓1(a＞b＞0)的右焦點,橢圓的離心率為,過點F的直線l交橢圓于A,B兩點(點A在x軸的上方),且則直線l的斜率為___.

解由定理一,極點在右焦點的橢圓極坐標(biāo)方程為設(shè) A(ρ1,θ),B(ρ2,π+θ). 由知ρ1=3ρ2,即所以,所以,即斜率為

1.2 定理1的變式運(yùn)用

例3(2011年浙江理科)設(shè)F1,F2分別是橢圓1的左右兩個焦點,點A,B在橢圓上,若,則點A的坐標(biāo)是___.

解設(shè)B關(guān)于原點O的對稱點為B′,由橢圓的對稱性得到,以左焦點F1為極點,射線F1x為極軸建立極坐標(biāo)系,設(shè)A(ρ1,θ),B′(ρ2,θ+π). 由ρ1-=5ρ2知,所以,所以,易得 A(0,±1).

2.1 定理2的直接運(yùn)用

例4過雙曲線的右焦點,引傾斜角為的直線,交雙曲線與A,B兩點,求|AB|.

2.2定理2的變式運(yùn)用

例5(2017年課標(biāo)I卷理科)已知F為拋物線C:y2=4x的焦點,過F作兩條互相垂直的直線l1,l2,直線l1與C交于A,B兩點,直線l2與C交于D,E兩點,則|AB|+|DE|的最小值)

A.16 B.14 C.12 D.10

解如圖3,以左焦點F為極點,射線Fx為極軸建立極坐標(biāo)系,設(shè) A(ρ1,θ),

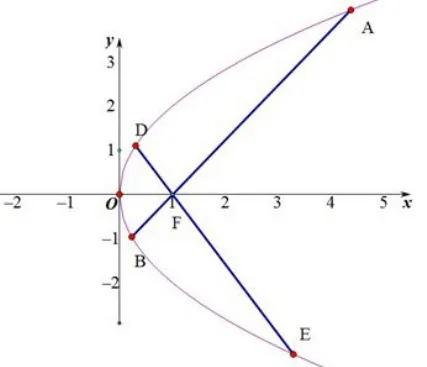
圖3

由定理2可得:

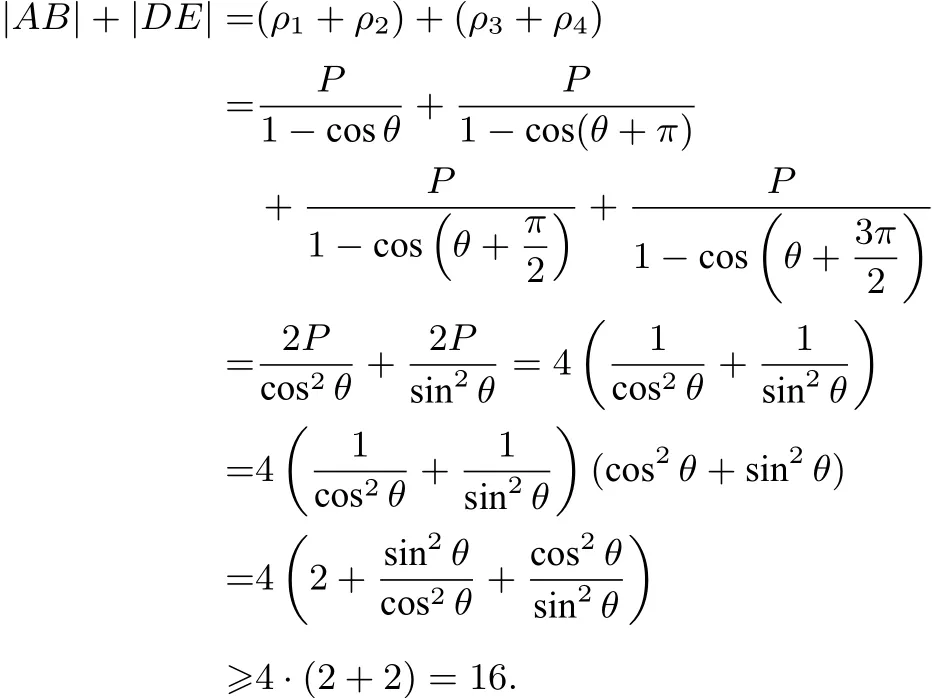
3.定理1,定理2的綜合運(yùn)用

圖4

(1)橢圓C的離心率e;

解(1)如圖4,以右焦點F為極點,射線Fx為極軸建立極坐標(biāo)系,設(shè),由知ρ1=2ρ2,即

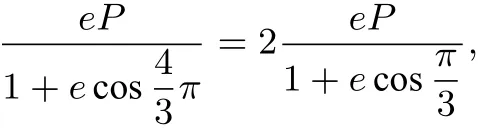
(2)由(1)得:

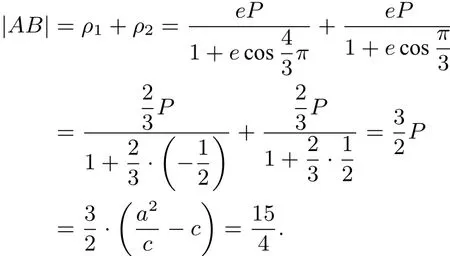
點評用極坐標(biāo)這種方法有時相比標(biāo)準(zhǔn)答案提供的解法,不僅省時省力,而且,準(zhǔn)確率高,而很多學(xué)生和教師經(jīng)常會忽略這種解法,所以本文希望能給這些同學(xué)有所啟發(fā),學(xué)會試著用極坐標(biāo)的方法解題.

總結(jié)用極坐標(biāo)的方法不僅可以解決橢圓中的問題,也可以解決雙曲線,拋物線的問題,不能認(rèn)為極坐標(biāo)僅僅應(yīng)用在高考的選做題上,實際上,極坐標(biāo)的作用非常巨大,可以秒殺過圓錐曲線焦點弦的問題.同時,教師在上課時也要注重培養(yǎng)學(xué)生一題多解的能力,這樣才能更好的掌握數(shù)學(xué)知識與方法,也能使學(xué)生數(shù)學(xué)成績達(dá)到質(zhì)的提升.