Diana De Padova, Michele Mossa,Stefano Sibilla

?

SPH numerical investigation of the characteristics of an oscillating hydraulic jump at an abrupt drop*

Diana De Padova1, Michele Mossa1,Stefano Sibilla2

1.2.

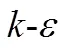
Hydraulic jumps, smoothed particle hydrodynamics (SPH) models, oscillating characteristics

Introduction

At an abrupt drop the transition from supercri- tical to subcritical flow is characterised by several flow patterns depending upon the inflow and tailwater flow conditions. Figure 1 summarises well acknow- ledged flow patterns.

Some researchers pointed out the existence of oscillating phenomena[2-5]. These oscillating character- istics can consist of: (1) change from one type of hydraulic jump to another, (2) horizontal movement of the jump toe, (3) cyclic variation of velocity compo- nents and pressure in the region close to the jump roller, (4) formation, development and coalescence of large-scale flow structures.

As shown by Ref. [6], specific flow conditions can lead to cyclic oscillations between jump types, resulting in the cyclic formation and evolution of jump vortices.

MeshlessLagrangiantechniquesappearto be par- ticularly suitable to represent the complexandhighly- unsteady free-surface patterns which characterize a hydraulic jump: a number of realizations obtained with smoothed particle hydrodynamics (SPH) have shown that this method can be successfully applied to the simulation of standing waves[7-9], of wave trains issuing from flapping jets[10], of hydraulic jumps[11-14]and of spilling breakers[15], being able to reproduce, both qualitatively and quantitatively, their average and time-dependent features.

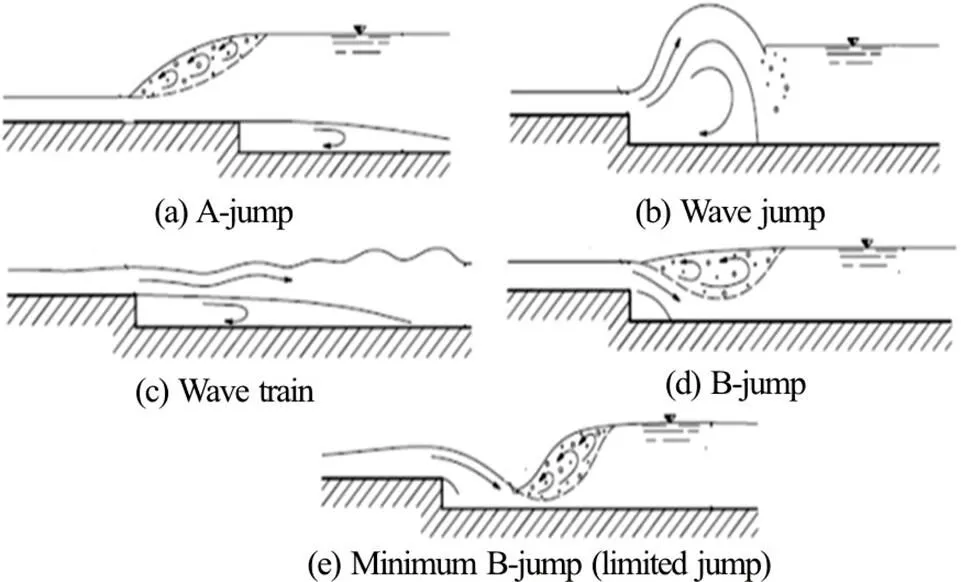
Fig.1Flow conditions (from Ohtsu and Yasuda[1])

The purpose of this paper is therefore to use a weakly-compressible SPH (WCSPH) scheme, toge- ther with a suitable turbulence model, to study the oscillating characteristics and cyclic mechanisms which can occur in a hydraulic jump at an abrupt drop in certain conditions, leading to an alternate shift of the flow pattern between the B-jump and the wave jump.

The numerical results are eventually compared to the laboratory experiments by Mossa et al.[6], in order to obtain a deeper understanding of the physical features of this particular kind of unsteady flow.

1. Experimental setup

Experimental investigations were carried out in the laboratory of the Civil and Environmental Eng- ineering Department-Water Engineering Division (hereafter referred to as SIA) of Bari Polytechnic University in a 0.4 m wide, 24.4 m long channel (with sidewalls 0.5 m height). The walls and bottoms of both channels were made of Plexiglas (Fig. 2). The channel hosted in recent years widespread experimen- tal activity on hydraulic jump characterization[4, 6, 16-19].

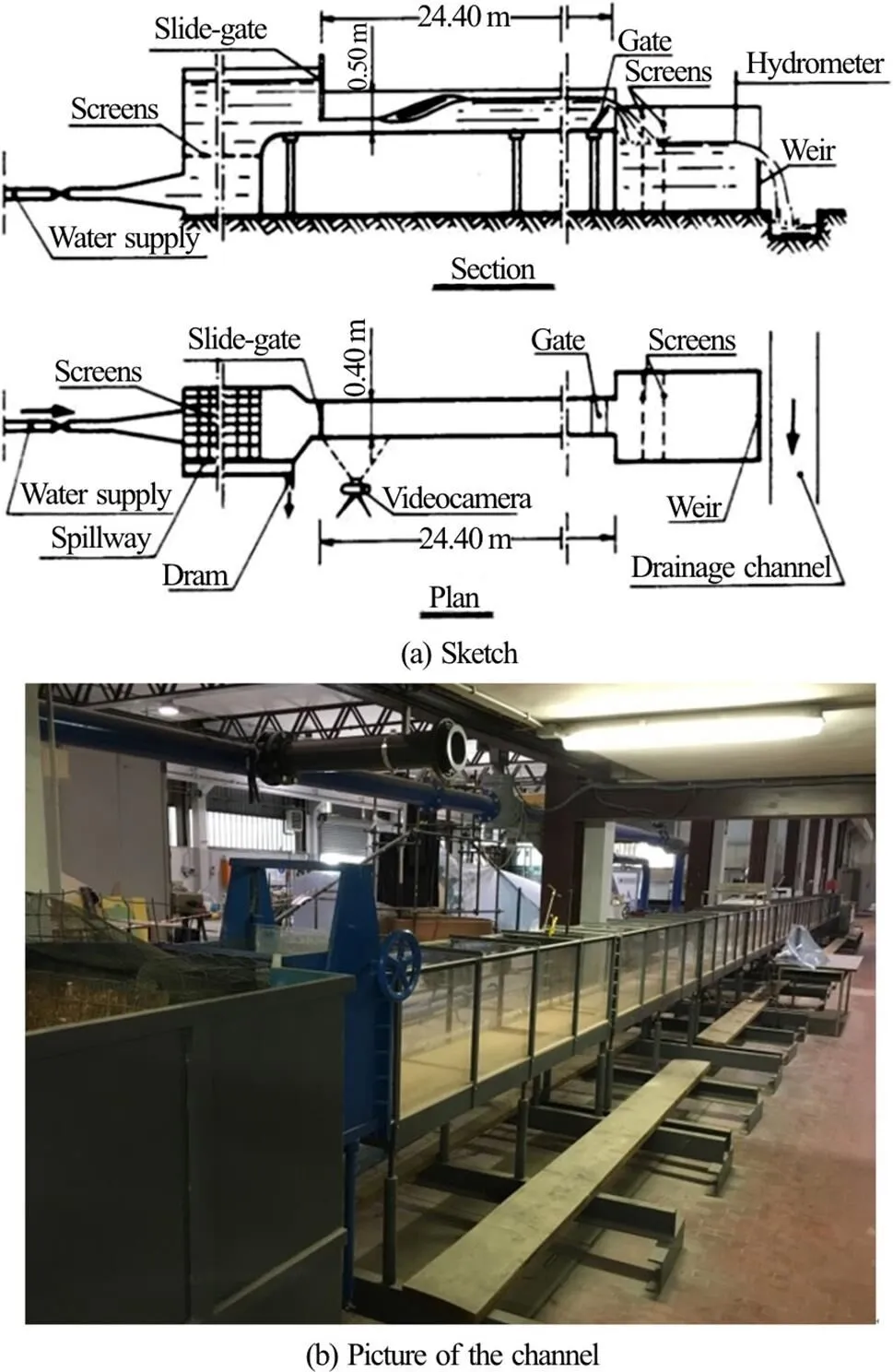
Fig.2(Color online) Channel at the hydraulic laboratory of the laboratory of the Civil and Environmental Engineering Department-Water Engineering Division of Bari Poly- technic University

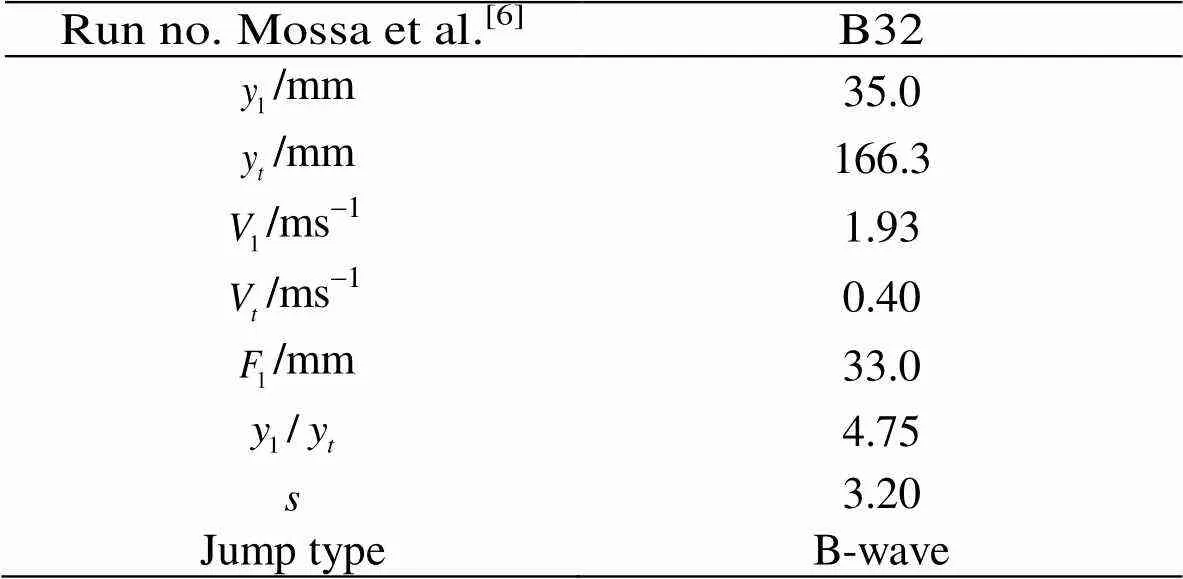
Table1Parameters of the analysed oscillating hydraulic jump

2. SPH numerical method

SPH simulations were obtained by a code developed at the Fluid Mechanics Laboratory of the Department of Civil Engineering and Architecture of the University of Pavia. The code solves the Navier- Stokes equations with a standard weakly compressible SPH (WCSPH) scheme[20, 21], where a reduced com- pressibility modulus of 106Pa is assumed for water and a pressure smoothing procedure is applied at every time step to the difference between local and hydrostatic pressure in order to reduce the numerical noise in pressure evaluation[11].

A renormalization procedure for the SPH kernel approximation is applied to enforce consistency on the numerical estimate of the derivatives in the velocity and stress divergence terms[22].

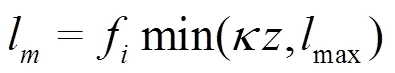
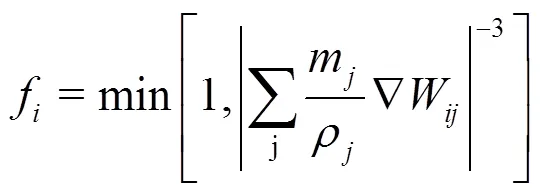
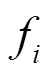
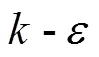
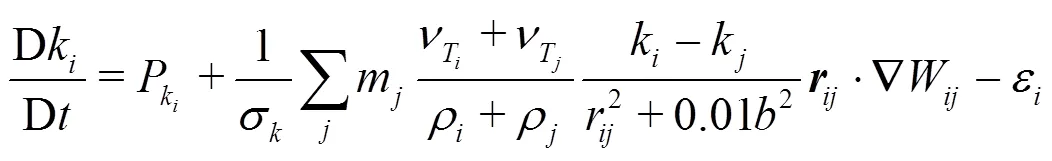
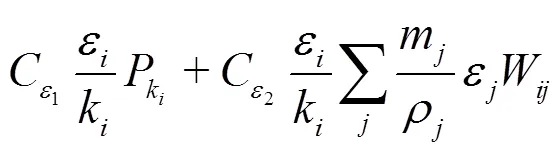
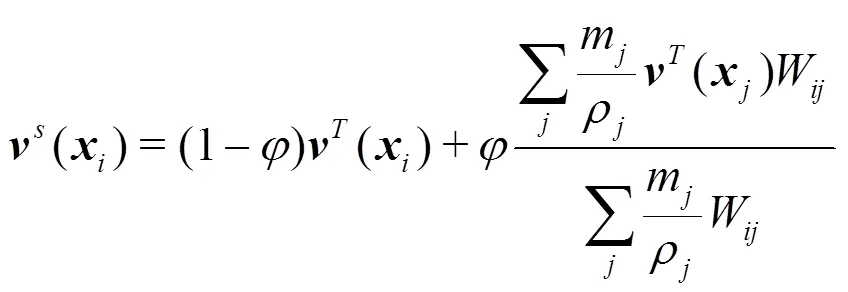
and used for particle movement. The smoothing para- metercontrols the intensity of velocity filtering.

3. Numerical test and results

The SPH 2-D simulation of the hydraulic jump reported in Table 1, wasperformed in a physical domain consisting in a rectangle 2.0 m long and 0.4 m high, shorter than the real channel in the test facility. The shorter domain was chosen in order to reduce the computational cost without influencing the quality of the numerical solution.

A schematic figure of the problem setup can be seen in Fig. 3.

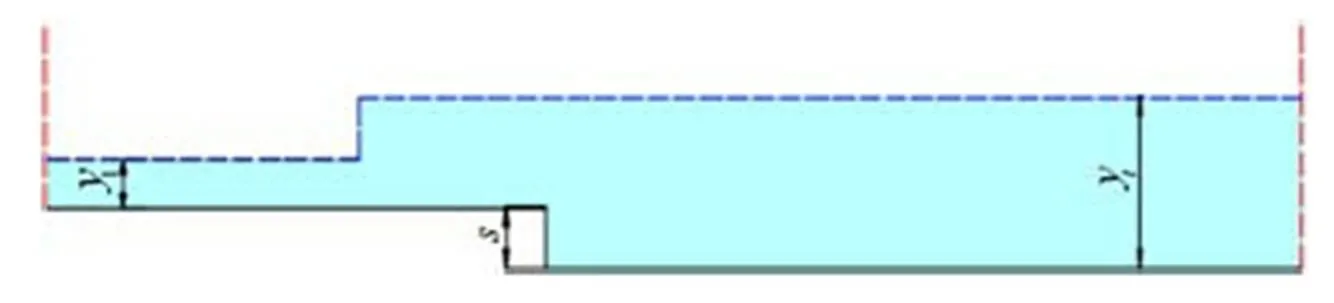
Fig.3(Color online) Schematic figure of the geometrical setup. Solid black lines indicates solid walls, dashed blue lines the initial free surface and dashed red lines show the position of the inflow and outflow boundaries

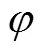
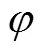
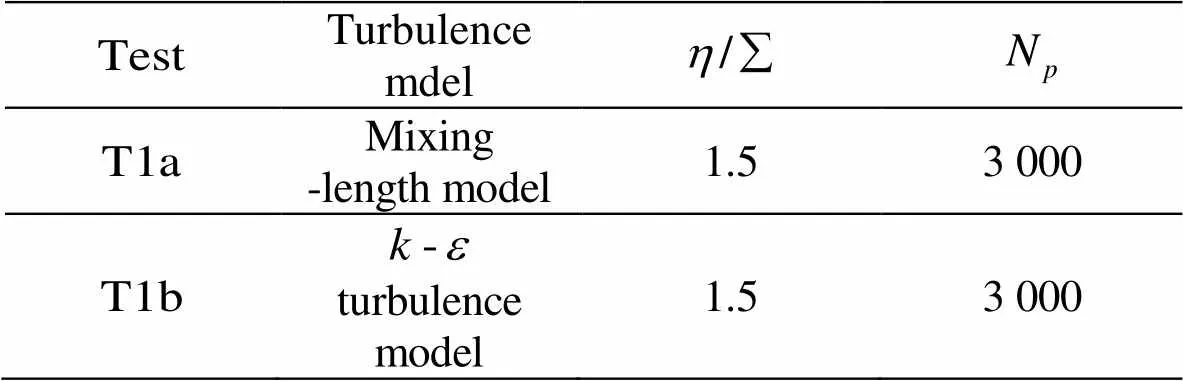
Table2Numerical parameters of the SPH simulations in the sensitivity analysis

The sensitivity analysis is here shown for test T1b, and shows that the vorticity field is predicted quite accurately even by the coarsest resolution, although some detail is lost in the middle of the roller (Figs. 6 and 8).

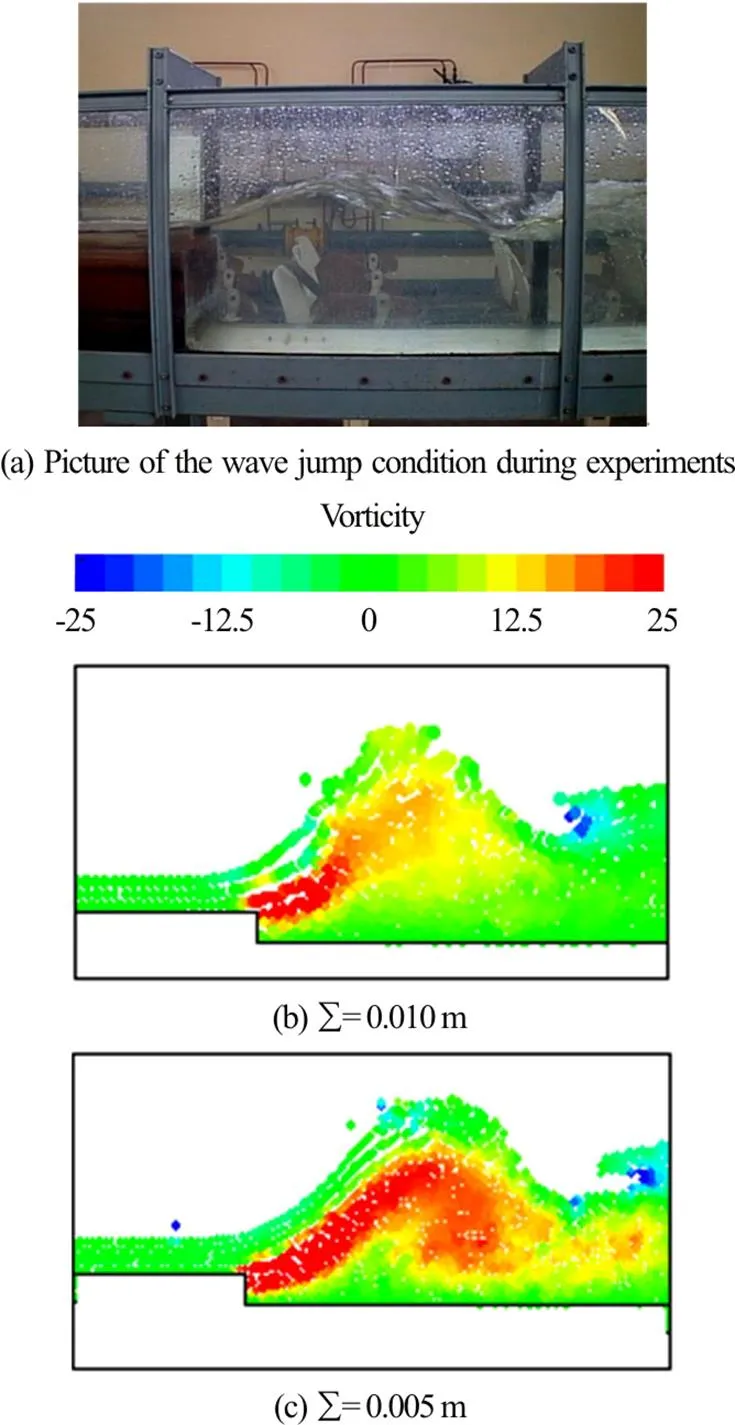
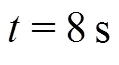
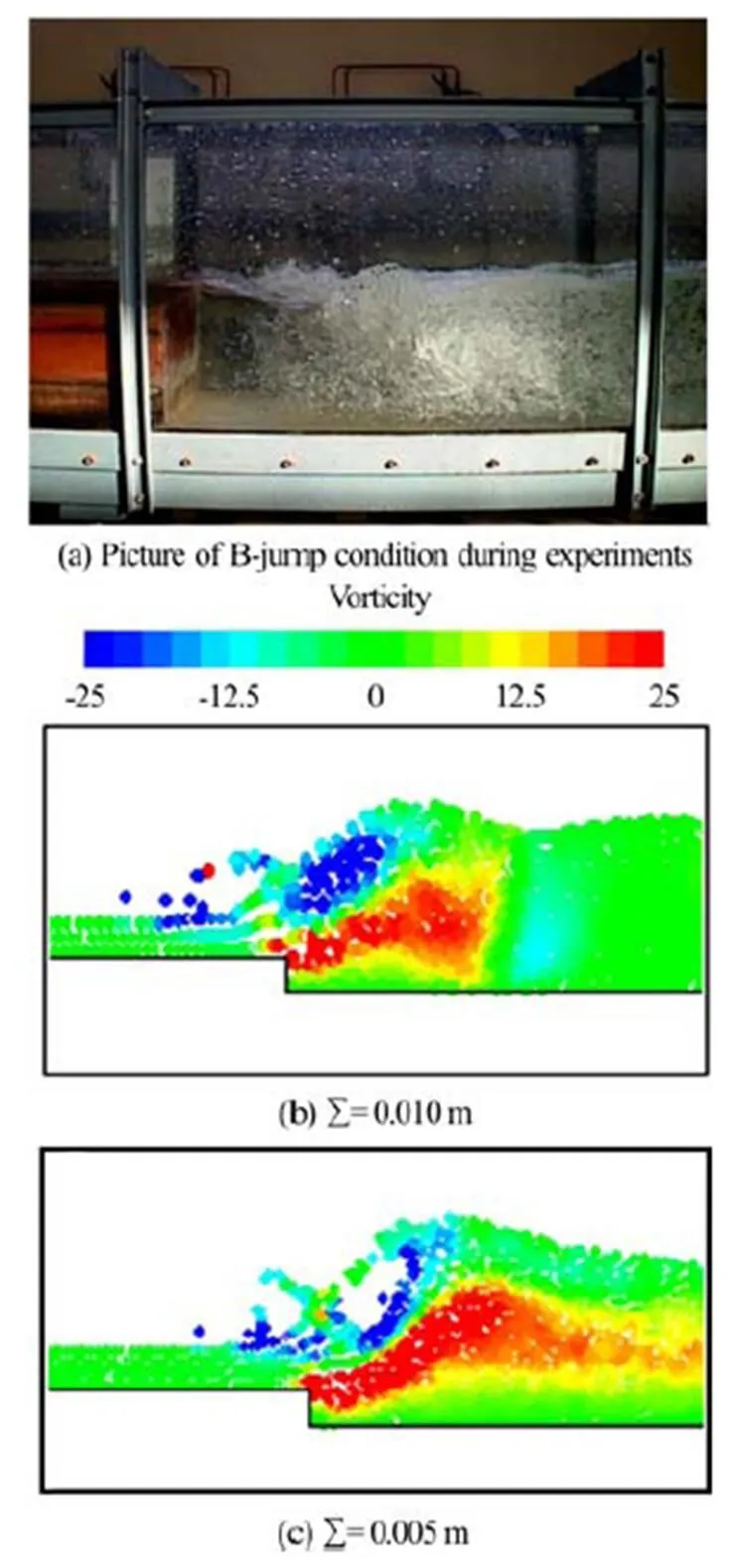
Fig.8 (Color online) Instantaneous SPH vorticity fields in the SPH simulation (Test T1b) with different particle resolutions. Color scale as in Fig. 4

Fig.9 (Color online) Instantaneous SPH turbulent kinetic energy fields (B-jump condition: ) in the SPH simulation (Test T1b) with different particle resolu- tions. Color scale as in Fig. 4

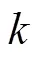
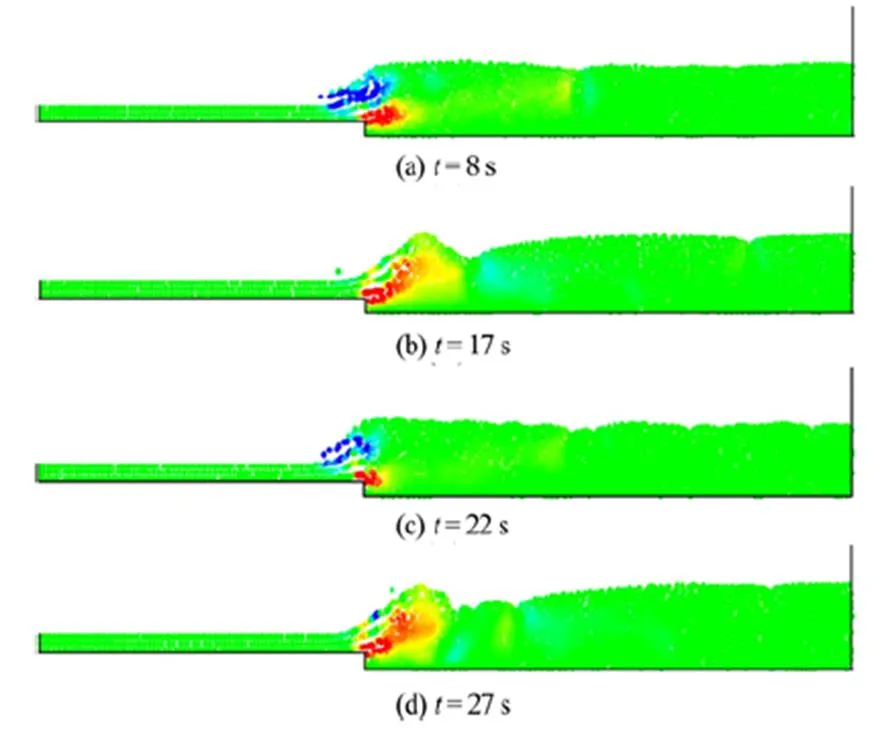
Fig.10 (Color online) Instantaneous SPH vorticity fields in the SPH simulation of Test T1a

Fig.11 (Color online) Instantaneous SPH vorticity fields in the SPH simulation of Test T1b

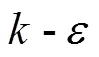
The instantaneous vorticity fields (Figs. 10(a)- 11(d)) of the configuration with oscillations between the B and wave jump clearly indicate that the transi- tion phase between the two jump types is well repro- duced by both turbulence models (T1a and T1b). Vortices are characterized by a clockwise or anti- clockwise rotation, depending on which type of jump is present. In particular, vortices are characterized by a clockwise rotation when the wave jump occurs (Figs. 10(b)-10(d) and Figs. 11(b)-11(d)) and by an anti- clockwise one for the B jump (Figs. 10(a)-10(c) and Figs. 11(a)- 11(c)), respectively.

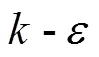
Figure 12 show the amplitude spectrum of the pressure fluctuations computed in tests T1a and T1b, compared with the measurements under the hydraulic jump B32 of Table 1, where the pressure tap was located at a distance of 0.26 m from the time-averaged position of the jump toe.

From the analysis of the spectrum it is clear that even the pressure fluctuations are quasi-periodic and strongly influenced by the oscillations between the B and wave jump types; furthermore, it is possible to observe the existence of a peak in each spectrum, as it was shown in the experiments by Mossa et al.[6].

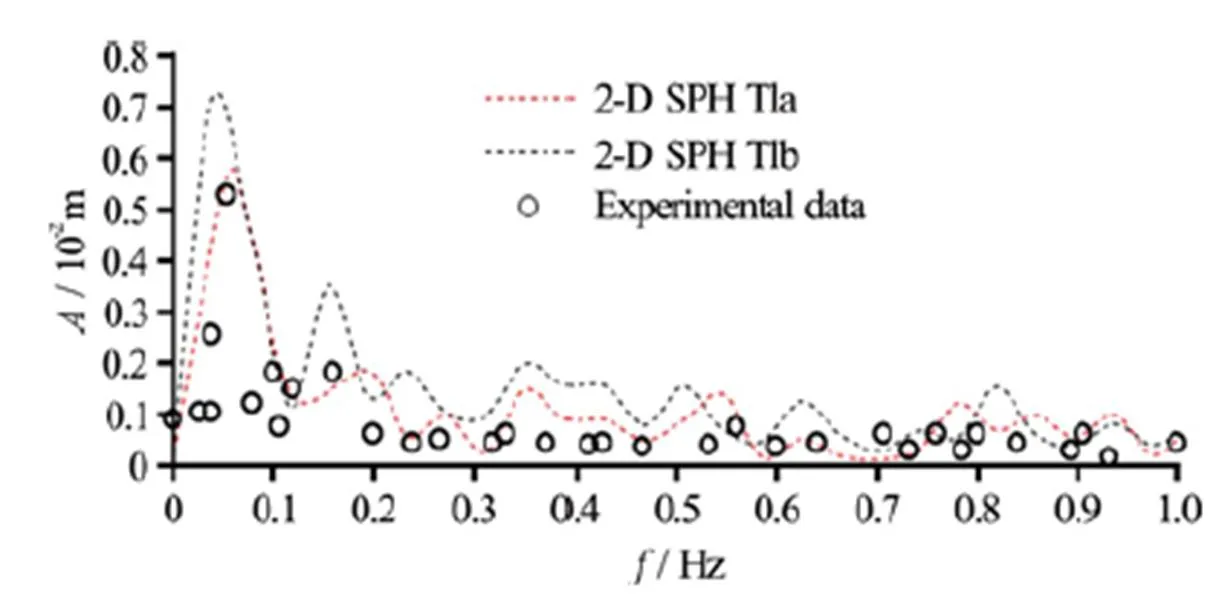
Fig.12 (Color online) Amplitude spectrum of pressure fluc- tuations under hydraulic jump (configuration B32 of Table 1) for the SPH simulations of test T1 and two different turbulence models: mixing-length (T1a) and (T1b)

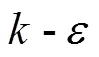
From the analysis of the Figs. 13(a)-13(c), it is clear that velocity components and pressure fluctua- tions, are strongly influenced by the oscillations between the B and wave jump types. The time histories (Fig. 13(a)) show that low pressures (low water depths) can be correlated with the horizontal flow upstream of the wave-jump, while higher pressures (and depths) can be correlated with the upward flow caused by the roller in the B-jump phase. Therefore, the analysis of the oscillating phenomena indicates a correlation among the velocity components and pressure fluctuations.

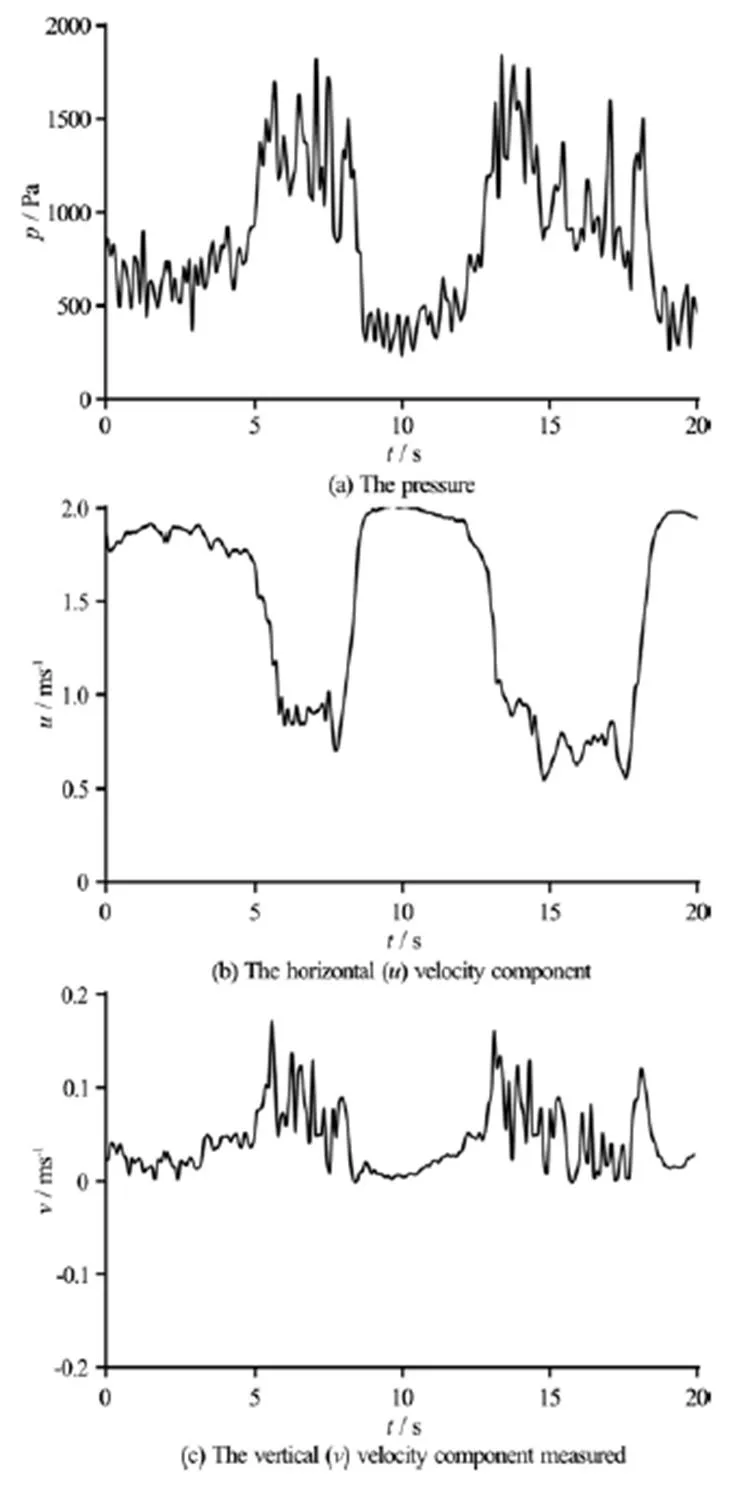
Fig.13 Time series at the bottom under the hydraulic jump

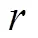
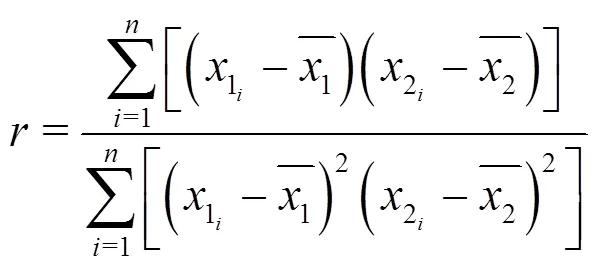
This result is consistent with the oscillation between the B-jump (Figs. 11(a) and 11(c)) and the wave-jump (Figs. 11(b) and 11(d)) patterns.

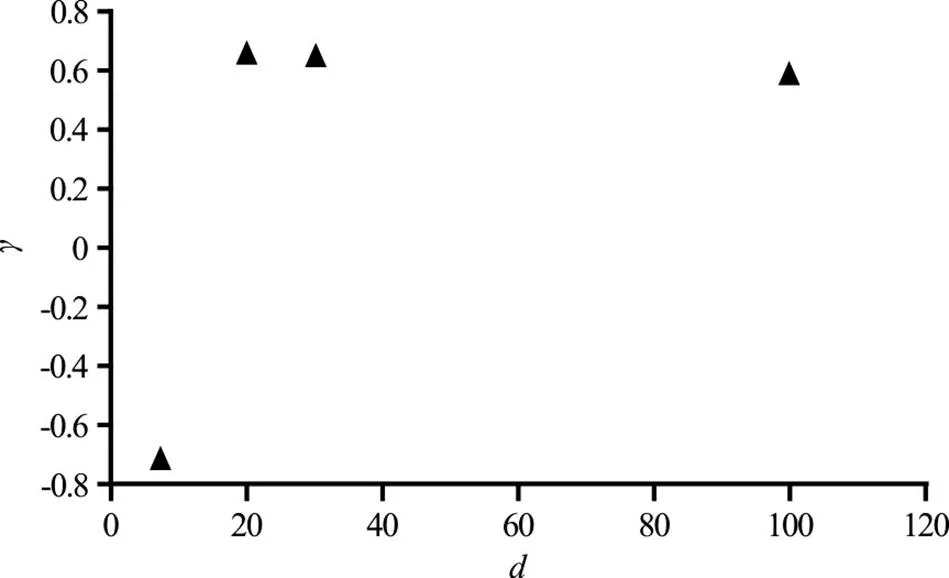
Fig.14Correlation coefficients between pressure and stream- wise velocity component as a function of the distance d from the average toe position

4. Conclusions

As observed experimentally by Mossa et al.[6], these numerical results show the existence of a peak at a similar frequency in the amplitude spectra of the time series of the surface elevations upstream and downstream of the jump, in the amplitude spectra of the pressure and in the amplitude spectra of the velocity components fluctuations measured under the hydraulic jump.

It is possible to conclude that the SPH numerical simulations yield results which are in qualitative and quantitative agreement with the experiments: hence SPH can be used as a reliable “numerical experiment” which allows one to get a better insight in the unsteady flow phenomenon, performing detailed eva- luations which can be complicated to be obtained during laboratory experiments. For instance, the analysis of amplitude spectra, of the vorticity fields and of the correlation coefficients indicates that velocity components and pressure fluctuations, are strongly influenced by the oscillations between the B and wave jump types, and that a strong correlation exists among the velocity and vorticity fields and the pressure fluctuations even far downstream of the jump position.

[1] Pagliara S. Transition from supercritical to subcritical flow at an abrupt drop [J]., 1992, 30(3): 428-432.

[2] Nebbia G. Su taluni fenomeni alternativi in correnti libere [J], 1942, XIX(1): 1-10.

[3] Abdel Ghafar A., Mossa M., Petrillo A. Scour from flow downstream of a sluice gate after a horizontal apron [C]., New Delhi, India, 1995, 1069-1088.

[4] Mossa M. On the oscillating characteristics of hydraulic jumps [J]., 1999, 37(4): 541-558.

[5] Wang H., Chanson H. Experimental study of turbulent fluctuations in hydraulic jumps [J]., 2015, 141(7): 04015010.

[6] Mossa M., Petrillo A., Chanson H. Tailwater level effects on flow conditions at an abrupt drop [J]., 2003, 41(1): 39-51.

[7] Dalrymple R. A., Rogers B. D. Numerical modelling of waves with the SPH method [J]., 2006, 53(2-3): 131-147.

[8] Capone T., Panizzo A., Monaghan J. J. SPH modelling of water waves generated by submarine landslides [J]., 2010, 48(Suppl. 1): 80-84.

[9] De Padova D., Dalrymple R. A., Mossa M. Analysis of the artificial viscosity in the smoothed particle hydrodynamics modelling of regular waves [J]., 2014, 52(6): 836-848.

[10]Espa P., Sibilla S., Gallati M. SPH simulations of a vertical 2-D liquid jet introduced from the bottom of a free-surface rectangular tank [J]., 2008, 3(2): 105-140.

[11]De Padova D., Mossa M., Sibilla S. et al. 3D SPH modelling of hydraulic jump in a very large channel [J]., 2013, 51(2): 158-173.

[12] Jonsson P., Andreassona P., Hellstr?m J. G. I. et al. Smoo- thed particle hydrodynamic simulation of hydraulic jump using periodic open boundaries [J]., 2016, 40(19-20): 8391-8405.

[13] De Padova D., Mossa M., Sibilla S. SPH modelling of hydraulic jump oscillations at an abrupt drop [J]., 2017, 90: 790-814.

[14]De Padova D., Mossa M., Sibilla S. SPH numerical investigation of characteristics of hydraulic jumps [J]., 2017,

https://doi.org/10.1007/s10652-017-9566-4.

[15]De Padova D., Mossa M., Sibilla S. SPH numerical inves- tigation of the velocity field and vorticity generation within a hydrofoil-induced spilling breaker [J]., 2016, 16(1): 267-287.

[16]Mossa M., Tolve U. Flow visualization in bubbly two- phase hydraulic jump [J]., 1998, 120(1): 160-165.

[17]Mossa M. Discussion on “Relation of surface roller eddy formation and surface fluctuation in hydraulic jumps” by K. M. Mok [J]., 2005, 43(5): 588-592.

[18]Mossa M., Petrillo A., Chanson H. Discussion on the “Tailwater level effects on flow conditions at an abrupt drop” [J]., 2004, 43(2): 217-224.

[19]Mossa M. Experimental study of the flow field with spilling type breaking [J]., 2008, 46(Suppl. 1): 81-86.

[20] Liu G. R., Liu M. B. Smoothed particle hydrodynamics: A meshfree particle methods [M]. Singapore: World Scienti- fic, 2005.

[21] Monaghan J. J. Simulating free surface flows with SPH [J]., 1992, 110(2): 399-406.

[22]Sibilla S. An algorithm to improve consistency in smoo- thed particle hydrodynamics [J]., 2015, 118: 148-158.

[23]De Padova D., Mossa M., Sibilla S. Laboratory experi- ments and SPH modelling of hydraulic jumps [C]., Nantes, France, 2009, 255-257.

[24]De Padova D., Mossa M., Sibilla S. et al. Hydraulic jump simulation by SPH [C]., Manchester, UK, 2010, 50-55.

[25] Launder B. E., Spalding D. B. The numerical computation of turbulent flows [J]., 1974, 3(2): 269-289.

[26] Dehnen W., Aly H. Improving convergence in smoothed particle hydrodynamics simulations without pairing instability [J]., 2012, 425(2): 1068-1082.

[27] De Padova D., Dalrymple R. A., Mossa M. et al. An an- alysis of SPH smoothing function modelling a regular breaking wave [C]., Perugia, Italy, 2008.

(October 31, 2017, Accepted December 14, 2017)

?China Ship Scientific Research Center 2018

Diana De Padova (1981-), Female, Ph. D.,

Research Assistant

Diana De Padova,

E-mail:diana.depadova@poliba.it