Wei Wang·Yongzhi Zhang·Jun Cao·Wenlong Song

Introduction

With the implementation of state-owned forest reform,all the key state-owned forest areas in Heilongjiang province are closed to commercial harvesting,so forest enterprises must use available resources.The utilizable forest resource in production is limited.The natural growth of the raw material,timber logs,varies considerably over long growth periods.As the demand for wood products increases,timber mills must improve the utilization of logs to meet market needs and develop their business.

Traditional timber processing is not flexible enough,and there is no way to measure and control the variations in the volume of timber in timber processing.This problem lowers the value and volume of lumber output and increases the cost of manufacturing.A robust optimization approach is able to control the effect of variations in volume of timber available,and offers a scienti fic theory for timber processing.

The robust optimization approach was first applied by Soyster(1973).Further research has been conducted on robust optimization using different approaches(Bertsimas and Sim 2004a,b;Leung and Chan 2009).This methodology has been applied successfully to different types of problems and to uncertainties in forest production(Zanjani et al.2010;Alvarez and Vera 2014;Varas et al.2014;Alem and Morabito 2012).

Based on the robust optimization theory,this thesis make a research of production plan and make an optimization for traditional timber processing.The research technical route shown as Fig.1:

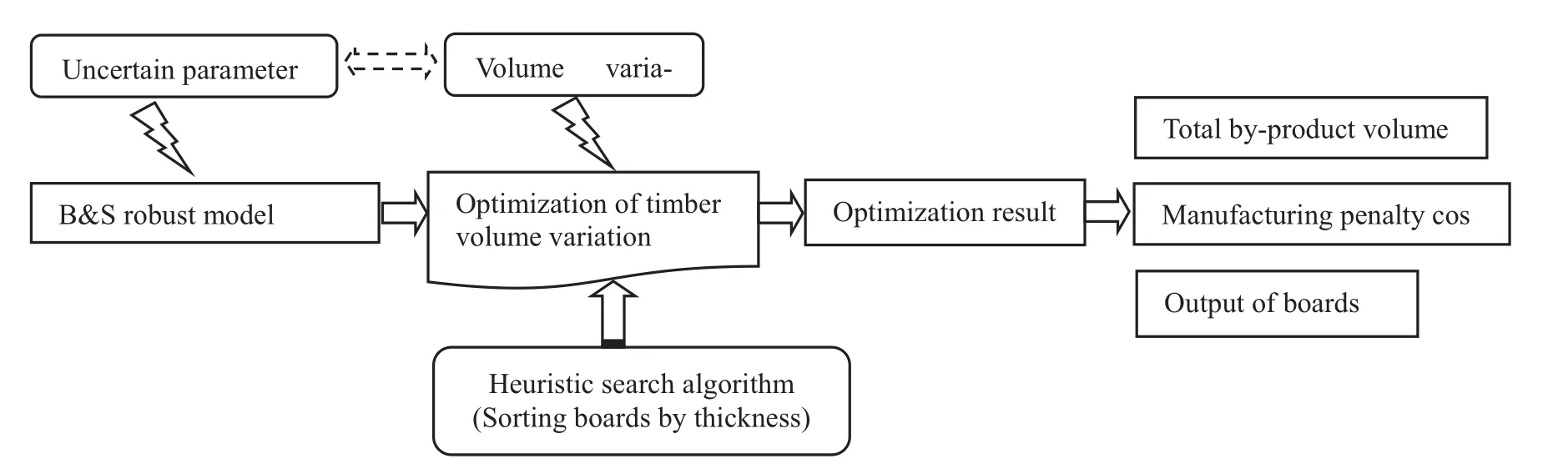
Fig.1 Research technical route

Materials and methods

Robust optimization and B&S(Bertsimas and Sim)robust model

Robust optimization is a modeling method of manipulating data uncertain(Bental et al.1999;Ben-Tal and Nemirovski 2000).The purpose of robust optimization is to ful fill the model constraints and to control the data simultaneously.Using robust optimization,the original model related to an uncertainty problem is changed to a semi-in finite robust optimization model using a corresponding formula.The feasible solution and the optimum solution are de fined as the robust feasible solution and the robust-optimum solution of the uncertainty problem.The quantitative repeatability of robustness:

where,Φ is the assemblage of all performance characteristics, φithe i parameter in assemblage Φ, πjthe j parameter that effects disturbance of object function,μ the robust mapping,rμ（φi,πj）the robust radius of mapping μ,when taking φiand πjinto account,and ρμ（Φ,πj）is the robust of mapping μ when taking Φ and πjinto account.

The B&S robust model advanced by Bertsimas and Sim(Bertsimas and Sim 2003,2004a,b),comes from linear programming.The assemblage,which is formed from the columns of uncertain parameter aijin i line of coef ficient matrix A,is de fined as the assemblage Ji;aijcan be regarded as a symmetrically and limited random variablethe de finition domain isto every bound i,using parameterto adjust conservative level of solutions.In the B&S robust model,the minimum whole number is no greater than the uncertain date aijis changing in intervalcoef ficient is changing inThe corresponding formula of robust is:

Construction of the volume variation robust optimization model

Description of problems

If the quantity of boards in an order is n(use i=1,…,n),the thickness of the boards is ui;the width of boards is wi;then every board must be produced from standard diameter logs on a band saw.Traditional timber processing would use the principle of manufacturing first and then cleaning up.Standard logs k would be produced by a standard cutting scheme e0.Defective boards would be discarded after timber processing.Boards produced from the same log are kept to the same thickness to reduce the time needed for band saw adjustment.An adjustment penalty cost is assessed if the thickness must be changed and given the valuethe penalty parameter is γu.The board thickness should meet the width limit for the boards produced.If the width is more than or less than the width limit,there will be a penalty costthe penalty parameters areIf the total volume of lumber is less than volume of logs,there will be a volume penalty costthe penalty parameter is γvt.

Since the band saw only works on one log at any moment,and the production process is continuous without interruption,the minimum coef ficient of utilization in timber processing isThe timber mill manufactures boards based on clients’orders with the goal of maximizing output with minimum logs and penalty cost.

Robust optimization model

When defective logs comes out in timber processing,they must be discarded.Based on the need to maximize board output per log,the timber mill sorts raw material logs into groups for processing,which changes the volume.In this paper,we use B&S robust model to control the volume variation of timber in processing.The meanings of the symbols in this model are as follow:

Combine object function and linear form of robust formula,so the robust optimization model is:

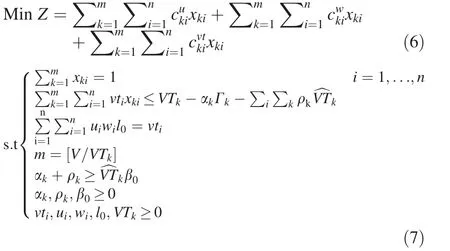
Algorithm for solution

For the volume variation robust optimization model in timber processing,based on the strategy of sorting boards into groups by thickness which is written by Zanjani(2010),using the highly ef ficient search algorithm where data is limited(Liu and Lin 2005).Solving involves trying to figure out the best mapping relationship between boards and logs.Algorithm design was as follows(Varas et al.2014;Maturana et al.2009):

Step 1 Order and number the slabs according to thickness ui,mark them withtotal get I groups,Step 2 Calculate minimum volume of logs mMinand maximum volume of logs mMax,sending each group raw material logs lj;and record the mapping between slabs and logs using 0–1 matrix Nki;calculate probability matrix Pkiproducing boards from logs by matrix Nki,and

Step 3 Get original solution matrixby comparing with random number sequence and probability matrix;Step 4 Estimate the relationship between volume of slabs and available volume of logs.Calculate object function valueand slabs penalty costof.Replace the maximum penalty cost of slabs with the minimum penalty cost of slabs.Estimate the relationship between the volume of slabs and logs and calculate object function value

Step 5 Estimate the relationship betweenuntil iteration finished and get the best solution

Optimization of timber volume variation

Manufacture data

In this paper,using small diameter oak with a diameter of 20 cm,and length of 2 m as the raw material.Based on the purchase order,there are 57 boards to produce,divided into different groups by thickness.The requirements for different size slabs is in Table 1.

According to the parameters in robust optimization model,take γu=δk=0.50,VTk=0.0720.The maximum unit of thickness penalty is 5 mm,and the minimum unit of thickness penalty is 2 mm.

Evaluating indicator

For the volume variation of the robust optimization model in this paper,we evaluated timber processing with the sawn timber volume per log,the by-product volume per log and the total output of boards.We compared and analyzed traditional timber-processing models and the robust optimization model to get a result by using an evaluation indicator.

The sawn timber volume of per log(%):

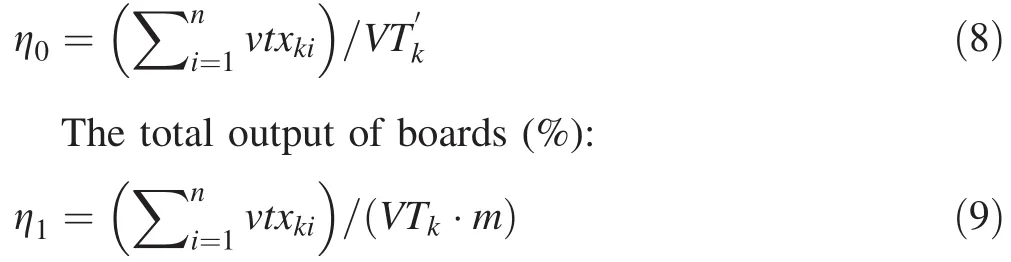
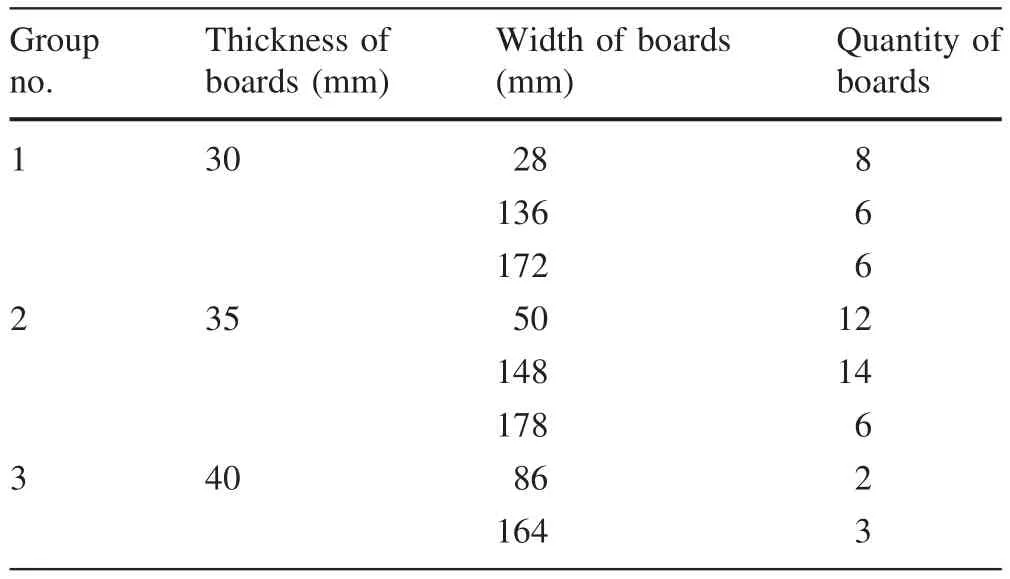
Table 1 Requirements for different size slabs

The by-product volume of per log(%):

Results

We used MATLAB to seek a solution to the robust-optimization model with controllable variation in the volume of timber.In order to quantify cutting pattern changes in the robust optimization model when it was controlling volume variation of timber,we chose No.2 log with defective quality for comparison and analysis.The result is expressed in Tables 2 and 3.The defects in these tables were cutting sawn timber defects,and the grade of boards was estimated by standard subdivision of boards.We compared indexes in timber processing processes according to different model results and optimize theeffects of the robust optimization model in controlling the variation problem of timber.Indexes of different models are shown in Table 4.

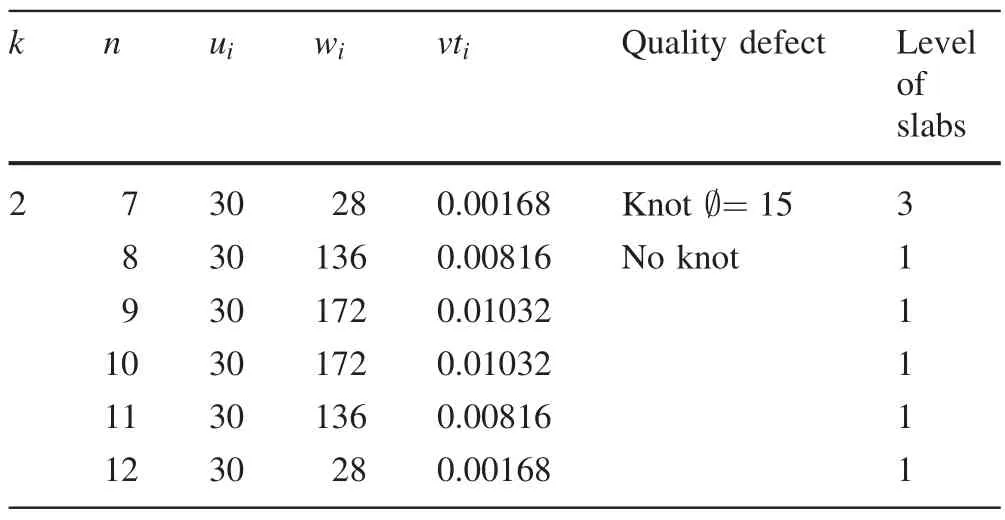
Table 2 Traditional timber processing model result

Table 3 Robust optimization model result

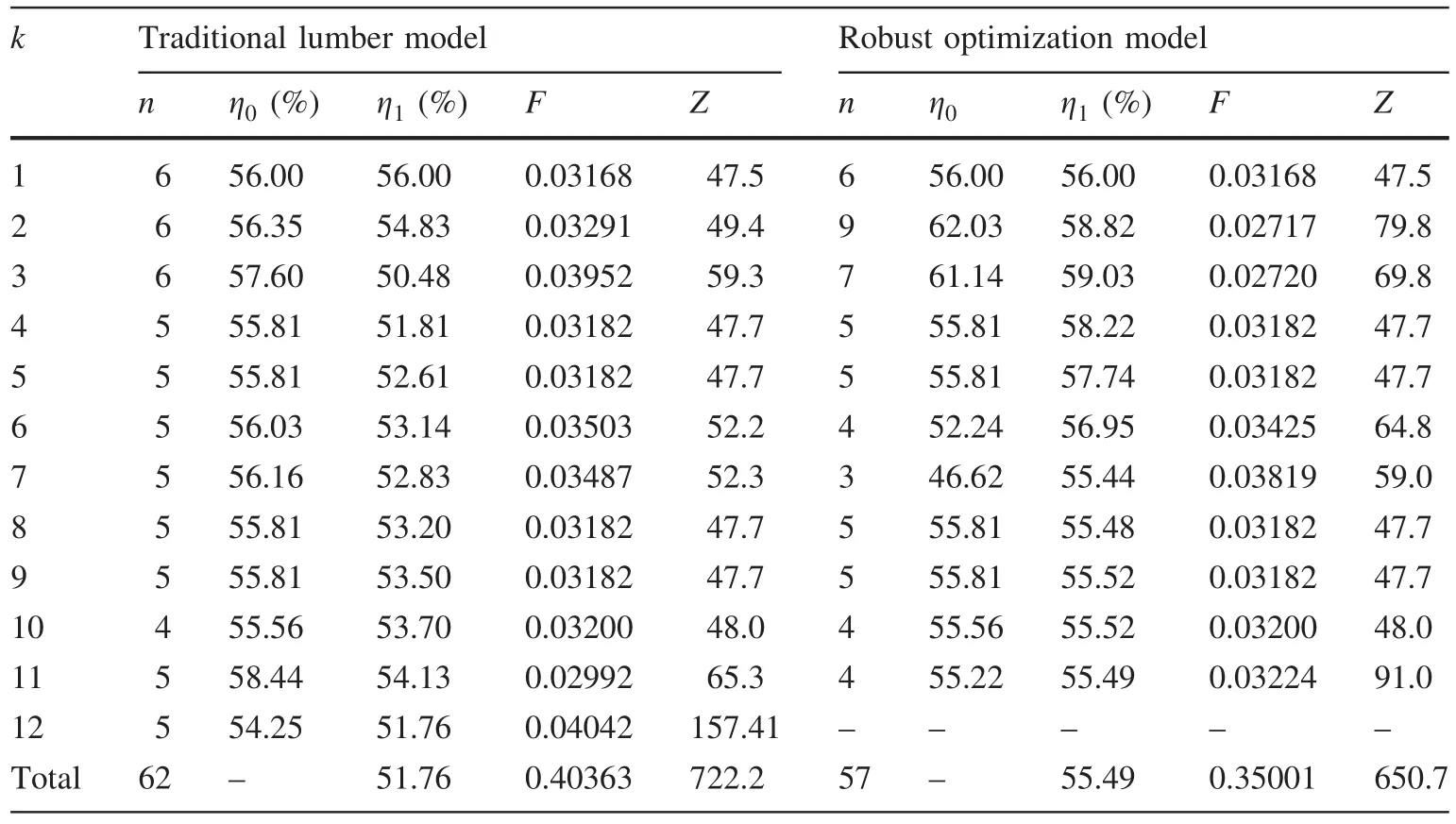
Table 4 Indexes of variation problem of lumber before and after optimization

In Table 4,we can determine that the variation ratio is somewhat greater for the sawn timber volume of per log in the robust optimization model than the traditional timber processing model.It shows that the robust optimization model is controlling the variation problem of lumber by sacri ficing the smoothness of sawmilling.There are 57 boards in the robust optimization model for timber processing,using 11 logs,with total by-product volume reduction from 0.40363 to 0.35001 m3,an improvement of 0.05362 m3.The manufacturing cost penalty was reduced from 722.2 to 650.7 Yuan(CNY),71.5 Yuan(CNY)better than before.The total output of boards raises from 51.76 to 55.49,a 3.73%improvement.

Conclusion

We evaluated the volume variation of raw material logs in timber processing and set up a robust optimization model.We developed a solution with the robust optimization approach and found the relationship between boards and raw material logs in timber processing.We optimized the results,showing that robust optimization can control the volume variation in timber processing,reduce by-product volume,and lower the manufacturing cost penalty.Sawmill enterprises using these research results are able to easily determine the relationship between the requirement of the robust model and timber

processing and choose a flexible method of timber processing,which could lower cost.We are able to supply theoretical evidence and references to solve uncertain parameter controlling problems for similar enterprises or similar processes in manufacturing.With the natural forest closed for commercial felling,a rational use of the robust optimization approach can improve the output of boards and maximize the log usage,which will help to protect forest resources

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License(http://crea tivecommons.org/licenses/by/4.0/),which permits unrestricted use,distribution,and reproduction in any medium,provided you give appropriate credit to the original author(s)and the source,provide a link to the Creative Commons license,and indicate if changes were made.

Alem DJ,Morabito R(2012)Production planning in furniture settings via robust optimization.Comput Oper Res 39(2):139–150

Alvarez PP,Vera JR(2014)Application of robust optimization to the sawmill planning problem.Ann Oper Res 219(1):457–475

Ben-Tal A,Nemirovski A (2000)Robust solutions of Linear Programming problems contaminated with uncertain data.Math Program 88(3):411–424

Bental A,Goryashko A,Guslitzer E,Nemirovski A(1999)Robust solutions to uncertain linear programs.OR Lett 25(1):1–13

Bertsimas D,Sim M(2003)Robust discrete optimization and network flows.Math Program 98(1):49–71

Bertsimas D,Sim M(2004)Robust discrete optimization and downside risk measures.National University of Singapore,working paper

Bertsimas D,Sim M(2004b)The price of robustness.Oper Res 52(1):35–53

Leung SCH,Chan SSW(2009)A goal programming model for aggregate production planning with resource utilization constraint.Comput Ind Eng 56(3):1053–1064

Liu SC,Lin CC(2005)A heuristic method for the combined location routing and inventory problem.Int J Adv Manuf Technol 26(4):372–381

Maturana S,Pizani E,Vera J(2009)Scheduling production for a sawmill:a comparison of a mathematical model versus a heuristic.Comput Ind Eng 59(4):667–674

Soyster AL(1973)Convex programming with set-inclusive constraints and applications to inexact linear programming.Oper Res 21(5):1154–1157

Varas M,Maturana S,Pascual R,Vargas I,Vera J(2014)Scheduling production for a sawmill:a robust optimization approach.Int J Prod Econ 150(6):37–51

Zanjani MK,Kadi DA,Nourelfath M(2010)Robust production planning in a manufacturing environment with random yield:a case in sawmill production planning.Eur J Oper Res 201(3):882–891