Abdelhalim Ebaid,Abdul-Majid Wazwaz,Elham Alali,and Basem S.MasaedehDepartment of Mathematics,Faculty of Science,University of Tabuk,P.O.Box 74,Tabuk 749,Saudi Arabia

2Department of Mathematics and Computer Science,Saint Xavier University,Chicago,IL 60655,USA

1 Introduction

In the field of boundary layer flow and heat transfer of nanofluids,[1?8]many scientific problems are governed by partial differential equations.By using the similarity variable η,these partial differential equations are then transformed into a set of ordinary differential equations with variable coefficients of exponential orders of the form e?βη(β ＞ 0),i.e.,non-polynomial types.In order to solve such ordinary differential equations,the authors often transform the resulted equations to ODEs of polynomial coefficients with the help of a new variable t= γ e?βη,where β and γ are physical parameters that are related to the mathematical formulations.For examples,Ebaid and Al Sharif[7]have obtained the following second-order ODE

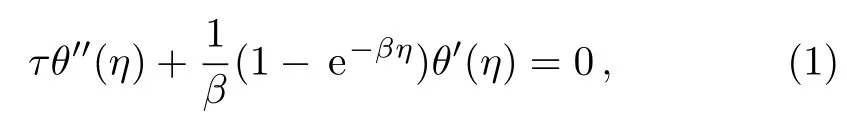
subject to the boundary conditions:

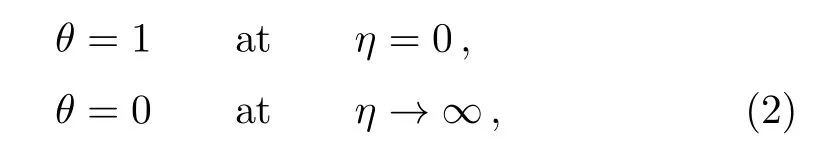
to describe the heat transfer of carbon-nanotubes over a stretching sheet.For details of the parameters β and τ,see please Ref.[7].On using the new variable t=e?βη(γ=1),Eq.(1)is transformed into the following ODE of polynomial coefficients[Ref.[7],Eq.(12)]

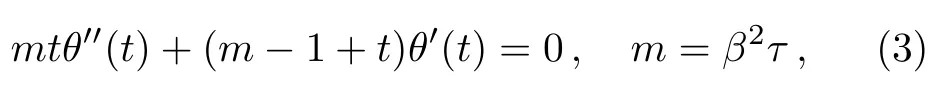
subject to the transformed boundary conditions:

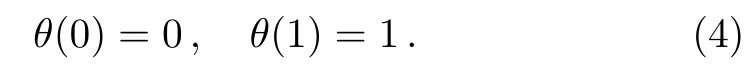
Another example was discussed by Kameswaran et al.,[Ref.[2],Eqs.(32)–(33)],who have used the variable

t= ?Pr?e?sη(β =s, γ = ?Pr?)and therefore obtained the following second-order ODE with polynomial coefficients for the temperature of nanofluids:

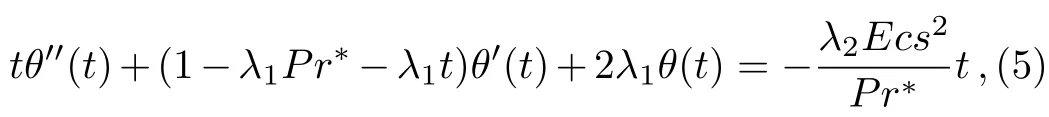
subject to boundary conditions:

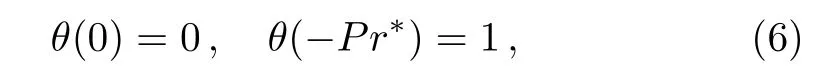
where the definitions of the parameters λ1,λ2,Pr?,Ec,and s have been addressed by Kameswaran et al.[2]

A main observation of these studies is that the temperature of nanofluids and the nano-particles concentration are usually governed by second-order ordinary differential equations.In this paper,we consider a generalized secondorder ordinary differential equation of the temperature of nanofluids θ(t)in the form:

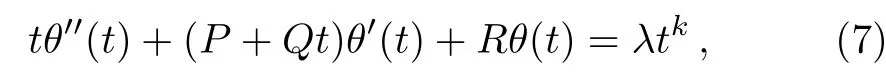
subject to the following set of boundary conditions

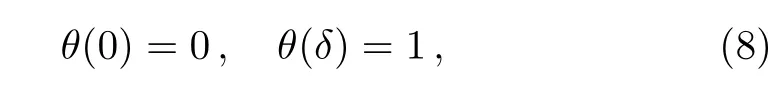
where P,Q,and R are physical parameters which are related to the thermal conductivities,the densities,and the heat capacitances of the base- fluids and the nanofluids.[1?8]The constant k is real and it takes a particular value according to the final form of the temperature equation.While the parameter δ depends upon the boundary condition of the temperature of the investigated problem.

The objective of this work is to introduce an analytical procedure to obtaining the closed-form solution of Eqs.(1)–(2).Such closed-form solution will be then implemented to establish the exact solutions of some wellknown problems in the field of nanofluids as special cases of the current generalized analytical solution.The suggested approach depends mainly on the Laplace transform technique.In the next section,the proposed method will be analyzed.Besides,applications of the current results on some well known nanofluids problems will be discussed in a subsequent section.Moreover,the obtained exact solutions for several problems are to be compared with the corresponding solutions in the literature.

2 Analytic Solution

In this section,an analytical procedure is to be presented to solve the second-order boundary value problem(7)–(8).Since Eq.(7)is a second-order linear ordinary differential equation with variable coefficient of polynomial type,it is then can be treated with Laplace transform.Assuming that Eq.(7)is non-homogenous,i.e.,λ/=0,then the general solution of Eq.(7)can be written as

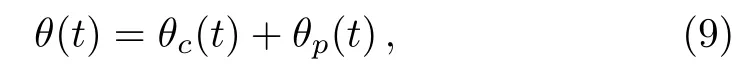
whereθc(t)andθp(t)are respectively the complementary solution and the particular solution.

2.1 The Complementary Solution

Consider the homogenous part of Eq.(7),we have

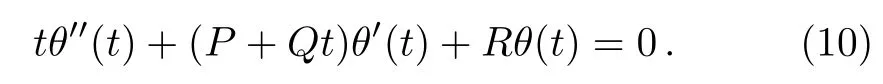
On applying Laplace transform to both sides of Eq.(10),it follows

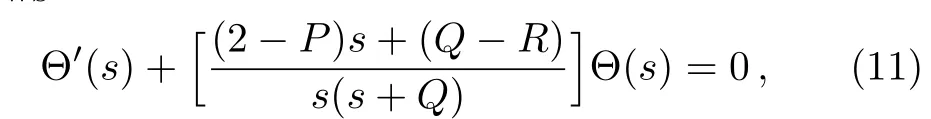
which can be re-written in the form

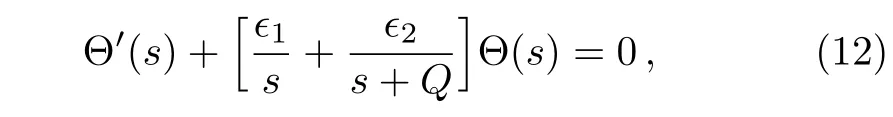
where

Integrating Eq.(12),we obtain

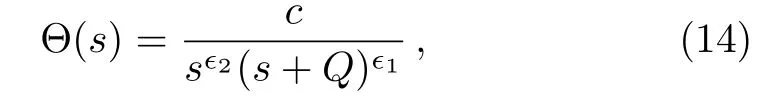
wherecis a constant of integration.On applying the inverse Laplace transform￡?1to Eq.(13),we obtain

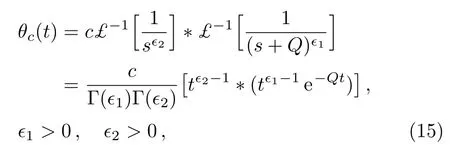
where?denotes to the convolution property defined by

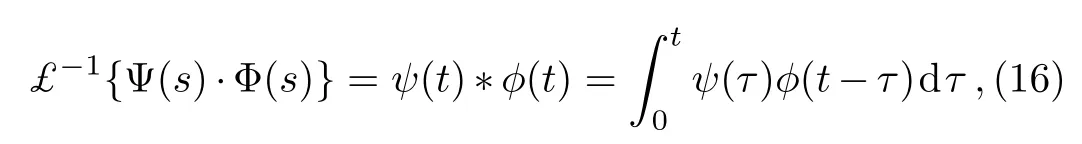
such that￡?1{Ψ(s)}=ψ(t)and￡?1{Φ(s)}=?(t).Accordingly,Eq.(14)becomes

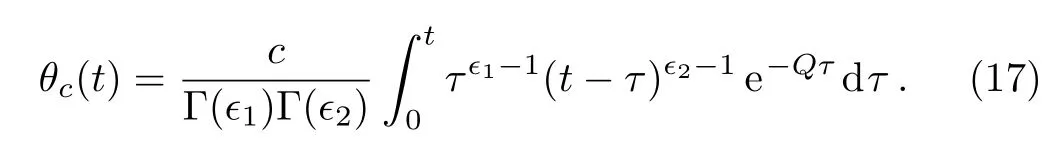
Changing the variable of integration usingτ=tμ,we get

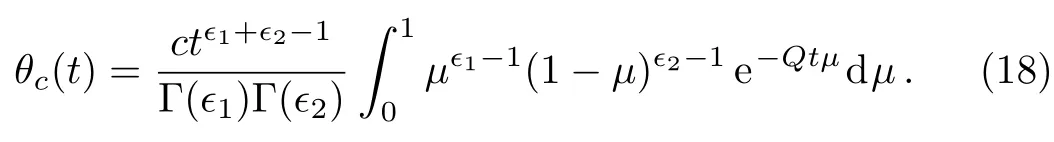
Therefore

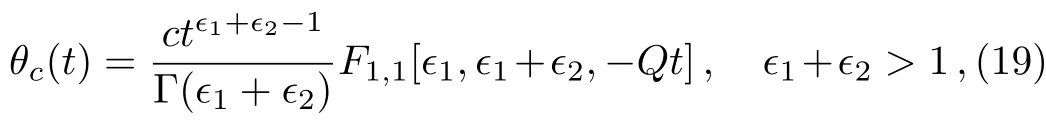
whereF1,1is Kummer’s function defined in its integral form by

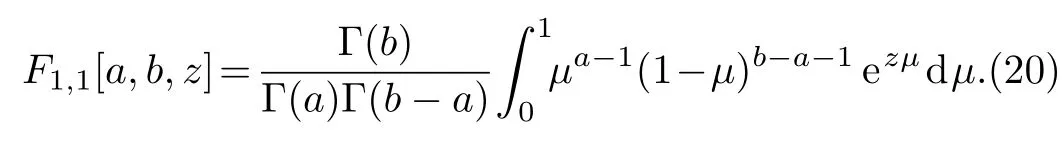
2.2 The Particular Solution

Regarding the particular solution,it can be assumed in the form

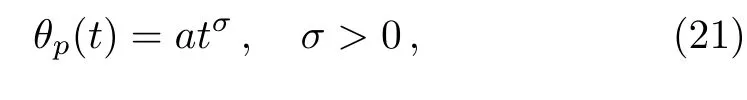
whereaandσare to be determined such that the assumption in Eq.(21)is a particular solution of Eq.(7).On substituting Eq.(21)into Eq.(7)and collecting terms of like powers,we have

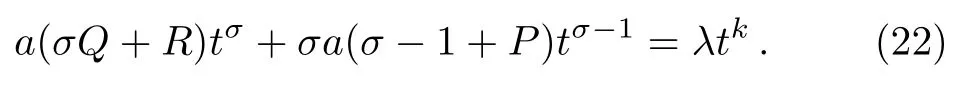
Two different particular solutions can be derived from Eq.(23)as follows,

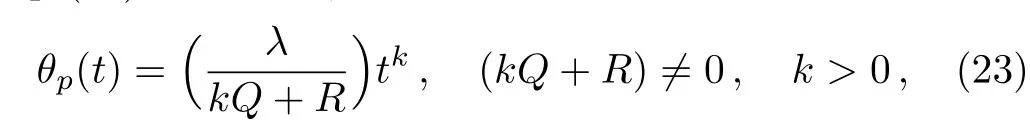
for the ODE:

or

for the ODE:

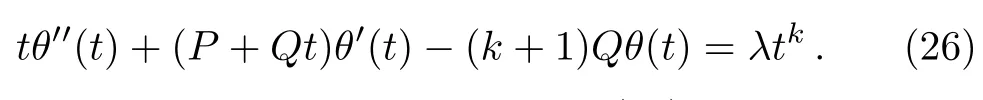
According to the particular solution(25),the general solution(9)becomes

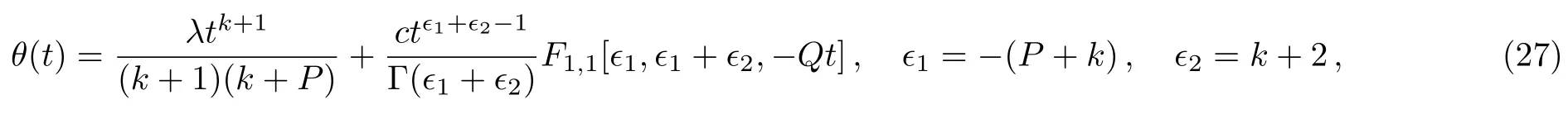
as a general solution for the ODE given by Eq.(26).

The solution given by Eq.(27)can be further simplified as

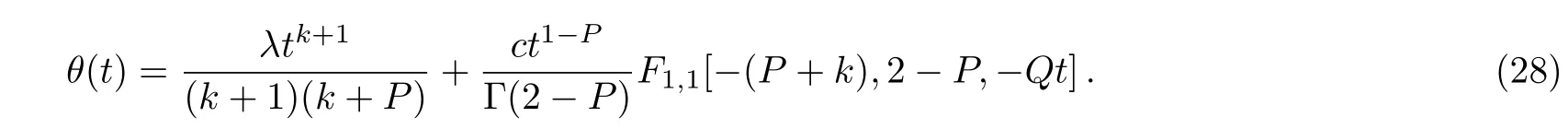
Here,it should be noted that the restrictions in Eq.(15)on?1and?2finally imply that

so that the boundary conditionθ(0)=0 is satisfied under the condition that?1＜k＜?P.Besides,the boundary conditionθ(δ)=1 givescby

Hence,

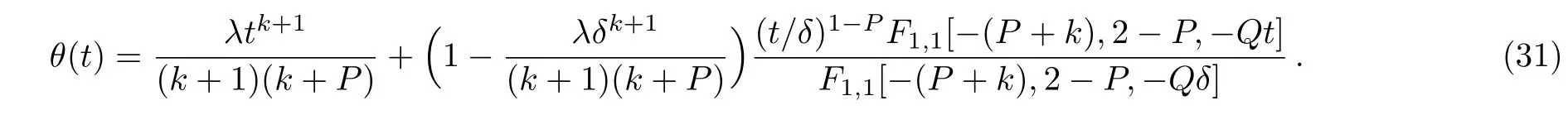
This exact solution satisfies Eq.(26)and the boundary conditions(8),which can be easily verified by direct substitution.Furthermore,it will be proved in the next section that such analytic solution reduces to the corresponding solutions in the literature as special cases.

3 Applications

3.1 Heat Transfer of Carbon-Nanotubes

The heat transfer of carbon-nanotubes is governed by the homogenous ODE given by Eqs.(3)–(4).In this case we haveλ=0,and therefore the general solution of Eqs.(3)–(4)is only given by the complementary solution as

where

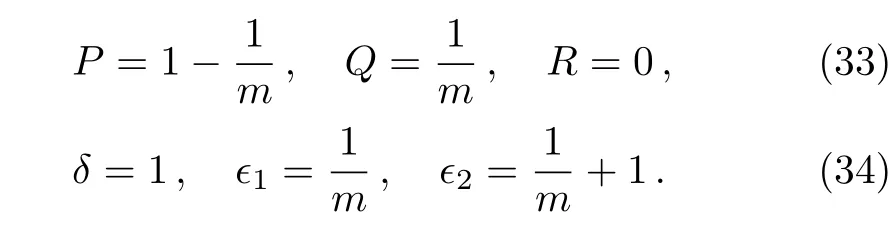
Therefore,the solution(32)reduces to

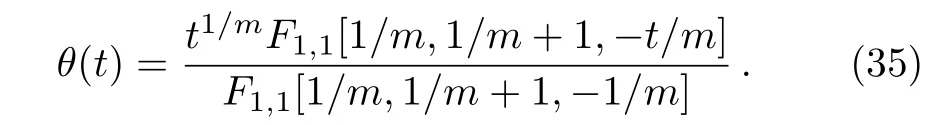
However

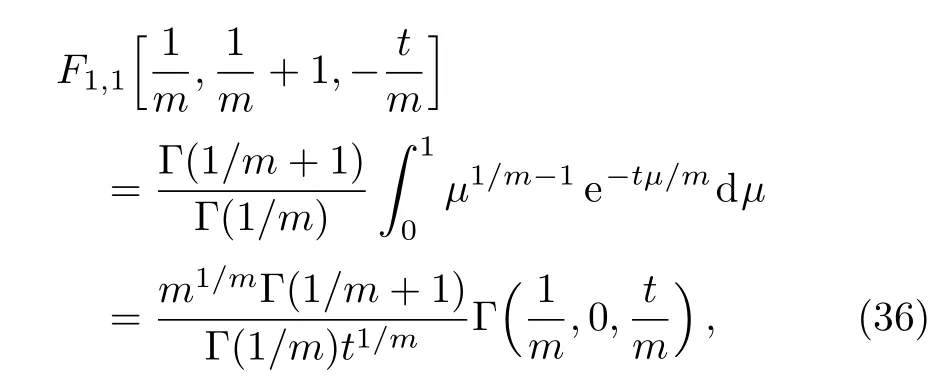
where

is the generalized incomplete gamma function used in Refs.[3–4,6–8].Further,we have

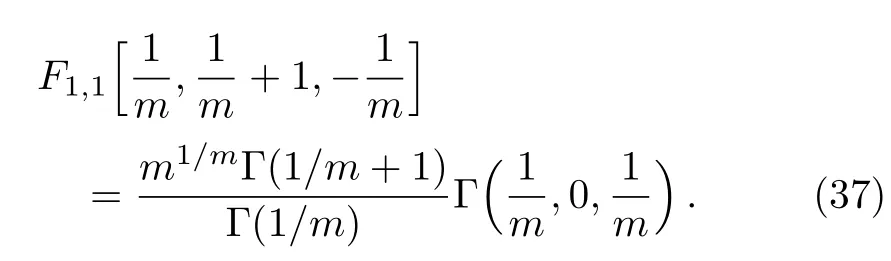
Inserting Eqs.(36)and(37)into Eq.(35),it then follows

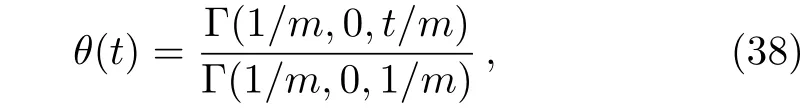
which is the same result obtained by Ebaid and Al Sharif[Ref.[7],Eq.(19)].

3.2 Heat Transfer of Cu-Water and Ag-Water Nanofluids

Kameswaranet al.[2]have derived Eqs.(5)–(6)for the heat transfer of the Cu-water and the Ag-water nanofluids over a stretching sheet.On comparing Eqs.(5)and(26),we have

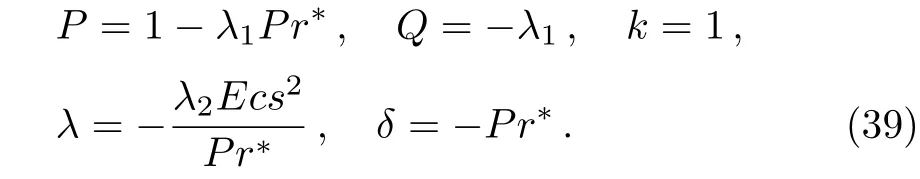
Also,Kameswaranet al.[2]definedPr?,α,andtas

On inserting Eqs.(39)–(40)into Eq.(30)we obtain the following exact solution for Eqs.(5)–(6):

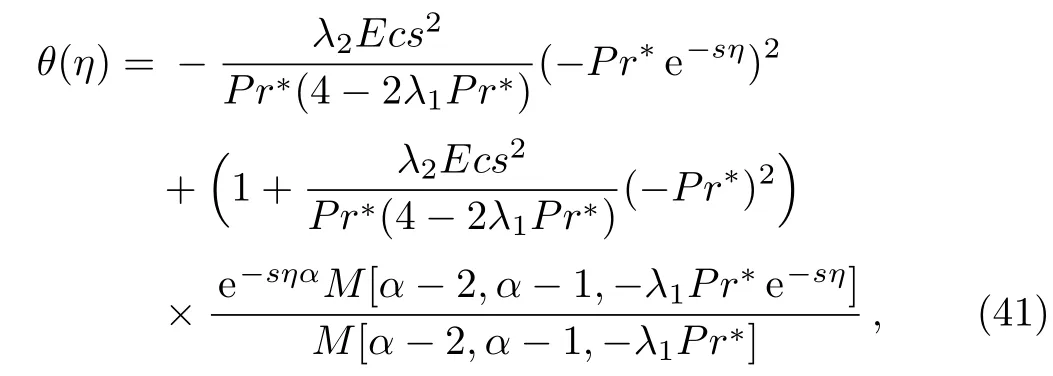
whereM[a,b,z]denotes also to Kummer’s functionF1,1[a,b,z]. Equation(41)is the same expression obtained by Kameswaranet al.(Eq.(36)in Ref.[2])for the temperature distribution as a special case of the current results.Furthermore,the exact solution derived above by Eq.(41)can be easily verified by direct substitution into Eq.(9).The Laplace transform has many advantages over the other methods which can be summarized as follows.It is well know that many standardized differential equations of second-order with variable coefficients have well known solutions such as Kummer’s equation,Airy’s equation,Legendre’s equation,Bessel’s equation,...,etc.However,if the investigated differential equation is of different form than those mentioned above we have in that case to search for another method of solution.Since most of the differential equations are of forms differ than those mentioned above,then Laplace transform is one of the effective tools to achieve this task.

4 Conclusion

In this paper,the exact solution of a class of secondorder ordinary differential equations with variable coeffi-cients arises in nanofluids has been obtained.The generalized analytical solution is expressed in terms of the hypergeometric series.The obtained results have been applied on selected problems in nanofluids and therefore compared with those in the literature.At particular choices for the coefficients,the current class reduces to similar published boundary value problems.Hence,the corresponding solutions in the literature were derived as special cases of our generalized analytical solution.

5 Conflict of Interest

The author(s)declare(s)that there is no conflict of interest regarding the publication of this paper.

[1]M.A.A.Hamad,Int.Commun.Heat.Mass.Transf.38(2011)487.

[2]P.K.Kameswaran,M.Narayana,P.Sibanda,and P.V.S.N.Murthy,Int.J.Heat.Mass.Transf.55(2012)7587.

[3]E.H.Aly and A.Ebaid,Abstr.Appl.Anal.2013(2013)1.

[4]E.H.Aly and A.Ebaid,J.Comput.Theor.Nanosci.10(2013)2591.

[5]W.A.Khan,Z.H.Khan,and M.Rahi,Appl.Nanosci.4(2014)633.

[6]A.Ebaid,F.Al Mutairi,and S.M.Khaled,Adv.Math.Phys.2014(2014)1.

[7]A.Ebaid and M.Al Sharif,Z.Naturforsch.A 70(2015)471.

[8]E.H.Aly and A.Ebaid,J.Mol.Liq.215(2016)625.