Wang Rui,Liu Jinkun

School of Automation Science and Electrical Engineering,Beihang University,Beijing 100083,China

Adaptive formation control of quadrotor unmanned aerial vehicles with bounded control thrust

Wang Rui,Liu Jinkun*

School of Automation Science and Electrical Engineering,Beihang University,Beijing 100083,China

Adaptive control;Bounded input;Formation control;Parametric uncertainties;Quadrotor UAV;Unit-quaternions

In this paper,the flight formation control problem of a group of quadrotor unmanned aerial vehicles(UAVs)with parametric uncertainties and external disturbances is studied.Unitquaternions are used to represent the attitudes of the quadrotor UAVs.Separating the model into a translational subsystem and a rotational subsystem,an intermediary control input is introduced to track a desired velocity and extract desired orientations.Then considering the internal parametric uncertainties and external disturbances of the quadrotor UAVs,the priori-bounded intermediary adaptive control input is designed for velocity tracking and formation keeping,by which the bounded control thrust and the desired orientation can be extracted.Thereafter,an adaptive control torque input is designed for the rotational subsystem to track the desired orientation.With the proposed control scheme,the desired velocity is tracked and a desired formation shape is built up.Global stability of the closed-loop system is proven via Lyapunov-based stability analysis.Numerical simulation results are presented to illustrate the effectiveness of the proposed control scheme.

1.Introduction

In recent years,formation control problems have become one of the leading research areas among the research community.Compared with a single vehicle,a group of vehicles that work cooperatively may provide a better performance and fulfill a more difficult task,which has been motivating further studies of formation control problems.In order to achieve formation control,consensus algorithms for multi-agent systems have been extensively studied in the literature,1–11and can be categorized as leader-follower,1–4behavior-based,5–7and virtual structure.8–11

Nevertheless,these works of consensus algorithms referred above mainly considered simple models such as single or double integrators.Since a quadrotor unmanned aerial vehicle(UAV)isamorecomplexsystem with characteristics of multi-variable,nonlinear,strong coupling,and underactuation, its formation control problems are more complicated than those of simple models.Fortunately,with the development of technology and the increasing demand for formation control of robot systems,researchers are tryingto deal with formation problems for complex systems using these approaches.

A consensus algorithm is designed3to enable quadrotor UAVs to fly in formation in a leader-follower structure,where artificial potential field functions are used to ensure collision avoidance.Galzi and Shtessel7proposed a sliding mode controller that achieved UAV formation tracking affected by unknown bounded disturbances,and three control strategies were presented:the ‘Tracking”strategy,the ‘Placement”strategy,and the ‘Anti-Collision” strategy.

Guerrero et al.9studied the quadrotor UAV formation problem with input saturation.Assuming that the angles are operated in a neighborhood of an origin,the model of a quadrotor UAV is simplified as a fourth-order integrator.A bounded control law was designed using the nested saturation technique.In addition,formation control problems with network communication delays have been studied,to control a team of micro-aerial vehicles moving quickly with time delays and communication failures in the network8,and to deal with bounded time-varying delays that can be arbitrarily fast using frequency domain design methods.10Wu and Shi11studied the consensus in multi-agent systems with random delays governed by a Markov chain,and found that with a sufficient condition given by a set of linear matrix inequalities(LMIs),the delays can be tolerated.

In practical situations,the mass of a quadrotor UAV is not fixed when equipped with different sensors for different missions or due to a payload con figuration change.Hence,intrinsic parameter uncertainties should be taken into consideration.Unfortunately,model parameters are generally uncertain and cannot be measured precisely.The general backstepping control method that depends on accurate system model parameters is invalid when facing model uncertainties.Besides,it will be unrealistic to measure the mass value and the moment of inertia value of the vehicle during a flight.Therefore,some adaptive controllers12–17for controlling a single vehicle are proposed to deal with uncertainties.

Apparently,extending the existing strategies proposed for simple multi-agent systems and single quadrotor UAVs to the formation control problem of quadrotor UAVs is not a trivial task.Although the control problems of a single quadrotor UAV with parameter uncertainties have been well discussed,the quadrotorUAV formation problem with uncertainties is not well taken into consideration.

The main contribution of this paper is to provide a formation control scheme for a group of quadrotor UAVs with parametric uncertainties and external disturbances.To deal with under-actuation of the quadrotor UAVs in the formation,a prior-bounded intermediary control input and the adaptive laws of the mass uncertainty and the external force disturbances are designed for position tracking,by which the bounded control thrust and the bounded desired orientation are extracted.Then,a control torque and the adaptive laws of the moment of inertia uncertainties and the external torque disturbances are designed to track the desired orientation in terms of the unit-quaternions.A novel Lyapunov function is constructed to determine the stability of the overall system.

The remainder of this paper is organized as follows.In Section 2,the dynamic model of the quadrotor UAVs and some definitions and assumptions are given.In Section 3,the control laws and adaptive laws are proposed.In Section 4,global stability of the closed-loop system is proven via Lyapunov-based analysis.In tion 5,simulation results are given to demonstrate the effectiveness of the control laws proposed above.Finally,the conclusions are given in Section 6.

2.System model and preliminaries

2.1.System model

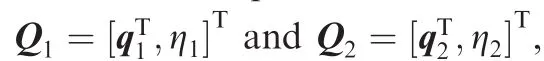
The physical structure of the quadrotor UAV is illustrated in Fig.1.

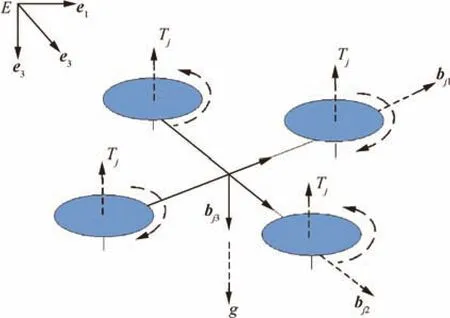
Fig.1 Physical structure of a quadrotor UAV.

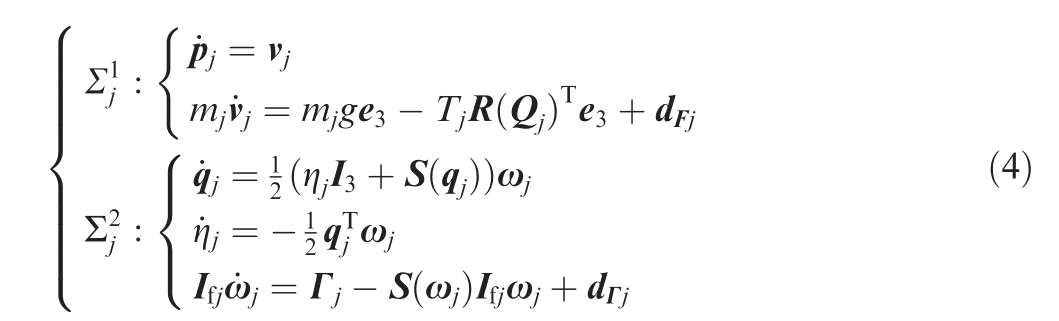
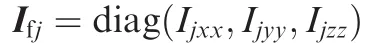
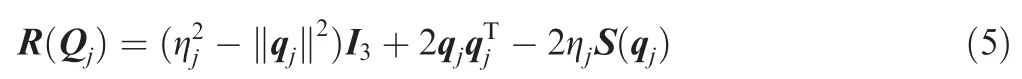
2.2.Preliminaries

This part presents the following necessary assumptions,which will be needed in the subsequent design and analysis of the formation control scheme.

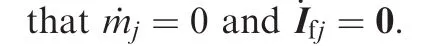
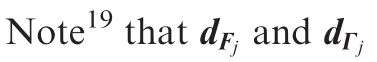
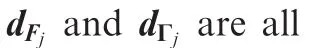
Assumption 5.Graph theory is used to describe the communication links between the quadrotor UAVs in the formation,where the information flow between members in the formation is assumed to be fixed and undirected,and is described by weighted graphs.

Definition 1.Graph20theory.

If there is a path between any two distinct nodes of a weighted undirected graph#,then#is connected.

2.3.Problem formulation

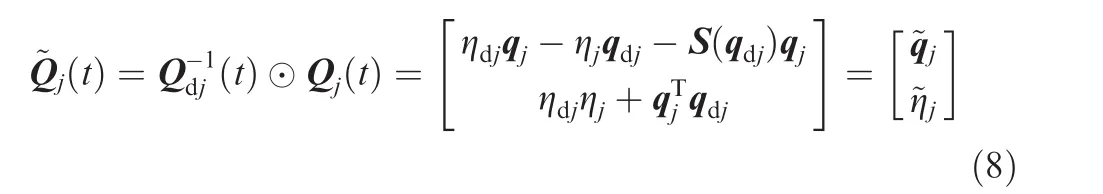
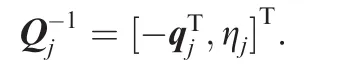
Our control objective is to design an adaptive controller for each quadrotor UAV in the formation to keep a desired flight formation shape and to track the common reference velocity vdin the three-dimensional space with parametric uncertainties and external disturbances.

3.Formation control design

3.1.Controller design for translational subsystem

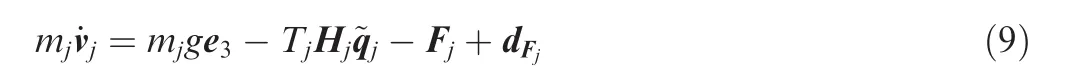
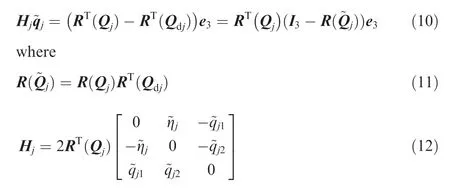
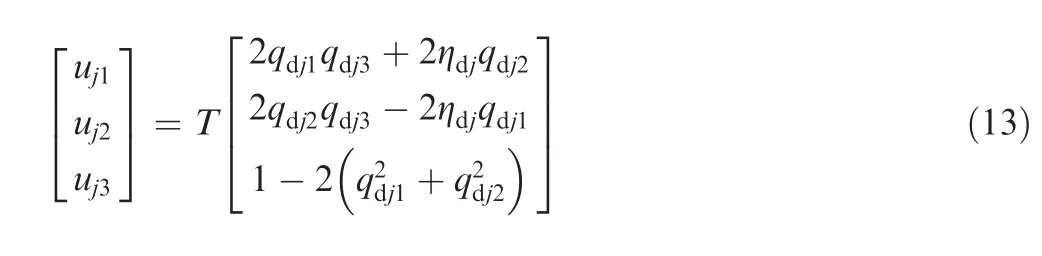
It is clear that Eq.(13)has multiple solutions of the desired orientation Qdjand the control thrustTjin terms of Fj.To get a group of unique solutions,letqdj3?0,and then we obtain

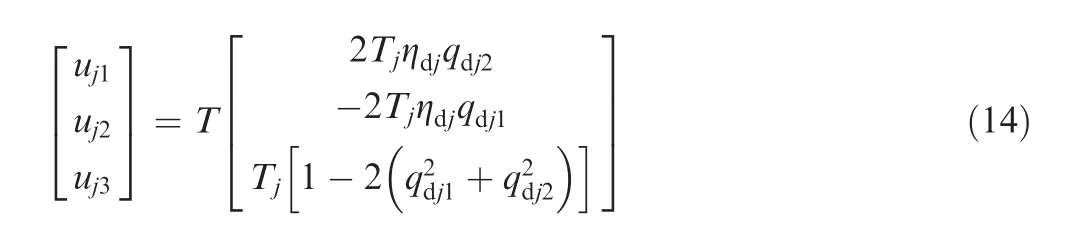
Taking the sum of the squares of the first two equations of Eq.(14),we obtain

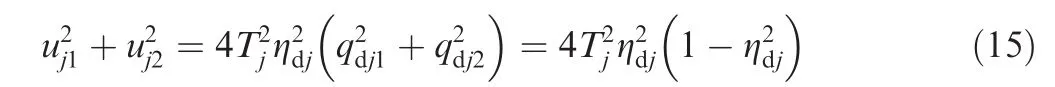
One possible solution for Eq.(15)is that

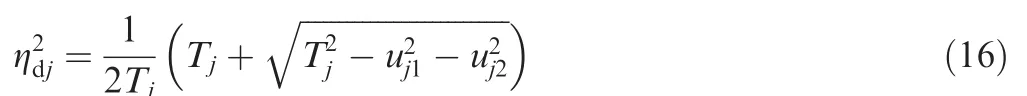
Submitting Eq.(1)into the last equation of Eq.(14),we obtain

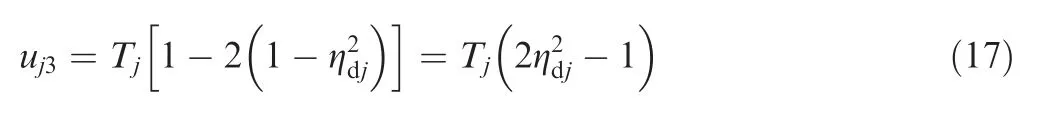
Exploiting Eq.(17)with Eq.(16),we have

So we can extract the thrust magnitudeTjas

Then we can extractqdj1andqdj2by using the first two equations of Eq.(14)as

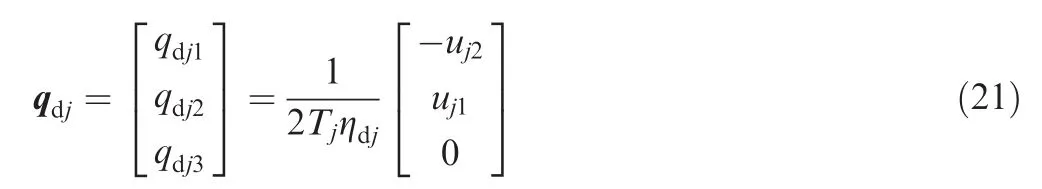
The desired angular velocity xdjcan be obtained as21

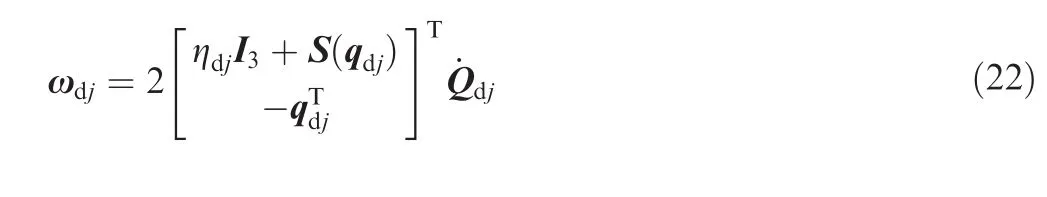
Consequently,for thejth UAV in the formation,the intermediary control law Fjfor the translational subsystem could be designed at first.Then using the extraction method Eqs.(19)–(22)withqdj3? 0,we can getTj,qdj1,qdj2and gdj.Finally,the control law for the rotational subsystem could be further designed to track the desired orientation.The diagram of the control scheme is illustrated in Fig.2.

From Eqs.(7)and(9),the velocity error differential equation of the rotational subsystem can be written as

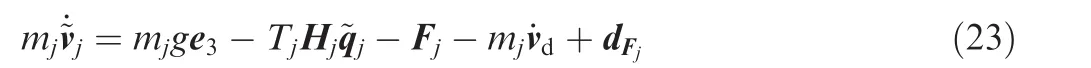
The control input for thejth quadrotor is proposed as follows

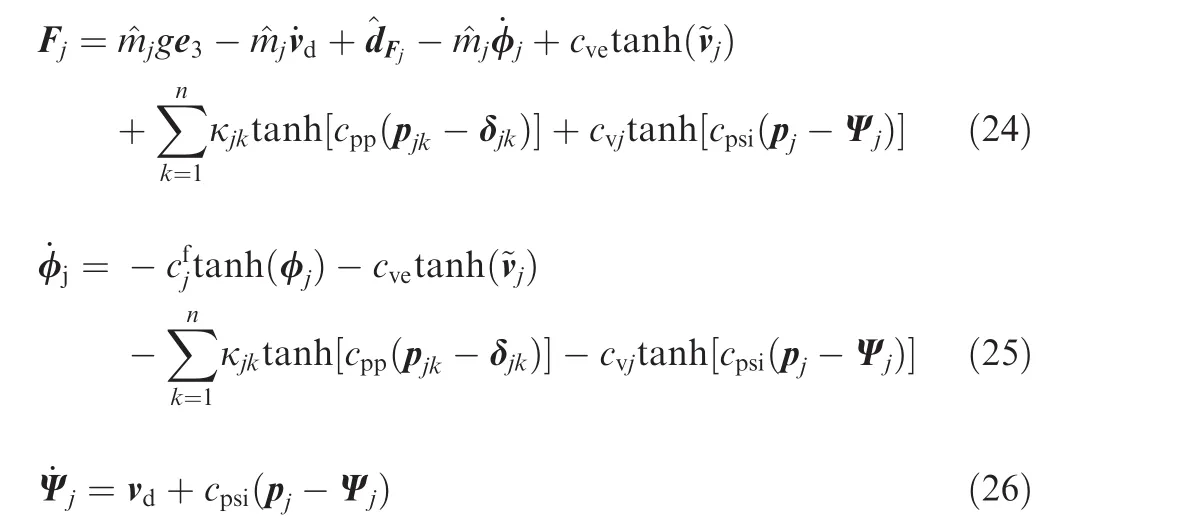
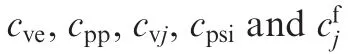
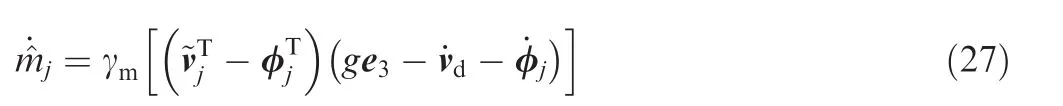
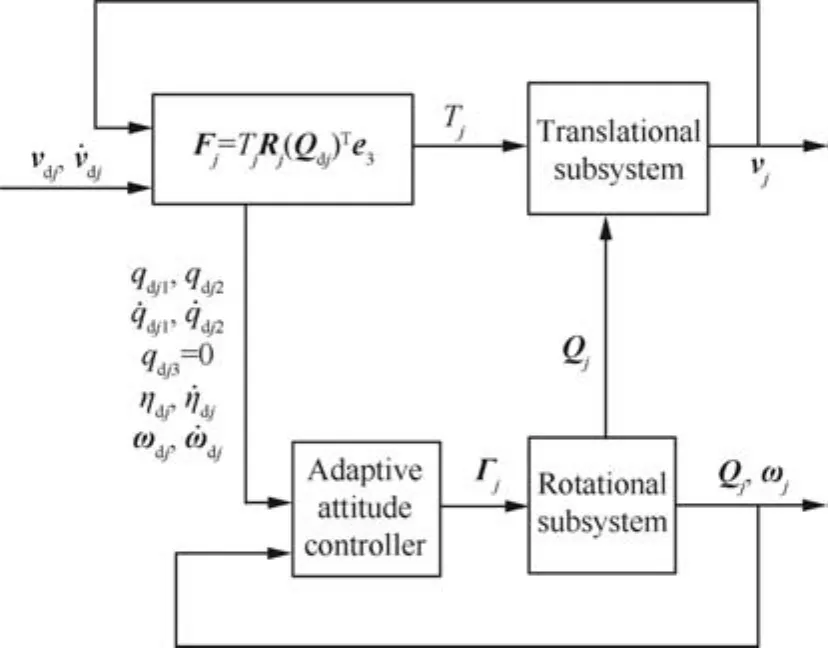
Fig.2 Diagram of control scheme.

3.2.Control design for rotational subsystem

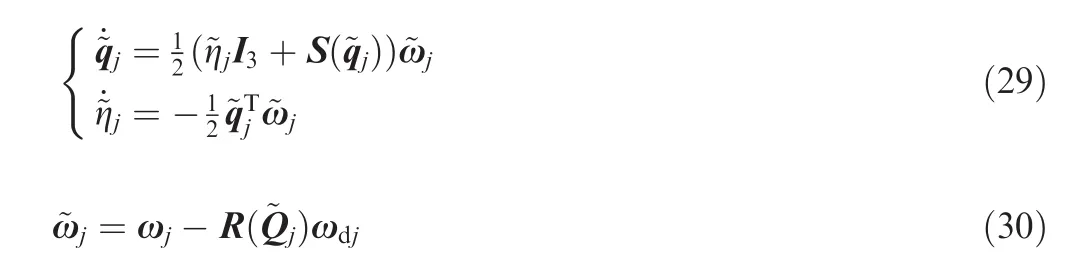
The quaternion error kinematics can be derived by using Eqs.(4)and(8)as

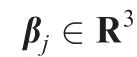
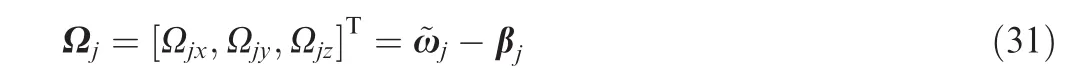
Taking the time derivative of Eq.(31),we have

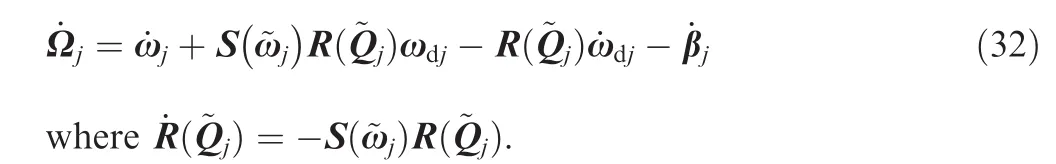
Then the closed-loop tracking error of the rotational subsystem can be written as

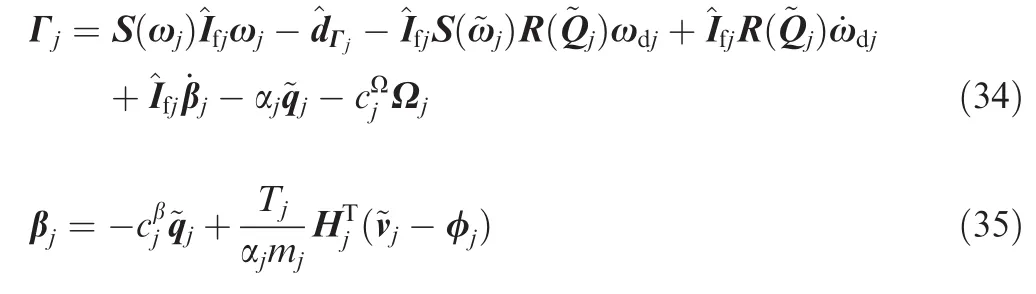
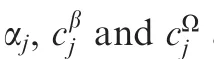
Taking the time derivative of Eq.(35),we obtain

where

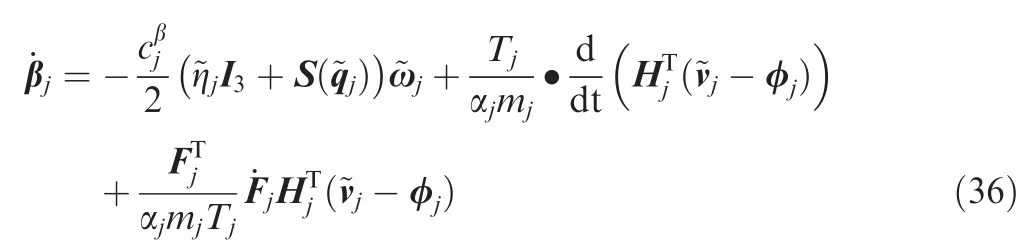
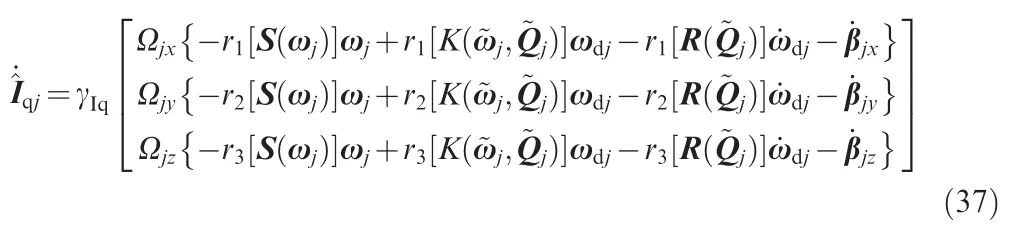
4.Stability analysis

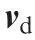
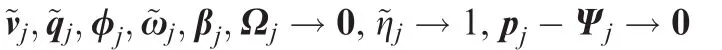
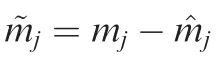
Choose the following Lyapunov function candidate

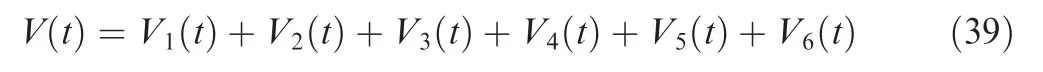
in which

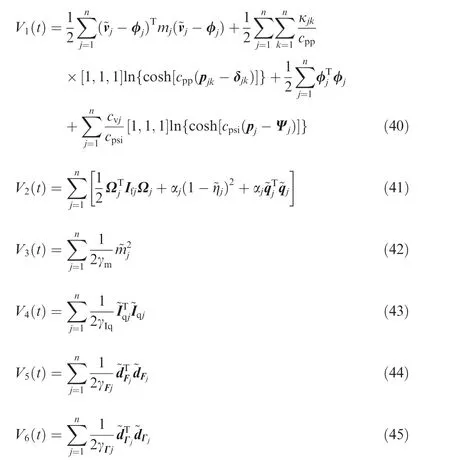
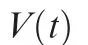
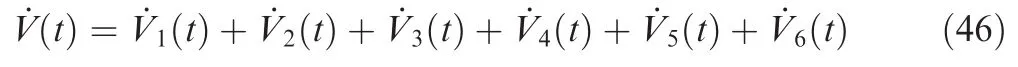
where

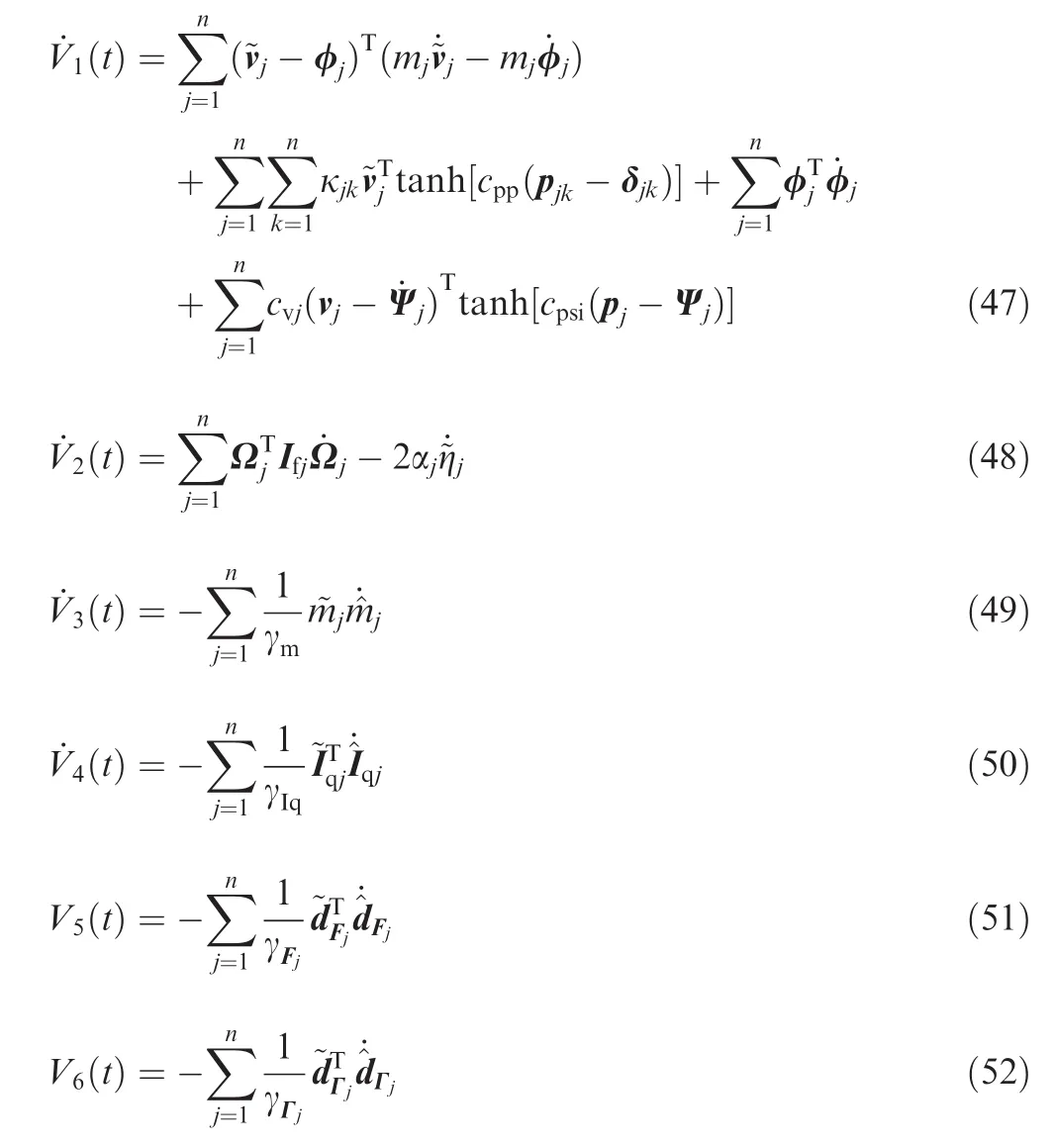
Submitting Eq.(29)into Eq.(48)with the error Eqs.(23)and(33),we can obtain the time derivative of the Lyapunov function as

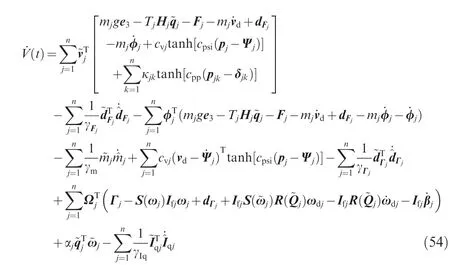
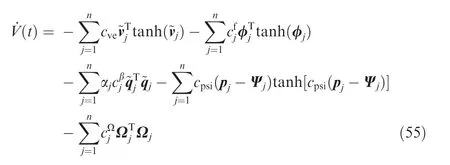
Then we have

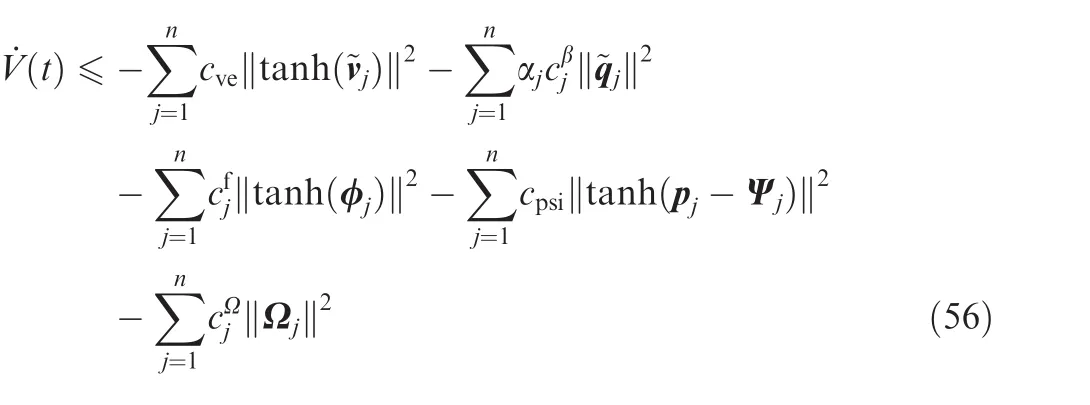
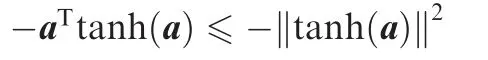
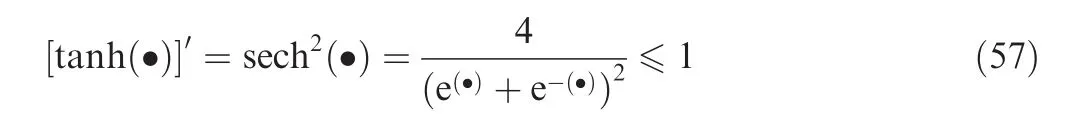
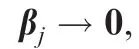
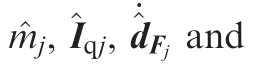
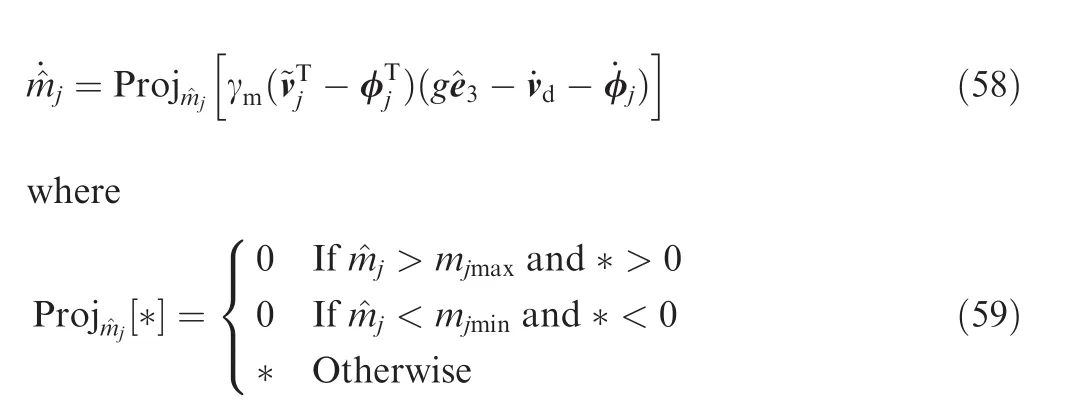
and Eq.(37)is revised to

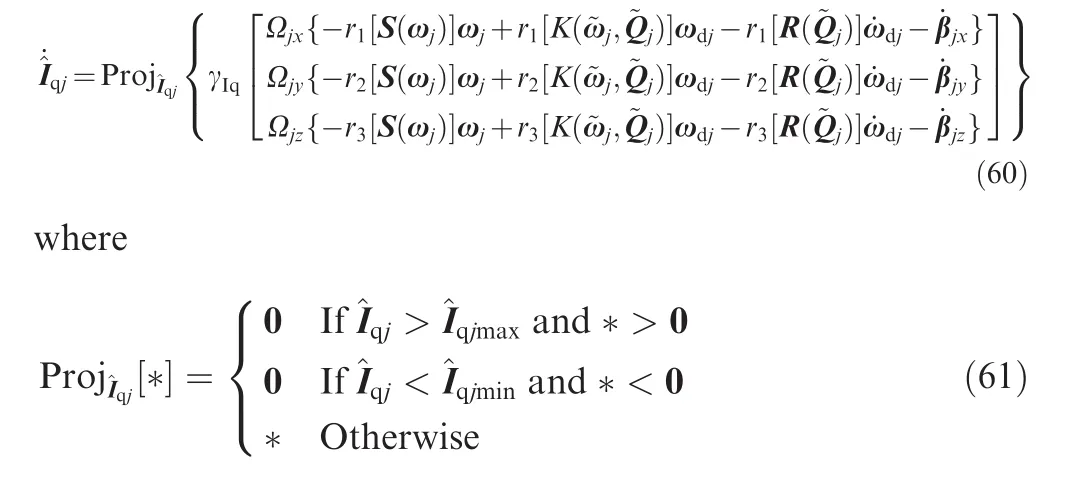
Similar to Eqs.(58)–(61),Eq.(28)is revised to

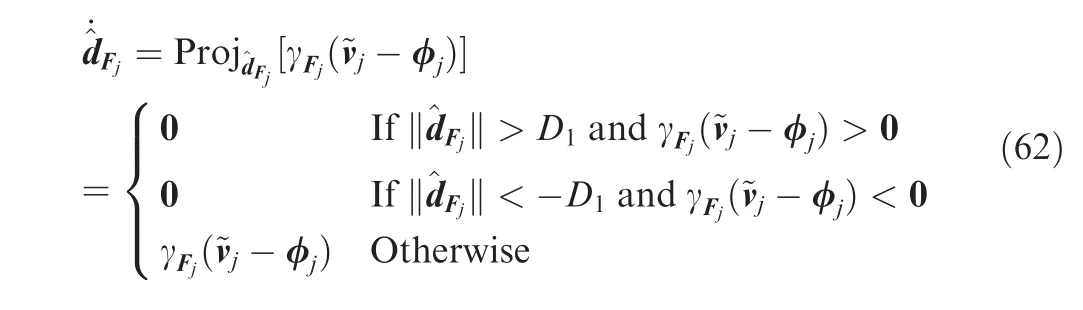
and Eq.(38)is revised to

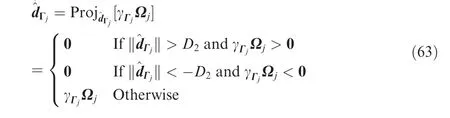
Using the extraction process Eqs.(19)–(22),we obtainTj,qd,gdand xdare bounded as priori.Therefore,the control thrust inputs for the quadrotor UAVs in the formation are all bounded.

5.Simulations

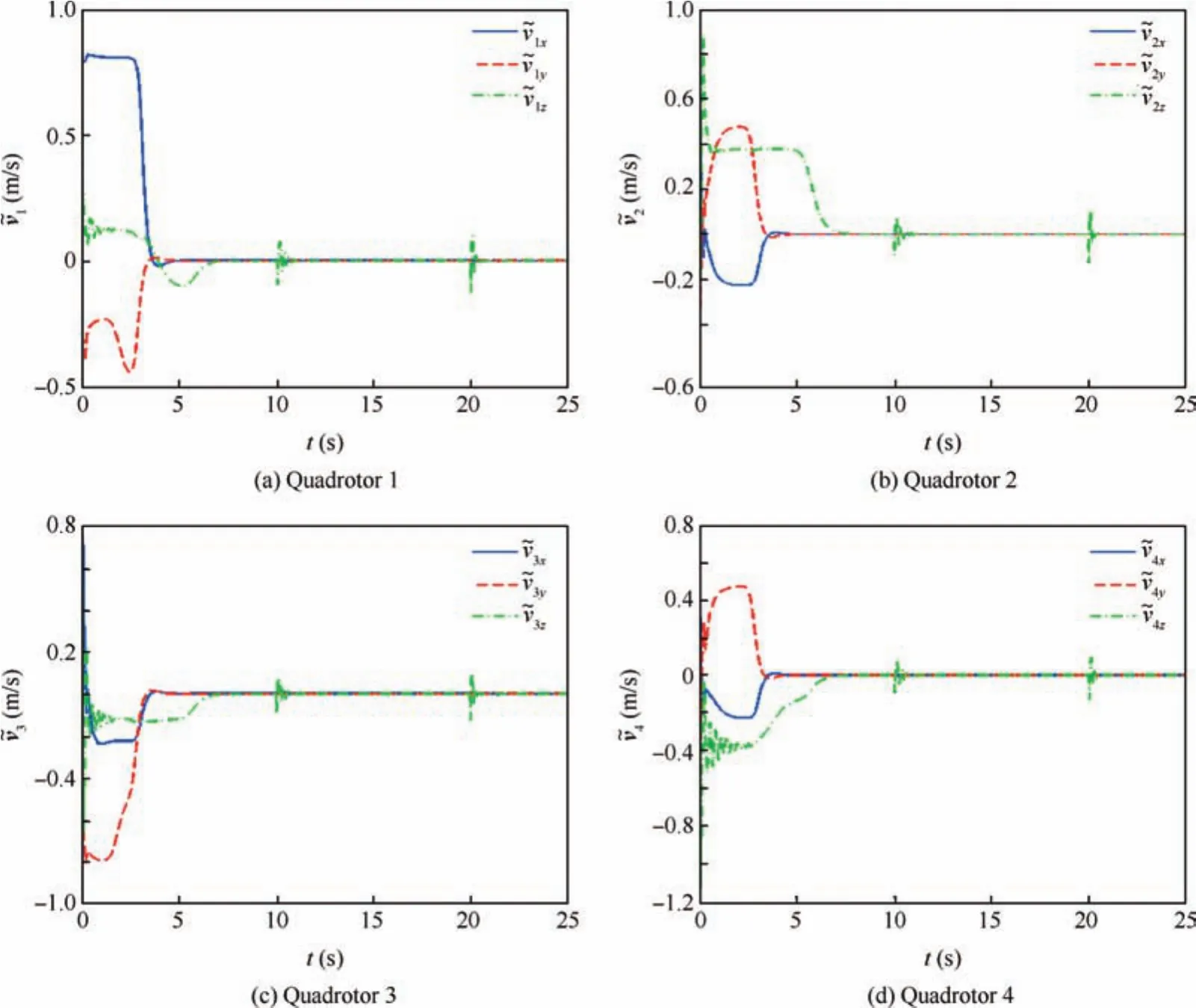
Fig.3 Velocity tracking errors of four quadrotor UAVs.

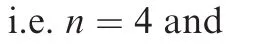
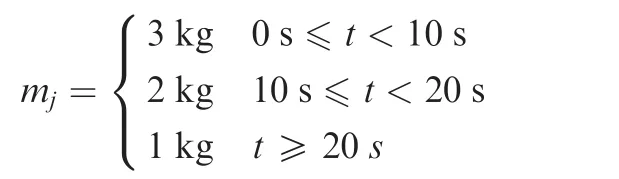
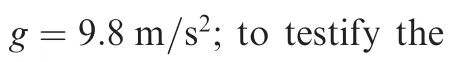
to testify the effectiveness of the adaptive laws Eqs.(28)and(38),the disturbances are given by

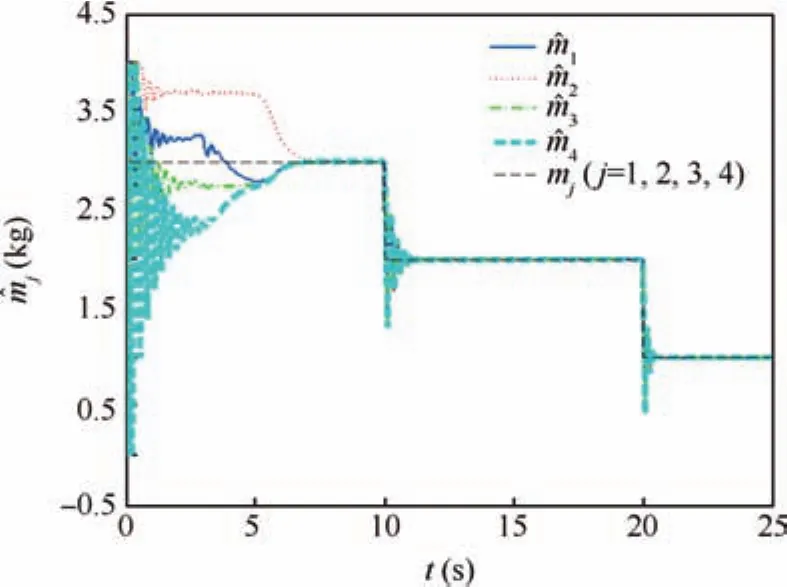
Fig.5 Adaptive output of each quadrotor UAV.

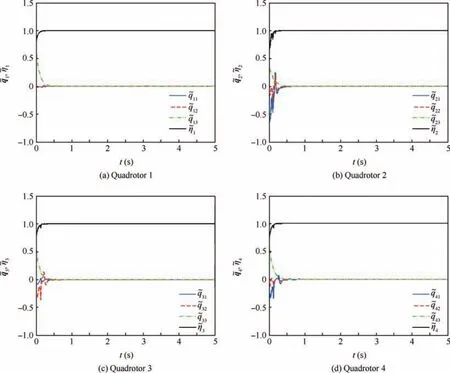
Fig.4 Quaternion tracking errors of four quadrotor UAVs.

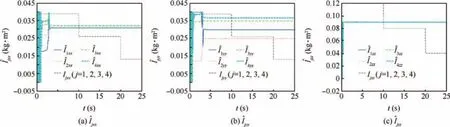
Fig.6 Adaptive output of each quadrotor UAV.

6.Conclusions

In this paper,the formation control problem of a group of quadrotor UAVs with parametric uncertainties and external disturbances is considered.The main contributions are as follows:

Fig.7 Adaptive output of each quadrotor UAV.

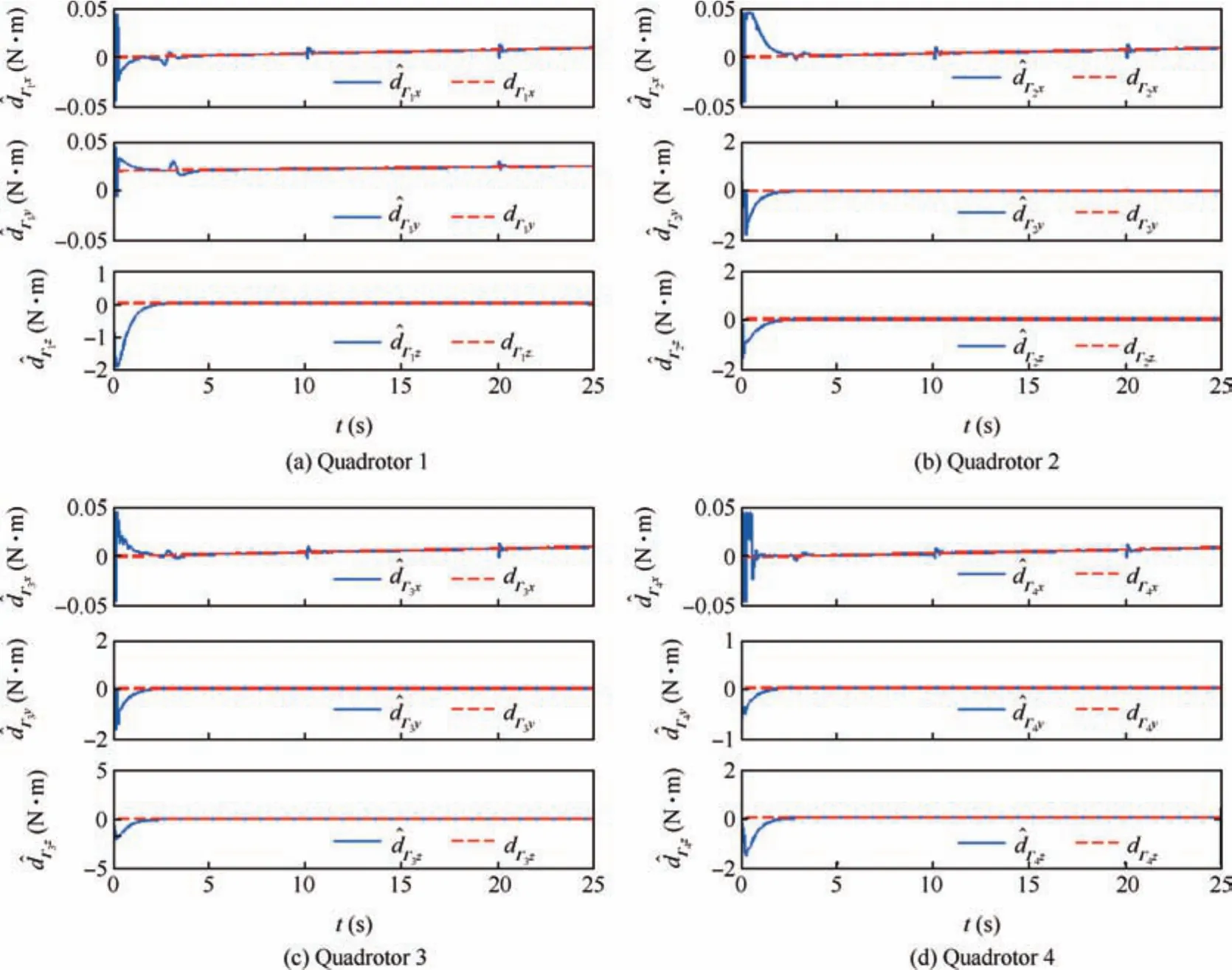
Fig.8 Adaptive output of each quadrotor UAV.

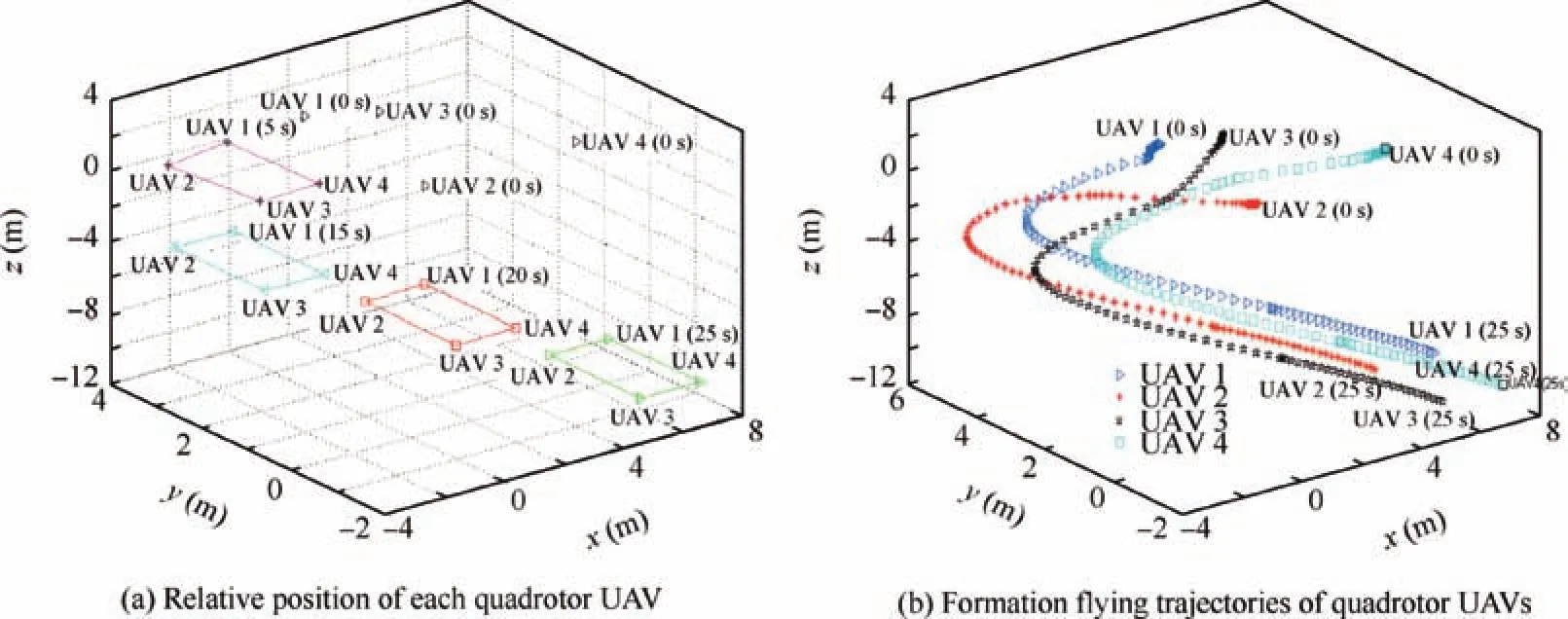
Fig.9 Formation process of four quadrotor UAVs.

(1)An adaptive control scheme for each vehicle is studied,where a bounded control thrust input,a control torque input,and four adaptive laws for the mass,the moment of inertia,and the external aerodynamic disturbances are proposed,so that all vehicles track a reference velocity and maintain a desired flight formation shape.

(2)Projection operators are employed for the design of the adaptive laws to ensure that the control thrusts and the adaptive parametric estimates remain bounded.

(3)Global stability of the closed-loop system is validated through both theoretical proof and simulation result.

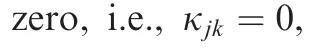
Acknowledgement

This research was supported by the National Natural Science Foundation of China(No.61374048).

1.Dierks T,Jagannathan S.Neural network control of quadrotor UAV formations.Proceedings of 2009 American Control Conference;2009 June 10–12;St.Louis.Piscataway(NJ):IEEE Press;2009.p.2990–6.

2.Mercado DA,Castro1 R,Lozano R.Quadrotors flight formation control using a leader-follower approach.Proceedings of 2013 European control conference(ECC);2013 July 17–19;Zurich.Piscataway(NJ):IEEE Press;2013.p.3858–63.

3.Kuriki Y,Namerikawa T.Consensus-based cooperative formation control with collision avoidance for a multi-UAV system.Proceedings of 2014 American control conference;2014 Jun 4–6;Portland,Oregon.Piscataway(NJ):IEEE Press;2014.p.2077–82.

4.Zhao W,Go T.Quadcopter formation flight control combining MPC and robust feedback linearization.J.Franklin Inst.2014;351(3):1335–55.

5.Balch T,Arkin RC.Behavior-based formation control for multirobot teams.IEEE Trans Robot Automat1998;14(6):926–39.

6.Lawton JRT,Beard RW,Young BJ.A decentralized approach to formation maneuvers.IEEETrans Robot Automat2003;19(6):933–41.

7.Galzi D,Shtessel Y.UAV formations control using high order sliding modes.Proceedings of 2006 American control conference;2006 Jun 14–16;Minneapolis.Piscataway(NJ):IEEE Press;2006.p.4249–54.

8.Turpin M,Michael N,Kumar V.Trajectory design and control for aggressive formation flight with quadrotors.Auton Robots2012;33(1):143–56.

9.Guerrero JA,Castillo P,Salazar S,Lozano R.Mini rotorcraft flight formation control using bounded inputs.J Intell Rob Syst2012;65(1):175–86.

10.Chen Y,Shi Y.Consensus for linear multiagent systems with timevarying delays:a frequency domain perspective.IEEE Trans Cybern2016;99:1–8.

11.Wu J,Shi Y.Consensus in multi-agent systems with random delays governed by a Markov chain.Syst Control Lett2011;60(10):863–70.

12.Yang C,Li Z,Cui R,Xu B.Neural network-based motion control of an underactuated wheeled inverted pendulum model.IEEE Trans Neural Netw Learn Syst2014;25(11):2004–16.

13.Aguiar AP,Hespanha JP.Trajectory-tracking and path-following of underactuated autonomous vehicles with parametric modeling uncertainty.IEEE Trans Autom Control2007;52(8):1362–79.

14.Huang M,Xian B,Diao C,Yang K.Adaptive tracking control of underactuated quadrotor unmanned aerial vehicles via backstepping.Proceedings of 2010 American control conference;2010 Jun 30–July 2;Baltimore.Piscataway(NJ):IEEE Press;2010.p.2076–81.

15.Nicol C,Macnab CJB,Ramirez-Serrano A.Robust adaptive controlof a quadrotor helicopter.Mechatronics2011;21(6):927–38.

16.Islam S,Dias J,Seneviratne LD.Adaptive tracking control for quadrotor unmanned flying vehicle.Proceedings of 2014 IEEE/ASME international conference on advanced intelligent mechatronics(AIM);2014 July 8–11.Piscataway(NJ):IEEE Press;2014.p.441–5.

17.Xu B,Yang C,Pan Y.Global neural dynamic surface tracking control of strict-feedback systems with application to hypersonic flight vehicle.IEEE Trans Neural Networks Learn Syst2015;26(10):2563–75.

18.Shuster MD.A survey of attitude representations.J Astronaut Sci1993;41(4):439–517.

19.Liu Z,Liu J,He W.Dynamic modeling and vibration control of a flexible aerial refueling hose.Aerosp Sci Technol2016;55:92–102.

20.Ren W,Beard RW.Consensus seeking in multiagent systems under dynamically changing interaction topologies.IEEE Trans Autom Control2005;50(5):655–61.

21.Wen JY,Kreutz-Delgado K.The attitude control problem.IEEE Trans Autom Control1991;36(10):1148–62.

22.Slotine JJ,Li W.Applied nonlinear control.Beijing:China Machine Press;2004,p.123–4.

23.Yao B,Tomizuka M.Adaptive robust control of SISO nonlinear systems in a semi-strict feedback form.Automatica1997;33(5):893–900.

25 March 2016;revised 6 June 2016;accepted 23 December 2016

Available online 16 February 2017

*Corresponding author.

E-mail addresses:sy1403105@buaa.edu.cn(R.Wang),ljk@buaa.edu.cn(J.Liu).

Peer review under responsibility of Editorial Committee of CJA.