REHMAN Abdur,WANG Qingwen

(1.College of Sciences,Shanghai University,Shanghai 200444,China; 2.University of Engineering&Technology Lahore,Lahore 54660,Pakistan)

Common least-squares solution to some matrix equations

REHMAN Abdur1,2,WANG Qingwen1

(1.College of Sciences,Shanghai University,Shanghai 200444,China; 2.University of Engineering&Technology Lahore,Lahore 54660,Pakistan)

Necessary and sufficient conditions are derived for some matrix equations that have a common least-squares solution.A general expression is provided when certain resolvable conditions are satisfied.This research extends existing work in the literature. Key words:matrix equation;least-squares solution;explicit solution;Moore-Penrose inverse;rank

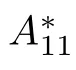
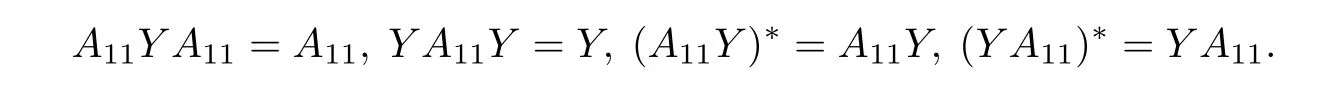
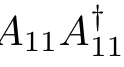
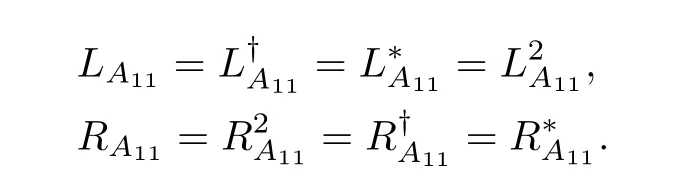
Linear matrix equations have been studied extensively in the matrix theory and its applications.For instance,

were investigated by Mitra[4]in 1973 over C.The system(1)was explored in[5-6]over a field.The solvability conditions of(1)over a principal domain was examined in[7].Wang[8]investigated(1)in 1996 over an arbitrary division ring.New necessary and sufficient conditions for the solvability of(1)are established.An expression of the general solution of(1)is also given when it is solvable[9].A symmetric and optimal approximate solution to(1)using an iterative technique was developed in[10].A common solution to(1)with a numerical algorithm was presented in[11].Consistency of(1)with an application was computed in[12]. Jones and Narathong also discussed(1)in[13].

When(1)is not solvable,one can find its approximate solution known as a least-squares solution.Least-squares solutions are often used in statistics.Conditions for the presence of a common least-squares solution to(1)were derived in[14].An exclusive expression for a common least-squares solution to(1)was also presented in[15].

Note that(1)is a particular case of

To our knowledge,common least-squares solution to(2)does not exist.Motivated by the afore-mentioned works,we present some necessary and sufficient conditions for(2)to have a common least-squares solution with an exclusive expression.

1 Preliminaries

This section gives some well-known results,that play a crucial role in the construction of the main result.

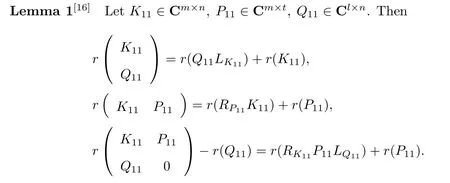
Lemma 2[14]Let A,B and C be known matrices over C of viable dimensions.Then

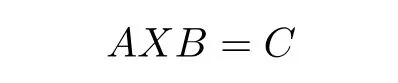
has a least-squares solution X if and only if the matrix equations

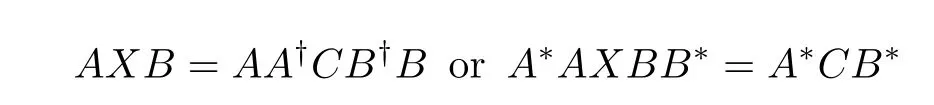
are consistent.With this condition,the general least-squares solution is

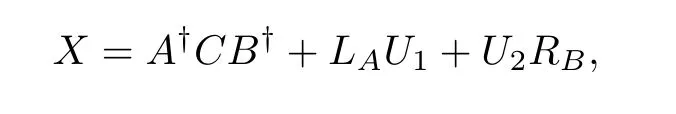
where U1and U2are free matrices of right dimensions.

Lemma 3[17]Let A1,B1,A2,B2and C be given matrices with possible dimensions. Set M=RA1A2,S=A2LMand N=B2LB1.Then the following conditions are identical.

(1)X1and X2have been solved by

(2)The rank equalities mentioned below are fulfilled:

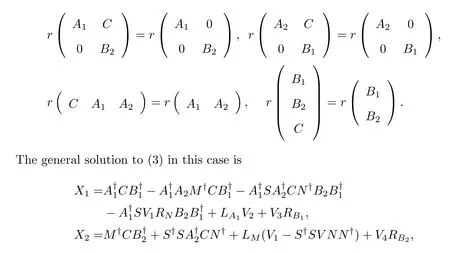
where V1,V2,V3,V4are free matrices over C of executable sizes.

2 Main results

This section presents conditions for a presence of the common least-squares solution to (2)with its exclusive expression.

Theorem 1Assume that A1,A2,A3,B2,B3,C1,C2and C3are given matrices of feasible shapes over C.Assign

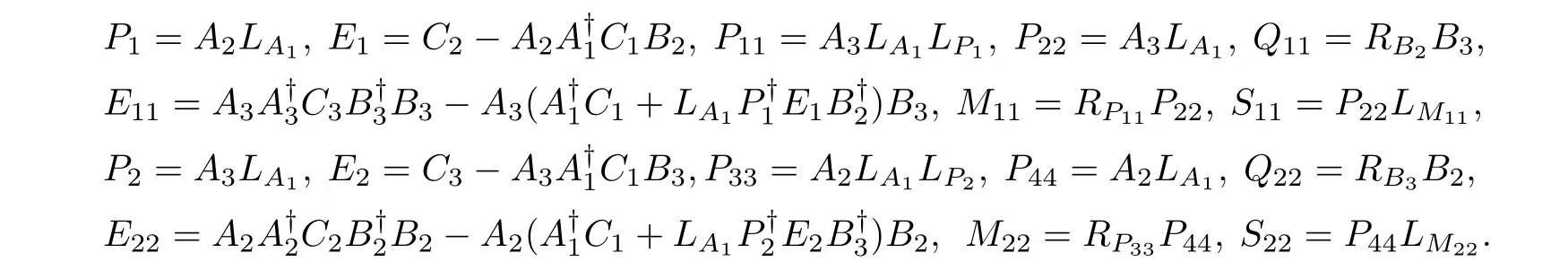
Then the matrix equations(2)have a common least-squares solution if and only if

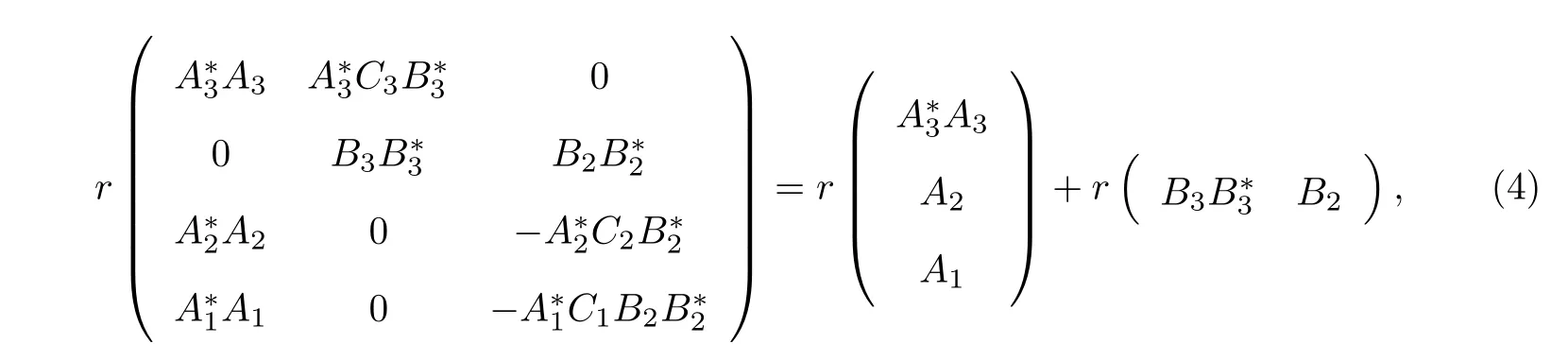
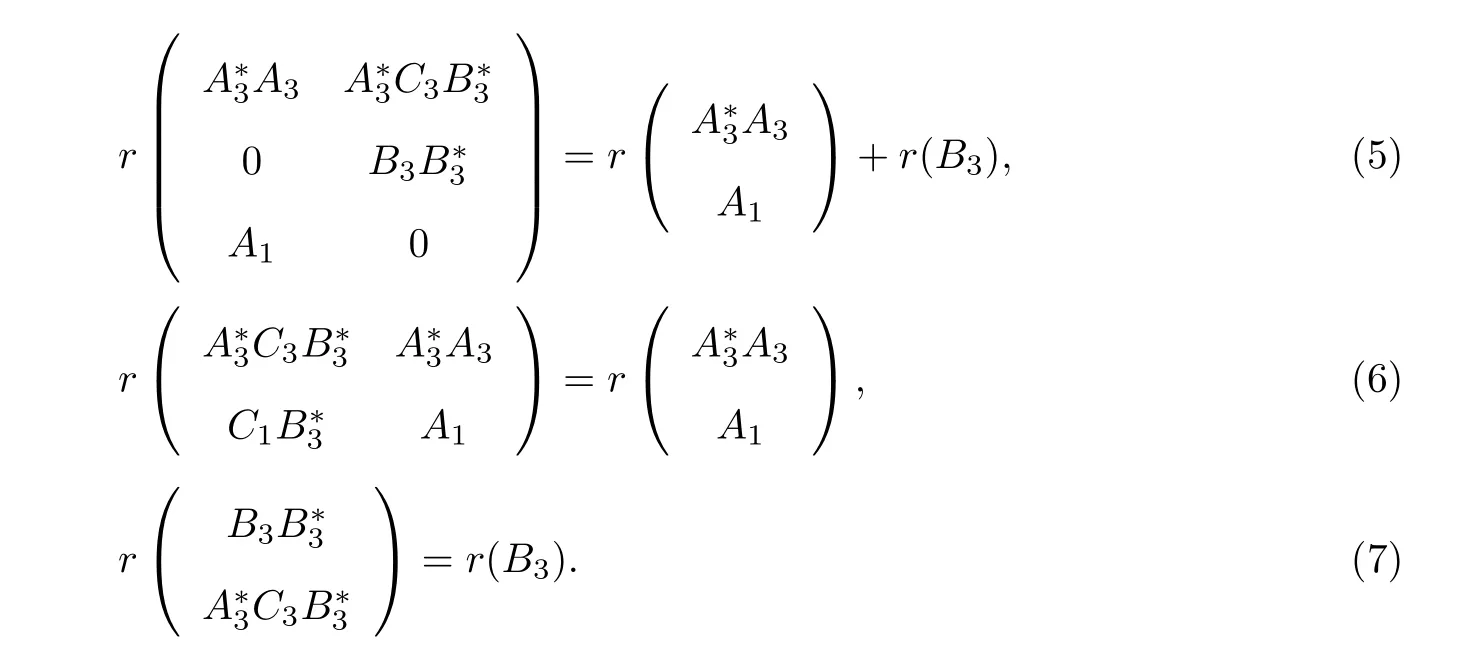
In this case,the general common least-squares solution to(2)is

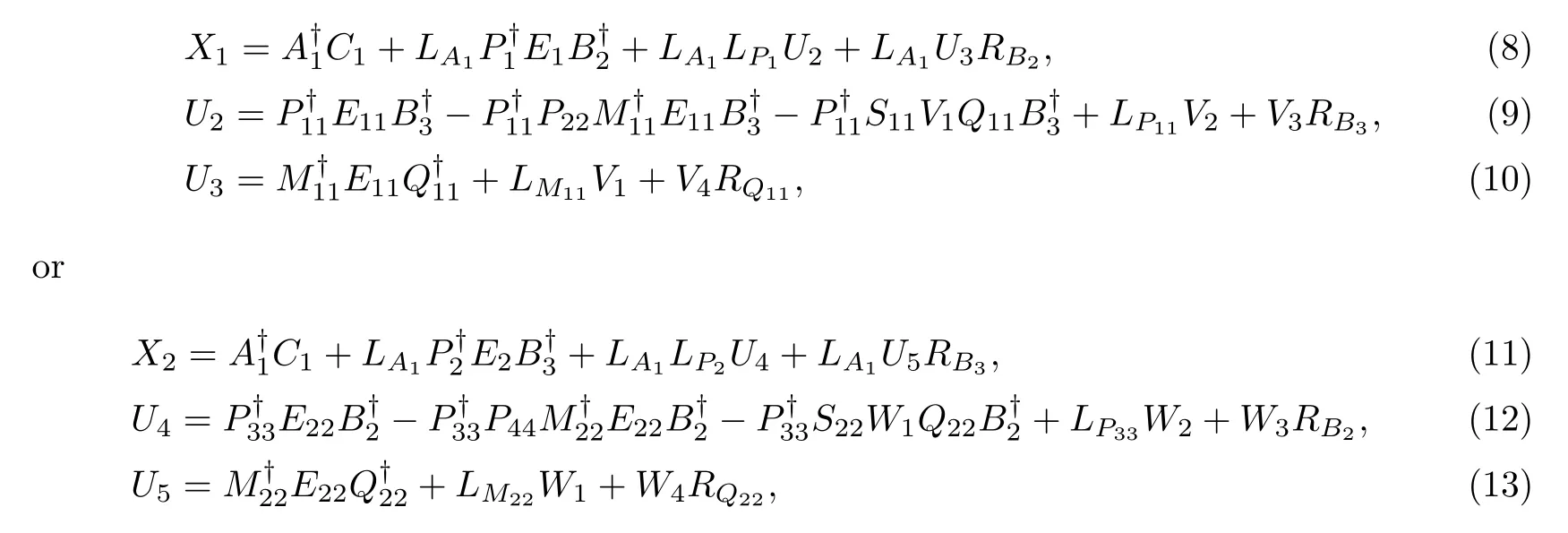
where V1,V2,V3,V4and W1,W2,W3,W4are free matrices of acceptable dimensions. ProofBy Lemma 2,the general least-squares solution to A1X=C1is

where U1is a free matrix of practical size. Using(14)in A2X1B2=C2,we have

Then by Lemma 2,the least-squares solution to(15)is

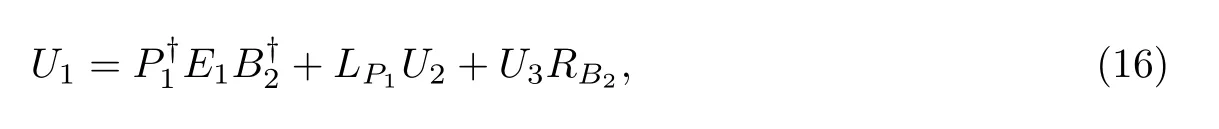
where U2and U3are free matrices of viable shapes. Using(16)in(14),we have

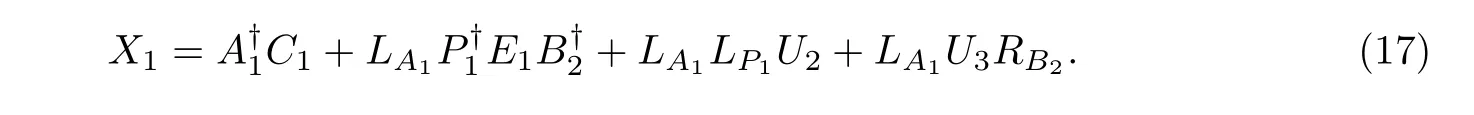
Substituting(17)in A3X1B3=C3,we obtain

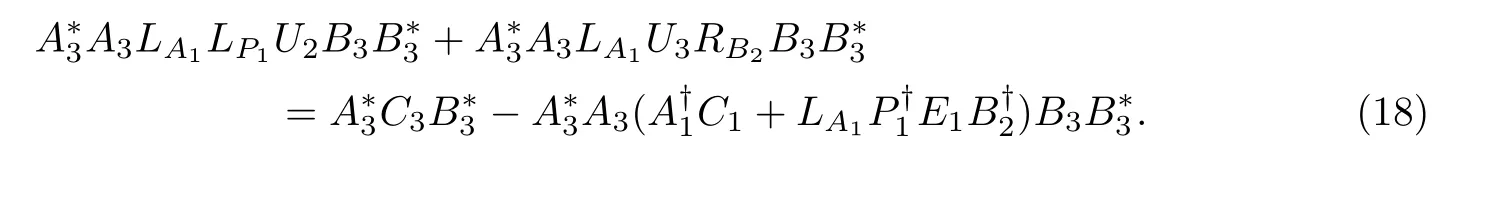
By Lemma 3,(18)is consistent if and only if

It is straightforward to show that(20)—(22)are equivalent to(5)—(7).We only show that (19)is equivalent to(14).

By Lemma 1,(19)is

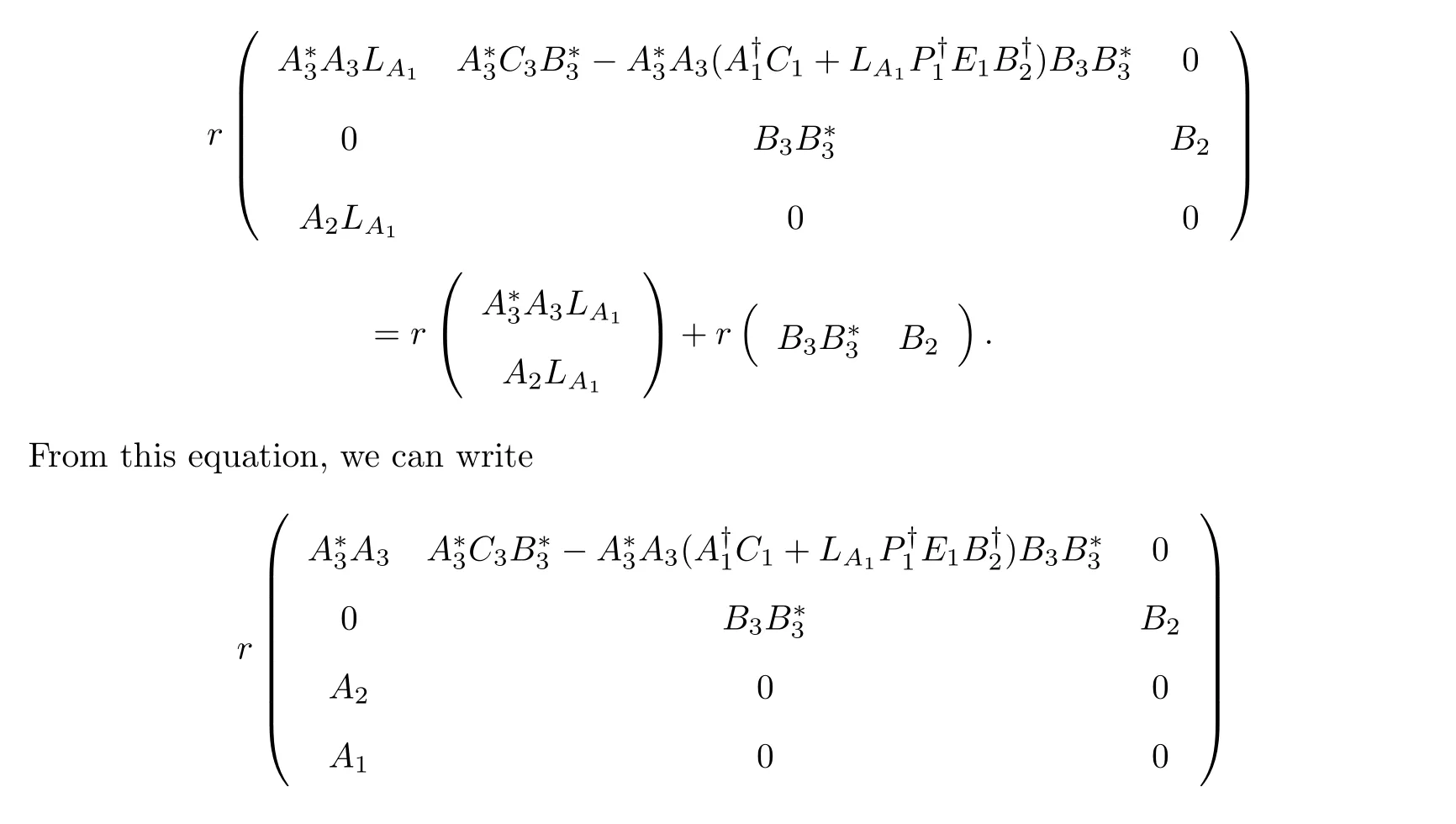
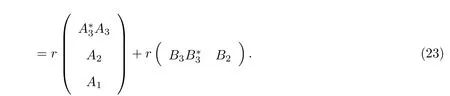
Now we evaluate the left-hand side of(23)by Lemma 1 and block elementary operations as follow:

Using(24)in(23),we get(4).

We observe that,(18)is similar to

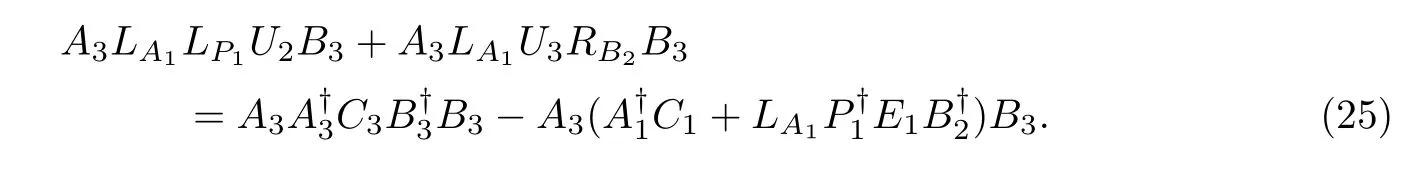
The general solution of(25)by Lemma 3 is

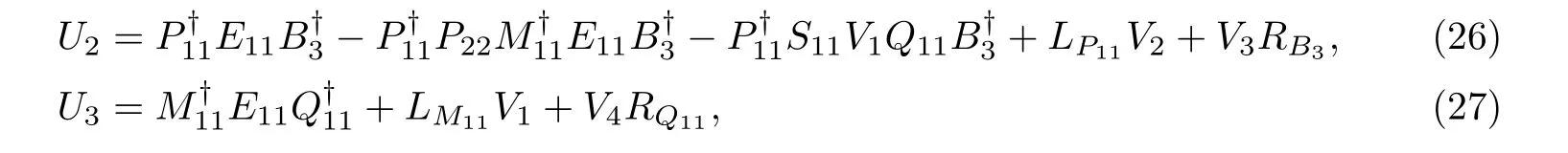
where V1,V2,V3,V4are free matrices of conformable dimensions.Combining(17),(26)and (27),we get(8)—(10).

Using the same technique,we can get(11)—(13).Thus,the theorem is proven.Obviously,representations of X1and X2are not the same.The sets{X1}and{X2}are equivalent because of(4)—(7).

Corollary 1Assume that the matrix equations in(2)are consistent,respectively. Assign

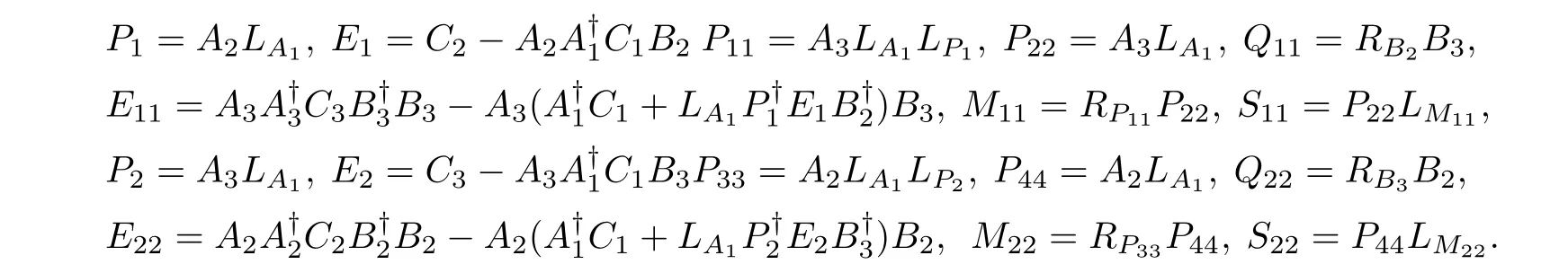
Then the matrix equations in(2)have a common solution if and only if

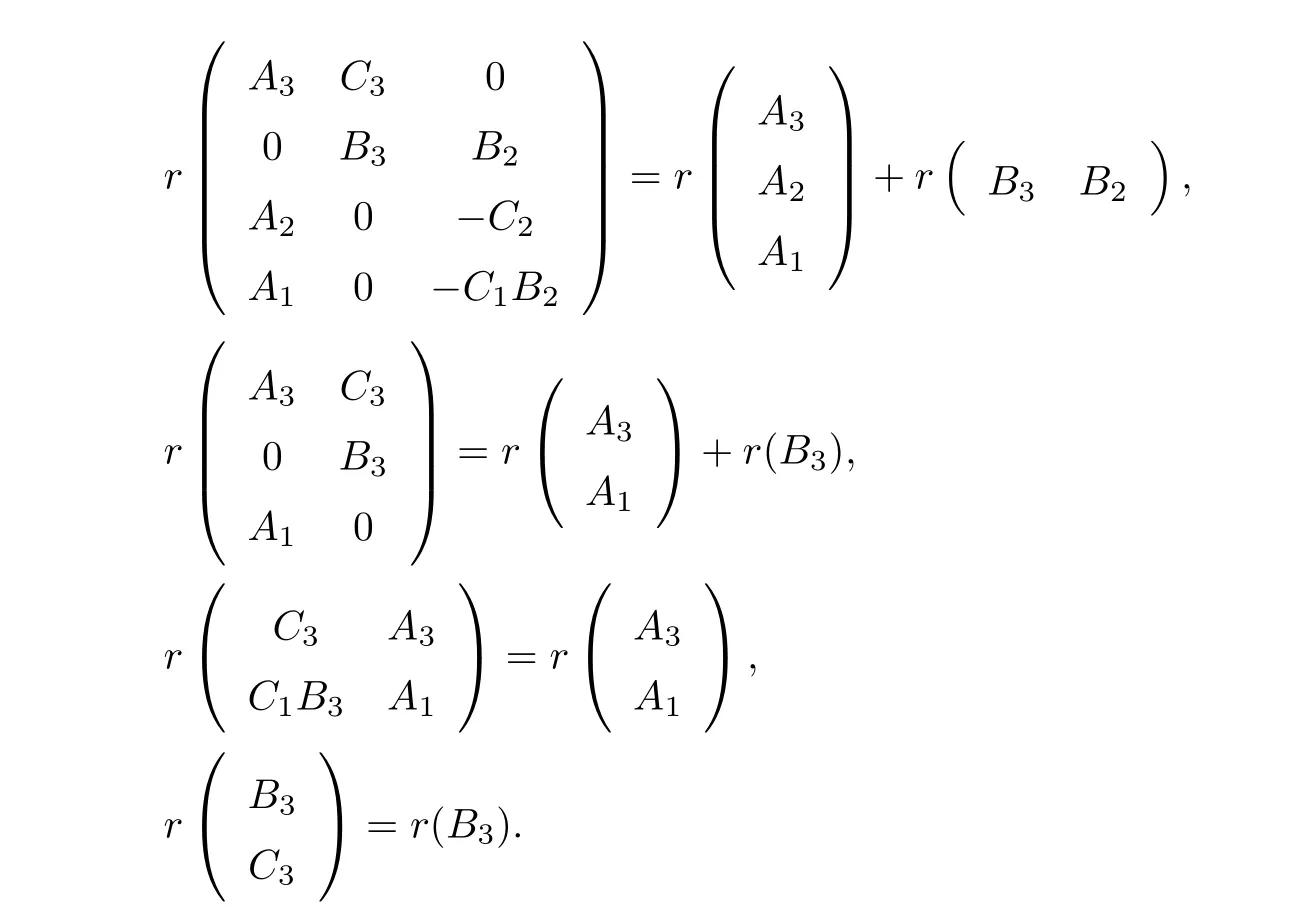
In this case,the general common solution to(2)is

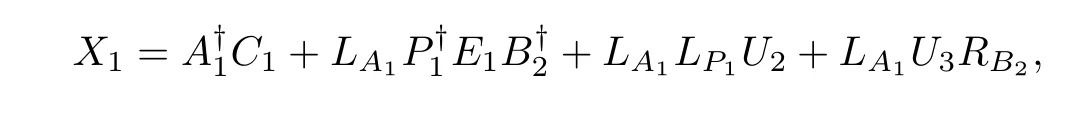
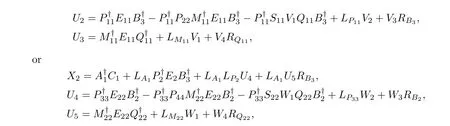
where V1,V2,V3,V4and W1,W2,W3,W4are arbitrary matrices of workable sizes.

When A1and C1in(2)are null matrices,we have the following corollary.

Corollary 2Assume that

Then the matrix equations(2)have a common least-squares solution if and only if

In this case,the general common least-squares solution to(1)is

where V1,V2,V3,V4and W1,W2,W3,W4are arbitrary matrices of adequate dimensions.

CommentCorollary 2 is the principal finding of[16].

3 Conclusion

We have derived an exclusive representation of the general common least-squares solution to(2)using generalized inverses and rank equalities when some necessary and sufficient conditions are fulfilled.

References:

[1]HUNGERFORD T W.Algebra[M].New York:Spring-Verlag,1980.

[2]BEN-ISRAEL A,GREVILLE T N E.Generalized inverses:theory and applications[M].New York: John Wiley&Sons,1974.

[3]CARADUS S R.Generalized inverses and operator theory[D].Kingston:Queen’s University,1978.

[4]MITRA S K.A pair of simultaneous linear matrix equations A1XB1=C1,A2XB2=C2and a matrix programming problem[J].Linear Algebra and Its Applications,1990,131(1):107-123.

[5]VAN DER WOUDE J W.Feedback decoupling and stabilization for linear system with multiple exogenous variables[D].Eindhoven:Technical University of Eindhoven,1987.

[6]VANDERWOULDEJ W.Almost noninteracting control by measurement feedback[J].Systems& Control Letters,1987,9(1):7-16.

[7]¨OZG¨ULER A B,AKAR N.A common solution to a pair of linear matrix equations over a principle domain[J].Linear Algebra and Its Applications,1991,144(15):85-99.

[8]WANG Q W.The decomposition of pairwise matrices and matrix equations over an arbitrary skew field[J].Acta Mathematica Sinica,1996,39(3):396-403.

[9]NAVARRA A,ODELL P L,YOUNG D M.A representation of the general common solution to the matrix equations A1XB1=C1and A2XB2=C2with applications[J].Computers& Mathematics with Applications,2001,41(7/8):929-935.

[10]PENG Y X,HU X Y,ZHANG L.An iterative method for symmetric solutions and optimal approximation solution of the systems of matrix equations A1XB1=C1,A2XB2=C2[J]. Applied Mathematics and Computation,2006,183(2):1127-1137.

[11]CHU K W E.Singular value and generalized singular value decompositions and the solution of linear matrix equations[J].Linear Algebra and Its Applications,1987,88:83-98.

[12]SHINOZAKI N,SIBUYA M.Consistency of a pair of matrix equations with an application[J].Keio Engineering Reports,1975,27(10):141-146.

[13]JONES J,JR NARATHONG C.Estimation of variance and covariance components in linear models containing multiparameter matrices[J].Mathematical and Computer Modelling,1988,11:1097-1100.

[14]LIU Y H.Ranks of least squares solutions of the matrix equation AXB=C[J].Computer& Mathematics Applications,2008,55(6):1270-1278.

[15]MARSAGLIA G,STYAN G P H.Equalities and inequalities for ranks of matrices[J].Linear and Multilinear Algebra,1974,2(3):269-292.

[16]LIU X F,YANG H.An expression of the general common least-squares solution to a pair of matrix equations with applications[J].Computers&Mathematics Applications,2011,61(10): 3071-3078.

[17]WANG Q W,VAN DER WOUDE J W,CHANG H X.A system of real quaternion matrix equations with applications[J].Linear Algebra and Its Applications,2009,431(12):2291-2303.

10.3969/j.issn.1007-2861.2015.02.012

1007-2861(2017)02-0267-09

Received:May 12,2015

WANG Qingwen,Professor,Ph.D.,E-mail:wqw369@yahoo.com

Chinese library classification:O 151.21Document code:A