Mei-Dan Chen(陳美丹),Xian Li(李咸),Yao Wang(王瑤),and Biao Li(李彪)

Ningbo Collaborative Innovation Center of Nonlinear Harzard System of Ocean and Atmosphere,and Department of Mathematics,Ningbo University,Ningbo 315211,China

1 Introduction

As we all know,with the development of science and technology in modern society,nonlinear evolution equations(NEEs)and their solutions play a major role in almost all the physics branches,such as fluid mechanics,[1]plasma physics,[2?3]optical fibers,[4?6]and so on.[7]Hence the explicit solutions of NEEs play a vital role in practical applications.Searching exact solutions of NEEs is one of the hot topics in nonlinear science.Various localized solutions such as solitons,[8?11]breathers[12]have been studied in the past few decades.

In soliton theory,[13?18]lump solutions have attracted more and more attention.[19?22]As a kind of rational function solutions,lump solutions localized in all directions in the space.Lump solutions can be studied based on the Hirota bilinear equations.For instance,a class of(2+1)-dimensional KPI equation,p-gBKP equation,KdV equation,CDGKS equation,and Ito equation have been obtained by using its Hirota bilinear form.[23?27]More importantly,it will happen collision among different solitons.There are two kinds of collision,either the elastic or the inelastic.It is reported that lump solutions will keep their shapes,amplitudes,velocities after the collision with soliton solutions,which means the collision is completely elastic.[28]While many other collisions are completely inelastic.[29?30]On the basis of different conditions,the collision will change essentially.

In this paper,we consider a(3+1)-dimensional nonlinear evolution equation(NEE)

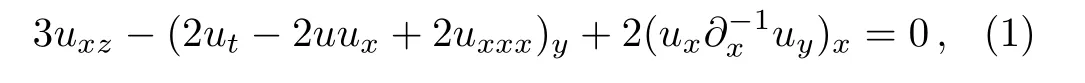
which was first introduced in the study of the algebraic geometrical solutions.[32]Though it is not clear about the application of this(3+1)-dimensional mode for physics or other sciences,it is not hard to find that the relationship between the(3+1)-dimensional equation and these sciences.In 2015,Wazwaz proposed the multiple soliton solution of this equation.Recently,Shi et al.have studied the rouge wave of this equation.[31]As far as we know,lump solutions and some interaction solutions of this equation have not been studied.

In our present work,we would like to focus on the lump solutions and some interaction solutions to Eq.(1).First,we give the Hirota bilinear form of Eq.(1)and search for quadratic function solutions to the corresponding(3+1)-dimensional bilinear NNE equation,and then derive lump solutions with the symbolic computation.Second,we present interaction solutions of lump solutions with one stripe soliton by combining positive quadratic function with exponential function.Third,we obtain a pair of resonance stripe solitons interacting with lump solutions by combining hyperbolic cosine function with the positive quadratic function.And the dynamic properties of these solutions are shown by some figures under some special parameters.Finally,a sort of conclusion will be given at the end of the paper.

2 Lump Solutions to(3+1)-D NEE Equation

Bell polynomial theories motivate us to consider a dependent variable transformation,

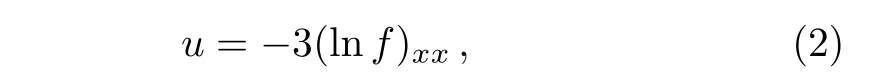
substituting Eq.(2)into Eq.(1),we obtain the following Hirota bilinear form:

herefis a real function with respect to variablex,y,z,andt,and the derivativesDtDy,Dy,andDzDxare the Hitota bilinear operates.Whenz=x,Eq.(3)becomes the following formula

Therefore,iffsolves the bilinear Eq.(4),thenu=?3(lnf)xxwill solve Eq.(1).To seek lump solutions of this equation,we make the following assumption:

whereai,1≤i≤9,are real parameters to be determined.We obtain a polynomial of the variablesx,y,zandtby substituting Eq.(5)into Eq.(4)and eliminate the coeffi-cients of the polynomial aboutaiand with via symbolic computation.We obtain the following special solutions:

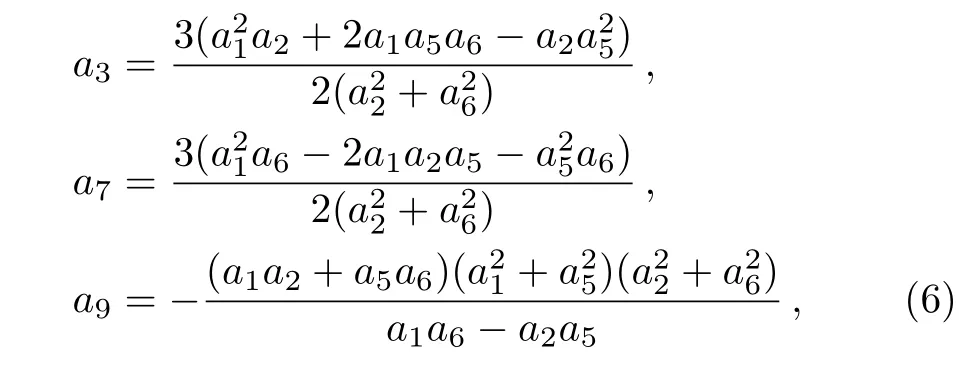
which need to satisfy determinant conditions

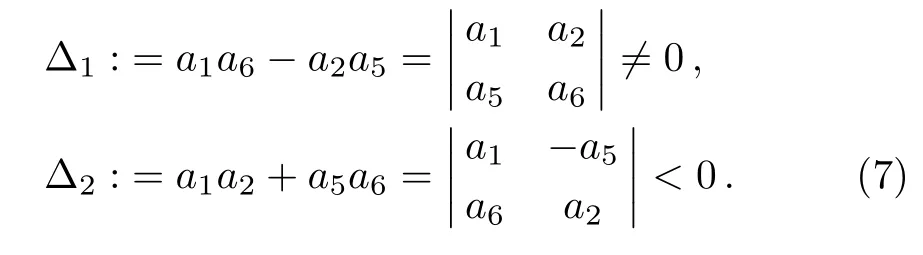
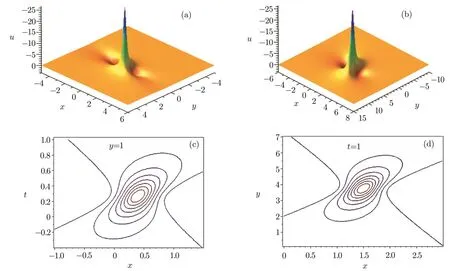
Fig.1 (Color online)A lump solution u of Eq.(1)in(x,t)-plane(a)and(x,y)-plane(b)with the parameters(10).

These sets lead to guarantee the well-defined off,and a class of positive quadratic function solutions to the bilinear in Eq.(4):

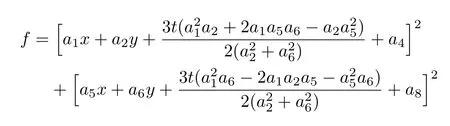
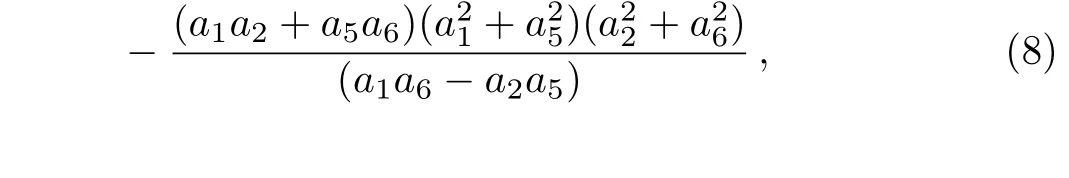
then the solution ofucan be written

where

In a class of lumps,a1,a2,a4,a5,a6,anda8are provided arbitrarily that the solutions are well defined.That is to say,if the determinant conditions of Eq.(7)are satisifed,then positive quadratic function solutions and lump solutions with special values of the parameters are given as follows.The conditions Eq.(7)also leads to+/=0,and soa9＞0.And the conditions also guarantee both analyticity and localization of the solutions in Eq.(9).

and their plots wheny=1 andt=1 are depicted in Fig.1,respectively.

Here we choose the parametersa4=0,a8=0,which imply each lump is centered at the origin whent=0.As shown in both Figs.1(a)and 1(b),the amplitudes of the lump are 27,which can be calculated precisely by the formula Eq.(9).Figures 1(c)and 1(d)show contour plot of the lump solutions aty=1 andt=1,respectively.

3 Interaction Solutions between Lump Solutions and One Stripe Soliton

In this section,we apply quadratic function adding with exponential function to study the interaction solution between the lump solution and one stripe soliton.Makefas a positive quadratic function add with exponential function,that is

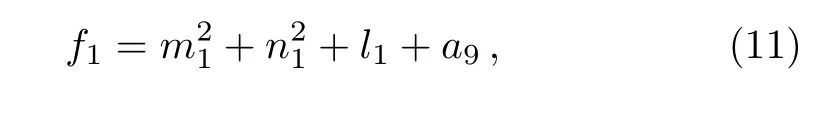
where

which needs to satisfy the following determined conditions

Fig.2 (Color online)The interaction of a lump and as oliton solution u of Eq.(1)in(x,y)-plane with the parameters(14).

Based on the transformationu=?3(lnf1)xx,the solution of Eq.(4)will be obtained 1

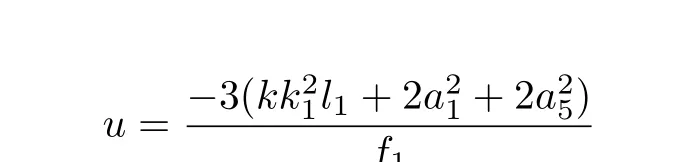
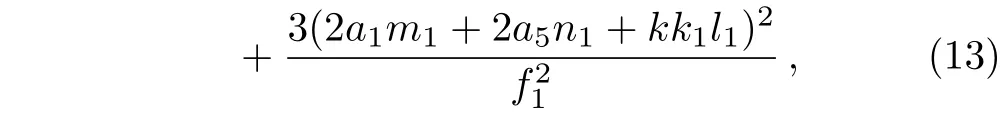
where

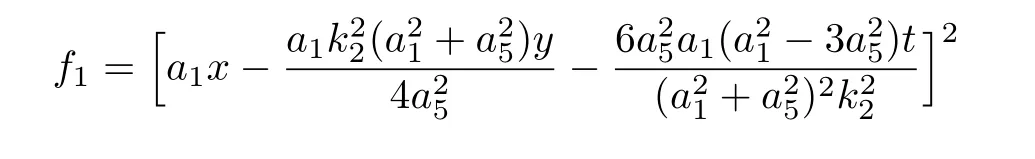
By choosing appropriate values of these parameters,we set

Figure 2 shows the dynamic graphs of interaction between the lump solutions and one stripe soliton.There are one lump and one stripe soliton propagates in the space in Fig.2(a).Whent=0,the lump to tangle with the stripe as in Fig.2(b).Then lump begins to be swallowed by stripe soliton step by step as shown in Figs.2(c)and 2(d),and its energy begins to transfer into the stripe soliton gradually,until these two kinds of solitons blend into one soliton and continue to spread.

4 Interaction Solutions between Lump Solutions and a Pair of Resonance Stripe Solitons

Based on the collision of lump solutions and one stripe soliton,we begin to discuss the collision of lump solutions and a pair of stripe solitons,set:

where

Once again,substituting Eq.(16)into Eq.(4),with a complex symbolic calculation,the relations of these parameters are

which need to satisfy

Then,with the transformationu=?3(lnf2)xx,we can obtain the solutionuas follows:

According to the expression off2,m2,n2,asymptotic property of lump solutions and a pair of resonance solitons are analyzed.Take

comparedξ1,ξ2,ξ3with each other,it can be proved

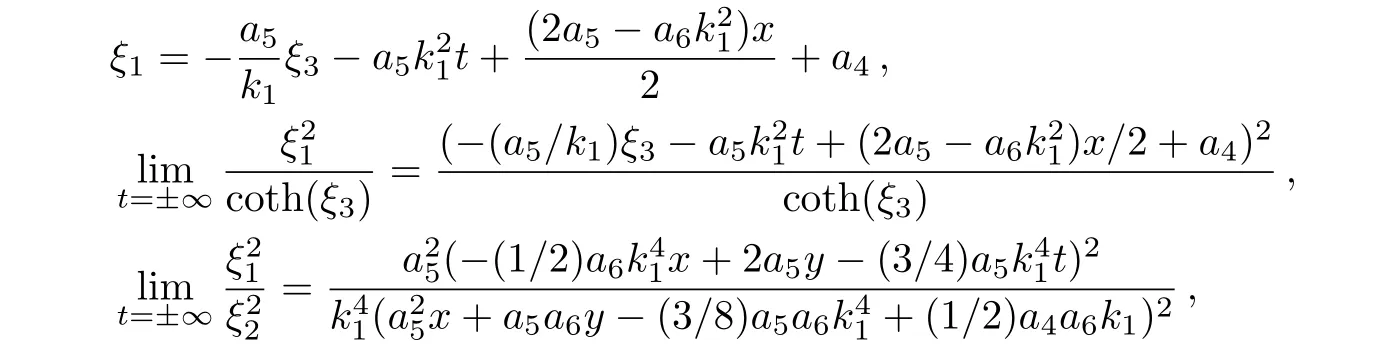
ξ1,ξ2are same order due tot= ±∞.We only need to compareξ21,cosh(ξ3).Supposeξ3is a constant thatξ1is a combination of scale change and time displacement forξ3.Whent=±∞,we can obtain a conclusion,only a pair of resonance solitons exist.Whentup to zero,lump solutions property is more obvious,which is shown in Fig.3.We choose a special instance of the parameters:

A pair of resonance solitons evolveing in the(x,y)-plane,and lump is almost invisible as shown in Fig.3(a).Lump propagates and to tangle with one of stripe solitons as in Fig.3(b).An interaction between lump solutions and resonance solitons in Fig.3(c),and lump becomes more vigorous.At a special time,amplitude of lump will be up to the maximum.Figures 3(c)and 3(d)show lump begins to be swallowed by other stripe solitons step by step,until lump blend into stripe solitons and continue to spread.

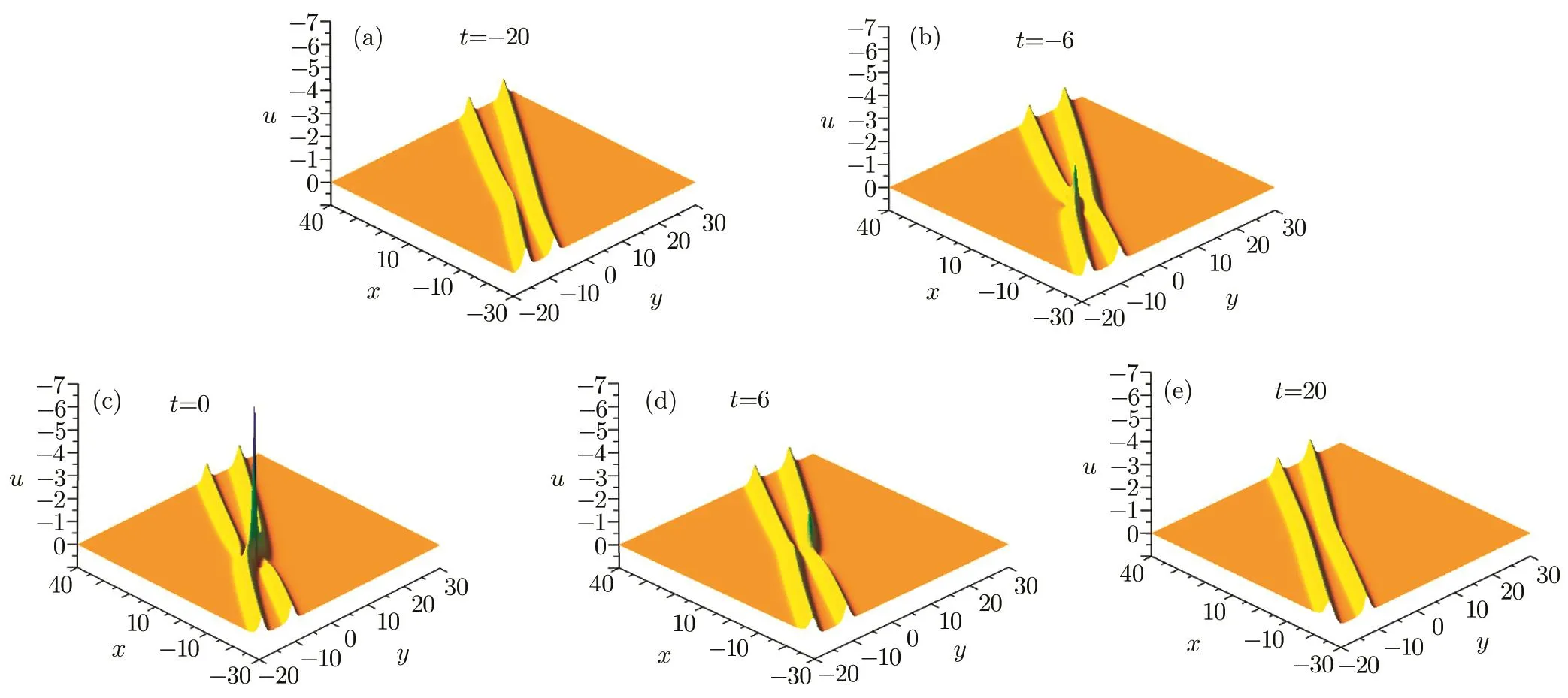
Fig.3 (Color online)The interaction of a lump and a pair of solitons solution u of Eq.(1)in(x,y)-plane with the parameters(19).

5 Conclusion

In summary,based on the Hirota bilinear form of Eq.(1)and symbolic computation,a class of lump solutions and some interaction solutions are derived.We have searched for quadratic function from the Hirota bilinear form of Eq.(1)and then derived lumps at first.And the quadratic function contain six free parameters,four of which satisfy two determinant conditions so as to insure analyticity and rational localization of the solutions,while the others are free.The dynamic properties of the interaction solutions are shown in Fig.1.Then,by combining positive quadratic function with exponential function,the interaction solutions between lump solutions and the stripe solution are derived under some conditions.The dynamic properties of the interaction solutions as shown in Fig.2.From which we can see that there are one lump and one stripe soliton evolving in the space,as times go on,the lump to tangle with stripe soliton and begin to be swallowed by stripe soliton step by step,until these two kinds of solitons blend into one soliton and continue to spread.In Sec.4,we extend this method to combination of positive quadratic function and hyperbolic cosine function.The interaction solutions between lump solutions and a pair of resonance stripe solitons are presented by this way,and asymptotic property of the interaction solutions are analyzed under some specific conditions.From Fig.3, firstly a pair of resonance solitons evolute in the(x,y)-plane and lump is almost invisible,and then lump tangles with one of the a pair of stripe solitons.In this process amplitude of lump reached the maximum value.As time goes by,lump beginning to be swallowed by the other stripe soliton step by step,until lump blend into stripe solitons and continue to spread.The method can also be extended to other types of nonlinear evolution equations in mathematical physics.

References

[1]A.N.Ganshin,V.B.E fimov,L.P.Mezhov-Deglin,and P.V.McClintock,Phys.Rev.Lett.101(2008)265303.

[2]W.M.Moslem,Phys.Plasmas.18(2011)032301.

[3]H.Bailung,S.K.Sharma,and Y.Nakamura,Phys.Rev.Lett.107(2011)255005.

[4]C.Kharif,E.Pelinovsky,and A.Slunyaev,Rogue Waves in the Ocean,Springer,Berlin(2009).

[5]D.R.Sollim,C.Ropers,P.Koonath,and B.Jalali,Nature(London)450(2007)1054.

[6]B.Kibler,J.Fatome,C.Finot,et al.,Nat.Phys.6(2010)790.

[7]Z.Y.Yan,Commun.Theor.Phys.54(2010)947.

[8]M.J.Ablowitz and P.A.Clarkson,Solitons,Nonlinear Evolution Equations and Inverse Scattering,Cambridge University Press,Oxford(1991).

[9]H.Triki,B.J.M.Sturdevant,T.Hayat,O.M.Aldossary,and A.Biswas,Can.J.Phys.89(2011)979.

[10]X.Lü and M.Peng,Chaos.23(2013)013122.

[11]A.H.Bhrawy,M.A.Abdelkawy,and A.Biswas,Indian J.Phys.87(2013)1125.

[12]S.Y.Lou,Phys.Scr.65(2002)7.

[13]A.M.Wazwaz and G.Q.Xu,Commun.Theor.Phys.63(2015)727.

[14]W.G.Cheng,B.Li,and Y.Chen,Commun.Theor.Phys.63(2015)549.

[15]S.Michelle,A.A.Alshaery,E.M.HIlal,A.H.Bhrawy,Q.Zhou,and A.Biswas,Optolectron.Adv.Mater.9(2015)14.

[16]J.V.Guzman,E.M.Hilal,et al.,Proc.Rom.Acad.Ser.A 16(2015)41.

[17]D.S.Wang,S.Yin,and Y.F.Liu,Appl.Math.Comput.229(2014)296.

[18]X.Lü,W.X.Ma,J.Yu,F.H.Lin,and C.M.Khalique,Nonlinear Dyn.82(2015)1211.

[19]W.X.Ma,Z.Y.Qin,and X.Lü,Nonlinear Dyn.84(2016)923.

[20]W.X.Ma,Phys.Lett.A 379(2015)1975.

[21]D.J.Kaup,J.Math.Phys.22(1981)1176.

[22]K.Imai,Prog.Theor.Phys.98(1997)1013.

[23]Q.L.Zha,Phys.Lett.A 377(2013)3012.

[24]H.C.Ma and A.P.Deng,Commun.Theor.Phys.65(2016)546.

[25]X.Zhang,Y.Chen,and X.Y.Tang,preprint arXiv:1610.09507[nlin.SI](2016).

[26]C.J.Wang,Nonlinear Dyn.84(2016)697.

[27]Y.N.Tang,S.Q.Tao,and Q.Guan,Comp.Math.Appl.72(2016)2334.

[28]A.S.Fokas,D.E.Pelinovsky,and C.Sulem,Physica D 152(2001)189.

[29]C.Becker,K.Sengstock,P.Schmelcher,P.G.Kevrekidis,and R.C.Gonz′alez,New J.Phys.15(2013)113028.

[30]W.Tan and Z.D.Dai,Nonlinear Dyn.85(2016)817.

[31]Y.B.Shi and Z.Yi,Commun.Nonlinear Sci.Numer.Simulat.44(2017)120.

[32]Z.J.Zhou,J.Z.Fu,and Z.B.Li,Appl.Math.Comput.217(2010)92.